Úvod do odhadu pohybu s optickým tokem

v tomto tutoriálu se ponoříme do základů optického toku, podíváme se na některé jeho aplikace a implementujeme jeho dvě hlavní varianty (řídké a husté). Krátce také diskutujeme o novějších přístupech využívajících hluboké učení a slibné budoucí směry.

Nedávné objevy v počítačovém vidění výzkum umožnily stroje vnímat okolní svět prostřednictvím techniky jako objekt detekce pro detekci instance objektů, které patří do určité třídy a sémantické segmentace pro pixel-moudrý klasifikace.

pro zpracování video vstupu v reálném čase však většina implementací těchto technik řeší pouze vztahy objektů ve stejném rámci \((x, y)\) bez ohledu na časové informace \((t)\). Jinými slovy, přehodnocují každý snímek nezávisle, jako by se jednalo o zcela nesouvisející obrázky, pro každý běh. Nicméně, co když potřebujeme vztahy mezi po sobě jdoucích snímků, například, chceme, aby se sledování pohybu vozidel přes rámy odhadnout jeho aktuální rychlost a předvídat jeho pozici v dalším snímku?

Nebo, alternativně, co když budeme požadovat informace o lidských představují vztahy mezi po sobě jdoucích snímků, rozpoznat lidskou činností jako lukostřelba, baseball a basketbal?

V tomto tutoriálu jsme se naučit, co Optického Toku je, jak realizovat své dvě hlavní varianty (řídké a husté), a také získat velký obraz z novějších přístupů zahrnující hluboké učení a perspektivní budoucí směry.

Co je optický tok?
Prováděcí Řídký Optický Tok
Prováděcí Hustý Optický Tok
Hluboké učení a mimo

Co je to optický tok?

začněme s porozuměním optického toku na vysoké úrovni. Optický tok je pohyb objektů mezi po sobě jdoucími snímky sekvence, způsobený relativním pohybem mezi objektem a kamerou. Problém optického toku může být vyjádřen jako:

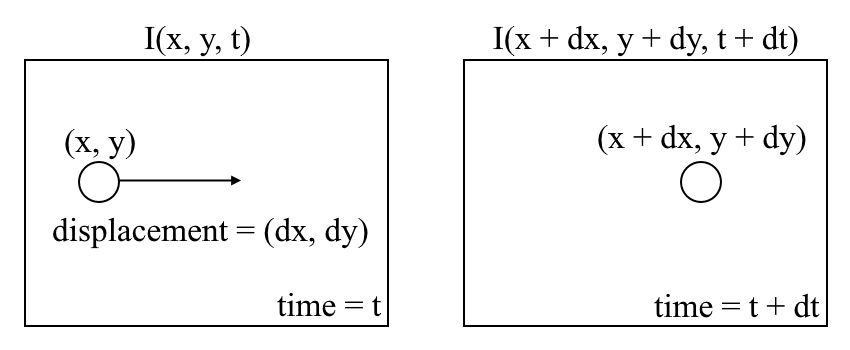
kde mezi po sobě jdoucích snímků, můžeme vyjádřit obraz intenzity \((I)\) jako funkci prostoru \((x, y)\) a \(v(t)\). Jinými slovy, pokud vezmeme první obrázek \(I (x, y, t)\) a přesuneme jeho pixely o \((dx, dy)\) přes \(t\) čas, získáme nový obrázek \(I(x + dx, y + dy, t + dt)\).

nejprve předpokládáme, že intenzity Pixelů objektu jsou konstantní mezi po sobě jdoucími snímky.

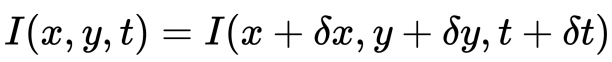
za Druhé, vezmeme Taylor Série Sbližování právních RHS a odstranění běžných podmínek.

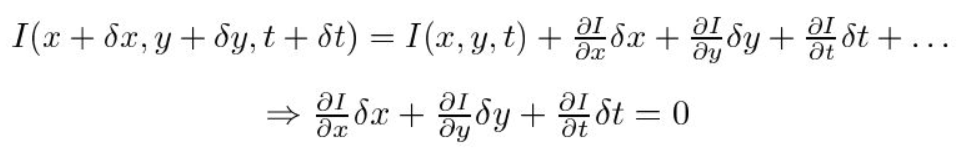
za Třetí, vydělíme \(dt\) k odvození rovnice optického toku:

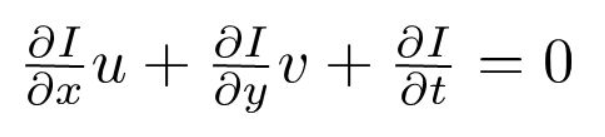
, kde \(u = dx/dt\) a \(v = dy/dt\).

\(dI / dx, dI / dy\) a \(dI / dt\) jsou obrazové přechody podél vodorovné osy, svislé osy a času. Proto končíme problémem optického toku, tedy řešením \(u (dx/dt)\) a \(v (dy/dt)\) pro určení pohybu v čase. Můžete si všimnout, že nemůžeme přímo vyřešit rovnici optického toku pro \(u\) a \(v\), protože existuje pouze jedna rovnice pro dvě neznámé proměnné. K řešení tohoto problému implementujeme některé metody, jako je metoda Lucas-Kanade.

Řídké vs Hustý Optický Tok

Sparse optical flow dává tok vektorů některých „zajímavých funkcí“ (řekněme pár pixelů zobrazující hrany nebo rohy objektu) v rámci, zatímco Hustý optický tok, který dává tok vektorů celý rám (všechny pixely) – až na jeden tok vektoru na pixel. Jak byste uhodli, hustý optický tok má vyšší přesnost za cenu pomalého / výpočetně nákladného.

Prováděcí Řídký Optický Tok

Řídký optický tok vybere řídké sadu funkcí pixelů (např. zajímavé funkce, jako jsou hrany a rohy) sledovat své vektorů rychlosti (pohybu). Extrahované funkce jsou předávány ve funkci optického toku z rámu do rámu, aby se zajistilo sledování stejných bodů. Existují různé implementace řídký optický tok, včetně Lucas–Kanade metoda Horn–Schunck metoda, Buxton–Buxton metoda, a další. Pro implementaci budeme používat metodu Lucas-Kanade s OpenCV, open source knihovnou algoritmů počítačového vidění.

Nastavení prostředí

Pokud nemáte již OpenCV nainstalován, otevřete Terminál a spusťte:

pip install opencv-python

Nyní, clone tutorial repozitáře příkazem:

git clone https://github.com/chuanenlin/optical-flow.git

Next, otevřít sparse-starter.py pomocí textového editoru. Budeme psát celý kód v tomto souboru Pythonu.

Konfigurace OpenCV číst video a nastavení parametrů

Shi-Tomasi Rohový Detektor – výběr pixelů pro sledování

Pro zavedení sparse optical flow, máme jen sledovat pohyb sadu funkcí pixelů. Funkce v obrazech jsou body zájmu, které představují bohaté informace o obsahu obrazu. Takovými rysy mohou být například body v obraze, které jsou invariantní k překladu, měřítku, rotaci a změnám intenzity, jako jsou rohy.

Shi-Tomasi Rohový Detektor je velmi podobný populární Harris Corner Detector, které mohou být realizovány následující tři postupy:

1. Určit windows (malý obrázek záplaty) s velkými gradienty (rozdíly v obrazu intenzity) při překladu v obou \(x\) a \(y\) směry.
2. pro každé okno Vypočítejte skóre \(R\).
3. v závislosti na hodnotě \(R\) je každé okno klasifikováno jako plochý, okraj nebo roh.

Pokud byste se chtěli dozvědět více o podrobném matematickém vysvětlení detektoru Harris Corner, neváhejte projít těmito snímky.

Shi a Tomasi později provedli malou, ale účinnou úpravu detektoru Harris Corner v jejich papírových dobrých funkcích pro sledování.

modifikací je rovnice, ve které se vypočítává skóre \(R\). V detektoru Harris Corner je bodovací funkce dána:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{stopy} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{stopy} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

Místo toho, Shi-Tomasi navrhl skórovací funkce jako:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

což v podstatě znamená, že pokud \(R\) je větší než práh, je klasifikován jako roh. Následující porovnává bodovací funkce Harris (vlevo) a Shi-Tomasi (vpravo) v \(λ1-λ2\) prostoru.

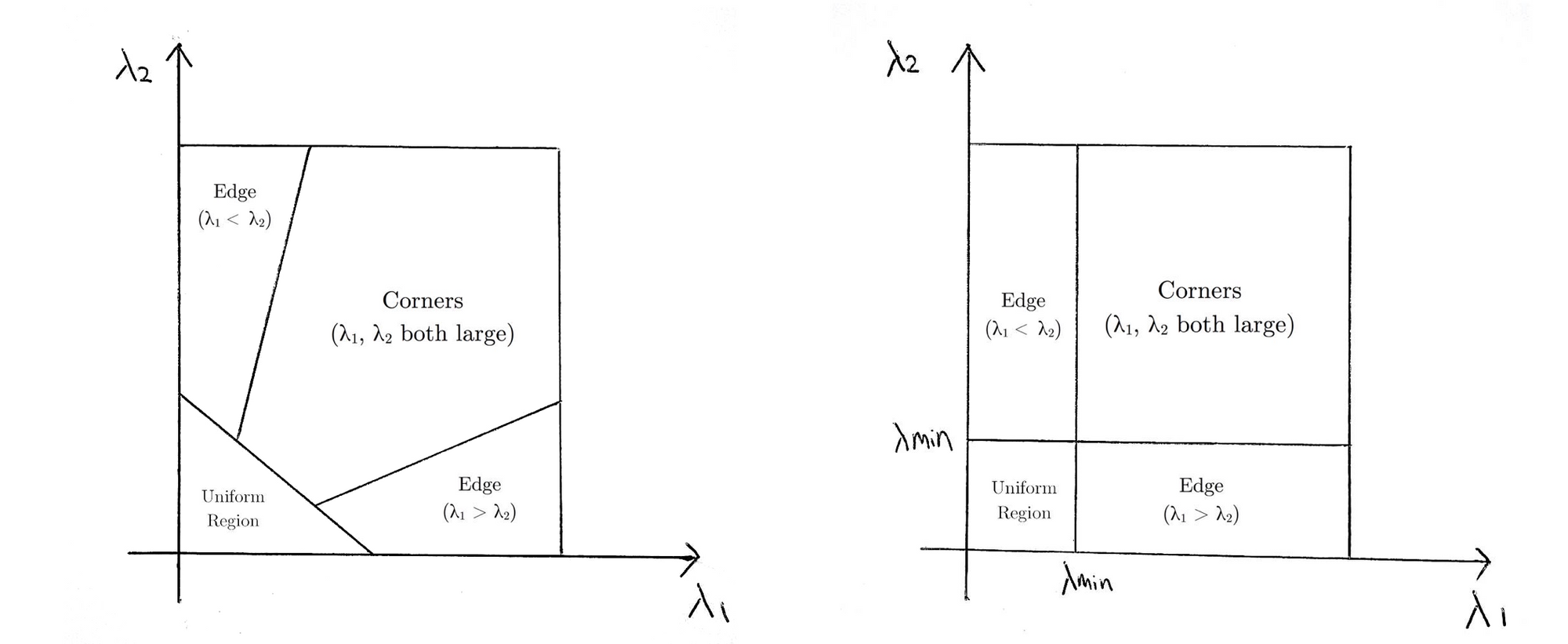
pro Shi-Tomasi, pouze pokud \(λ1\) a \(λ2\) jsou nad minimálním prahem \(λmin\) je okno klasifikováno jako roh.

dokumentaci OpenCV implementace Shi-Tomasi pomocí goodFeaturesToTrack() naleznete zde.

Sledování Konkrétních Objektů

může být scénáře, kde chcete sledovat pouze konkrétní objekt zájmu (řekněme sledování určité osoby), nebo jeden kategorie objektů (stejně jako všechny 2 kolář-vozidla v provozu). Kód můžete snadno upravit tak, aby sledoval pixely požadovaných objektů změnou proměnné prev.

můžete také kombinovat detekci objektů s touto metodou pouze odhadnout tok pixelů v detekovaných ohraničujících rámečcích. Tímto způsobem můžete ve videu sledovat všechny objekty určitého typu/kategorie.

Lucas-Kanade: Řídký Optický Tok

Lucas a Kanade navrhla efektivní technika pro odhad pohybu zajímavých funkcí porovnáním dvou po sobě jdoucích snímků v jejich papíru, Opakující se Obraz Registrační Technika s Aplikace pro Stereo Vidění. Metoda Lucas-Kanade funguje za následujících předpokladů:

1. Dva po sobě jdoucí snímky jsou odděleny malý přírůstek času (\(dt\)) tak, že objekty nejsou vysídlených výrazně (jinými slovy, metoda funguje nejlépe s pomalu se pohybujících objektů).
2. rámeček zobrazuje“ přirozenou “ scénu s texturovanými objekty vykazujícími odstíny šedé, které se plynule mění.

Za prvé, za těchto předpokladů můžeme vzít malé okno 3×3 (sousedství) kolem funkcí detekovaných Shi-Tomasi a předpokládat, že všech devět bodů má stejný pohyb.

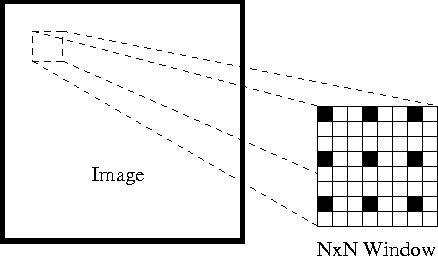
To může být reprezentován jako

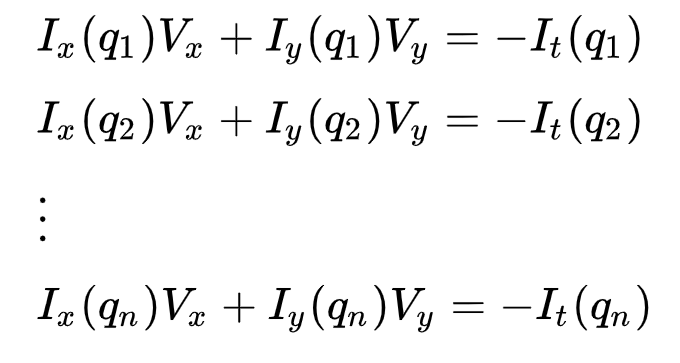
, kde \(q_1, q_2, …, q_n\) značí pixelů uvnitř okna (např. \(n\) = 9 pro 3×3 okno) a \(I_x(q_i)\), \(I_y(q_i)\) a \(I_t(q_i)\) značí parciální derivace obrazu \(I\) s ohledem na pozici \((x, y)\) a \(t\), pro pixel \(q_i\) v současné době.

Toto je pouze rovnice optického toku (kterou jsme popsali dříve) pro každý z n Pixelů.

sada rovnic mohou být zastoupeny v maticové formě, kde \(Av = b\):

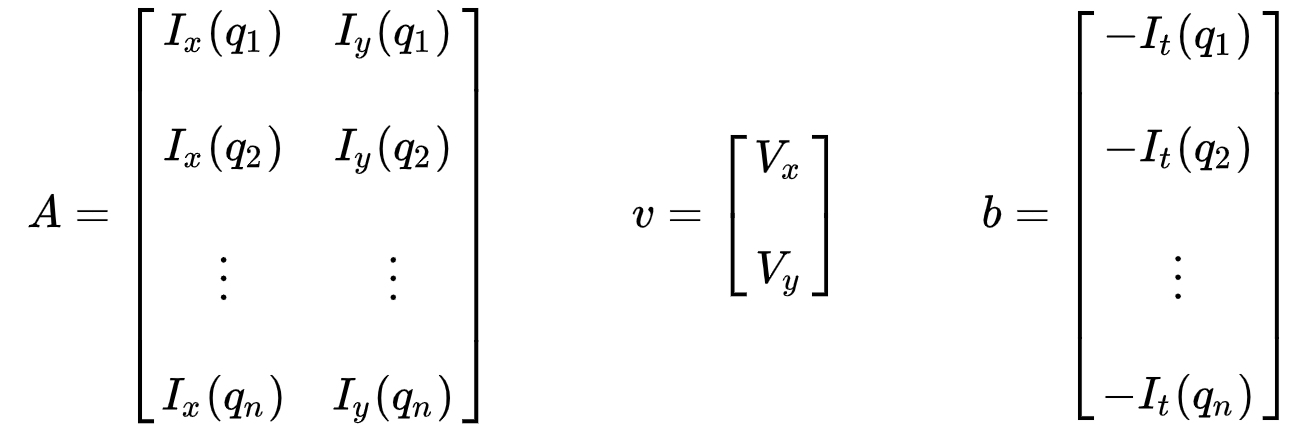
Vezměte na vědomí, že dříve (viz „Co je to optický tok?“sekce), čelili jsme problému, že musíme vyřešit dvě neznámé proměnné jednou rovnicí. Nyní čelíme nutnosti řešit dvě neznámé (\(v_x\) a \(V_y\)) s devíti rovnicemi, které jsou nadměrně určeny.

za Druhé, řešit přes-rozhodnuty problém, můžeme použít nejmenších čtverců přiléhající k získání následující dvě rovnice-dvě neznámé problém:

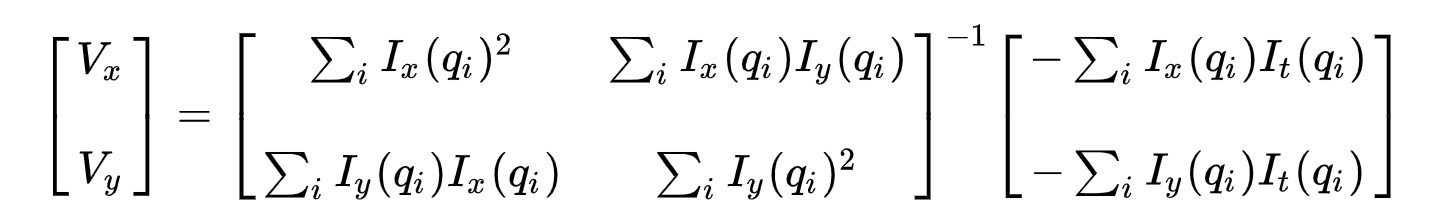
, kde \(Vx = u = dx/dt\) značí pohyb \(x\) v průběhu času a \(Vy = v = dy/dt\) označuje pohyb y v průběhu času. Řešení pro dvě proměnné dokončí problém optického toku.

stručně řečeno, jsme se identifikovat některé zajímavé funkce pro sledování a iterativně, výpočet optického toku vektory těchto bodů. Přijetí metody Lucas-Kanade však funguje pouze pro malé pohyby (z našeho původního předpokladu) a selže, když dojde k velkému pohybu. Proto implementace OpenCV metody Lucas-Kanade přijímá pyramidy.

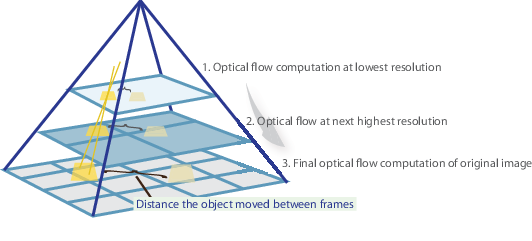
V high-level pohled, malé pohyby jsou zanedbané, jak jsme jít do pyramidy a velké pohyby jsou omezeny na malé pohyby – budeme počítat optický tok spolu s měřítkem. Komplexní matematické vysvětlení implementace OpenCV lze nalézt v bouguetových poznámkách a dokumentaci implementace Lucas-Kanade metody OpenCV pomocí calcOpticalFlowPyrLK() naleznete zde.

vizualizace

a je to! Otevřete Terminál a spusťte

python sparse-starter.py

otestujte si své řídký optický tok provádění. 👏

V případě, že jste vynechal nějaký kód, celý kód lze nalézt v sparse-solution.py.

implementace hustého optického toku

dříve jsme vypočítali optický tok pro řídkou sadu funkcí Pixelů. Hustý optický tok se pokouší vypočítat vektor optického toku pro každý pixel každého snímku. I když takový výpočet může být pomalejší, dává přesnější výsledek a hustší výsledek vhodný pro aplikace, jako je struktura učení z pohybu a segmentace videa. Existují různé implementace hustého optického toku. Budeme používat metodu Farneback, jednu z nejpopulárnějších implementací, s použitím OpenCV, open source knihovny algoritmů počítačového vidění, pro implementaci.

Nastavení prostředí

Pokud jste tak již neučinili, prosím, postupujte podle Kroku 1 prováděcího řídký optický tok nastavit své prostředí.

Další, otevřeno dense-starter.py s textovým editorem. Budeme psát celý kód v tomto souboru Pythonu.

Konfigurace OpenCV číst video

Farneback Optický Tok

Gunnar Farneback navrhla efektivní technika pro odhad pohybu zajímavých funkcí porovnáním dvou po sobě jdoucích snímků v jeho knize Dva-Snímek Odhad Pohybu Založené na Polynomiální Expanze.

nejprve metoda aproximuje okna (viz Lucas Kanade část implementace řídkého optického toku pro více podrobností) obrazových rámců kvadratickými polynomy prostřednictvím polynomiální expanzní transformace. Za druhé, pozorováním toho, jak se polynom transformuje pod translací (pohybem), je definována metoda odhadu polí posunutí z koeficientů polynomiální expanze. Po sérii zdokonalení se vypočítá hustý optický tok. Farnebackův papír je poměrně stručný a přímočarý, takže vřele doporučuji projít papír, pokud byste chtěli lépe porozumět jeho matematickému odvození.

Pro OpenCV je provádění, vypočítá velikost a směr optického toku z 2-kanálový pole proudění vektory \((dx/dt, dy/dt)\), optický tok problém. To pak vizualizuje úhel (směr) toku podle odstínu a vzdálenost (velikost) toku podle hodnoty HSV barevné reprezentace. Síla HSV je vždy nastavena na maximum 255 pro optimální viditelnost. Dokumentaci implementace metody Farneback OpenCV pomocí calcOpticalFlowFarneback() naleznete zde.

vizualizace

a je to! Otevřete terminál a spusťte

python dense-starter.py

, abyste otestovali implementaci hustého optického toku. 👏

V případě, že jste vynechal jakékoliv kódu, kompletní kód lze nalézt v dense-solution.py.

Optického Toku pomocí Hluboké Učení

Zatímco problém optického toku je historicky optimalizační problém, posledních přístupů použitím hluboké učení ukázaly působivé výsledky. Obecně tyto přístupy berou dva video snímky jako vstup pro výstup optického toku (barevně kódovaný obraz), který může být vyjádřen jako:

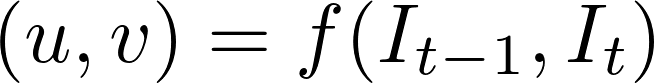
, kde \(u\) je pohyb v \(x\), \(v\) je pohyb v \(y\) směr, a \(f\) je neuronová síť, která má ve dvou po sobě jdoucích snímků, \(I_{t-1}\) (počet snímků v čase = \(t-1)\) a \(I_t\) (rám na čas = \(t)\) jako vstup.

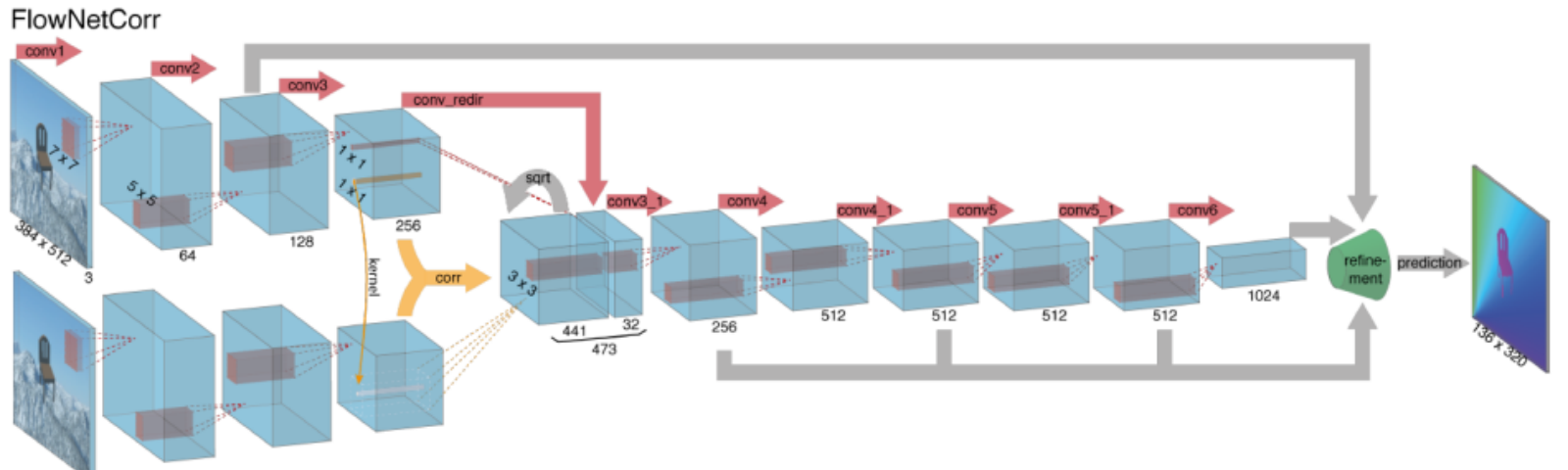
Výpočetní techniky optického toku s hluboké neuronové sítě vyžaduje velké množství trénovacích dat, které je obzvláště těžké získat. Je to proto, že označování videozáznamů pro optický tok vyžaduje přesné zjištění přesného pohybu každého bodu obrazu k přesnosti subpixelů. K řešení problému označování tréninkových dat vědci použili počítačovou grafiku k simulaci masivních realistických světů. Vzhledem k tomu, že světy jsou generovány instrukcí, je znám pohyb každého bodu obrazu ve video sekvenci. Některé příklady těchto zahrnují MPI-Sintel, open-source CGI film s optický tok označování vykreslen pro různé sekvence, a Létající Židle, dataset mnoho židlí létání přes náhodné pozadí také s optický tok značení.

Řešení optické problémy toku s hluboké učení je velmi horké téma v současné době, s variant FlowNet, SPyNet, PWC-Net, a více každý překonal jeden druhého na různých kritérií.

aplikace optického toku: sémantická segmentace

pole optického toku je obrovský důl informací pro pozorovanou scénu. Jak se techniky přesného určování optického toku zlepšují, je zajímavé vidět aplikace optického toku ve spojení s několika dalšími základními úkoly počítačových vizí. Například úkolem sémantické segmentace je rozdělit obraz do série regiony odpovídající unikátní objekt třídy ještě úzce umístěny objekty s identickými textury jsou často obtížné pro jeden snímek segmentace techniky. Pokud jsou objekty umístěny odděleně, nicméně, odlišné pohyby objektů mohou být velmi užitečné, pokud diskontinuita v hustém poli optického toku odpovídá hranicím mezi objekty.

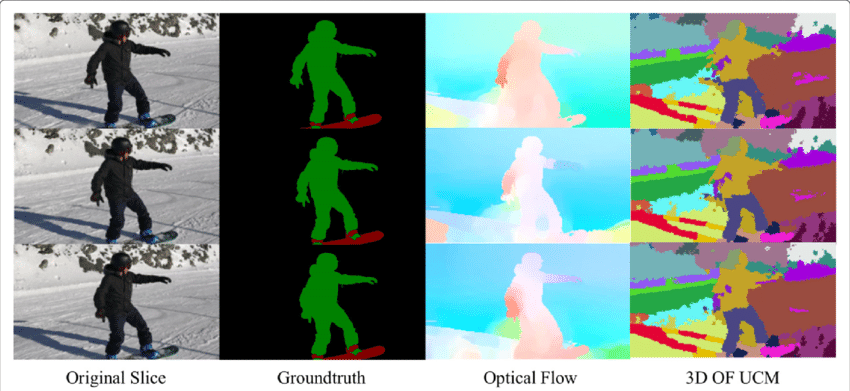
Optický Tok aplikace: Detekce Objektů & Sledování

Další slibné aplikace optického toku může být s objektem zjišťování a sledování, nebo, v high-úrovni formou, k budování real-time sledování vozidel a analýza provozu systémů. Od řídký optický tok od sledování bodů zájmu, jako je real-time systémů může být provedena pomocí funkce založené na optické techniky toku z buď ze stacionární kamery nebo kamery připevněné na vozidla.

Závěr

v Podstatě, optický tok vektorů funkce jako vstup do nesčetné množství vyšší-úrovni úkoly, které vyžadují scéna porozumění video sekvence, zatímco tyto úkoly mohou dále sloužit jako stavební bloky k ještě složitější systémy, jako jsou výraz obličeje analýzu, autonomní navigaci vozidel, a mnohem více. Nové aplikace pro optický tok, které ještě nebyly objeveny, jsou omezeny pouze vynalézavostí jeho návrhářů.

líný kód, nechcete utrácet na GPU? Vydejte se na Nanonety a vytvořte modely počítačového vidění zdarma!