Franck-Condon Princip popisuje intenzity vibronic přechody, nebo absorpcí nebo emisí fotonu. Uvádí, že když molekula prochází elektronickým přechodem, jako je ionizace, jaderná konfigurace molekuly nezaznamená žádnou významnou změnu. To je způsobeno tím, že jádra jsou mnohem masivnější než elektrony a elektronický přechod probíhá rychleji, než jádra mohou reagovat. Když se jádro přizpůsobí nové elektronické konfiguraci, teorie uvádí, že musí podstoupit vibraci.
Pokud jsme obrázek vertikální přechod ze země do excitovaného elektronického stavu, jako vyskytující se od vibrační vlnová funkce, která dává pravděpodobnost nalezení jader v dané oblasti prostoru můžeme určit pravděpodobnost, že dané vibrační úrovni, od přesahu integrál \(S_{v,v}\), která dává přesah vibrační vlnovou funkci v zemi a excitovaného stavu. Kvantová čísla \(v’\) odkazují na základní stav a kvantová čísla \(v\) odkazují na excitovaný stav. Pravděpodobnost přechodu může být rozdělena na elektronické a jaderné části pomocí Condonovy aproximace.
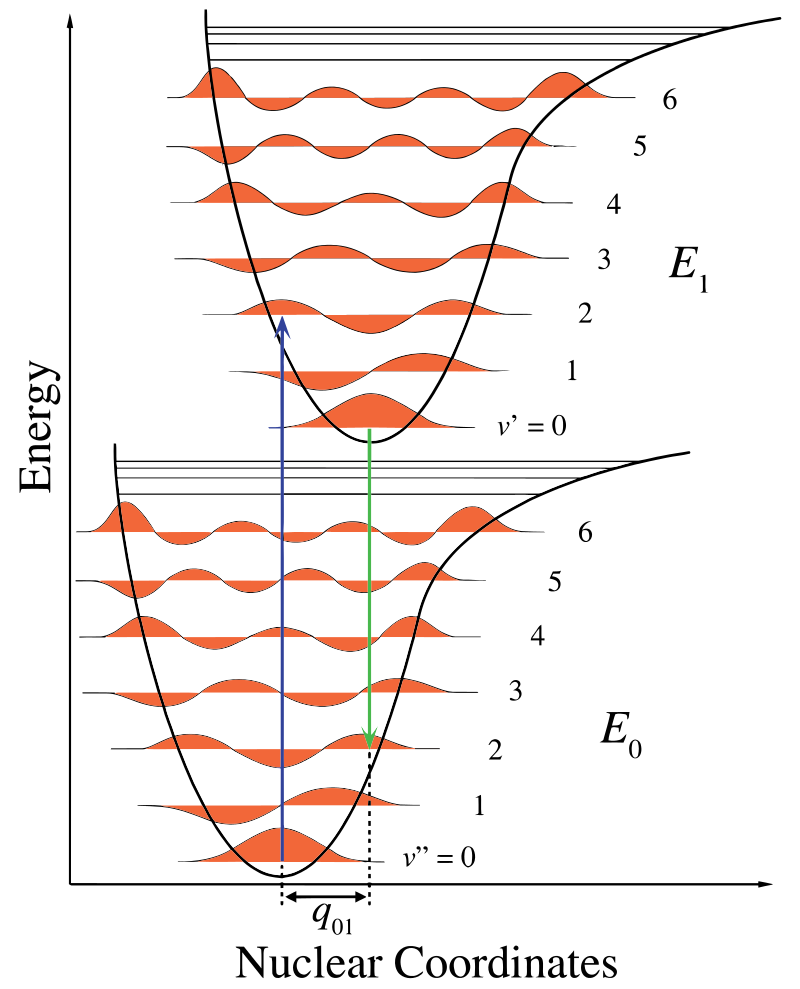
Na Obrázku \(\PageIndex{1}\), jaderné osa ukazuje důsledek internuclear oddělení a vibronic přechod je indikován pomocí modré a zelené svislé šipky. Toto číslo ukazuje tři věci:
- absorpce vede k vyšší energetický stav,
- fluorescenční vede k nižší energetický stav,
- posun v jaderných souřadnic mezi zemí a excitovaného stavu je orientační nové rovnovážné polohy pro jaderné interakce potenciál. Skutečnost, že fluorescenční šipka je kratší než absorpce, naznačuje, že má méně energie nebo že její vlnová délka je delší.
Klasické Condon sbližování
Condon aproximací je předpoklad, že elektronické přechodu dochází na časové měřítko krátké ve srovnání s jadernou pohybu tak, že přechodové pravděpodobnosti lze vypočítat na pevnou jaderné pozici.
tato změna vibrací je zachována během stavu nazývaného rychlé elektronické buzení. Výsledné Coulombické síly vytvářejí rovnováhu, jak je znázorněno na obrázku pro jádra nazývaná bod obratu. Bod obratu lze mapovat nakreslením svislé čáry od minima dolní křivky k průsečíku vyššího elektronického stavu. Tento postup se nazývá vertikální přechod a byl diskutován dříve v kontextu fotoelektronové spektroskopie (další elektronická spektroskopie)..
Franck-Condon Princip vysvětluje relativní intenzity vibronic přechody tím, o probablity of vibrační přechod k překrývání vibrační vlnové funkce. Uvádí se, že pravděpodobnost, že vibrační přechod vyskytující se vážený Franck-Condon překrývají integrálu:
\
v Rámci Franck-Condon sbližování, jádra jsou považována za „pevnou“ během elektronické přechody. Elektronické přechody lze tedy považovat za vertikální přechody na elektronických křivkách potenciální energie (vierické přechody na obrázku \(\PageIndex{1}\)).
kvantový Franck-Condonův princip
Franck-Condonův princip má klasickou i kvantovou aplikaci. Klasicky je Franck-Condonův princip aproximací, že elektronický přechod s největší pravděpodobností nastane bez změn pozic jader v molekulární entitě a jejím prostředí. Výsledný stav se nazývá Franck-Condonův stav a přechod, vertikální přechod. Kvantové mechanické formulaci této zásady je, že intenzita vibronic přechodu je úměrná čtverci překrývají nedílnou mezi vibrační wavefunctions dvou států, které jsou zapojeny v přechodu.
Franck-Condon princip je založen na Born-Oppenheimerově aproximaci, která umožňuje oddělení elektronických \(q\) a jaderné \(Q\) vlnové funkce vzhledem k celkové wavefunction.
\
Od přechodu operátor \(\hat{\mu}(q)\), je závislá pouze na elektronické komponenty, jaderné komponenty mohou být odděleny od přechodu okamžik integrální, které určuje pravděpodobnost přechodu vyskytující:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{jaderné překrývání}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
v Případě jaderné překrývání integrál je nulový na tento přechod, a pak ten přechod nebude dodržena, bez ohledu na velikost elektronického faktor.
\(S_{00}\) Přechod Hodnoceny v rámci Harmonický Oscilátor Model
jaderné překrývání pro nula-nula přechod \(S_{00}\) lze vypočítat poměrně jednoduše pomocí definice Gaussova podobě harmonického oscilátoru wavefunctions.
nulového bodu wavefunction v zemi elektronických stavu je,
\
nulového bodu wavefunction v excitovaného elektronického stavu je,
\
, kde
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(R_e\) je rovnovážná délka pouto v zemi elektronických státu
- \(Q_e\) je rovnovážná délka pouto v excitovaného elektronického stavu
jaderné překrývání integrál je
\
exponent v Rovnici \(\ref{FC1}\) může být rozšířena jako
\
a můžeme použít
\
a
\
nahradit a dokončit čtverec uvnitř integrálu. Můžeme vyjádřit
\.\]
integrál v rovnici \(\ref{FC2}\) je tedy
\
integrál je gaussovský integrál. Můžete ukázat, že dáme-li \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\), pak \(dz = \sqrt{\alpha} dR\) a integrál se stává
\
tento integrál byl řešen již z tabulky integrálů, Rovnice \(\ref{FC3}\) stává
\
Budeme následovat stejný postup pro výpočet, které se překrývají na nultou úroveň vibrací v zemi na první nadšený vibrační hladiny excitovaného stavu: \(S_{01}\).
\(S_{01}\) Přechod Hodnoceny v rámci Harmonický Oscilátor Model
Pro výpočet překrytí nultý zemi státní úrovni (\(v=0\)) s prvním vzrušený státní úrovni (\(v’=1\)), používáme Hermitova polynomu \(H_1(x) =2x\) pro popis excitovaného stavu wavefunction (viz zde recenzi na harmonický oscilátor wavefunctions). Zde \(x = \ sqrt {\alpha} (R – Q_e)\).
\
s nulovým bodem wavefunction v zemi elektronických stavu je,
\
první nadšený-státní wavefunction v excitovaného elektronického stavu je,
\
Překrytí nultý zemi státní úrovni prvního excitovaného stavu úrovně (Rovnice \(\ref{FC01}\)) je pak
\
a
\
stejné substituce může být provedena jako výše tak, že integrál lze napsat jako (není zobrazeno, a musí být prokázána v domácí cvičení) a konečný výsledek je
\
mohli Bychom pokračovat a vypočítat, které se překrývají na nultou úroveň v základním stavu s vyšší světlo vibrační úrovně: \(S_{02}\), \(S_{03}\), atd. Každý termín odpovídá přechodu s jinou energií, protože vibrační úrovně mají různé energie. Absorpční pásmo pak má vzhled progrese (Franck-Condonova progrese) přechodů mezi různými úrovněmi, z nichž každá má svou vlastní pravděpodobnost.
Franck-Condon Průběhy
pochopit význam výše uvedeného vzorce pro FC faktorem, podívejme se na zem a excitovaného stavu potenciální energie povrchu v \(T = 0\) Kelvin. Níže jsou uvedeny dva stavy oddělené energií 8 000 cm-1. Jedná se o oddělení energie mezi dnem jejich potenciálních jamek, ale také mezi příslušnými úrovněmi energie s nulovým bodem. Předpokládejme, že vlnočet z vibrační režim je 1000 cm-1 a že pouto, délka je zvýšena vzhledem k tomu, že elektron je odstraněn z lepení orbitální a umístěny v anti-lepení orbital na elektronické excitace.
Podle výše uvedeného modelu pro Franck-Condon faktor bychom generovat „držet“ spektra (Obrázek \(\PageIndex{3}\)), kde každý vibrační přechod je nekonečně úzký a přechod může nastat pouze tehdy, když \(E = h\nu\) přesně. Například potenciální energie povrchy byly uvedeny pro S = 1 a přechodové pravděpodobnosti na každé úrovni je dána hole (černá) na obrázku níže.
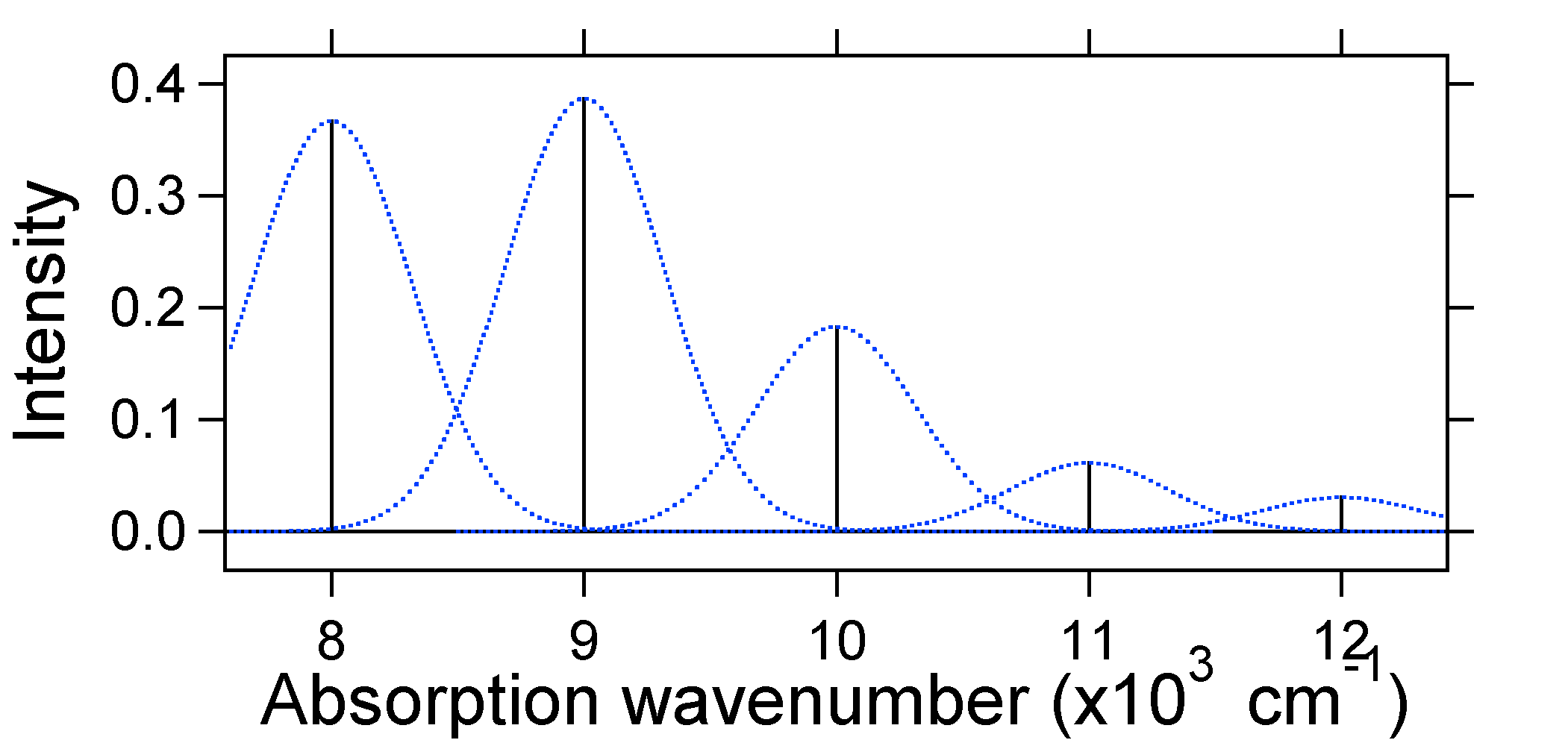
tečkovaných Gaussians, které obklopují každý držet poskytují realističtější obrázek o tom, co absorpční spektra by měla vypadat. Na tomto prvním místě bude každá energetická úroveň (hůl) dána určitou šířkou tím, že stát má konečnou životnost. Takové rozšíření se nazývá homogenní rozšíření, protože ovlivňuje všechny molekuly v souboru podobným způsobem. Existuje také rozšíření kvůli malým rozdílům v prostředí každé molekuly. Tento typ rozšíření se nazývá nehomogenní rozšíření. Bez ohledu na původ výše uvedený model byl vytvořen pomocí Gaussova rozšíření
jaderné posunutí mezi zemí a excitovaného stavu určuje tvar absorpční spektrum. Podívejme se jak na menší, tak na velké posunutí stavu. Pokud \(S = ½\) a potenciální energie povrchy, v tomto případě jsou:
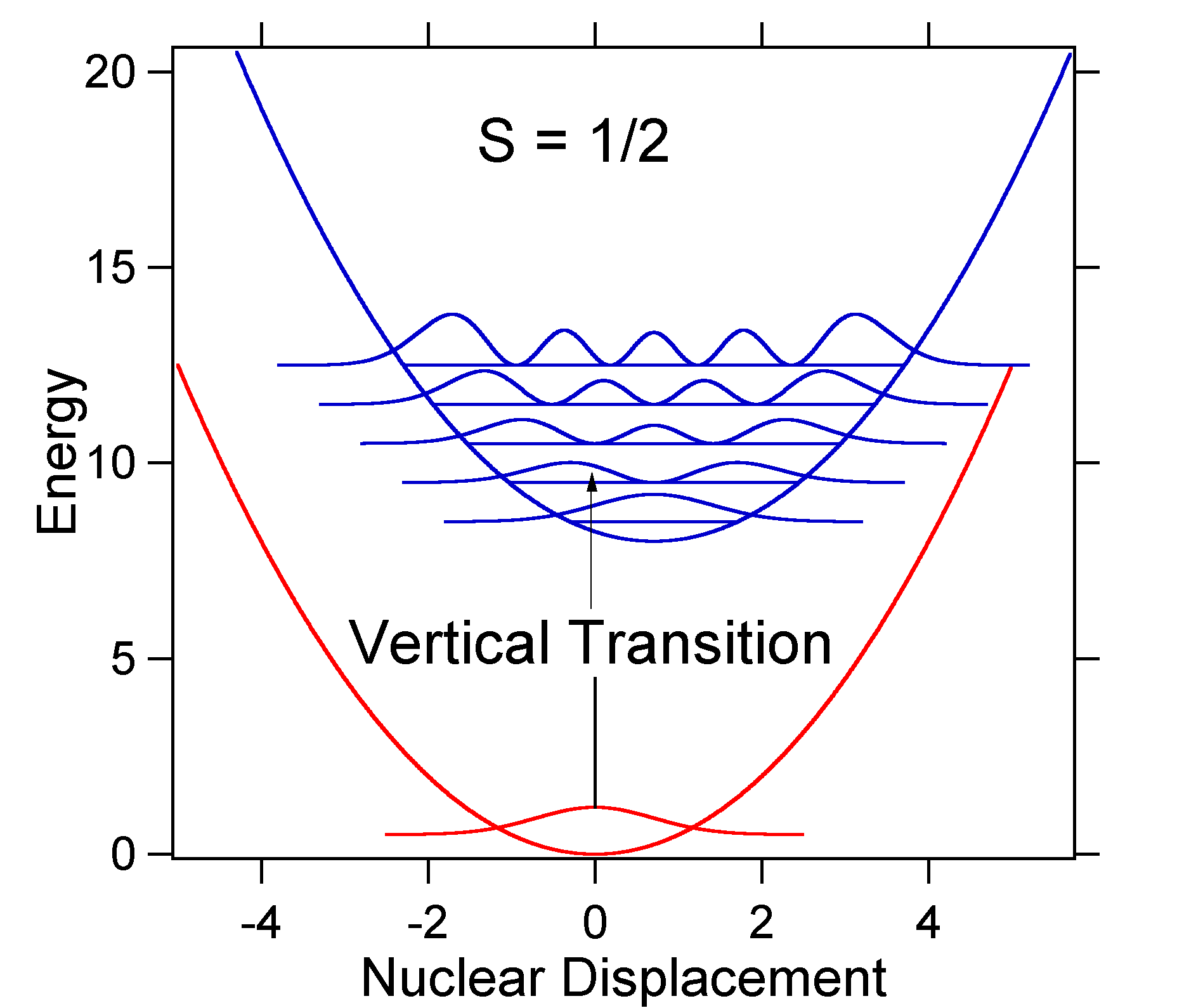
For this case the „stick“ spectrum has the appearance in Figure \(\PageIndex{5}\)
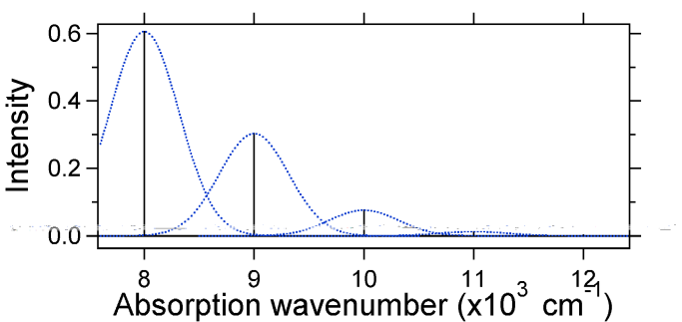
Všimněte si, že nula-nula nebo \(S_{0,0}\) vibrační přechod je moc velké v případě, že výtlak je malý.
obecně platí, že konstanta \(s\) udává poměr intenzity přechodu \(v = 2\) k přechodu \(v = 1\). V tomto případě, protože \(S = 0.5\), \(v=2\) přechod je 0.5 intenzita \(v=1\) přechod.
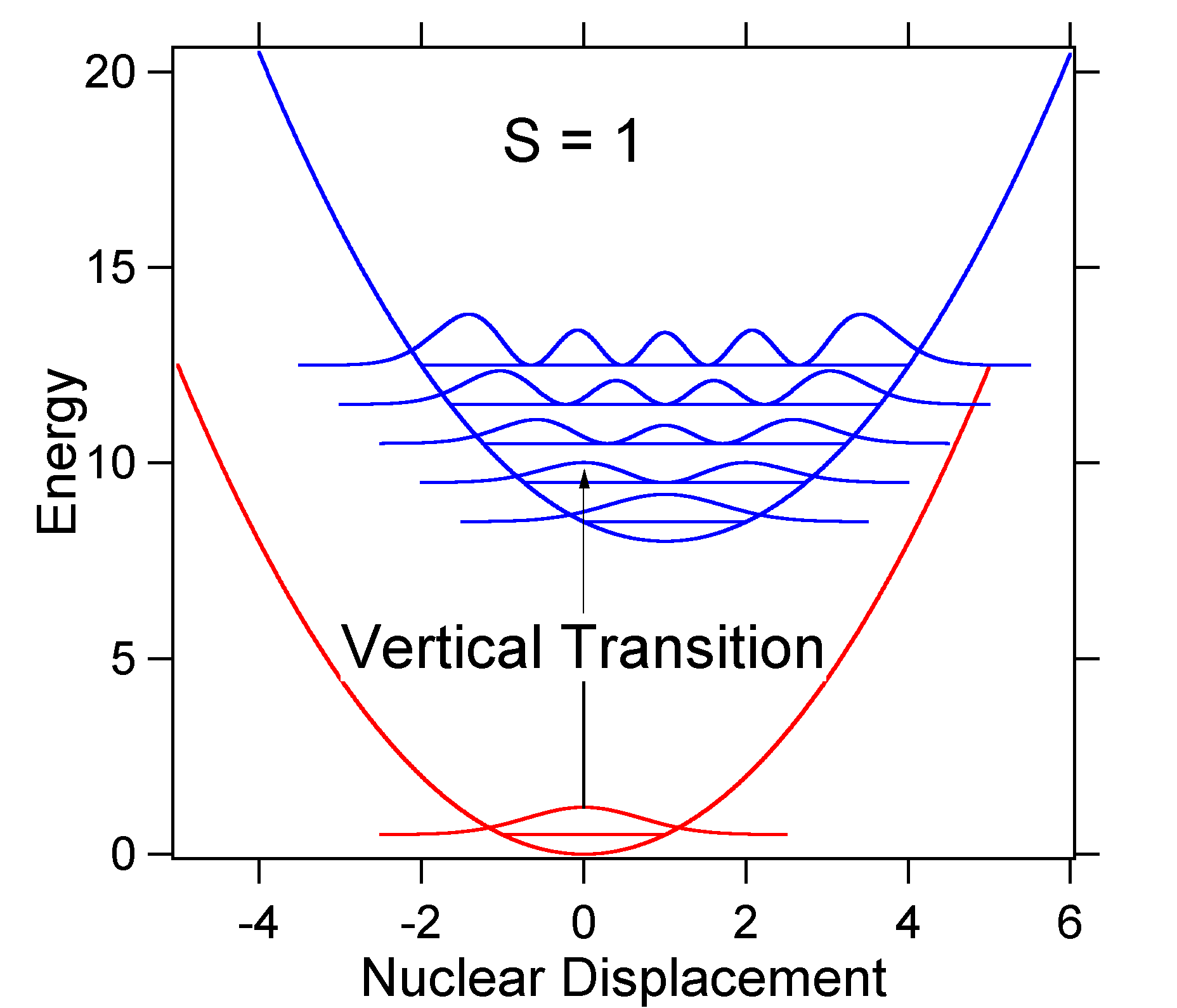
jako příklad většího posunu je dispozice potenciálních energetických ploch pro S = 2 uvedena níže.
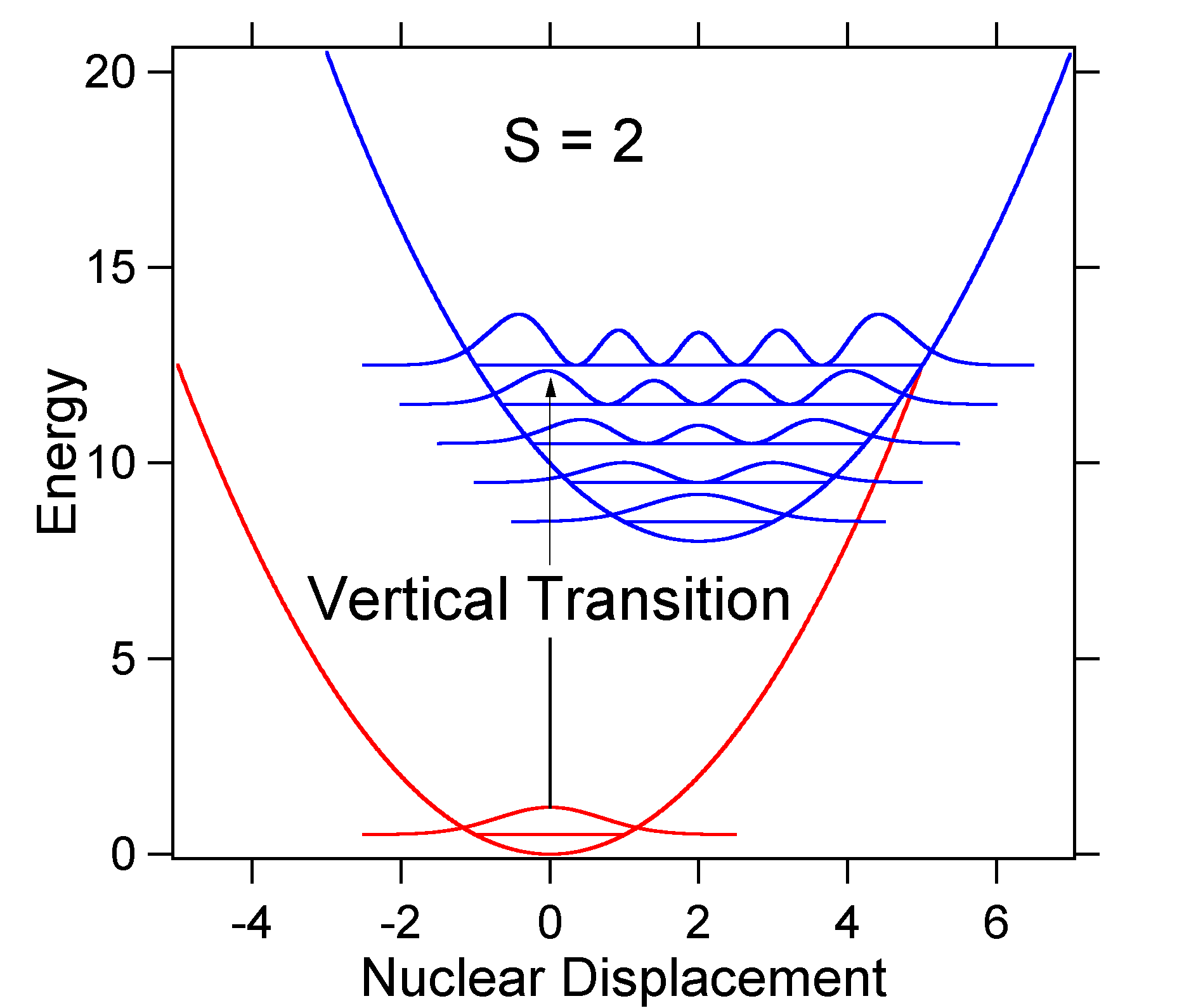
větší posun má za následek snížení překrývání zemi státní úrovni s v = 0 hladinu excitovaného stavu. Maximální intenzita bude dosažena ve vyšších vibračních úrovních, jak je znázorněno ve spektru tyčinek.
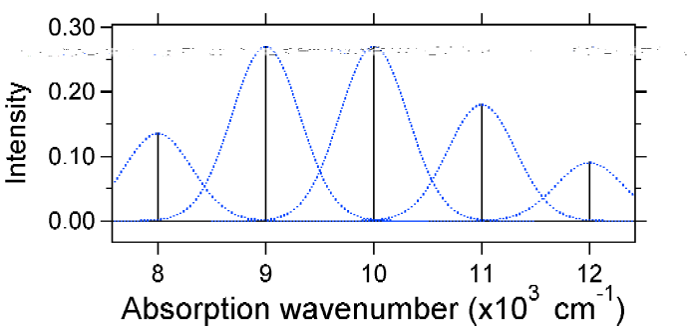
absorpční spektra vyneseny níže všechny mají stejný integrované intenzitu, nicméně jejich tvary jsou odlišné, protože se liší rozsah posunutí excitovaného stavu potenciální energie povrchu.
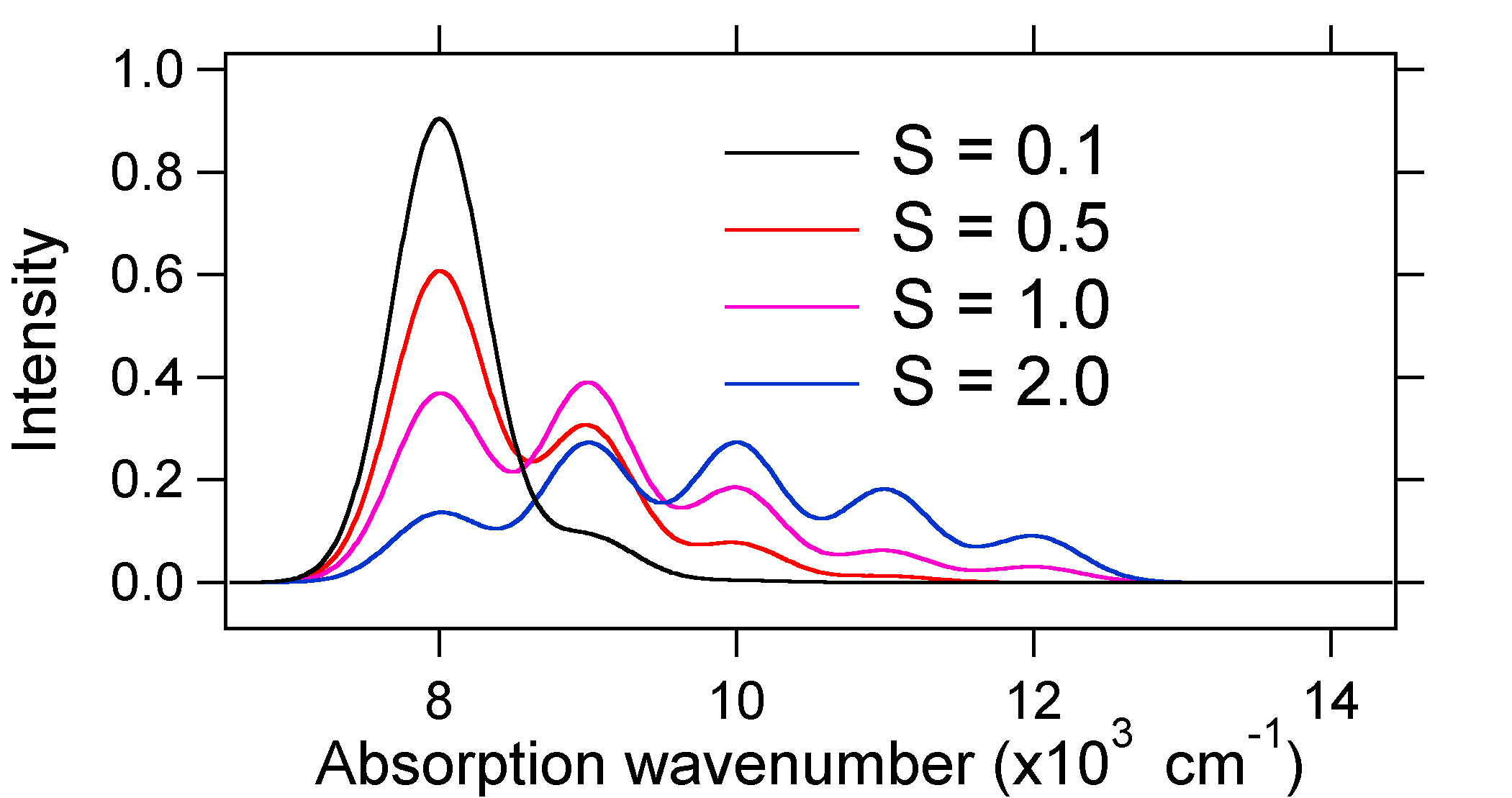
povaha relativní vibronic kapely míry nám může říct, zda je posunutí rovnováhy jaderných souřadnic, které doprovázely přechod. Kdy bude zvýšení bond length (tj. \(Q_e > R_e\))? K tomu dochází, když je elektron povýšen z vazebného molekulárního orbitalu na nevázané nebo anti-vazebné molekulární orbitaly(tj.
- Non-lepení molekulární orbital \(\rightarrow\) lepení molekulový orbital.
- Anti-lepení molekulární orbital \(\rightarrow\) lepení molekulový orbital.
- Anti-lepení molekulární orbital \(\rightarrow\) non-lepení molekulový orbital.
stručně řečeno, když bond, aby je nižší v excitovaném stavu než v základním stavu, pak \(Q_e > R_e\); zvýšení bondlength dojde, když se to stane.
- J. M. Luis, D. M. Bishop, B. Kirtman. Jiný přístup pro výpočet faktorů Franck-Condon včetně anharmonicity. J. Chem. Phys., 120 (2004), s. 813-822.
- Atkins, Peter a Julio de Paula. Fyzikální chemie pro vědy o živé přírodě. 2006. New York, NY: W. H. Freeman a společnost. s. 563-564
- Franck-Condonův princip. 1996, 68, 2243. IUPAC Kompendium chemické terminologie 2. vydání (1997). www.iupac.org/goldbook/F02510.pdf
- e. Rabinowitch a Govindjee. Absorpce světla a osud excitace energie. 1969. Franck-Condonův Princip. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Přispěvatelé
- Matthe Zi Ziering
-
Stefan Franzen (North Carolina State University)