Bez dozoru, Funkce Učení a Hluboké Učení Tutorial

Úvod

Analýzy Hlavních Komponent (PCA) je redukce dimenzionality algoritmus, který může být použit k výrazně zrychlit váš bez dozoru, funkce učení algoritmus. Ještě důležitější je, že porozumění PCA nám umožní později implementovat bělení, což je důležitý krok před zpracováním pro mnoho algoritmů.

Předpokládejme, že trénujete svůj algoritmus na obrázcích. Pak bude vstup poněkud nadbytečný, protože hodnoty sousedních pixelů v obraze jsou vysoce korelovány. Konkrétně předpokládejme, že trénujeme na obrázcích ve stupních šedi 16×16. Pak \textstyle x \ in \ Re^{256} jsou 256 rozměrových vektorů, přičemž jedna funkce \textstyle x_j odpovídá intenzitě každého pixelu. Vzhledem k korelaci mezi sousedními pixely nám PCA umožní přiblížit vstup s mnohem nižším rozměrem, zatímco vznikne velmi malá chyba.

Příklad a Matematické Pozadí

Pro náš příklad, budeme používat dataset, \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} \textstyle n=2 rozměrné vstupy, tak, že \textstyle x^{(i)} \in \Re^2. Předpokládejme, že chceme snížit data ze 2 rozměrů na 1. (V praxi bychom mohli chtít snížit data z 256 na 50 dimenzí, řekněme; ale použití nižších rozměrových dat v našem příkladu nám umožňuje lépe vizualizovat algoritmy.) Tady je náš datový soubor:

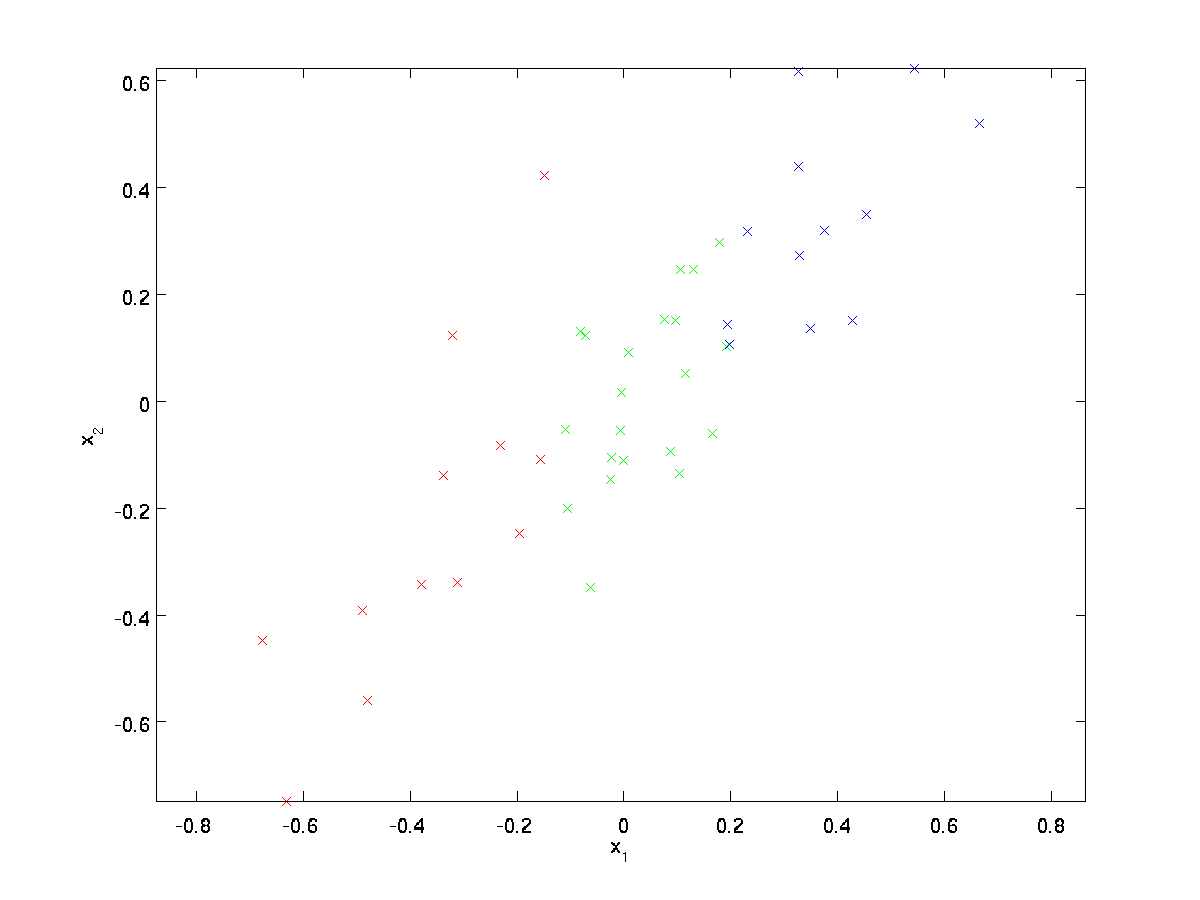
Tato data byla již předem zpracovány tak, aby každá funkce, \textstyle x_1, \textstyle x_2 mít zhruba stejný průměr (nula) a rozptyl.

pro ilustraci jsme také obarvili každý z bodů jednou ze tří barev, v závislosti na jejich \textstyle x_1 hodnota; tyto barvy nejsou používány algoritmem, a jsou pouze pro ilustraci.

PCA najde nižší dimenzionální podprostor, do kterého promítne naše data.
Z vizuálně zkoumá data, zdá se, že \textstyle u_1 je hlavní směr variability dat, a \textstyle u_2 sekundární směr odchylky:

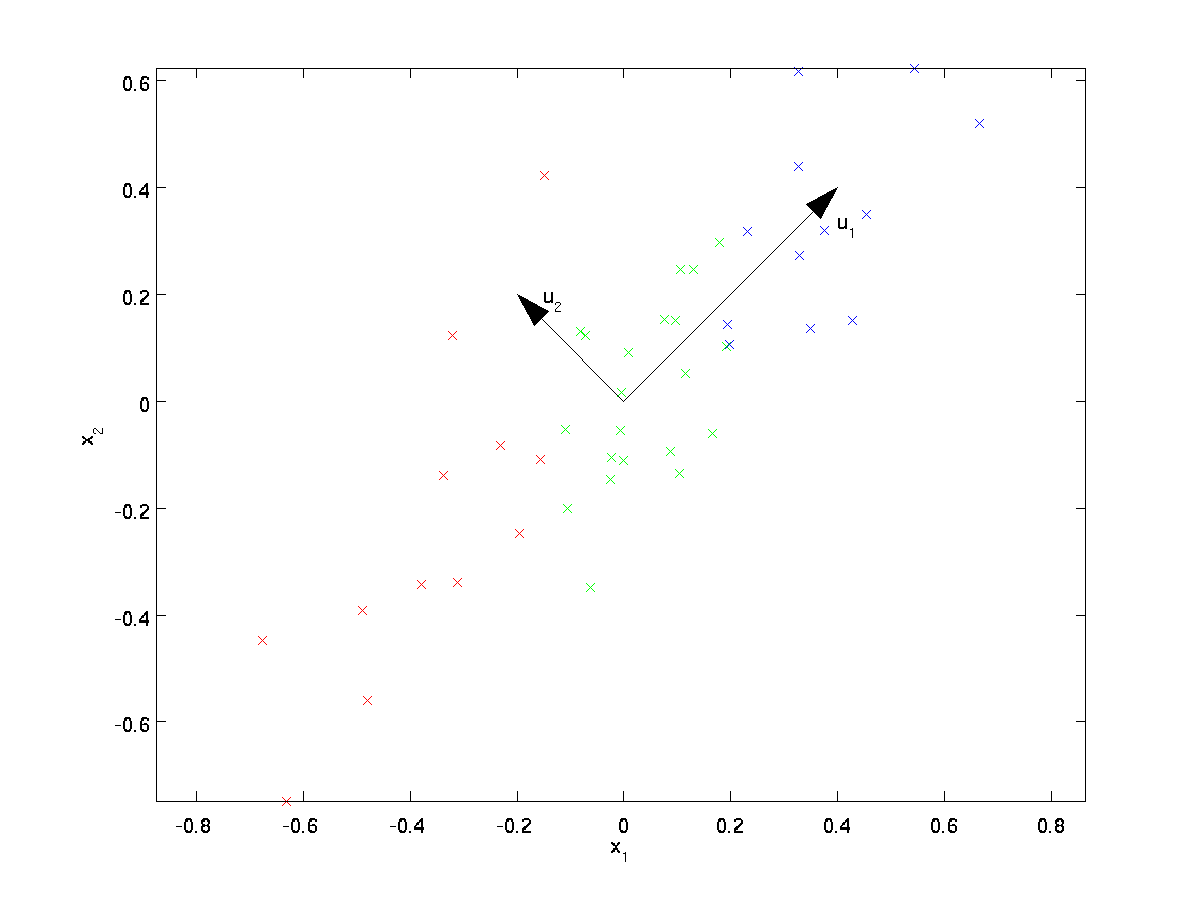
I. e., údaje se liší mnohem více ve směru \textstyle u_1, než \textstyle u_2. Abychom formálněji našli směry \textstyle u_1 a \textstyle u_2, nejprve vypočítáme matici \textstyle \Sigma následovně:

\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T \end{align}

Pokud \textstyle x má nulovou střední, pak \textstyle \Sigma je přesně to, kovarianční matice \textstyle x. (Symbol „\textstyle \Sigma“, vyslovuje se „Sigma“, je standardní notaci pro označení kovarianční matice. Bohužel to vypadá stejně jako symbol součtu, jako v \sum_{i=1}^n i; ale to jsou dvě různé věci.)

To pak může být prokázáno, že \textstyle u_1—hlavní směr variability dat—je horní (hlavní) vlastní vektor \textstyle \Sigma, \textstyle u_2 je druhý vlastní vektor.

Poznámka: Pokud máte zájem vidět více formální matematické odvození/odůvodnění tohoto výsledku, viz CS229 (Strojové Učení) skripta na PCA (odkaz v dolní části této stránky). Nebudete muset dělat tak, aby sledovat podél tohoto kurzu, nicméně.

k nalezení těchto vlastních vektorů můžete použít standardní numerický lineární algebraický software (viz Poznámky k implementaci). Konkrétně, dejte nám vypočítat vlastní vektory \textstyle \Sigma, a skládat vlastní vektory ve sloupcích tvoří matice \textstyle U:

\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}

Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.

vektory \textstyle u_1, \textstyle u_2 v našem příkladu tvoří nový základ, ve kterém můžeme reprezentovat data. Konkrétně nechť \textstyle x \ in \ Re^2 je nějaký tréninkový příklad. Pak \textstyle u_1^Tx je délka (velikost) projekce \textstyle x na vektor \textstyle u_1.

Podobně, \textstyle u_2^Tx je velikost \textstyle x promítá na vektor \textstyle u_2.

Rotující Údaje

můžeme Tedy reprezentovat \textstyle x v \textstyle (u_1, u_2)-základ o počítání,

\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}

(dolní index „rot“ pochází z pozorování, že to odpovídá rotaci (a možná i zamyšlení) původní data.) Umožňuje vzít celou sadu školení, a vypočítat \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} pro každé \textstyle jsem. Vykreslování tato transformovaná data \textstyle x_{\rm rot}, dostaneme:

Toto je trénink set otáčet do \textstyle u_1,\textstyle u_2 základě. V obecném případě, \textstyle U^Tx bude trénovací množina otáčet na základě \textstyle u_1,\textstyle u_2, …,\textstyle u_n.

Jednou z vlastností \textstyle U je, že se jedná o „ortogonální“ matrix, což znamená, že splňuje \textstyle U^TU = UU^T = I. Takže pokud jste někdy muset jít z otočené vektory \textstyle x_{\rm rot} zpět na původní data \textstyle x, můžete vypočítat,

\begin{align}x = U x_{\rm rot} ,\end{align}

protože \textstyle U x_{\rm rot} = UU^T x = x.

Snížení Dimension Data

vidíme, že hlavní směr variability dat je první rozměr, \textstyle x_{\rm rot,1} z této otáčet údajů. Tedy, chceme-li snížit tato data na jeden rozměr, můžeme

\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}

Více obecně platí, že pokud \textstyle x \in \Re^n a chceme snížit na \textstyle k dimenzionální reprezentace \textstyle \tilde{x} \in \Re^k (kde k < n), budeme mít první \textstyle k složky \textstyle x_{\rm rot}, které odpovídají horní \textstyle k nasměrování variace.

dalším způsobem vysvětlení PCA je, že \textstyle x_{\RM rot} je \ textstyle n dimenzionální vektor, kde prvních několik komponent bude pravděpodobně velkých (např. v našem příkladu jsme viděli, že \textstyle x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} trvá přiměřeně velké hodnoty pro většinu příklady \textstyle já), a později součástí jsou pravděpodobné, že bude malý (např. v našem příkladu, \textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)} více pravděpodobné, že bude malý). Co PCA dělá to to klesne na novější (menší) složky \textstyle x_{\rm rot}, a jen sbližuje je s 0. Konkrétně, naše definice \textstyle \tilde{x} může být také dorazili pomocí aproximace \textstyle x_{\rm rot}, kde jsou všechny ale první \textstyle k součásti jsou nuly. Jinými slovy, máme:

\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{align}

V našem příkladu, to nám dává následující děj \textstyle \tilde{x} (pomocí \textstyle n=2, k=1):

Nicméně, od poslední \textstyle n-k složek \textstyle \tilde{x}, jak je definován výše, by mělo být vždy nulová, není třeba, aby tyto kolem nuly, a tak jsme se definovat, \textstyle \tilde{x} jako \textstyle k-dimenzionální vektor s první \textstyle k (non-nula) komponenty.

To také vysvětluje, proč jsme chtěli vyjádřit naše data v \textstyle u_1, u_2, \ldots, u_n základ: Rozhodování o tom, které komponenty udržet se stává jen udržet top \textstyle k součásti. Když to uděláme, říkáme také ,že jsme “ zachování horní \textstyle k PCA (nebo hlavní) komponenty.“

Zotavuje Aproximace Dat

Nyní, \textstyle \tilde{x} \in \Re^k je nižší-dimenzionální, „stlačený“ reprezentace původního \textstyle x \in \Re^n. Vzhledem \textstyle \tilde{x}, jak můžeme obnovit aproximace \textstyle \hat{x} na původní hodnotu \textstyle x? Z dřívější části víme, že \textstyle x = u x_{\rm rot}. Dále můžeme myslet, \textstyle \tilde{x} jako aproximace \textstyle x_{\rm rot}, kde máme poslední \textstyle n-k komponent do nuly. Tak, vzhledem k tomu, \textstyle \tilde{x} \in \Re^k, můžeme pad s \textstyle n-k nul, aby se naše sbližování s \textstyle x_{\rm rot} \in \Re^n. Nakonec jsme pre-vynásobte \textstyle U, aby se naše sbližování s \textstyle x. Konkrétně, dostaneme

\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}já. \end{align}

konečná rovnost výše pochází z definice \textstyle U uvedené dříve. (V praktické implementaci, bychom neměli vlastně žádné pad \textstyle \tilde{x} a pak vynásobte \textstyle U, protože to by znamenalo, násobení spoustu věcí od nuly; místo toho, jen bychom násobit \textstyle \tilde{x} \in \Re^k s první \textstyle k sloupců \textstyle U jako v posledním výrazu výše.) Použitím tohoto na náš datový soubor získáme následující graf pro \textstyle \hat{x}:

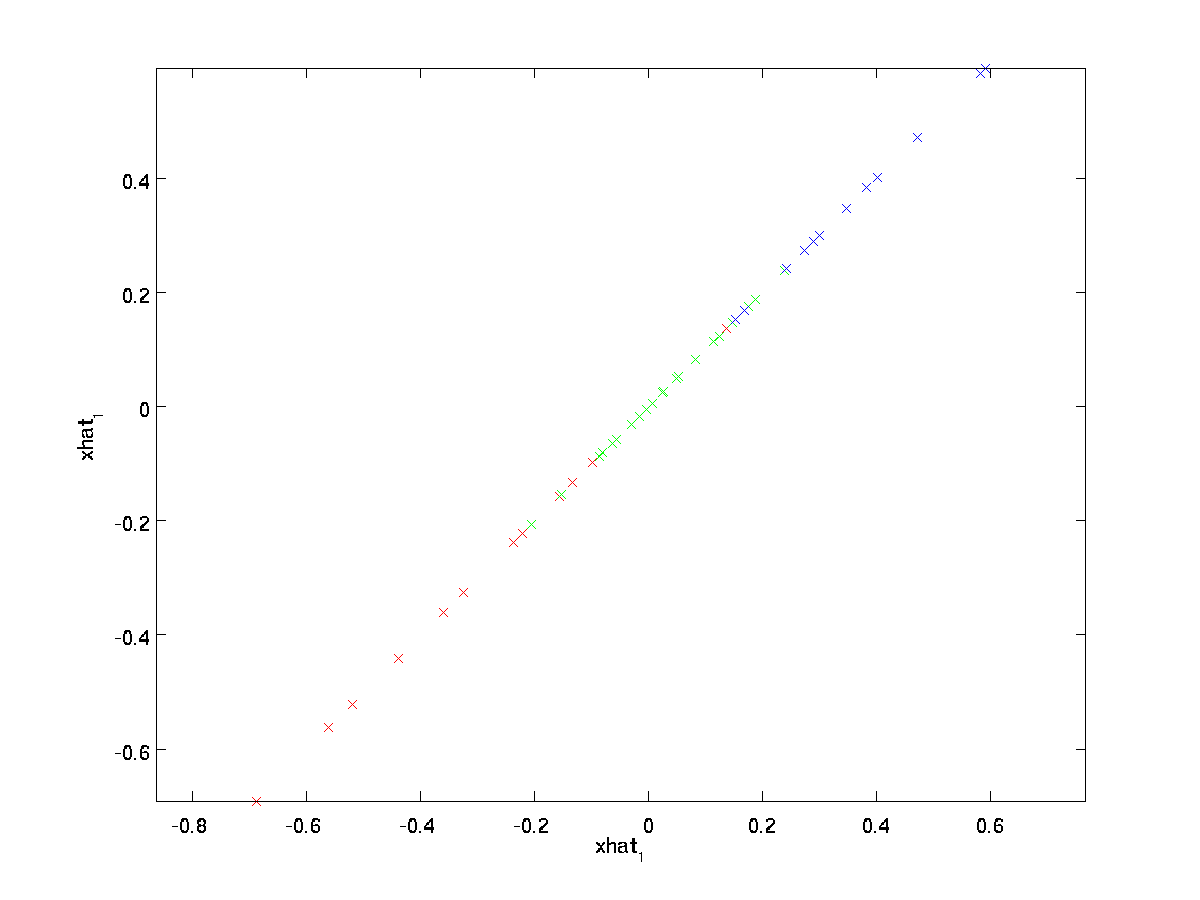
Jsme tedy pomocí 1 dimenzionální aproximace původní dataset.

pokud trénujete autoencoder nebo jiný algoritmus učení funkcí bez dozoru, bude doba běhu vašeho algoritmu záviset na rozměru vstupu. Pokud krmíte \textstyle \tilde{x} \in \Re^k do učení algoritmus místo \textstyle x, pak budete mít trénink na nižší-dimenzionální vstupní, a tak váš algoritmus může běžet výrazně rychleji. Pro mnoho datových souborů, nižší dimenzionální \textstyle \tilde{x} zastoupení může být velmi dobrou aproximací originálu, a pomocí PCA tímto způsobem můžete výrazně zrychlit váš algoritmus při zavádění velmi málo sbližování právních chyb.

Počet komponent udržet

Jak nastavit \textstyle k; tj., kolik PCA komponent bychom měli zachovat? V našem jednoduchém 2 dimenzionálním příkladu se zdálo přirozené zachovat 1 ze 2 složek, ale pro vyšší rozměrná data je toto rozhodnutí méně triviální. Pokud \textstyle k je příliš velký, pak nebudeme komprese dat; v limitu \textstyle k=n, pak jsme jen s použitím původní data (ale otáčet na jiném základě). Naopak, pokud \textstyle k je příliš malý, pak bychom mohli používat velmi špatnou aproximaci dat.

rozhodnout, jak nastavit \textstyle k, budeme obvykle podívejte se na „‚procento rozptylu udržel“‚ pro různé hodnoty \textstyle k. Konkrétně, pokud \textstyle k=n, pak máme přesné přiblížení na údaje, a můžeme říci, že 100% rozptyl je zachován. Tedy., všechny variace původních dat jsou zachovány. Naopak, pokud \textstyle k=0, pak aproximujeme všechna data nulovým vektorem, a tak zůstává zachováno 0% rozptylu.

Více obecně, ať \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n být vlastní čísla \textstyle \Sigma (řazeny v sestupném pořadí) tak, že \textstyle \lambda_j je vlastní číslo odpovídající vlastní vektor \textstyle u_j. Pak, když jsme se zachovat \textstyle k hlavních komponent, procento rozptylu zachován je dána:

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\end{align}

v našem jednoduchém 2D příkladu výše, \textstyle \ lambda_1 = 7.29 a \textstyle \lambda_2 = 0.69. Tak, tím, že drží pouze \textstyle k=1 hlavních komponent jsme zachován \textstyle 7.29/(7.29+0.69) = 0.913, nebo 91.3% rozptylu.

formálnější definice zachovaného procenta rozptylu je nad rámec těchto poznámek. Je však možné ukázat,že \textstyle \lambda_j =\sum_{i=1}^m x_{\rm rot, j}^2. Tedy, v případě, \textstyle \lambda_j \cca 0, který ukazuje, že \textstyle x_{\rm rot,j} je obvykle v blízkosti 0 stejně, a my se ztratit relativně málo sblížením s konstantní 0. To také vysvětluje, proč si ponecháváme horní hlavní komponenty (odpovídající větším hodnotám \textstyle \lambda_j) místo spodních. Horní hlavní složky \textstyle x_{\rm rot,j} jsou ty, které jsou více variabilní, a že se na větší hodnoty, a pro které bychom vynakládat větší sbližování chyba, pokud jsme je nastavit na nulu.

V případě obrázků, jeden společný heuristické, je vybrat \textstyle k tak, aby zachovat 99% rozptylu. Jinými slovy, vybereme nejmenší hodnotu \textstyle k, která splňuje

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}

V závislosti na aplikaci, pokud jste ochotni způsobit nějakou další chybu, někdy se také používají hodnoty v rozsahu 90-98%. Když jsi popsat ostatním, jak jste použili PCA, říká, že jste si vybrali \textstyle k udržet 95% rozptylu bude také mnohem snadněji interpretovatelný popis, než tím, že si udržel 120 (nebo jakékoli jiné číslo) komponenty.

PCA na Obrázky

Pro PCA do práce, obvykle chceme, aby každá funkce, \textstyle x_1, x_2, \ldots, x_n mají podobný rozsah hodnot pro ostatní (a mít na mysli blíží nule). Pokud jste použili PCA na jiné aplikace, než může mít proto zvlášť pre-zpracované jednotlivé funkce mají nulovou střední hodnotou a jednotkovým rozptylem, samostatně odhad střední hodnoty a rozptylu pro každou funkci \textstyle x_j. Nicméně, tohle není pre-zpracování, které budeme aplikovat na většinu typů obrázků. Konkrétně, že jsme školení, že náš algoritmus na „přírodní obrazy“, tak, že \textstyle x_j je hodnota pixelu \textstyle j. „Přírodní obrazy,“ bychom neformálně říct typu obrazu, které je typické zvíře nebo člověk může vidět po celou dobu jejich životnosti.

Poznámka: Obvykle používáme obrazy venkovních scén s trávou, stromy atd., a vystřihnout malé (řekněme 16×16) obraz záplaty náhodně z nich trénovat algoritmus. Ale v praxi nejvíce funkce učení algoritmy jsou velmi robustní, aby přesně typ snímku, který je vyškolen, takže většina snímků pořízených s normální kamerou, tak dlouho, dokud nejsou příliš rozmazané nebo mají podivné artefakty, měl by fungovat.

při tréninku na přirozené obrazy nemá smysl odhadnout samostatný průměr a rozptyl pro každý pixel, protože statistiky v jedné části obrazu by měly být (teoreticky) stejné jako všechny ostatní.
tato vlastnost obrazů se nazývá „‚ stacionarita.“‚

podrobně, aby PCA fungovala dobře, neformálně požadujeme, aby (i) vlastnosti měly přibližně nulový průměr a (ii) různé vlastnosti měly podobné odchylky. S přirozenými obrazy je (ii)již spokojen i bez normalizace rozptylu, a proto nebudeme provádět normalizaci rozptylu.
(Pokud jste školení na audio data—řekněme, na spektrogramy—nebo na textová data—řekněme, bag-of-slovo vektorů—budeme obvykle nelze provést rozptyl normalizace.)
ve skutečnosti je PCA invariantní vůči škálování dat a vrátí stejné vlastní vektory bez ohledu na měřítko vstupu. Formálněji, pokud vynásobíte každý prvek vector \ textstyle x nějakým kladným číslem (tedy škálování každé funkce v každém příkladu tréninku stejným číslem), výstupní vlastní vektory PCA se nezmění.

takže nebudeme používat normalizaci rozptylu. Jedinou normalizací, kterou musíme provést, je průměrná normalizace, abychom zajistili, že funkce budou mít průměr kolem nuly. V závislosti na aplikaci se velmi často nezajímáme o to, jak jasný je celkový vstupní obraz. Například v úlohách rozpoznávání objektů nemá celkový jas obrazu vliv na to, jaké objekty jsou v obraze. Formálně nás nezajímá střední hodnota intenzity obrazové záplaty; můžeme tedy tuto hodnotu odečíst jako formu střední normalizace.

Konkrétně, pokud \textstyle x^{(i)} \in \Re^{n} jsou (ve stupních šedi) intenzita hodnoty 16×16 obrazových patch (\textstyle n=256), můžeme normalizovat intenzitu každého obrázku \textstyle x^{(i)} takto:

\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n-x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}

pro všechny, \textstyle j

Všimněte si, že dva výše uvedené kroky se provádí odděleně pro každý obrázek \textstyle x^{(i)}, a \textstyle \mu^{(i)} tady je střední intenzita obrazu \textstyle x^{(i)}. Zejména to není totéž jako odhad střední hodnoty zvlášť pro každý pixel \ textstyle x_j .

Pokud jste školení vaše algoritmus na obrázky jiné než přírodní obrázky (např. obrázky, ručně psané znaky nebo obrázky z jediné izolované objekty na střed proti bílému pozadí), jiné typy normalizace může být stojí za zvážení, a nejlepší volbou může být aplikace závislá. Ale při výcviku na přirozených obrazech by použití metody průměrné normalizace na obrázek, jak je uvedeno ve výše uvedených rovnicích, bylo rozumným výchozím bodem.

bělení

použili jsme PCA ke zmenšení rozměru dat. Existuje úzce související předzpracovací krok zvaný bělení (nebo, v některých jiných literaturách, sférování), který je potřebný pro některé algoritmy. Pokud trénujeme obrázky, surový vstup je redundantní, protože sousední hodnoty pixelů jsou vysoce korelovány. Cílem bělení je, aby se vstupní méně redundantní; více formálně, náš desiderata jsou, že naše algoritmy učení vidí vstupní školení, kde (i) funkce, které jsou méně v korelaci s navzájem, a (ii) funkce, které všechny mají stejný rozptyl.

2D příklad

nejprve popíšeme bělení pomocí našeho předchozího 2D příkladu. Poté popíšeme, jak to lze kombinovat s vyhlazováním, a nakonec jak to kombinovat s PCA.

Jak můžeme učinit naše vstupní funkce navzájem nekorelovanými? Už jsme to udělali při výpočtu \textstyle x_{\rm rot}^{(i)} = u^Tx^{(i)}.
Opakovat náš předchozí obrázek, naše pozemek pro \textstyle x_{\rm rot} byla:

kovarianční matice tohoto údaje je dána tím, že:

\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\end{align}

(Poznámka: Technicky bude mnoho tvrzení v této části o“ kovarianci “ pravdivé, pouze pokud budou mít data nulový průměr. Ve zbytku této části budeme tento předpoklad považovat za implicitní v našich prohlášeních. Nicméně, i když průměr dat není přesně nulový, intuice, které zde prezentujeme, stále platí, a tak se toho nemusíte bát.)

není náhodou, že diagonální hodnoty jsou \textstyle \lambda_1 a \textstyle \lambda_2. Dále, položky mimo diagonální jsou nulové; tedy, \textstyle x_{\rm rot,1} a \textstyle x_{\rm rot,2} jsou nekorelované, uspokojení jednoho z našich desiderata pro bělený dat (funkce, být méně korelované).

, Aby se každý z našich vstupní funkce mají jednotky rozptylu, můžeme jednoduše škálovat každou funkci \textstyle x_{\rm rot,i} v \textstyle 1/\sqrt{\lambda_i}. Konkrétně, budeme definovat naše bělený data \textstyle x_{\rm PCAwhite} \in \Re^n takto:

\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}

Vykreslování \textstyle x_{\rm PCAwhite}, dostaneme:

Tato data nyní má kovariance rovna jednotkové matice \textstyle I. řekneme, že \textstyle x_{\rm PCAwhite} je naše PCA bělený verze dat: jednotlivé složky \textstyle x_{\rm PCAwhite} jsou nekorelované a mají jednotkovou varianci.

bělení v kombinaci s redukcí rozměru. Pokud chcete mít data, která je bělený a která je nižší dimenzionální než původní vstup, můžete také volitelně udržet pouze horní \textstyle k složky \textstyle x_{\rm PCAwhite}. Když zkombinujeme bělení PCA s regularizací (popsanou později), posledních několik komponent \textstyle x_{\rm PCAwhite} bude stejně téměř nulové, a tak může být bezpečně upuštěno.

ZCA Whitening

nakonec se ukázalo, že tento způsob, jak získat data, aby měla kovariance identity \textstyle I, není jedinečný. Konkrétně, pokud \textstyle R je libovolná ortogonální matice, tak že to splňuje \textstyle RR^T = R^TR = I (méně formálně, pokud \textstyle R je rotace/reflexe matice), pak \textstyle R \,x_{\rm PCAwhite} bude mít také identitu kovariance.

V ZCA zubů, zvolíme \textstyle R = U. Budeme definovat

\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}

Kreslení \textstyle x_{\rm ZCAwhite}, dostaneme:

To může být prokázáno, že ze všech možných voleb pro \textstyle R, tato volba rotace způsobuje, \textstyle x_{\rm ZCAwhite} být tak blízko, jak je to možné, aby původní vstupní data \textstyle x.

Při použití ZCA zubů (na rozdíl od PCA s bělení), obvykle máme všechny \textstyle n rozměry dat, a nesnažte se snížit jeho velikost.

Regularizaton

Při provádění PCA s bělení nebo ZCA bělení v praxi, někdy některé z vlastních čísel \textstyle \lambda_i bude číselně blízko k 0, a tedy škálování krok, kde můžeme rozdělit podle \sqrt{\lambda_i} by znamenalo dělení hodnoty blízké nule; to může způsobit, že data vyhodit do povětří (vzít na velké hodnoty), nebo jinak být numericky nestabilní. V praxi, jsme se proto realizovat tento škálování krok pomocí malého množství regularizace, a přidat malé konstantní \textstyle \epsilon na vlastní čísla, než začnete jejich odmocniny a převrácené:

\ begin{align}x_{\rm PCAwhite, i} = \ frac{x_{\RM rot, i} } {\sqrt {\lambda_i + \epsilon}}.\end{align}

když \textstyle x vezme hodnoty kolem \textstyle, může být typická hodnota \textstyle \epsilon \ cca 10^{-5}.

v případě obrázků má přidání \textstyle \epsilon také za následek mírné vyhlazení (nebo filtrování dolního průchodu) vstupního obrazu. To také má žádoucí účinek odstranění aliasing artefakty způsobené způsob pixelů jsou stanoveny v obrázku, a může zlepšit funkce dozvěděl (podrobnosti jsou nad rámec těchto poznámek).

ZCA whitening je forma předběžného zpracování dat, která je mapuje od \textstyle x do \textstyle x_{\rm zcawhite}. Ukazuje se, že je to také hrubý model toho, jak biologické oko (sítnice) zpracovává obrazy. Konkrétně, jak vaše oko vnímá obrázky, Většina sousedních „pixelů“ve vašem oku bude vnímat velmi podobné hodnoty, protože sousední části obrazu mají tendenci být intenzivně korelovány. Je tedy zbytečné, aby vaše oko muselo přenášet každý pixel samostatně (prostřednictvím zrakového nervu) do mozku. Místo toho, vaše sítnice provádí decorrelation provoz (to se provádí pomocí retinálních neuronů, které počítají funkce tzv. „na střed, off surround/vypnuto center, surround“), který je podobný tomu, který provádí ZCA. To má za následek méně redundantní reprezentaci vstupního obrazu, který je pak přenášen do vašeho mozku.

Provedení PCA Zubů

V této části jsme shrnuli PCA, PCA s bělení a ZCA bělení algoritmy, a také popsat, jak se můžete realizovat pomocí efektivní lineární algebry knihoven.

nejprve musíme zajistit, aby data měla (přibližně) nulový průměr. U přirozených obrázků toho dosáhneme (přibližně) odečtením střední hodnoty každé obrazové záplaty.

toho dosáhneme výpočtem průměru pro každou opravu a odečtením pro každou opravu. V prostředí Matlab, můžeme to udělat pomocí

 avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);

Next, musíme vypočítat \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Pokud jste provádění tohoto v Matlabu (nebo i když jste se provádí v C++, Java, atd., ale mít přístup k efektivní knihovně lineární algebry), dělat to jako explicitní součet je neefektivní. Místo toho to můžeme vypočítat jedním pádem jako

 sigma = x * x' / size(x, 2);

(Zkontrolujte správnost matematiky sami.) Zde předpokládáme, že x je datová struktura, která obsahuje jeden tréninkový příklad na sloupec (takže x je matice \textstyle n-by-\textstyle m).

dále PCA vypočítá vlastní vektory \Sigma. Dalo by se to provést pomocí funkce Matlab eig. Nicméně, protože \Sigma je symetrická kladná semi-definitivní matice, je číselně spolehlivější to udělat pomocí funkce svd. Konkrétně, pokud budete implementovat,

 = svd(sigma);

pak matice U bude obsahovat vlastní vektory \Sigma (jeden vlastní vektor za sloupce seřazeny v pořadí od shora dolů eigenvector), a diagonální položky matice Y bude obsahovat odpovídající vlastní čísla (také řazeny v sestupném pořadí). Matice V se bude rovnat U a může být bezpečně ignorována.

(Poznámka: Svd funkce vlastně počítá singulární vektory a singulární hodnoty matice, která je pro speciální případ symetrické pozitivně semi-definitní matice—což je vše, co jsme se tady—se rovná jeho vlastní vektory a vlastní čísla. Úplná diskuse o singulárních vektorech vs. vlastní vektory je nad rámec těchto poznámek.)

a Konečně, můžete vypočítat \textstyle x_{\rm rot} a \textstyle \tilde{x} takto:

 xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keep

To dává PCA reprezentace dat, pokud jde o \textstyle \tilde{x} \in \Re^k. Mimochodem, pokud je x \textstyle n–\textstyle m matice obsahující všechny vaše tréninková data, je to vectorized implementace, a výrazy výše uvedené práce také pro výpočetní x_{\rm rot} a \tilde{x} pro celý váš trénink sada vše v jednom jít. Výsledné x_{\rm rot} a \tilde{x} budou mít jeden sloupec odpovídající každému příkladu tréninku.

Pro výpočet PCA bělený data \textstyle x_{\rm PCAwhite},

 xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

Od diagonále obsahuje vlastní čísla \textstyle \lambda_i, to se ukázalo být kompaktní způsob výpočtu, \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} současně pro všechny \textstyle jsem.

a Konečně, můžete také vypočítat ZCA bělený data \textstyle x_{\rm ZCAwhite} jako:

 xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;