co je ARIMAX Model?

jaký je model ARIMAX?

Pokud jste četli náš seriál o blog návody na modely pro odhad časové řady dat, které jste již obeznámeni s 3 hlavní přístupy – r autoregresního, klouzavé průměry a integrace.

jaké je společné téma u všech těchto modelů?

spoléhali pouze na jednu proměnnou.

model však může také brát v úvahu více než jen minulé ceny nebo minulé zbytky.“MAX“, přičemž ARMAX je neintegrovaná verze a ARIMAX-její integrovaný ekvivalent.

takže v tomto tutoriálu prozkoumáme, jak vypadají, a ukážeme vám, jak je implementovat do Pythonu krok za krokem.

začneme, Ano?

proč se ARMAX a ARIMAX nazývají “ MAX “ modely?

názvy ARMAX a ARIMAX přicházejí jako rozšíření ARMA a ARIMA. X přidané na konec znamená „exogenní“. Jinými slovy, navrhuje přidat samostatnou jinou vnější proměnnou, která pomůže měřit naši endogenní proměnnou.

ARMAX a ARIMAX Model Rovnice:

Protože jediný rozdíl mezi ARMAX a ARIMAX je, že jedna je integrovaná a druhá není, můžeme zkoumat jeden z nich, a pak upozornit, jak druhé by se lišily.

prozkoumali jsme integrovaný model v našem posledním článku blogu (ARIMA), takže se podívejme, jak vypadá rovnice ARIMAX.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt,

samozřejmě, že rovnice pro ARMAX by být stejný, jen by jsme použít skutečné proměnné, řekněme P, namísto jeho delta.

Pt=c+ßX+ϕ1 Pt-1+ θ1 ϵt-1 +ϵt,

poškodí ARIMAX Rovnice:

můžeme si ARMAX jako zvláštní případ ARIMAX, kde cílem integrace je 0.

takže pro zbytek tutoriálu se zaměříme na ARIMAX.

a začneme rozdělením různých částí v něm. Pro začátek, Pt a Pt-1 představují hodnoty v aktuálním období a 1 před obdobím.

podobně, ϵt a ϵt-1 jsou chybové výrazy pro stejná dvě období. A, samozřejmě, c je jen základní konstantní faktor.

dva parametry, ϕ1 a θ1, vyjadřují, jaké části hodnoty Pt-1 a error ϵt-1 poslední období jsou relevantní při odhadu aktuálního.

nyní jsou dva nové přírůstky modelu “ X “ a jeho koeficient β. Stejně jako ϕ, β je koeficient, který bude odhadnut na základě výběru modelu a dat. Ale co X?

co je exogenní proměnná?

no, X je exogenní proměnná a může to být libovolná proměnná, která nás zajímá.

může se jednat o časově proměnlivé měření, jako je míra inflace nebo cena jiného indexu. Nebo kategorická proměnná oddělující různé dny v týdnu. Může to být také Booleovské účtování zvláštních svátečních období. Nakonec může znamenat kombinaci několika různých vnějších faktorů.

myšlenka je, že to může být jakákoli jiná proměnná nebo proměnné, které mohou ovlivnit ceny, pokud máme k dispozici data.

takové vnější faktory jsou v naší regresi známé jako exogenní proměnné. Jejich hodnoty používáme k predikci a vysvětlení toho, co nás zajímá, což jsou v našem případě běžné ceny.

jak implementovat modely ARMAX a ARIMAX v Pythonu?

balíček statsmodels přichází s metodou zvanou ARIMA, která je plně schopna zpracovat takové další vstupy.

začneme zadáním charakteristik modelu a pořadí modelu:

poté, co jsme to udělali, musíme také zadat exogenní argument nazvaný „exog“.

na hodnotu, kterou chcete předat, musí být pole nějakého druhu, protože chceme mít hodnoty spojené s každou dobu.

můžeme například použít s&p jako tuto exogenní proměnnou, protože je již máme v našich datech.

nyní jsme připraveni přizpůsobit model ARIMAX (1,1,1).

nezapomeňte pojmenovat proměnnou modelu způsobem, který ji odlišuje od podobných modelů. V tomto případě jsme se rozhodli udělat to přidáním „X, spx“ na konci označuje, že exogeneous proměnná je Y&P

Pak, jak je vidět z úryvků, jsme se nastavit to rovná ARIMA metoda jako předtím, sečteme čas-série, a cílem, jak jsme zvyklí. Nakonec mezi nimi nastavíme argument“ exog „rovný“ DF SPX“, který označuje s&P.

Když jsme vešly tento model a tisknout své souhrnné tabulce, budeme vidět, že jsme se další řádek S&P cen.

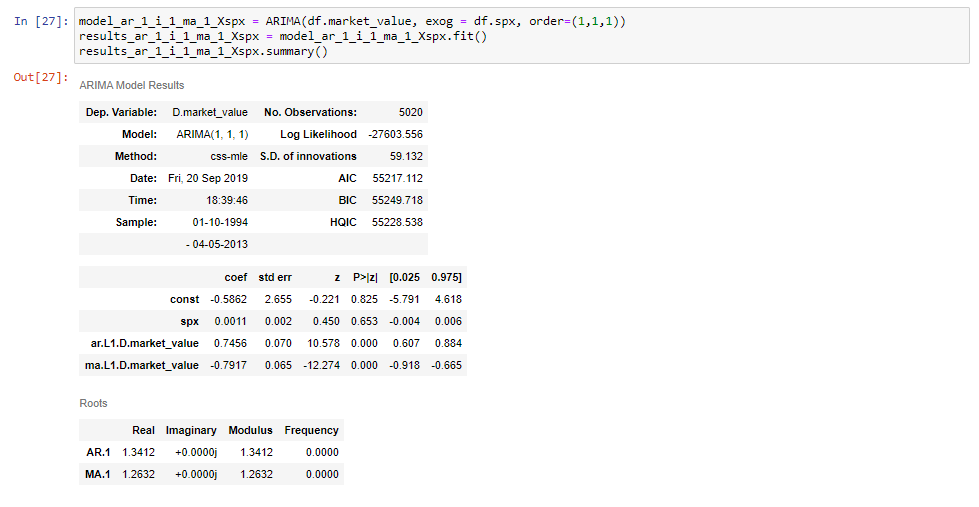
a to je vše, co je k tomu!

úspěšně jsme viděli, jak implementovat model ARIMAX v Pythonu.

Pokud se chcete dozvědět více o ARIMAX a dalších modelech časových řad v Pythonu, nezapomeňte se podívat na naše podrobné výukové programy Python. Pokud jste v Pythonu nováčkem a jste nadšeni, že se dozvíte více, tento komplexní článek o učení programování Pythonu vás provede celou cestou od instalace, přes IDE Pythonu, Knihovny a rámce, až po nejlepší kariérní cesty Pythonu a pracovní výhled.

jste připraveni udělat další krok k kariéře v oblasti datové vědy?

podívejte se na kompletní Data Science Program dnes. Začněte se základy s našimi statistikami, Matematika, a Excel kurzy. Vybudovat krok za krokem zkušenosti s SQL, Python, R, Power BI a Tableau. A upgradujte svou sadu dovedností pomocí strojového učení, hlubokého učení, modelování úvěrových rizik, analýzy časových řad a analýzy zákazníků v Pythonu. Stále si nejste jisti, zda chcete svůj zájem o vědu o datech proměnit v kariéru? Můžete si prohlédnout osnovy nebo se zaregistrovat na 15 hodin začátečníka až po pokročilý videoobsah zdarma kliknutím na tlačítko níže.