
Umělé Neuronové Sítě (ANN) je vyroben z mnoha vzájemně propojených neuronů.
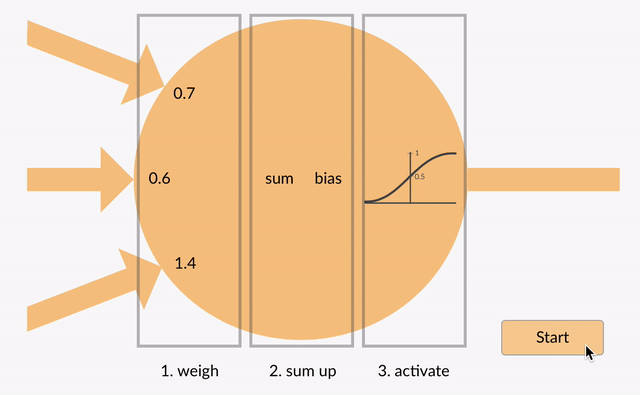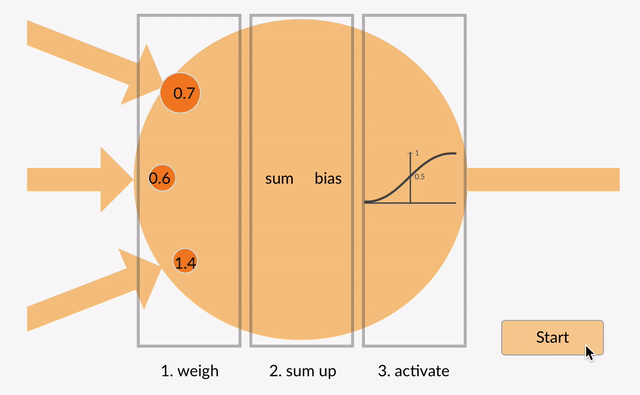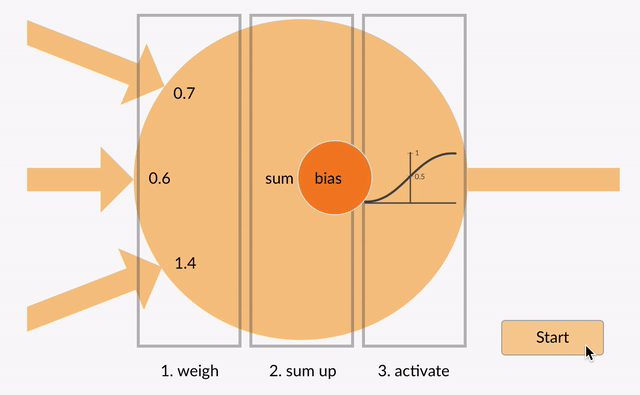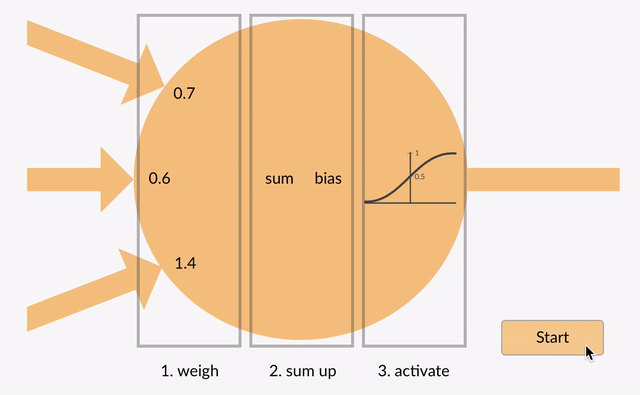
Každý neuron má čísla s plovoucí desetinnou čárkou (např. 1.0, 0.5, -1.0) a násobí je některými jinými čísly s pohyblivou řádovou čárkou (např. 0,7, 0,6, 1,4) známými jako váhy (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Váhy fungují jako mechanismus, který se zaměřuje na určité vstupy nebo je ignoruje.

vážené vstupy pak se sečtou dohromady (např. 0.7 + 0.3 + -1.4 = -0.4) spolu s hodnotou zkreslení (např. -0,4 + -0,1 = -0,5).
součtová hodnota (x) je nyní transformována na výstupní hodnotu (y) podle aktivační funkce neuronu (y = f(x)). Některé populární aktivačních funkcí jsou uvedeny níže:

např. -0.5 → -0.05 pokud budeme používat Děravý Opraveny Lineární Jednotky (Děravé ReLU) aktivace funkce: y = f(x) = f(-0.5) = max(0.1*-0.5, -0.5) = max(-0.05, -0.5) = -0.05
výstupní hodnota neuronu (např. -0,05) je často vstup pro jiný neuron.
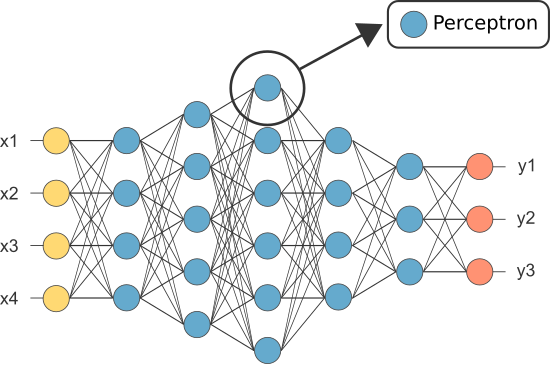
Nicméně, jeden z prvních ANNs byl známý jako perceptron a to se skládala z pouze jeden neuron.

výstup perceptron je (pouze) neuron se chová jako konečné předpovědi.

Umožňuje kód vlastní Perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Poznámka: jsme nejsou zahrnuty žádné algoritmus učení v našem příkladu výše jsme se pokrýt algoritmy učení v jiném tutoriálu)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

tak proč potřebujeme tolik neuronů v ANN, pokud některý postačí (jako klasifikátor)?

Bohužel, jednotlivé neurony jsou schopni klasifikovat lineárně separabilní data.

Nicméně, tím, že kombinuje neurony spolu, jsme v podstatě zkombinovali své rozhodnutí hranice. Proto, ANN složená z mnoha neuronů je schopna se naučit složité, nelineární rozhodovací hranice.

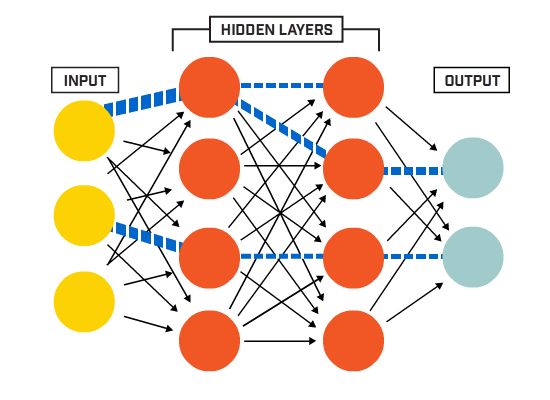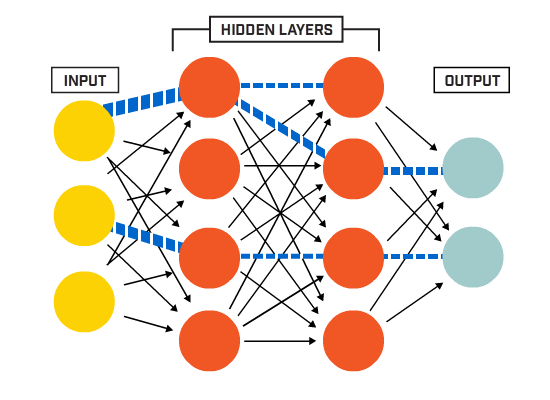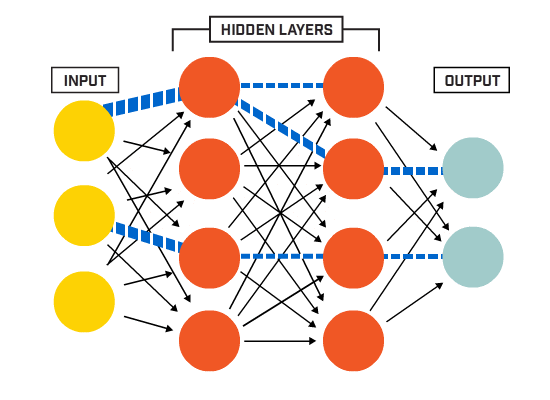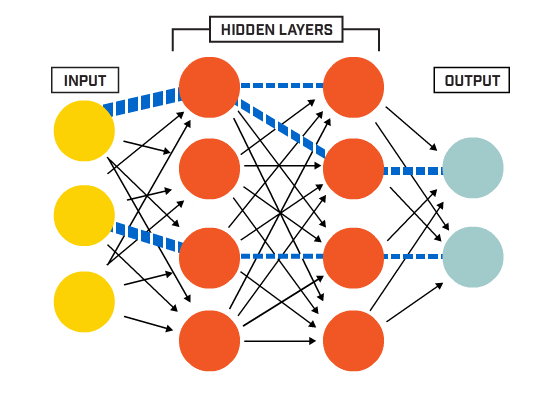
Neurony jsou spojeny dohromady podle konkrétní síťové architektury. Ačkoli existují různé architektury, téměř všechny obsahují vrstvy. (Pozn .: Neurony ve stejné vrstvě nepřipojujte jedna s druhou)
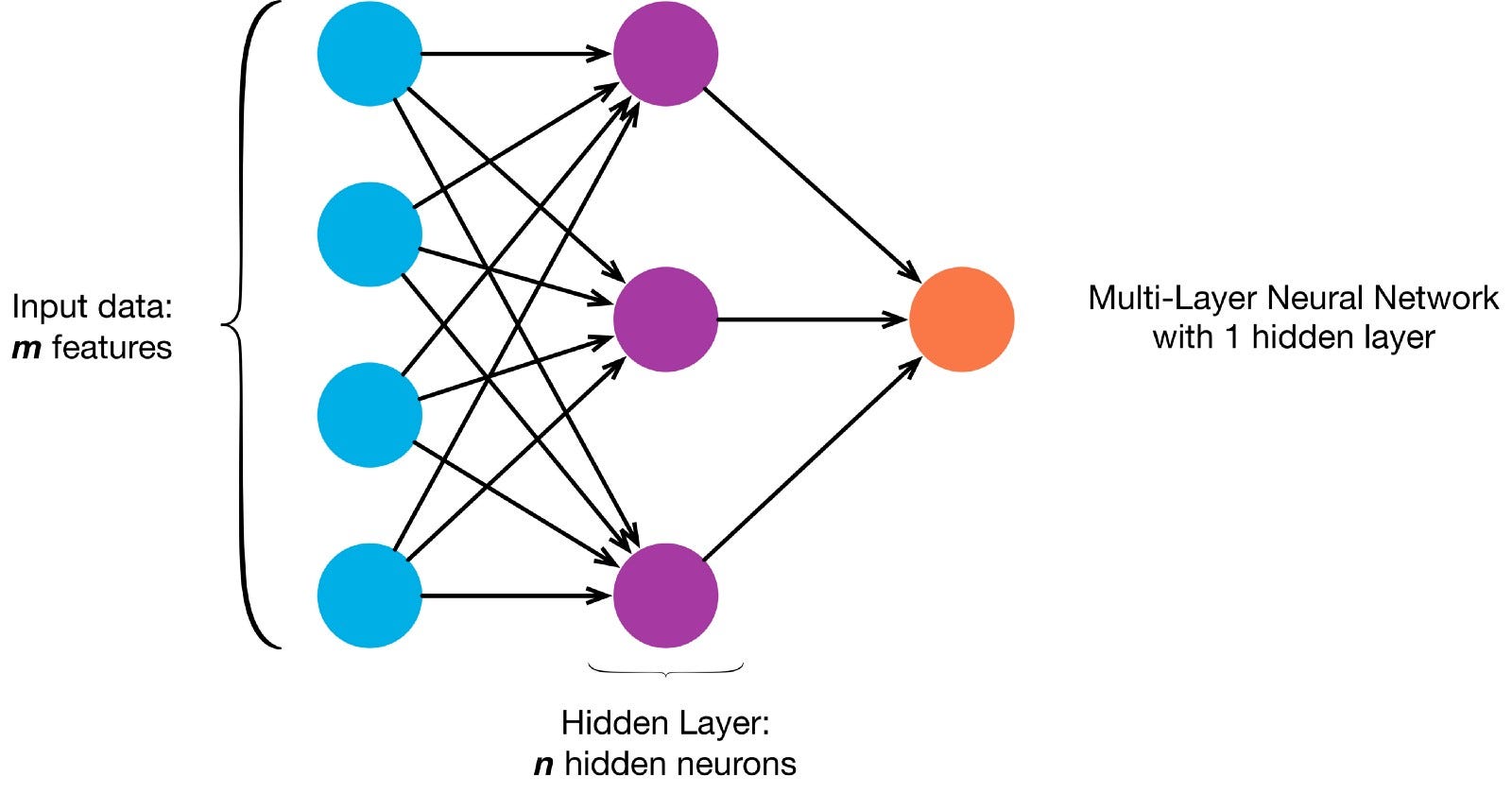
Tam je obvykle vstupní vrstva (obsahující počet neuronů roven počtu vstupních prvků v datové), výstupní vrstva (obsahující počet neuronů odpovídá počtu tříd) a skryté vrstvy (obsahující libovolný počet neuronů).

Tam může být více než jedna skrytá vrstva, aby se neuronová síť se dozvědět více komplexní rozhodovací hranice (neurální síť s více než jednou skrytou vrstvou je považován za hluboké neuronové sítě).
umožňuje vytvořit hluboký NN malovat tento obrázek:

Umožňuje stáhnout obrázek a nahrát své pixelů do pole
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Nyní učí naše ANN malovat je pod dohledem, učení, úkol, tak musíme vytvořit označeny školení set (Naše data školení bude mít vstupy a očekávané výstupy etikety pro každý vstup). Tréninkové vstupy budou mít 2 hodnoty (souřadnice X, y každého pixelu).
vzhledem k jednoduchosti obrazu bychom k tomuto problému mohli přistoupit jedním ze dvou způsobů. Klasifikační problém (kde neuronová síť předpovídá, zda pixel patří do třídy“ modrá „nebo“ šedá“, vzhledem k jeho souřadnicím xy) nebo regresní problém (kde neuronová síť předpovídá hodnoty RGB pro pixel vzhledem k jeho souřadnicím).
Pokud se jedná o regresní problém: tréninkové výstupy budou mít 3 hodnoty (normalizované hodnoty r, g, b pro každý pixel). – Umožňuje používat tuto metodu pro tuto chvíli.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Nyní umožňuje vytvořit naše ANN:

- mělo by To mít 2 neurony ve vstupní vrstvě (protože tam jsou 2 hodnoty vzít v: x & y souřadnice).
- měl by mít 3 neurony ve výstupní vrstvě (protože existují 3 hodnoty, které se mají naučit: r, g, b).
- počet skrytých vrstev a počet neuronů v každé skryté vrstvě jsou dvě hyperparameters experimentovat s (stejně jako počet epoch budeme trénovat to, aktivační funkce, atd.) — budu používat 10 skryté vrstvy s 100 neuronů v každé skryté vrstvě (takže to hluboké neuronové sítě)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
vyškolený sítě mohou nyní předpovídají, normalizované hodnoty rgb pro všechny souřadnice (např. x,y = 1,1).
ann.predict(])
array(])
umožňuje použít ANN předpovědět hodnoty rgb pro každý souřadnic a umožňuje zobrazit předpokládané hodnoty rgb pro celý obraz vidět, jak dobře to udělal (kvalitativně — necháme hodnotící metriky pro další tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Zkuste změnit hyperparameters získat lepší výsledky.
Pokud se místo toho jedná o regresní problém, budeme to považovat za klasifikační problém, pak výcvik výstupy bude mít 2 hodnoty (pravděpodobnosti, že pixel patřící do každé ze dvou tříd: „blue“ a „šedá“)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
můžeme obnovit naše ANN jako binární klasifikátor s 2 neurony ve vstupní vrstvě, 2 neurony ve výstupní vrstvě a 100 neuronů ve skryté vrstvě (s 10 skryté vrstvy)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
nyní můžeme použít vyškoleni ANN předvídat třídy, která každý pixel patří (0: „šedá“ nebo 1: „modrá“). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: „grey“)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

