bez Dozoru Bayesian Závěr (snížení rozměrů a odkrývat funkce)
Low-level funkce detekce pomocí hrany

a Konečně, v okamžiku, kdy jste všichni čekali, další v naší dozoru Bayesian závěr série: Naše (ne tak) hluboký ponor do Sobel Operator.
skutečně magický algoritmus detekce hran, umožňuje extrakci prvků na nízké úrovni a redukci dimenzionality, což v podstatě snižuje šum v obraze. To bylo zvláště užitečné v aplikacích rozpoznávání obličeje.
1968 love child of Irwin Sobel a Gary Feldman (Stanford Artificial Intelligence Laboratory), tento algoritmus byl inspirací mnoha moderních technik detekce hran. Konvolvováním dvou protichůdných jader nebo masek na daný obrázek (např. viz níže-vlevo) (každý schopný detekovat vodorovné nebo svislé hrany), můžeme vytvořit méně hlučné, vyhlazené zobrazení(viz níže-vpravo).
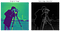
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel hodnoty (obvykle jas) rozlišováním rozdílu mezi každým pixelem (kotevní pixel) a jeho okolními pixely (v podstatě aproximace derivace obrazu).
výsledkem je vyhlazení původního obrazu a vytvoření výstupu s nižší dimenzí, kde lze jasněji vidět geometrické rysy nízké úrovně. Tyto výstupy pak mohou být použity jako vstupy do složitějších klasifikačních algoritmů, nebo jako příklady použity pro bez dozoru pravděpodobnostní shlukování pomocí Kullback-Leibler Divergence (KLD) (jak je vidět v mém nedávném blogu na LBP).
generování výstupů nižší dimenze vyžaduje, abychom převzali derivaci obrazu. Nejprve vypočítáme derivát ve směru x I y. Vytvoříme dvě jádra 3×3 (viz matice), s nul podél středu příslušné osy, dvojky ve středu čtverce kolmo do centrální nula a jedniček v každém z rohů. Každá z nenulových hodnot by měla být kladná nahoře / vpravo od nul (v závislosti na ose) a záporná na jejich odpovídající straně. Tato jádra se jmenují Gx a Gy.
zobrazí se ve formátu:
Tato jádra se pak convolve nad naší image, umístění centrální pixel každého jádra, přes každý pixel v obrazu. Násobení matice používáme k výpočtu hodnoty intenzity nového odpovídajícího pixelu ve výstupním obrazu pro každé jádro. Proto skončíme dvěma výstupními obrazy(jeden pro každý kartézský směr).
cílem je najít rozdíl/změnu mezi pixelem v obraze a všemi pixely v matici přechodu (jádro) (Gx a Gy). Matematičtěji to lze vyjádřit jako.
boční poznámka:
technicky nic nespojujeme. I když říkáme ‚závitů v AI a machine learning kruhy, konvoluce by znamenalo překlopení původního obrazu. Matematicky řečeno, když odkazujeme na konvoluce, skutečně počítáme křížovou korelaci mezi každou 3×3 oblastí vstupu a maskou pro každý pixel. Výstupní obraz je celková kovariance mezi maskou a vstupem. Takto jsou detekovány hrany.
Zpět na naše Sobel vysvětlení…
vypočtené hodnoty pro každý násobení matic mezi maskou a 3×3 část vstupu jsou shrnul závěrečnou hodnotu pixelu ve výstupním obraze. Tím se vytvoří nový obrázek, který obsahuje informace o přítomnosti svislých a vodorovných hran přítomných v původním obrázku. Jedná se o geometrický rys reprezentace původního obrazu. Dále, protože je zaručeno, že tento operátor bude produkovat stejný výstup pokaždé, tato technika umožňuje stabilní detekci hran pro úlohy segmentace obrazu.
Z těchto výstupů, můžeme vypočítat, jak gradientu a směr gradientu (pomocí arkustangens provozovatele) v daném pixelu (x,y):
Z toho můžeme zjistit, že ty pixely s velkým veličin jsou více pravděpodobné, že být hranu v obrázku, zatímco směru nás informuje o hraně orientace (i když směr není potřeba pro generování náš výstup).
jednoduchá implementace:
Zde je jednoduchý provádění Sobel operátor v pythonu (pomocí NumPy), aby vám pocit, pro proces (pro všechny začínající programátory venku).
Toto je implementace python varianta Wikipedie pseudokódu příklad, jehož cílem je ukázat, jak může provedení tohoto algoritmu, a zároveň demonstrovat jednotlivé kroky v procesu.
proč se staráme?
ačkoli gradientní aproximace vytvořená tímto operátorem je relativně hrubá, poskytuje extrémně výpočetně efektivní metodu výpočtu hran, rohů a dalších geometrických vlastností obrazů. Na druhé straně to vydláždilo cestu pro řadu technik redukce dimenzionality a extrakce funkcí, jako jsou místní binární vzory (viz můj další blog pro více informací o této technice).
spoléhání se na výhradně geometrické rysy riskuje ztrátu důležitých informací během kódování našich dat, ale kompromis je to, co umožňuje rychlé předzpracování dat a zase rychlé školení. Proto je tato technika zvláště užitečná ve scénářích, kde lze texturu a geometrické rysy považovat za velmi důležité při definování vstupu. To je důvod, proč lze rozpoznávání obličeje dokončit s relativně vysokou mírou přesnosti pomocí operátora Sobel. Tato technika však nemusí být nejlepší volbou, pokud se snažíte klasifikovat nebo seskupovat vstupy, které používají barvu jako svůj hlavní rozlišovací faktor.
Tato metoda je velmi efektivní pro získání low-dimenzionální reprezentace geometrických funkcí a výborným výchozím bodem pro dimenzionality a redukce šumu, před použitím jiné klasifikátory nebo pro použití v Bayesovské inference metody.