Pochopení Hluboké Zbytkové Sítě

Hluboké reziduální sítě (ResNet) vzal hluboké učení svět bouří, když Microsoft Research vydala Hluboké Zbytkové Učení pro Rozpoznávání Obrazu. Tyto sítě vedl k 1.-místo vítězné příspěvky ve všech pěti hlavních kolejích z ImageNet a COCO 2015 soutěže, která se týkala klasifikace obrazu, detekce objektů, a sémantické segmentace. Robustnost Resnetů byla od té doby prokázána různými úkoly vizuálního rozpoznávání a nevizuálními úkoly zahrnujícími řeč a jazyk. ResNet jsem použil kromě jiných modelů hlubokého učení v mém Disertačním výzkumu.

Tento příspěvek bude shrnout tři dokumenty níže, který jsou psaný nebo co-napsaný ResNet je vynálezce Kaiming On, protože věřím, že původní dokumenty, poskytují nejvíce intuitivní a podrobné vysvětlení model/sítě. Doufejme, že tento příspěvek vám pomůže lépe porozumět podstatě zbytkových sítí.

• Hluboké Zbytkové Učení pro Rozpoznávání Obrazu
• Identita mapování v Hluboké Zbytkové Sítě
• Souhrnné Reziduální Transformace pro Hluboké Neuronové Sítě

Intuice na Hluboké Reziduální Sítě (stackoverflow ref)

zbytkový blok je zobrazen jako následující:

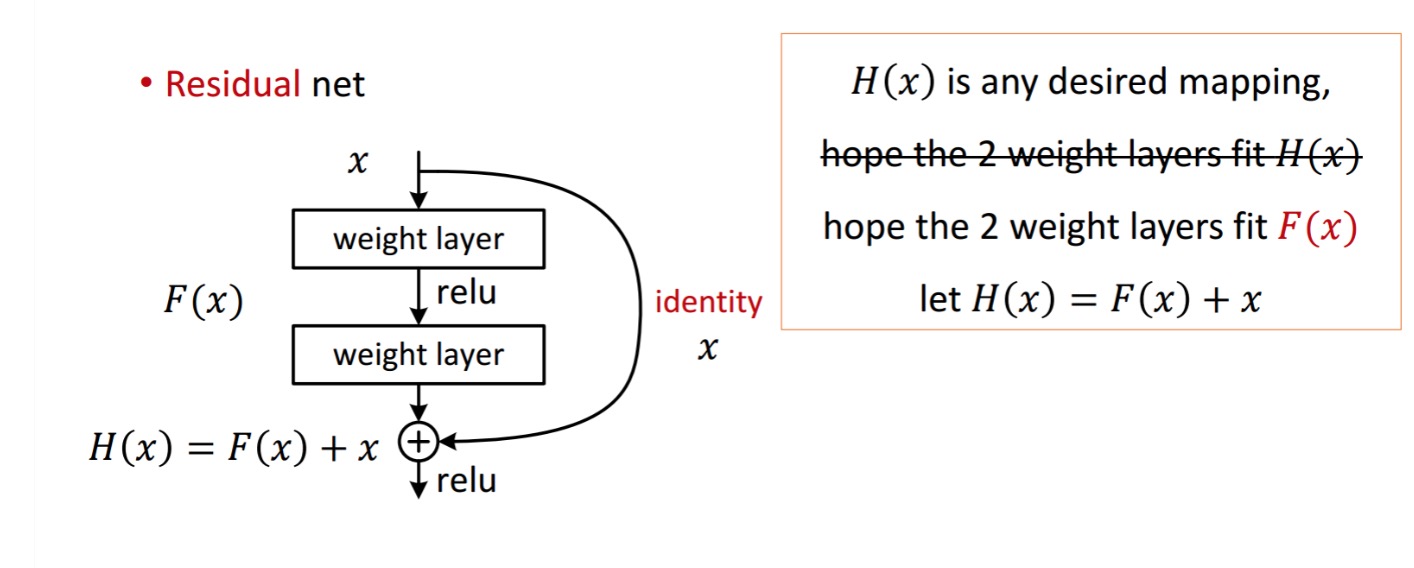
Tak zbytkové jednotky je znázorněno získává zpracováním s dvěma hmotnosti vrstvy. Pak se přidá k získání . Nyní předpokládejme, že je to váš ideální předpovězený výstup, který odpovídá vaší pozemní pravdě. Vzhledem k tomu, že získání požadovaného závisí na získání dokonalého . To znamená, že dvě hmotnostní vrstvy ve zbytkové jednotce by měly být skutečně schopny produkovat požadované,pak je zaručeno získání ideálu.

se získá následujícím způsobem.

se získá následujícím způsobem.

autoři předpokládají, že zbytkové mapování (tj. ) může být jednodušší optimalizovat než. Pro ilustraci jednoduchým příkladem předpokládejme, že ideál . Pro přímé mapování by pak bylo obtížné naučit se mapování identity, protože existuje hromada nelineárních vrstev následovně.

takže aproximovat mapování identity se všemi těmito váhami a Relusem uprostřed by bylo obtížné.

Nyní, pokud definujeme požadované mapování, pak stačí získat následovně.

dosažení výše uvedeného je snadné. Stačí nastavit libovolnou hmotnost na nulu a dostanete nulový výstup. Přidat zpět a dostanete požadované mapování.

Hluboké Zbytkové Učení pro Rozpoznávání Obrazu

Když se hlouběji sítí začíná sbližují, degradace problém byl vystaven: s network hloubky zvyšuje, přesnost dostane nasycené a pak se rychle rozkládá.

Ponižující Vidět v Akci:

vezměme si mělkou síť a její hlubší protějšek přidáním více vrstev.

Nejhorší scénář: Hlubší model je brzy vrstvy mohou být nahrazeny s mělkou síť a zbývající vrstvy se může jen jednat jako funkce identita (Vstup rovná výstupu).

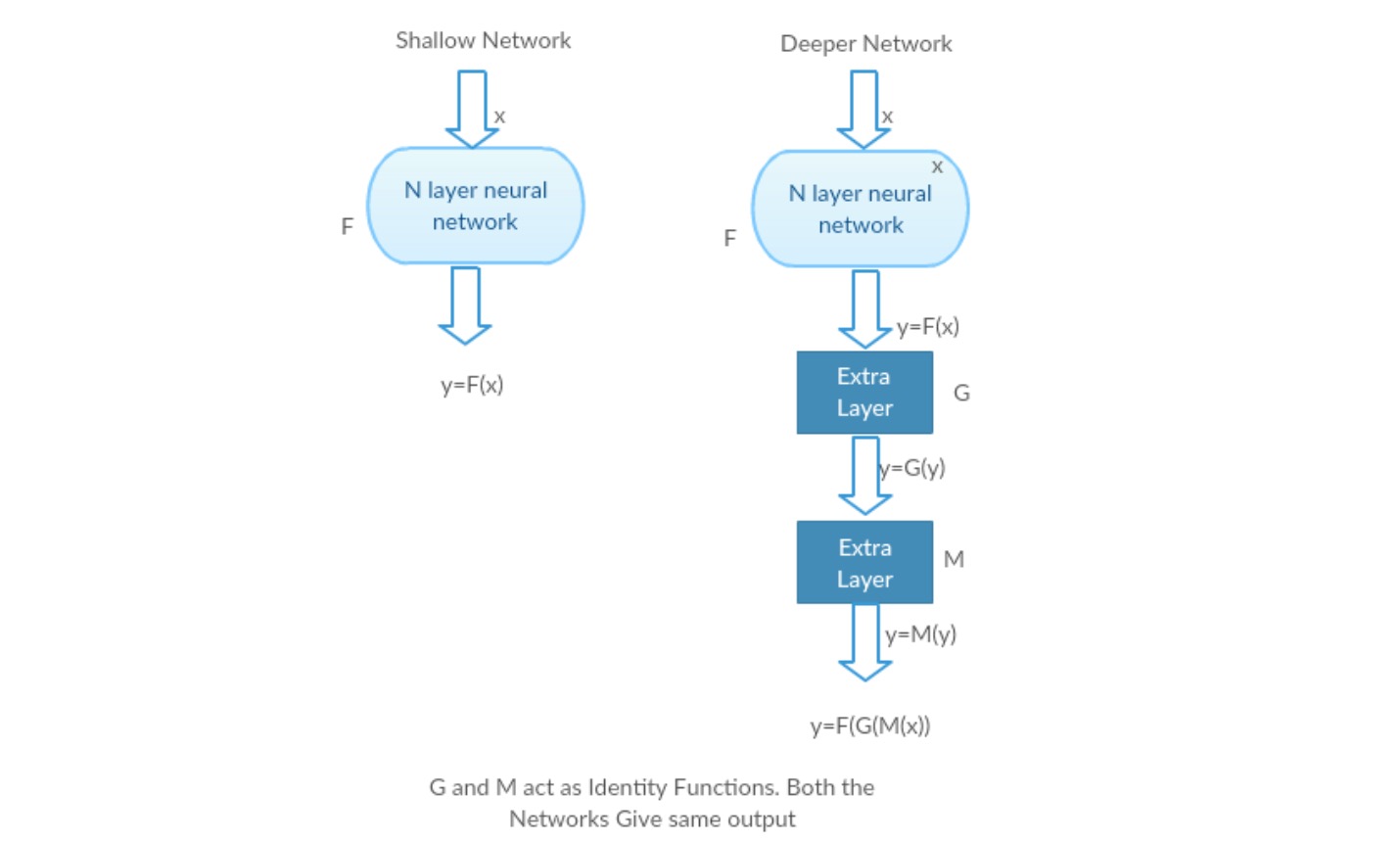
Obohacující scénář: V hlubší síť další vrstvy lépe aproximuje mapování, než je mělčí pult součástí a snižuje chybu tím, že značný prostor.

Experiment: V nejhorším případě by měla mít stejnou přesnost jak mělká síť, tak její hlubší varianta. V případě odměňování scénář, hlubší model by měl poskytnout lepší přesnost, než je to mělčí čítač část. Experimenty s našimi současnými řešiteli však ukazují, že hlubší modely nefungují dobře. Takže použití hlubších sítí degraduje výkon modelu. Tyto práce se snaží tento problém vyřešit pomocí hlubokého zbytkového rámce učení.

jak řešit?

namísto učení přímé mapování s funkcí (několik naskládaných nelineárních vrstev). Definujme zbytkovou funkci pomocí , na kterou lze přeformulovat, kde a představuje naskládané nelineární vrstvy a identitní funkci(input=output).

autorova hypotéza je, že je snadné optimalizovat zbytkové funkce mapování než optimalizovat původní, neodkazované mapování .

intuice za zbytkovými bloky:

Vezměme si mapování identity jako příklad (např.). Pokud je mapování identity optimální, můžeme jednoduše tlačit zbytky na nulu (), než aby se vešly mapování identity () stohem nelineárních vrstev. V jednoduchém jazyce je velmi snadné přijít s řešením, jako spíše než pomocí zásobníku nelineárních vrstev cnn jako funkce(Přemýšlejte o tom). Takže tato funkce je to, co autoři nazývali zbytkovou funkcí.

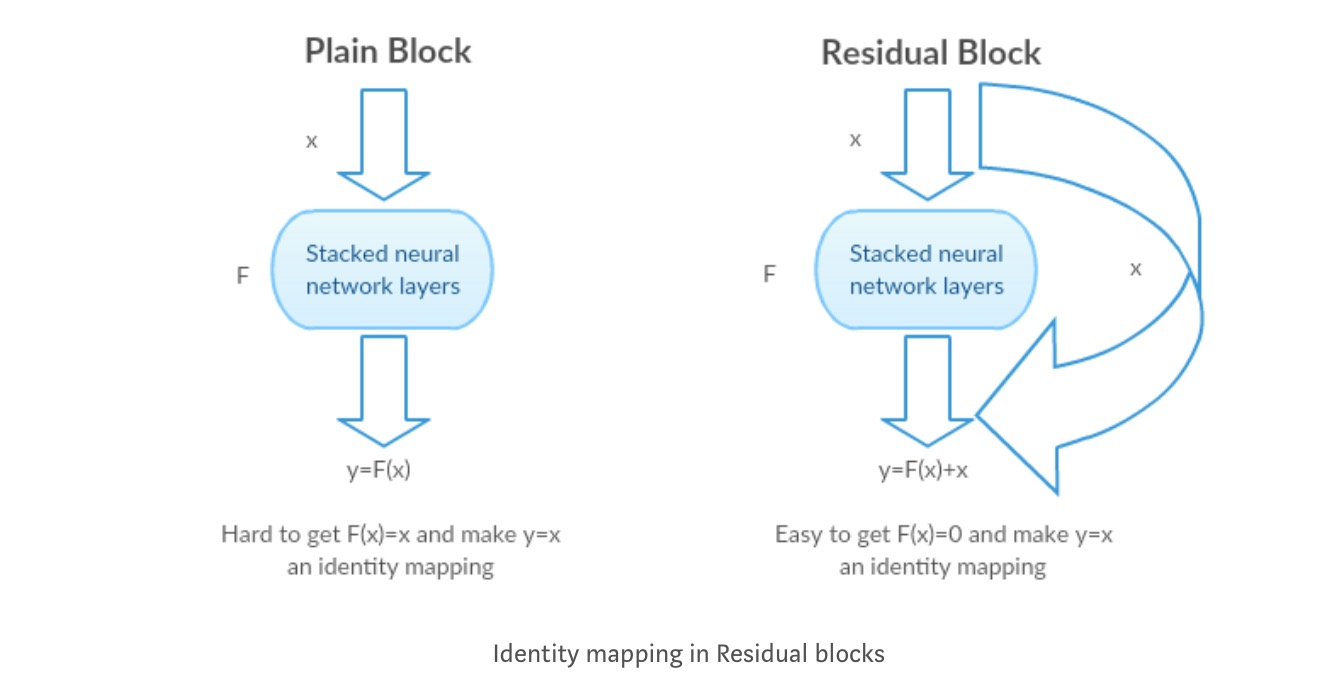
autoři provedli několik testů pro testování jejich hypotézu. Podívejme se nyní na každou z nich.

Testovací případy:

Vezměte obyčejný sítě (VGG druh 18 vrstvu network) (Síť-1) a hlubší varianta (34-vrstva, Síť-2) a přidat Zbytkové vrstvy do Sítě-2 (34 vrstva s reziduální připojení, Sítě-3).

navrhování sítě:

1. používejte většinou 3 * 3 filtry.
2. vzorkování dolů s vrstvami CNN s krokem 2.
3. Globální průměrná sdružovací vrstva a 1000-way plně připojená vrstva s Softmax na konci.

Existují dva druhy zbytkových připojení:

I identitu zkratky (), může být přímo použit, když je vstup () a výstup () mají stejné rozměry.

II. Když se však změní kóty, A) zástupce stále provádí mapování identity, s možností nulové položky čalouněný s vyšší dimenze. B) projekce zkratka se používá, aby odpovídaly rozměr (provádí 1*1 conv) pomocí tohoto vzorce,

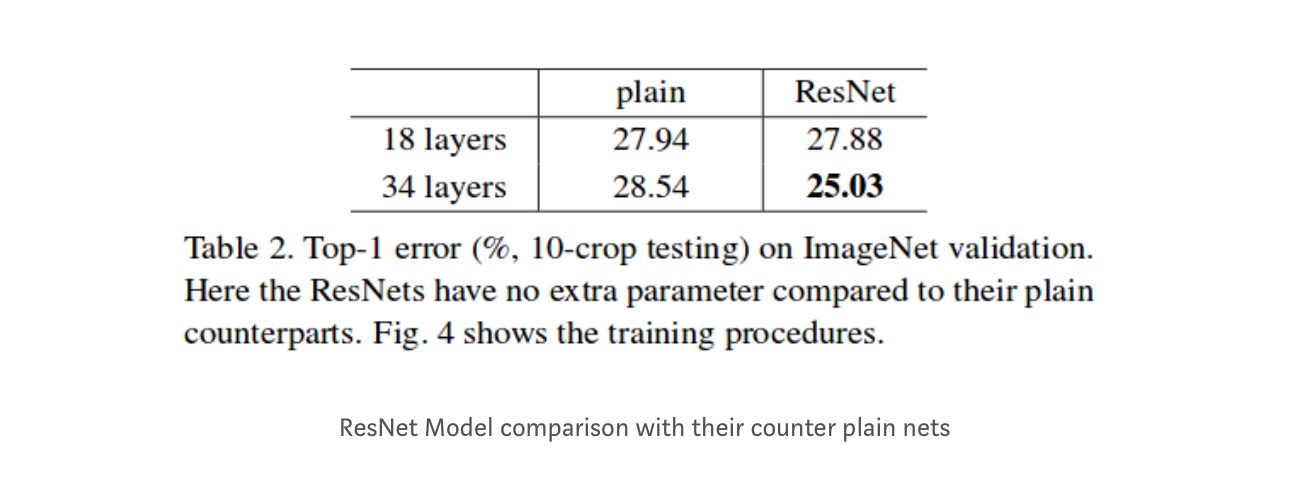
Výsledky

I když 18 vrstva sítě je právě podprostor ve 34 vrstvy sítě, je stále provádí lépe. ResNet překonává značné rozpětí v případě, že síť je hlubší,

Hlubší studie

Navíc, další sítě jsou studovány:

Každý ResNet blok je buď 2 vrstvy hluboké (Používá se v malých sítích, jako je ResNet 18, 34) nebo 3 vrstvy hluboké( ResNet 50, 101, 152).

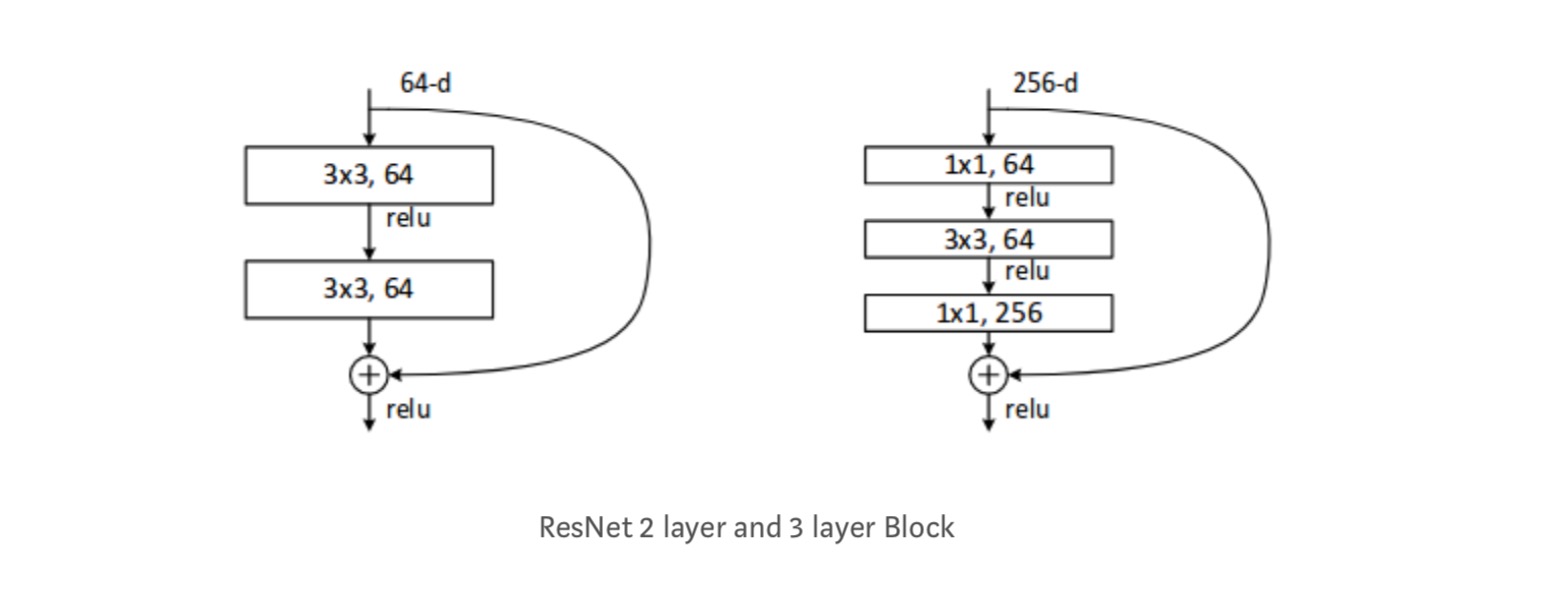
Pozorování

1. ResNet Síť Konverguje rychleji v porovnání s prostý čítač součástí.
2. identita vs projekce shorcuts. Velmi malé přírůstkové zisky pomocí projekčních zkratek (rovnice-2) ve všech vrstvách. Všechny bloky ResNet tedy používají pouze zkratky Identity s zkratkami projekcí, které se používají pouze při změně rozměrů.
3. ResNet-34 dosáhl chyby ověření top-5 o 5.71% lepší než BN-inception a VGG. ResNet-152 dosahuje chyby ověření top-5 4,49%. Soubor 6 modelů s různými hloubkami dosahuje chyby ověření top-5 3, 57%. Vyhrál 1. místo v ILSVRC-2015

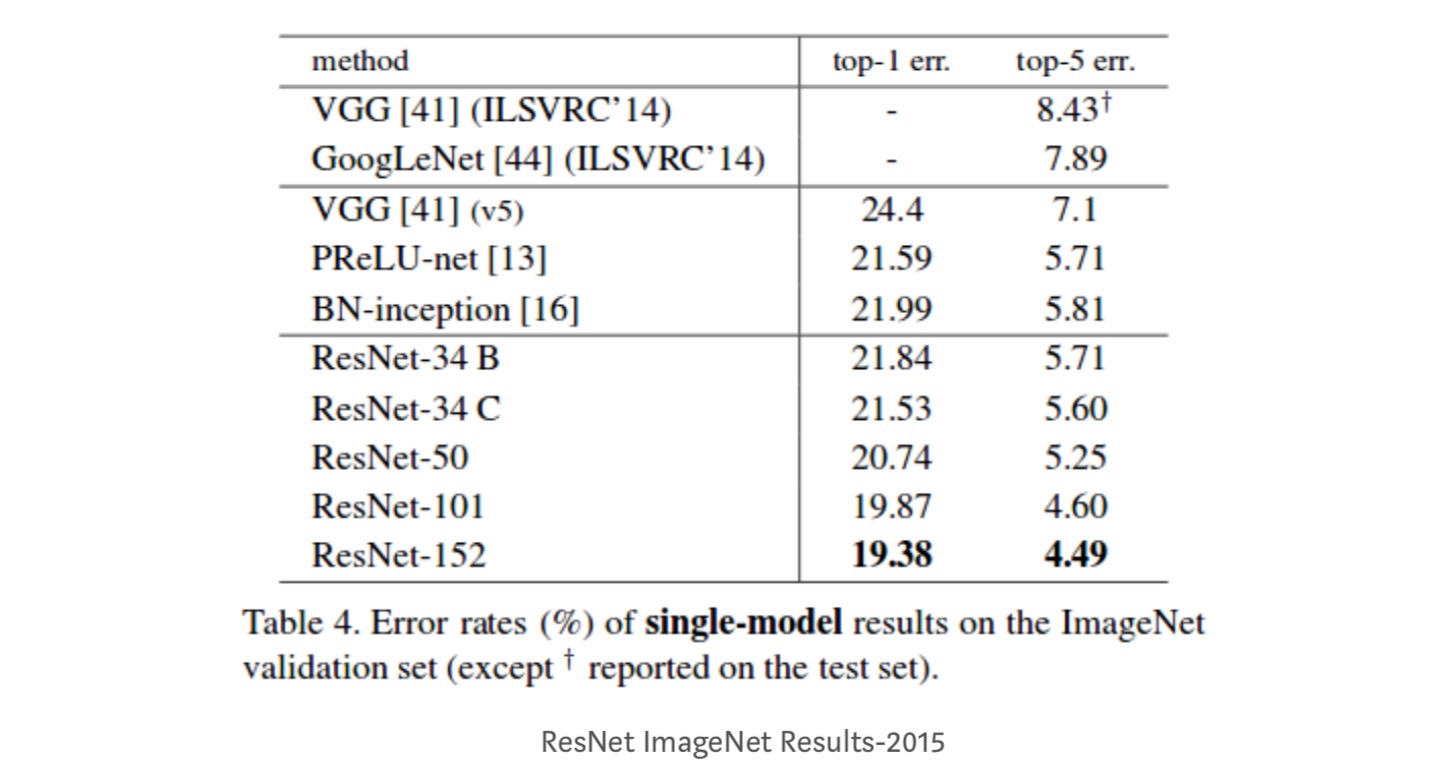
Identity mapování v Hluboké Zbytkové Sítě

Tento papír dává teoretické pochopení toho, proč vanishing gradient problém není přítomen v Reziduální sítě a role přeskočit připojení (skip připojení na mysli vstupní nebo ) nahrazením Identity mapping (x) s různými funkcemi.

Úvod

hluboké zbytkové sítě se skládají z mnoha naskládaných „zbytkových jednotek“. Každá jednotka může být vyjádřena v obecné podobě:

kde a jsou vstupy a výstupy jednotky a je zbytkovou funkcí. V posledním příspěvku, je mapování identity a je funkce ReLU.

hlavní myšlenkou Resnetů je naučit se aditivní zbytkovou funkci s ohledem na, s klíčovou volbou použití mapování identity . To je realizováno připojením spojení pro přeskočení identity („zkratka“).

v tomto článku analyzujeme hluboké zbytkové sítě se zaměřením na vytvoření „přímé“ cesty pro šíření informací-nejen v rámci zbytkové jednotky, ale v celé síti. Naše derivace ukazují, že pokud oba a jsou identitu mapování, signál může být přímo rozšířena, z jedné jednotky do jiných jednotek, v obou dopředu a dozadu přechází. Naše experimenty empiricky ukazují, že trénink obecně se stává jednodušším, když je architektura blíže výše uvedeným dvěma podmínkám.

abychom pochopili roli přeskočení připojení, analyzujeme a porovnáváme různé typy . Zjistili jsme, že mapování identity vybrané v posledním příspěvku dosahuje nejrychlejšího snížení chyb a nejnižší ztráty tréninku ze všech variant, které jsme zkoumali , zatímco přeskočení spojení škálování, brány a 1×1 konvoluce vedou k vyšší ztrátě a chybám tréninku. Tyto experimenty naznačují, že udržování „čisté“ informační cesty je užitečné pro usnadnění optimalizace.

pro vytvoření mapování identity považujeme aktivační funkce (ReLU a BN) za „předběžnou aktivaci“ hmotnostních vrstev, na rozdíl od konvenční moudrosti „postaktivace“. Toto hledisko vede k nové konstrukci zbytkové jednotky, znázorněné na následujícím obrázku. Na základě této jednotky, představujeme konkurenceschopných výsledků na CIFAR-10/100 s 1001-vrstva ResNet, což je mnohem jednodušší trénovat a zobecňuje lepší než původní ResNet. Dále hlásí lepší výsledky na ImageNet pomocí 200-vrstva ResNet, pro které protějšek z posledních papír začne overfit. Tyto výsledky naznačují, že existuje mnoho prostoru pro využití dimenze hloubky sítě, klíč k úspěchu moderního hlubokého učení.

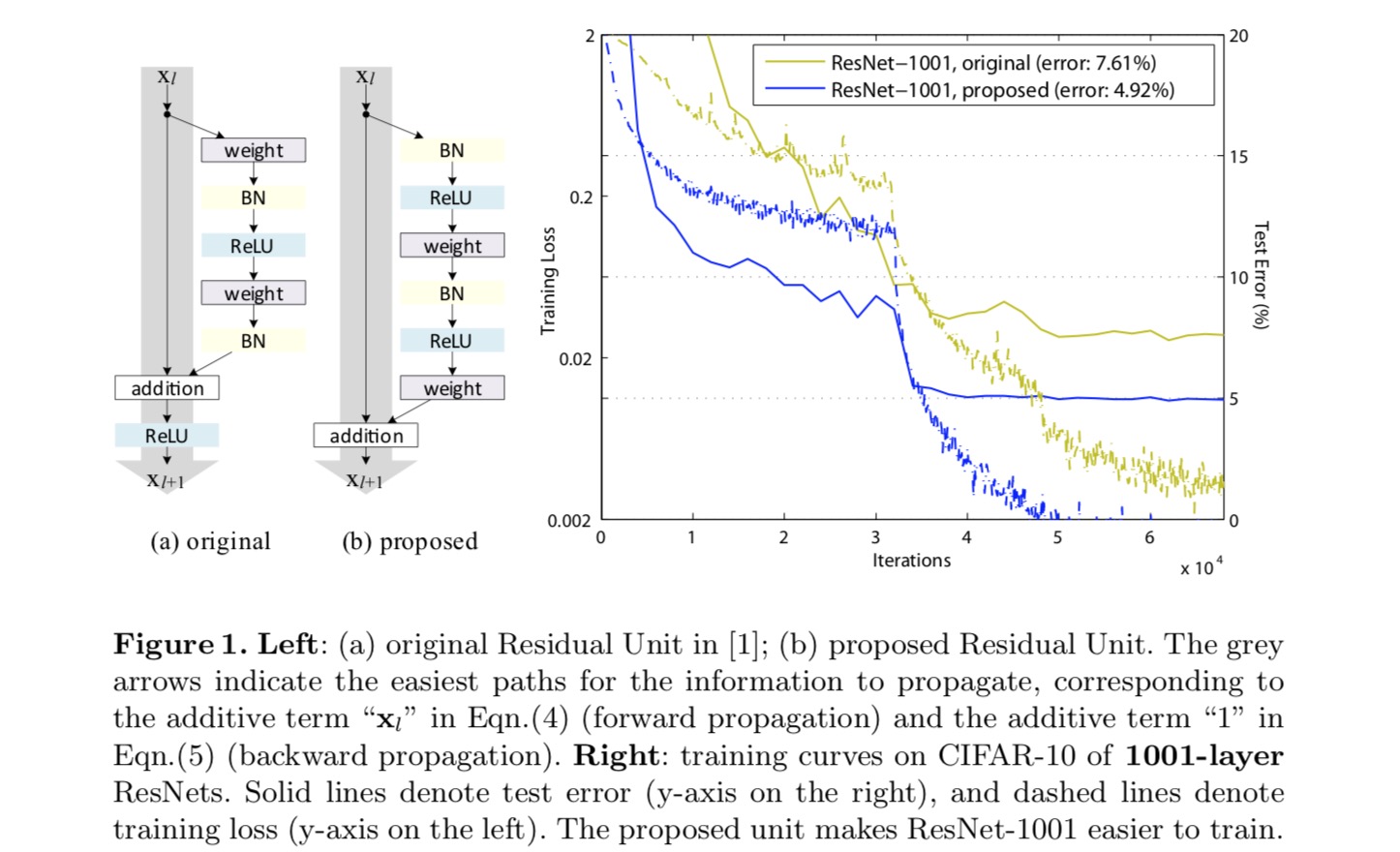
Analýza Hluboké Zbytkové sítě

ResNets vyvinul v posledních papíru jsou modulární architektury, která stack stavební bloky stejné připojení tvar. V tomto článku nazýváme tyto bloky „Zbytkové jednotky“. Původní zbytková jednotka v posledním článku provede následující výpočet:

zde je vstupní funkce do-té Zbytkové jednotky. je sada závaží (a zkreslení) spojené s-tý Zbytkové jednotky, a je počet vrstev ve zbytkové jednotce (je 2 nebo 3 v posledním papíru). označuje zbytkovou funkci, e.g., stoh dvou 3×3 konvolučních vrstev v posledním papíru. Funkce je operace po přidání prvku, a v posledním příspěvku je ReLU. Funkce je nastavena jako mapování identity: .

Pokud je také mapování identity:, můžeme získat:

rekurzivně budeme mít:

pro jakoukoli hlubší jednotku a jakoukoli mělčí jednotku . Tato rovnice vykazuje některé hezkévlastnosti. (1) funkce nějaké hlubší jednotky mohou být reprezentovány jako funkce nějaké mělčí jednotka plus zbytkové funkce ve formě , což naznačuje, že model je v reziduálním módní mezi žádné jednotky a . (2) znakem jakékoli hluboké jednotky je součet výstupů všech předchozích zbytkových funkcí (plus ). To je na rozdíl od „prosté sítě“, kde funkce je řada maticově vektorových produktů, řekněme (ignorování BN A ReLU).

výše uvedená rovnice také vede k pěkným zpětným vlastnostem šíření. Označuje ztrátu funkce jako z řetězu pravidlo backpropagation máme:

výše uvedené rovnice vyplývá, že gradient lze rozložit na dvě aditivní podmínky: termín, který šíří informace přímo, aniž by se týkal jakýchkoli hmotnostních vrstev, a další termín, který se šíří hmotnostními vrstvami. Doplňkové látky období zajišťuje, že informace je přímo šířeny zpět na jakékoliv menší jednotky l. Výše uvedené rovnice také vyplývá, že je nepravděpodobné, že pro gradient být zrušena pro mini-batch, protože obecně termín nemůže být vždy -1 pro všechny vzorky v mini-batch. To znamená, že gradient vrstvy nezmizí, i když jsou váhy libovolně malé.

výše uvedené dvě rovnice naznačují, že signál může být přímo šířen z jakékoli jednotky do jiné, a to jak dopředu, tak dozadu. Základem prvních výše uvedených dvou rovnic jsou dvě mapování identity: (1) spojení identity skip a (2) podmínka, která je mapováním identity.

význam spojení identity přeskočit

uvažujme jednoduchou modifikaci,, prolomit zkratku identity:

kde je modulační skalár (pro jednoduchost stále předpokládáme, že je identita). Rekurzivním použitím této formulace získáme rovnici podobnou výše uvedené:

kde notace absorbuje skaláry do zbytkových funkcí. Podobně máme backpropagaci následující formy:

Na rozdíl od předchozí rovnice je v této rovnici první aditivní termín modulován faktorem . Pro extrémně hluboké sítě ( je velký), pokud pro všechny , tento faktor může být exponenciálně velký; pokud pro všechny , tento faktor může být exponenciálně malé a zmizí, což blokuje backpropagated signál z místní a síly na to, aby průtok hmotnost vrstev. To má za následek potíže s optimalizací, jak ukazují experimenty.

ve výše uvedené analýze je původní spojení identity skip nahrazeno jednoduchým škálováním . Pokud spojení skip představuje složitější transformace (například gating a 1×1 konvoluce), ve výše uvedené rovnici se první člen stává kde je derivace . Tento produkt může také bránit šíření informací a bránit tréninkovému postupu, jak bylo uvedeno v následujících experimentech.

Experimenty na Přeskočit Připojení

experimentovat s 110-vrstva ResNet na CIFAR-10. Tento extrémně hluboký ResNet-110 má 54 dvouvrstvých zbytkových jednotek (skládajících se z 3×3 konvolučních vrstev) a je náročný na optimalizaci. Experimentují se různé typy přeskočení. Viz následující obrázek:

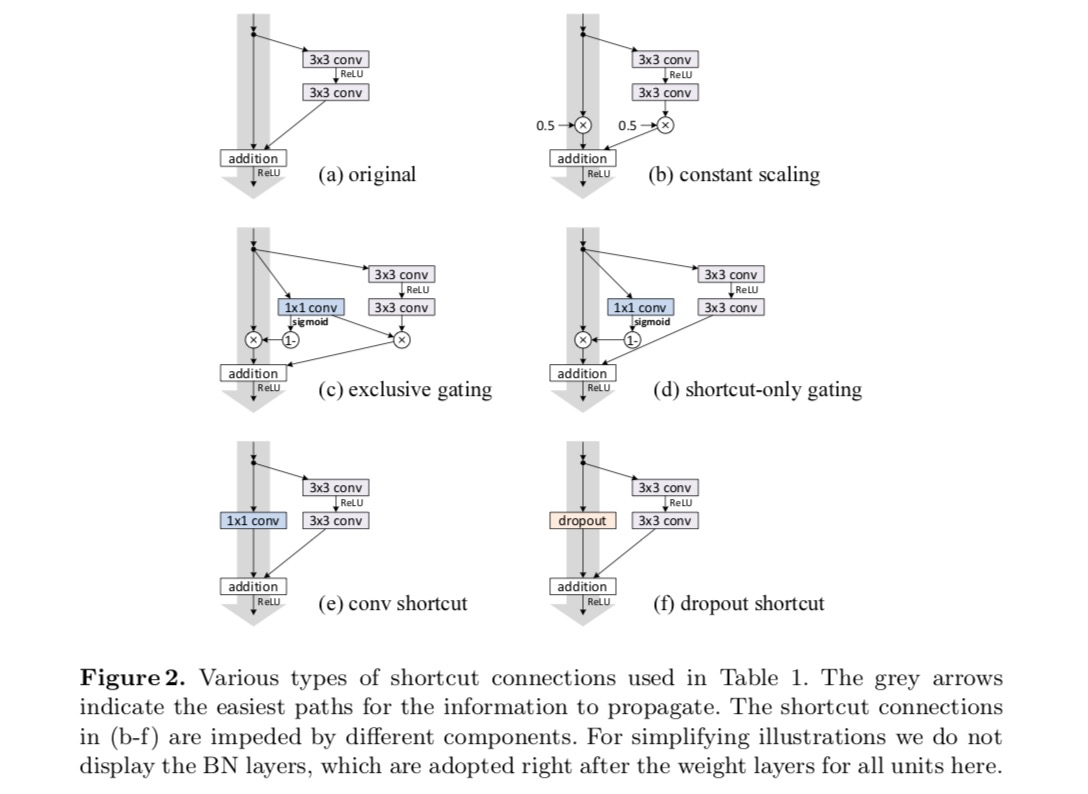
klasifikace výsledky jsou zobrazeny v následující tabulce:

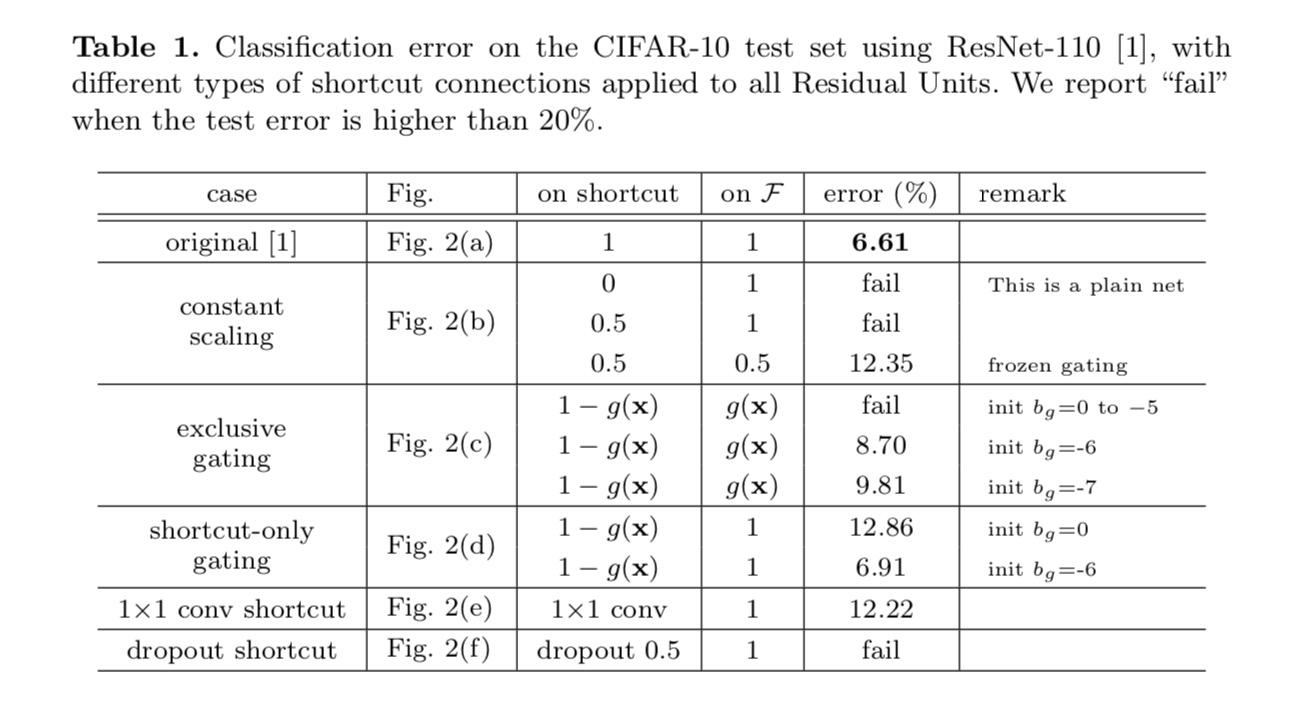
Jak je uvedeno na šedé šipky na obrázku výše, místní spoje jsou nejvíce přímé cesty pro informace šířit. Multiplikativní manipulace (škálování, bránění, 1×1 konvoluce a výpadek) na zkratkách mohou bránit šíření informací a vést k problémům s optimalizací.

je pozoruhodné, že vtokové a 1×1 konvoluční zkratky zavést více parametrů, a měla by mít silnější reprezentační schopnosti, než identitu zkratky. Ve skutečnosti, zkratka-only gating a 1×1 konvoluce pokrývají řešení prostor zkratek identity (tj., mohly by být optimalizovány jako zkratky identity). Nicméně, jejich školení chyba je vyšší než totožnosti zástupce, což naznačuje, že degradace těchto modelů je způsobena optimalizační problémy, místo toho, reprezentační schopnosti.

použití aktivačních funkcí

experimenty ve výše uvedené části jsou za předpokladu, že aktivací po přidání je mapování identity. Ale ve výše uvedených experimentech je ReLU, jak je navrženo v prvním příspěvku. Dále zkoumáme dopad .

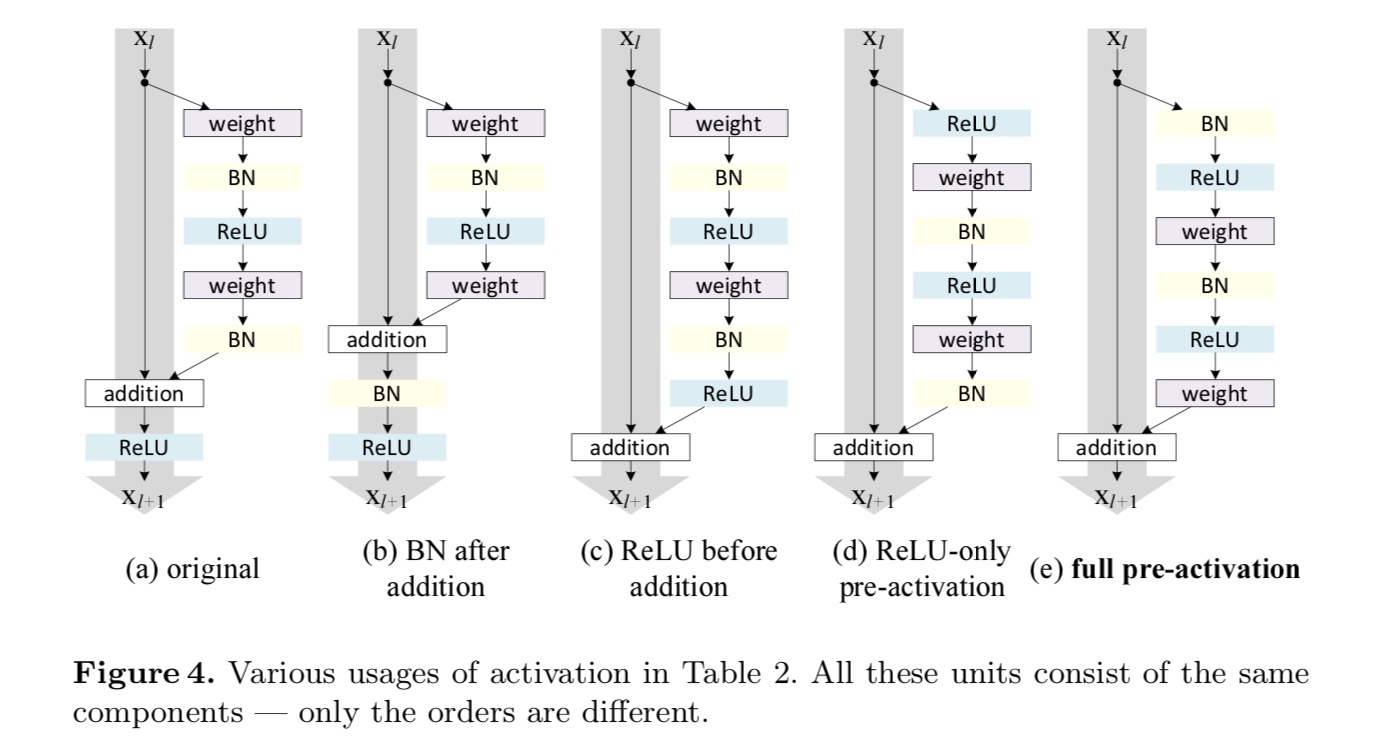
chceme provést mapování identity, které se provádí opětovným uspořádáním aktivačních funkcí (ReLU a / nebo BN, normalizace dávky). Na následujícím obrázku má původní zbytková jednotka v posledním papíru tvar na obr. 4(a – – BN se používá po každé hmotnostní vrstvě a ReLU se přijímá po BN s výjimkou toho, že poslední ReLU ve zbytkové jednotce je po elementárním přidání (=ReLU). Obr. 4 (b-e) ukázat alternativy, které jsme zkoumali.

Experimenty na Aktivaci

V této části jsme experimentovat s ResNet-110 a 164-vrstva Zúžení architektury (označován jako ResNet-164). Zbytková jednotka úzkého hrdla sestává z vrstvy 1×1 pro zmenšení rozměru, vrstvy 3×3 a vrstvy 1×1 pro obnovení rozměru. Jak bylo navrženo v posledním článku, jeho výpočetní složitost je podobná dvou-3×3 Zbytkové jednotce.

po aktivaci nebo předaktivaci?

v původním návrhu aktivace ovlivňuje obě cesty v další Zbytkové jednotce: . Dále vyvíjíme asymetrickou formu, kde aktivace ovlivňuje pouze cestu:, pro všechny . Přejmenováním notací máme následující podobu:

pro tuto novou zbytkovou jednotku stejně jako ve výše uvedené rovnici se nová aktivace po přidání stává mapováním identity. Tento návrh znamená, že pokud je nová aktivace po přidání asymetricky přijata, je ekvivalentní přepracování jako předběžná aktivace další Zbytkové jednotky. To je znázorněno na následujícím obrázku:

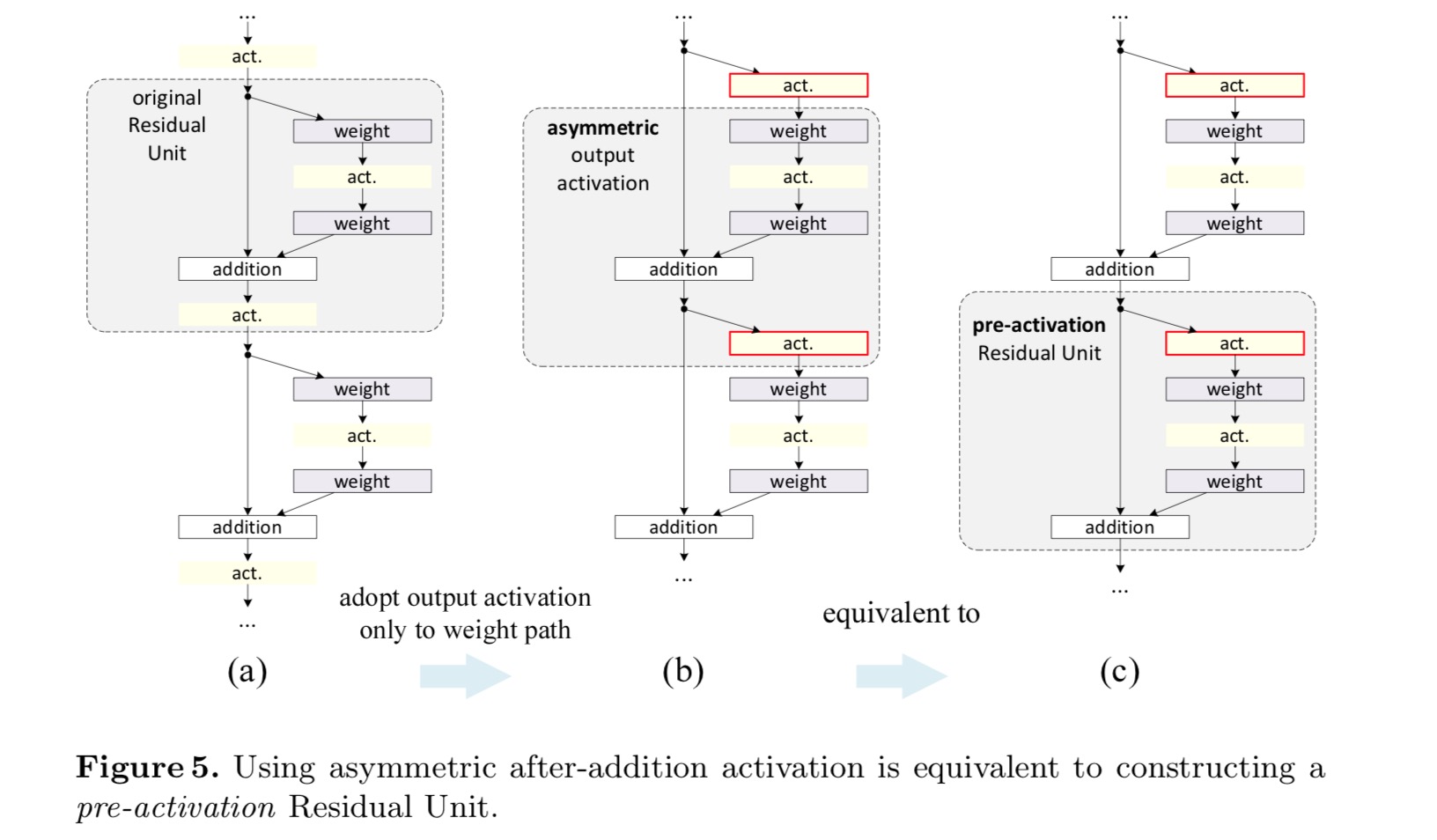
rozdíl mezi post-aktivace/pre-aktivace je způsobena přítomností element-wise toho. Pro prostou síť, která má n vrstev, existují n-1 Aktivace (BN / ReLU) a nezáleží na tom, zda je považujeme za post – nebo pre-aktivace. Ale pro rozvětvené vrstvy sloučené přidáním je důležitá pozice aktivace. Různá použití aktivace jsou zobrazena na obrázku 4.

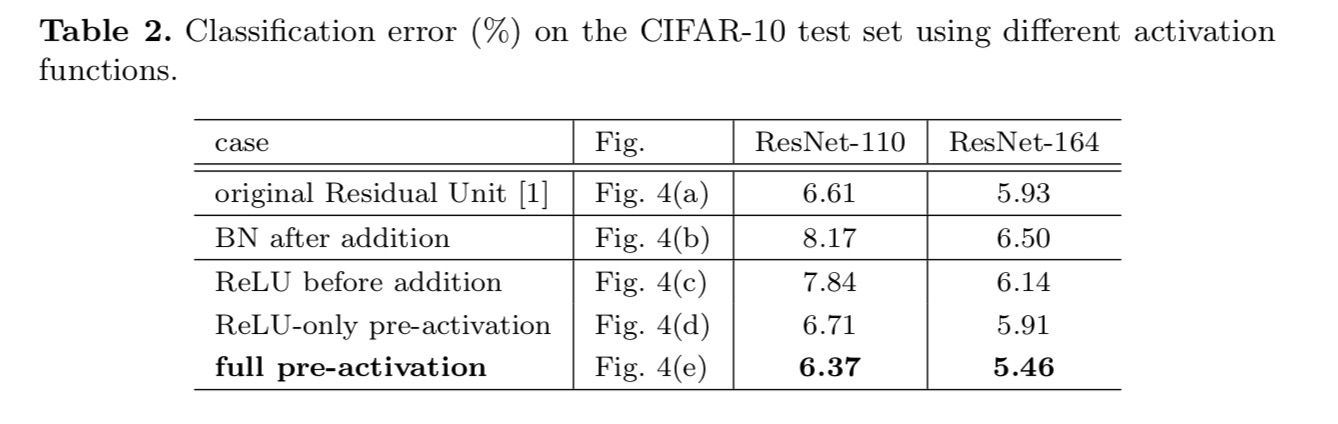
experimentujeme se dvěma takovými návrhy: (1) pouze předaktivace ReLU a (2) úplná předaktivace, kde jsou BN A ReLU přijaty před hmotnostními vrstvami. Nějak překvapivě, když BN a ReLU jsou oba používají jako pre-aktivace, výsledky jsou lepší zdravé marže

najdeme dopad pre-aktivace je dvojí. Nejprve je optimalizace dále usnadněna (ve srovnání se základním Resnetem), protože f je mapování identity. Za druhé, použití BN jako preaktivace zlepšuje regularizaci modelů.

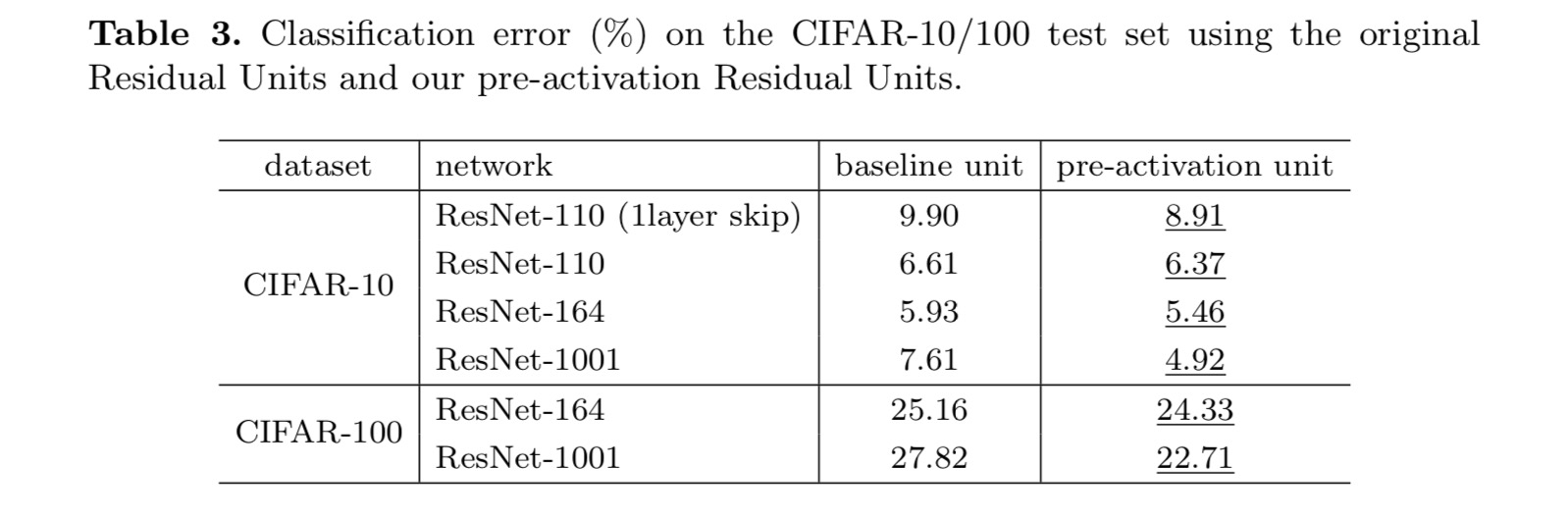
Závěr

Tento dokument zkoumá šíření formulace za připojení mechanismy hluboké zbytkové sítě. Naše derivace naznačují, že zkrácená spojení identity a aktivace identity po přidání jsou nezbytné pro plynulé šíření informací. Ablační experimenty demonstrují fenom-ena, které jsou v souladu s našimi derivacemi. Představujeme také 1000vrstvé hluboké sítě, které lze snadno vycvičit a dosáhnout lepší přesnosti.

Souhrnné Reziduální Transformace pro Hluboké Neuronové Sítě

Úvod

Výzkum na vizuální uznání prochází přechod od „funkce inženýrství“ na „inženýrské sítě“. Lidské úsilí bylo přesunuto k navrhování lepších síťových architektur pro reprezentace učení.

navrhování architektur se stává stále obtížnějším s rostoucím počtem hyperparametrů, zejména pokud existuje mnoho vrstev. Sítě VGG vykazují jednoduchou, ale účinnou strategii budování velmi hlubokých sítí: stohování stavebních bloků stejného tvaru. Tato strategie je zděděna Resnety, které ukládají moduly stejné topologie. Toto jednoduché pravidlo snižuje volné volby hyper parametrů a hloubka je vystavena jako základní dimenze v neuronových sítích. Navíc tvrdíme, že jednoduchost tohoto pravidla může snížit riziko nadměrné adaptace hyperparametrů na konkrétní datovou sadu. Robustnost VGG sítí a Resnetů byla prokázána různými úkoly vizuálního rozpoznávání a nevizuálními úkoly zahrnujícími řeč a jazyk.

Na rozdíl od VGG-sítí, rodina modelů Inception prokázala, že pečlivě navržené topologie jsou schopny dosáhnout přesvědčivé přesnosti s nízkou teoretickou složitostí. Počáteční modely se postupem času vyvíjely,ale důležitou společnou vlastností je strategie rozdělení-transformace-sloučení. V úvodní modul, vstup je rozdělena do několika nižší-dimenzionální vnoření (1×1 závitů), transformován sada speciálních filtrů (3×3, 5×5, atd.) a sloučeny zřetězením. Očekává se, že chování počátečních modulů rozdělené transformace a sloučení se přiblíží reprezentační síle velkých a hustých vrstev, ale s podstatně nižší výpočetní složitostí.

i přes dobrou přesnost byla realizace počátečních modelů doprovázena řadou komplikujících faktorů. I když pozor, kombinace těchto složek výnosu vynikající neuronové sítě recepty, to je obecně jasné, jak přizpůsobit Vzniku architektury do nové datové soubory/úkoly, zvláště když existuje mnoho faktorů, a hyper-parametry, které mají být navrženy.

V tomto příspěvku prezentujeme jednoduchou architekturu, která přijímá VGG/ResNets strategii z opakujících se vrstev, zatímco využití split-změnit-sloučit strategii v jednoduché, rozšiřitelný způsob. Modul v naší síti provádí sadu transformací, každý na low-dimenzionální vkládání, jejichž výstupy jsou sloučeny do shrnutí. Usilujeme o jednoduchou realizaci této myšlenky — transformace, které mají být agregovány, mají stejnou topologii. Tento návrh nám umožňuje rozšířit se na jakýkoli velký počet transformací bez specializovaných návrhů.

empiricky demonstrujeme, že naše agregované transformace překonávají původní modul ResNet, a to i za omezené podmínky zachování výpočetní složitosti a velikosti modelu. Zdůrazňujeme, že zatímco je poměrně snadné zvýšit přesnost zvýšením kapacity (bude hlubší a širší), metody, které zvyšují přesnost při zachování (nebo snížení) složitost jsou vzácné v literatuře.

naše metoda ukazuje, že kardinalita (Velikost souboru transformací) je konkrétní, měřitelná dimenze, která má kromě rozměrů šířky a hloubky zásadní význam. Experimenty prokazují, že rostoucí mohutnost je více efektivní způsob, jak získat přesnost než hlubší nebo širší, a to zejména, když hloubka a šířka začne dávat klesající výnosy pro stávající modely.

naše neuronové sítě, pojmenované ResNeXt (což naznačuje další dimenzi), překonávají ResNet-101/152, ResNet-200, Inception-v3 a Inception-ResNet-v2 na datovém souboru ImageNet classification. Zejména 101vrstvý ResNeXt je schopen dosáhnout lepší přesnosti než ResNet-200, ale má pouze 50% složitost. ResNeXt navíc vykazuje podstatně jednodušší návrhy než všechny počáteční modely.

metoda

přijmeme vysoce modularizovaný design podle VGG / Resnetů. Naše síť se skládá ze stohu zbytkových bloků. Tyto bloky mají stejnou topologii, a jsou předmětem dvou jednoduchých pravidel inspirován VGG/ResNets: (1) je-li produkovat prostorové mapy stejné velikosti, bloky sdílet stejnou hyper-parametry (šířka a filtr velikosti), a (2) pokaždé, když prostorové mapy se převzorkuje dolů o faktor 2, šířka bloků se násobí koeficientem 2. Druhé pravidlo zajišťuje, že výpočetní složitost, pokud jde o flopy (operace s plovoucí desetinnou čárkou, v #of multiply-adds), je zhruba stejná pro všechny bloky.

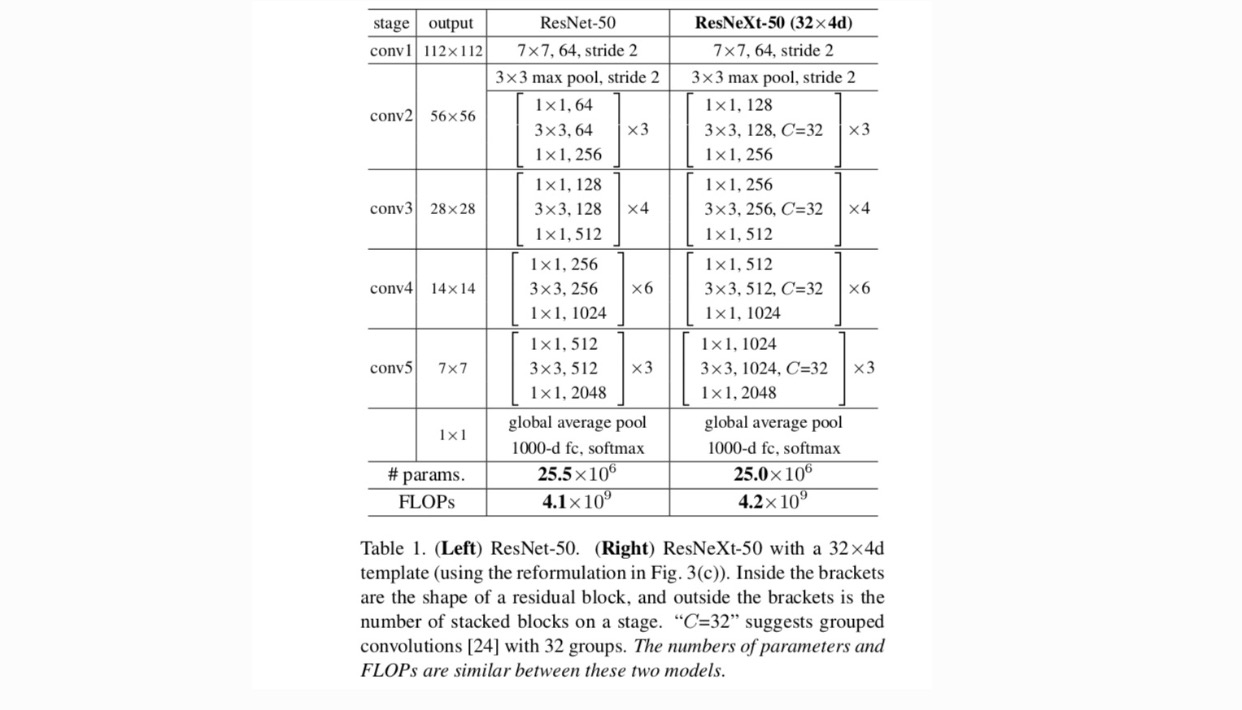
s těmito dvěma pravidly potřebujeme pouze navrhnout modul šablony a podle toho lze určit všechny moduly v síti. Takže tato dvě pravidla značně zužují designový prostor a umožňují nám soustředit se na několik klíčových faktorů. Sítě vytvořené těmito pravidly jsou uvedeny v tabulce 1.

nejjednodušší neuronů v umělé neuronové sítě provést skalární součin (vážený součet), což je elementární transformace provádí plně připojen a konvoluční vrstvy.

výše uvedená operace může být přepracována jako kombinace rozdělení, transformace a agregace. (1): Rozdělení: vektor je nakrájené jako low-dimenzionální vkládání, a ve výše, to je single-dimenze podprostoru (2) Transformace: low-dimenzionální reprezentace je transformován, a ve výše, to je prostě zmenšen: (3) Agregace: proměny ve všech embeddings jsou agregovány .

vzhledem k výše uvedené analýze jednoduchého neuronu uvažujeme o nahrazení elementární transformace (w_i, x_i) obecnější funkcí, která sama o sobě může být také sítí. Formálně prezentujeme agregované transformace jako:

kde může být libovolná funkce. Analogicky k jednoduchému neuronu by se měl promítnout do (volitelně nízkorozměrného) Vložení a poté jej transformovat.

označujeme jako kardinálnost. je v pozici podobné in, ale nemusí se rovnat a může to být libovolné číslo. Experimenty ukazují, že kardinalita je zásadní rozměr a může být účinnější než rozměry šířky a hloubky.

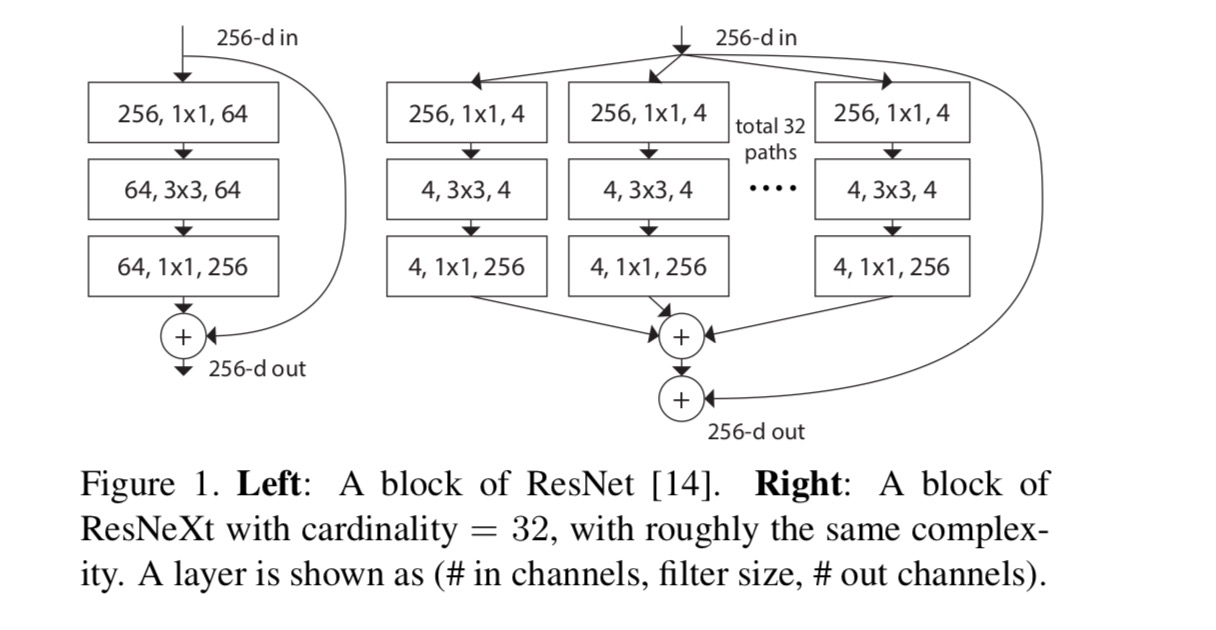
v tomto článku uvažujeme o jednoduchém způsobu návrhu transformačních funkcí: všechny mají stejnou topologii. Tím se rozšiřuje strategie ve stylu VGG opakujících se vrstev stejného tvaru. Individuální transformaci jsme nastavili na architekturu ve tvaru úzkého hrdla znázorněnou na obr. 1 (vpravo). V tomto případě první vrstva 1×1 v každé vytváří nízkorozměrné vkládání.

agregované transformace v poslední rovnice slouží jako zbytkové funkce:

kde je výstup.

vztahy mezi Resnext a Inception-ResNet / Grouped-Convolutions jsou znázorněny na následujícím obrázku:

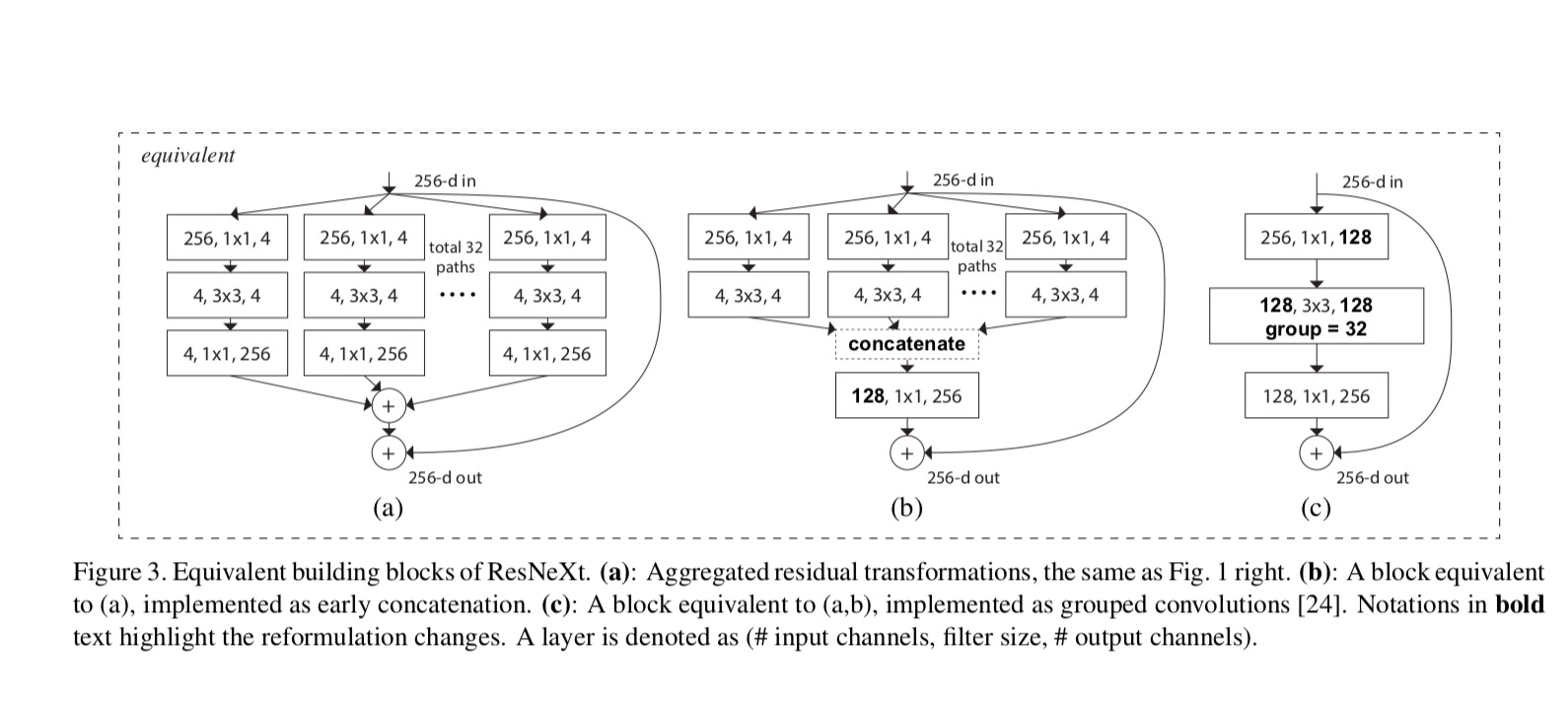
Když jsme se vyhodnotit různé cardinalities při zachování složitosti, chceme minimalizovat změny jiných hyper-parametry. 4-d na obr. 1 (vpravo)), protože může být izolován od vstupu a výstupu bloku. Tato strategie zavádí žádná změna jiných hyper-parametry (hloubka, nebo vstup/výstup šířka bloků), takže je užitečné pro nás se soustředit na dopad mohutnost.

Na obr. 1 (vlevo), původní resnet úzký blok má parametry a proporcionální propady (na stejné velikosti funkce mapy). S šířkou úzkého hrdla, naše šablona na obr. 1 (vpravo) má: parametry a proporcionální propady. Kdy a, toto číslo . Následující tabulka ukazuje vztah mezi kardinalitou a šířkou úzkého hrdla .

experimenty

Kardinalita vs. šířka. Musíme nejprve vyhodnotit, trade-off mezi mohutnost a zúžení šířky, podle dochovaných složitosti, jak jsou uvedeny v Tabulce 2. Tabulka 3 ukazuje výsledky. Ve srovnání s ResNet-50 má 32×4d ResNeXt-50 chybu ověření 22.2%, což je o 1.7% nižší než základní hodnota ResNet 23.9%. S rostoucí kardinálností z 1 na 32 při zachování složitosti se míra chyb stále snižuje. Kromě toho, 32×4d ResNeXt má také mnohem nižší, školení chyba než ResNet countetpart, což naznačuje, že zisky nejsou z regularizace ale ze silnější zastoupení.

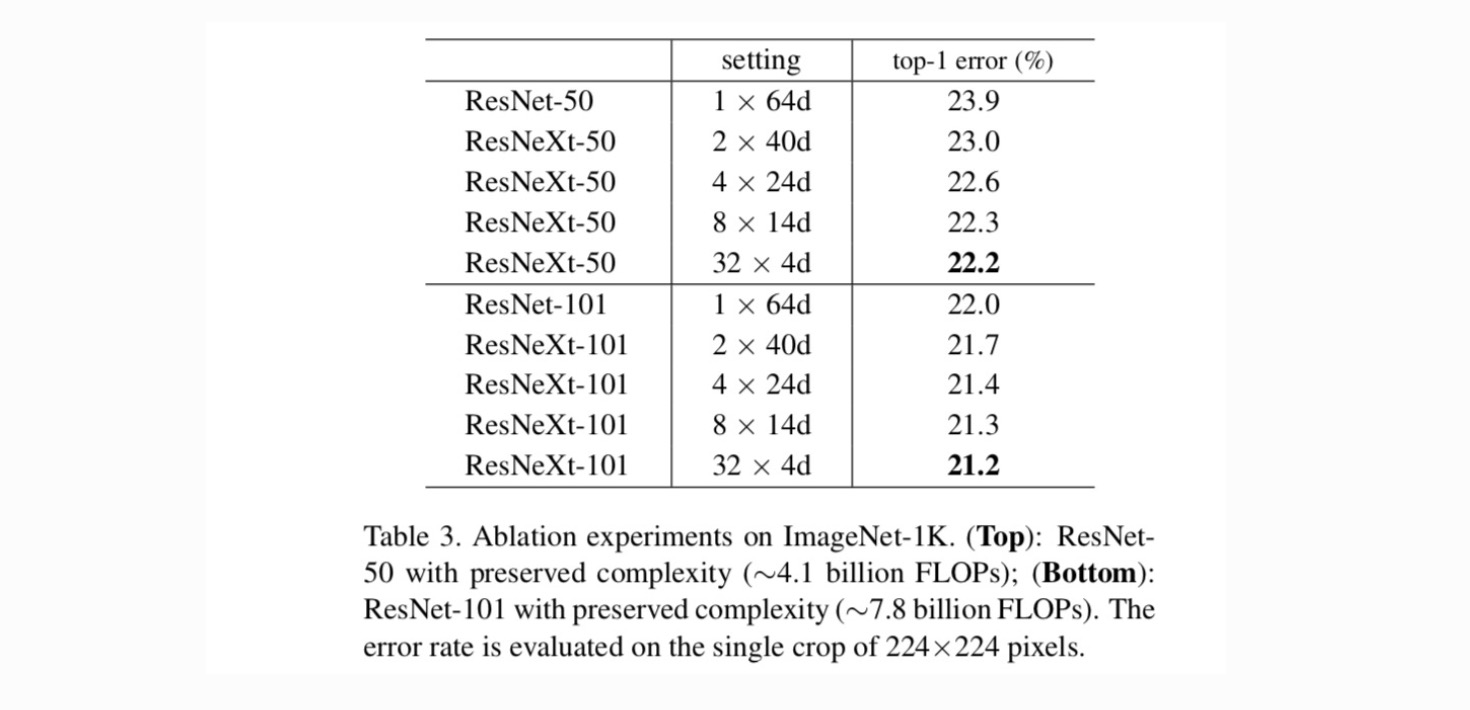
zvýšení Kardinality vs. hlubší/širší.

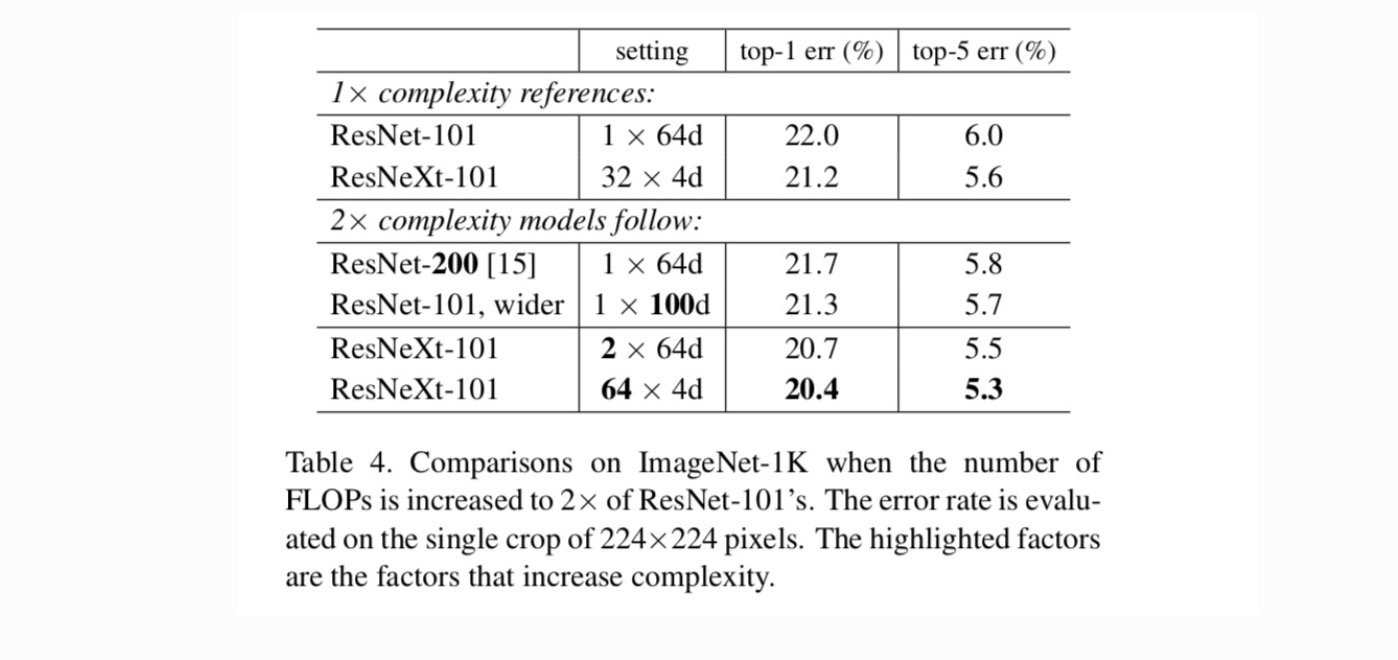
dále zkoumáme rostoucí složitost zvýšením kardinality C nebo zvýšením hloubky nebo šířky. Porovnáváme následující varianty (1), které jdou hlouběji do 200 vrstev. Přijmeme ResNet-200. (2) širší zvětšením šířky úzkého hrdla. (3) Rostoucí mohutnost zdvojnásobením C.

Tabulka 4 ukazuje, že rostoucí složitost o 2× důsledně snižuje chybová vs. ResNet-101 hodnot (22.0%). Ale zlepšení je malé, když jde hlouběji (ResNet-200, o 0,3%) nebo wider (širší ResNet-101, o 0,7%). Naopak rostoucí kardinalita C vykazuje mnohem lepší výsledky než jít hlouběji nebo širší.

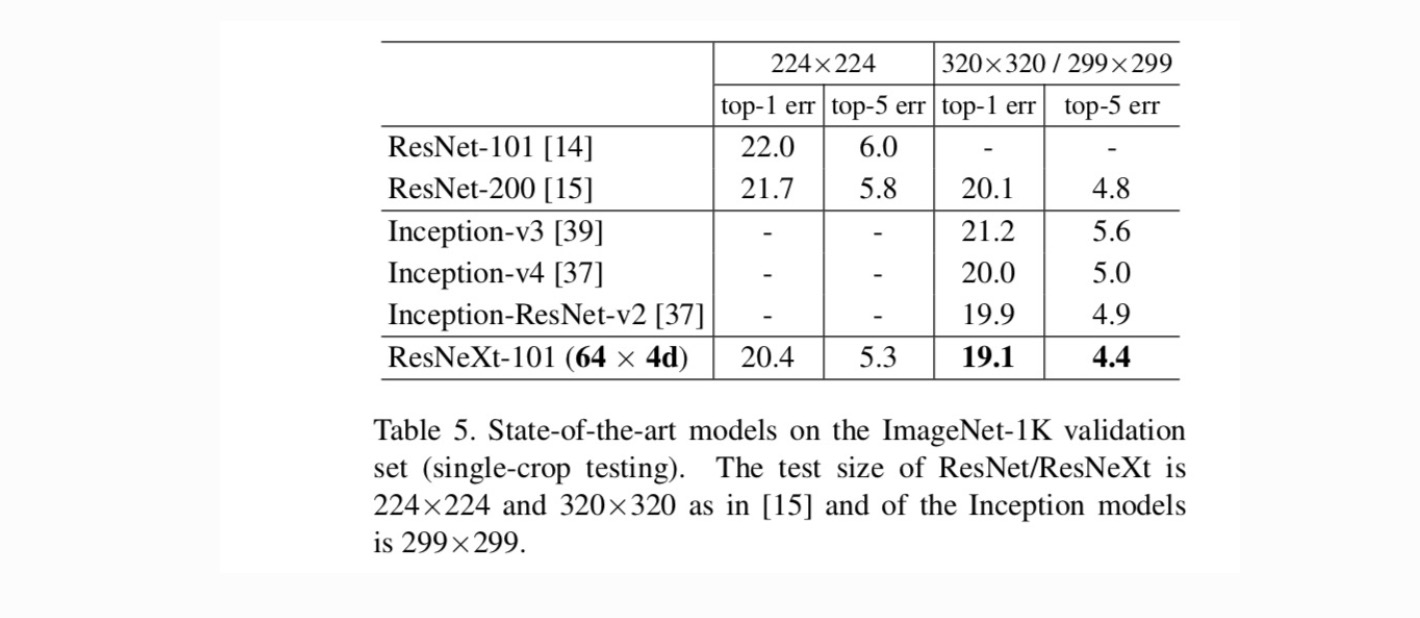
srovnání s nejmodernějšími výsledky. Tabulka 5 ukazuje více výsledků testování po jedné plodině na validační sadě ImageNet. Naše výsledky porovnat příznivě s ResNet, Vzniku-v3/v4, a Vzniku-ResNet-v2, dosažení jednotného-crop top-5 chybovosti 4,4%. Kromě toho je náš návrh architektury mnohem jednodušší než všechny počáteční modely a vyžaduje podstatně méně Hyper-parametrů, které je třeba nastavit ručně.