AMS:: Feature Column from the AMS

Publikováno v červnu 2008.
Geometrie planimetr
Guldin Věta
úplný výsledek
Planimeters a greenova Věta
Jiné druhy planimeters
zjistit více

Publikováno v červnu 2008.

druhý ze dvou sloupců o matematice zeměměřictví (první je zde). …

Bill Casselman
University of British Columbia, Vancouver, Kanada
cassi v matematice.ubc.ca

John Eggers
University of California, San Diego
jeggers na ucsd.edu

e-Mail známému

Vytisknout tento článek

planimetr je stolní přístroj pro měření ploch, obvykle v oblasti nepravidelné regiony na mapě nebo fotografie. Kdysi byly běžné, ale nyní byly z velké části nahrazeny digitálními nástroji.

následující obrázek poskytuje určitou představu o nastavení. Rameno tyče se volně otáčí kolem tyče, která je upevněna na stole. Sledovací rameno se otáčí kolem čepu, což je místo, kde se připojuje k polárnímu rameni. Můžete sledovat křivku ve směru hodinových ručiček s tracer, a jak si to měřicí kolo valí podél, a celková vzdálenost se valí se hromadí na číselníku. Podpěrné kolo zabraňuje převrácení věci. Na konci si přečtěte číslo z číselníku, a po násobení koeficientem v závislosti pouze na konkrétní konfiguraci planimetr, dostanete plochy uvnitř křivky.

následující obrázek vám poskytne lepší pohled na mechanismus.

nazýváme vozík sestavou kol, číselníkem a čepem. Na dalším obrázku se na to lépe podíváte a můžete vidět šnekový pohon, který způsobuje otáčení číselníku při pohybu měřicího kola.

Zde je schéma originální planimetr, z článku Jakob Amsler, který představil je:

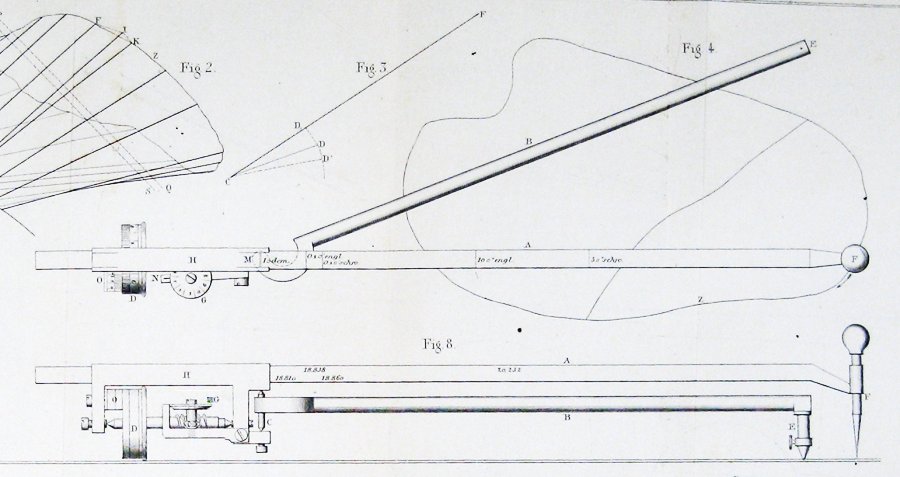
Jak může tak jednoduchá věc, opatření oblastech?

Geometrie planimetr

ve směru hodinových ručiček pohyb planimetr je směr opačný ke směru co se matematici rozhodli, by měl být pozitivní rotace. Spíše než porušovat tuto úmluvu, budeme od nynějška pracovat s matematickým planimetrem, ve kterém se pohybujete proti směru hodinových ručiček. Stejně jako fantazie jiných matematiků, na planetě nejsou žádné!

existují určitá omezení, jak umístit planimetr s ohledem na křivku, kterou chcete sledovat. Přeprava může být sklouzl podél tracer ruku, ale ve všech případech délky l sledovacího ramene je menší, než délka r pólu ruku. To znamená, že indikátor se nikdy nemůže dostat do vzdálenosti r – l od pólu. Na druhou stranu, když je plně rozšířena, tracer může nikdy dosáhnout za r + l. Takže křivka dohledat musí ležet v mezikruží mezi dva kruhy, jeden s poloměrem r – l, r + l.

Ve skutečnosti, to by mělo být jasné v okamžiku, že zbraně by nikdy neměla být zcela rozšířené, takže křivka dohledat musí ležet úplně uvnitř mezikruží. Dále je normálně pól umístěn na vnější straně křivky.

Pro daný bod v mezikruží jsou přesně dvě možné konfigurace planimetr, že umístěte tracer na místo. Výběr jednoho nebo druhého bodu znamená výběr znaménka pro druhou odmocninu. Říkáme tomu volba orientace pro planimetr. Je pozitivní, pokud je druhá odmocnina pozitivní. Jakmile je zvolena orientace, zůstane stejná, pokud není rameno zcela nataženo. Tohle se nesmí nikdy stát. Dokud je vaše křivka zcela v mezikruží, konfigurace planimetru se budou plynule a jedinečně měnit s cestou sledovače.

Další věc, kterou musíte udělat, je pochopit několik věcí o pohybu měřicího kola. Jak ukazuje následující obrázek, pokud se kolo pohybuje v přímce ve vzdálenosti C, kolo se otáčí úhlem θ = C / R, kde R je jeho poloměr.

takže je skutečně pravda, že rotace kola a vzdálenost ujetá sledovacím ramenem mají nějaký vztah k sobě navzájem. Ale tento vztah je trochu jemný. Pokud se rameno jen pohybuje rovně o vzdálenost C, oblast zametla bude lC, ale pokud se posune rovnoběžně k sobě, oblast zametla bude 0. V prvním případě se bod na obvodu kola bude pohybovat vzdáleností C. ve druhém případě se kolo vůbec nepohybuje. A pokud se rameno překládá šikmo, kolo se otočí o vzdálenost rovnající se nadmořské výšce rovnoběžníku pokrytého ramenem. Ve všech případech, kdy paže se promítá paralelně k sobě, oblasti smeten tím, že část tracer ruku mezi pivot a tracer se bude rovnat lC, kde C je vzdálenost měří podle otáčení kola. To je základní skutečnost týkající se pohybu ramene k pohybu měřicího kola.

způsob, jak to vyjádřit přesně to je, že bez ohledu na to, jak se ruka pohybuje, vzdálenost měřená kola je cesta integrál

, kde Γ je cesta, kterou urazí bod na rameno, kde měřicí kolo je připojen, n je jednotkový vektor kolmý na ruku v každém okamžiku, a t je jednotkový vektor směřující ve směru jízdy (tak, že, například, v případě, že rameno se pohybují paralelně k sobě skalární součin n a t je 0).

Guldin Věta

dále se budeme snažit, aby chování planimetr intuitivně jasné, ale nejprve budeme se podívat na zvláštní druh planimetr, a v tomto případě ukázat jako mnohem obecnější výsledek. Předpokládejme, že vezmeme jediné volně se pohybující rameno délky l a připojíme k němu měřicí kolo o poloměru R přímo ve středu.

pak pohybujeme ramenem kolem roviny. Pokud se měřící kolo otáčí celkovým úhlem θ radiánů, když se rameno pohybuje kolem, vzdálenost, kterou bod na obvodu urazí, je C = θR.

Guldinova věta. V této situaci je celková plocha vymetená ramenem produkt lC.

oblast je zde interpretována znaménkem. Pokud se rameno jen otáčí kolem svého středu, jedna polovina paže jde dopředu a druhá dozadu a obě se zruší.

již jsme viděli, že Guldinovo tvrzení je platné v případě, že ruka jen překládá. Samozřejmě se to ne vždy stane-rameno se může otáčet, jak se pohybuje, stejně jako překládat. Ale můžeme vidět, co se děje tím, že rozsekáme zametanou oblast následovně:

Protože měřicí kolo je ve středu ruce, protože ruka se otáčí, to squishes malé bloky, na jedné straně, jak to rozšiřuje je na ostatní. Tyto účinky se navzájem přesně vyruší.

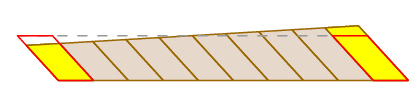
zcela rigorózní důkaz může být dán pomocí vzorce pro změnu proměnných v dvojí nedílnou a výraz pro cestovní kola jako dráhový integrál.

nyní předpokládejme, že kolo je umístěno někde jinde. Řekněme, že jeho poloha je c + V, kde c je střed paže a v vektor podél paže. Délka v zůstane pevná, řekněme na ρ. Cesta, kterou kolo sleduje, je c(t) + v (t). Dráhový integrál je nyní

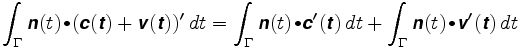
první integrál je vzdálenost volantem by cestovat, pokud to bylo ve středu paže. Ve druhém je vektor v(t) vždy kolmý na n a v (t) má konstantní délku. Vektor v (t) se pohybuje kolem kruhu o poloměru rovném ρ. Tečkový součin N A v'(t) je tedy jen podepsaná délka v'(t) a druhý integrál se rovná ρ krát celkové otáčení ramene. Proto:

Pokud se kolo je ve vzdálenosti ρ od středu paže, vzdálenost C volant opatření je C0 , vzdálenost, která by se měří, pokud kolo bylo ve středu, plus ρ krát celkový úhel θ, že rameno se otáčí.

můžete okamžitě vidět jeden jednoduchý případ tím, že otočíte rameno kolem jeho středu. V kombinaci s Guldinovou větou vidíme, že ve všech případech:

C = C0 + ρ θ
Oblast přehnala = l C0 = l C – l ρ θ

úplný výsledek

Guldin Vzorec dává podepsal oblasti – pokud budete otáčet zpět přes oblast, kolo jede pozpátku a zrušit oblasti jste již zahrnuty. Aplikujeme-li to na případ, kdy volné rameno se vrátí přesně tam, kde to začalo, vidíme, že lC je rovna ploše uzavřené oblasti vysledovat ven pravém konci ramene mínus, že v regionu zametl ze strany levé.

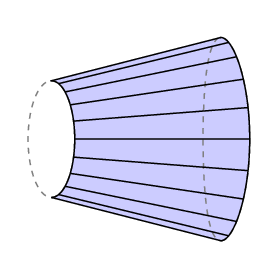
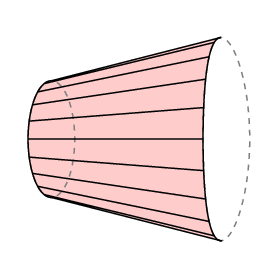
V případě polární planimetr, spodní paže je omezena na oblouku kružnice o poloměru r se středem v pólu, tedy l C je oblast vysledovat u tracer. Dále, normálně pól leží mimo oblast, která má být měřena, a v tomto případě musí být celkové množství otáčení ramene 0. Takže v tomto případě máme

Oblast regionu vysledovat = lC

Zde je obrázek součástí Jakob Amsler, vynálezce, v jeho původní papír na nástroj vynalezl:

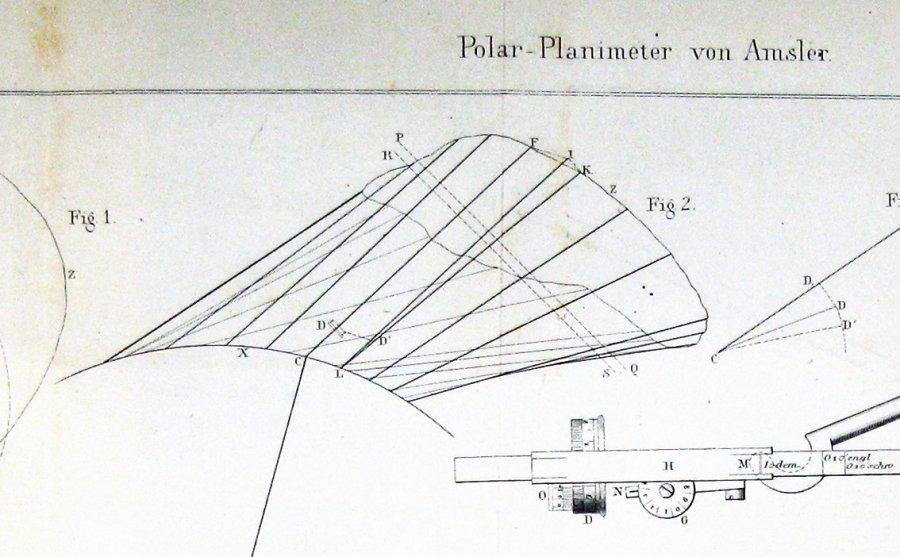
zdá se, docela jasné z toho, že Amsler odvozen jeho stavba přes nějakou formu Guldin věta.

Planimeters a greenova Věta

Jak jsme již zmínili, že zvolené orientaci planimetr, planimetr konfigurace je spojitá funkce sledovacího pozici. Řekněme, že zvolíme pozitivní orientaci. Pak můžeme připojit ke každému bodu z mezikruží jednotkový vektor n, jeden směřující proti směru hodinových ručiček a kolmo k tracer ruku na lokátor.

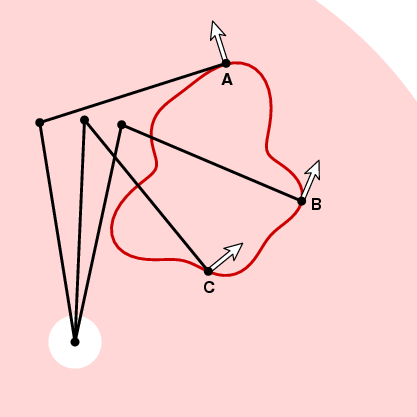
Jak měřicí kolo bude reagovat na pohyb podél křivky v příštím okamžiku závisí na úhlu mezi vektorem a jednotkové tečné vektorové křivky. Na obrázku výše se měřící kolečko nepohybuje, protože pohyb podél křivky je rovnoběžný se sledovacím ramenem. V B, pokud se indikátor pohybuje malou vzdáleností ds, tak bude měřicí kolo. A na C se měřící kolo bude pohybovat o určitou vzdálenost mezi 0 a ds. Abychom byli přesní, předpokládejme, že t je jednotkový tečný vektor v určitém bodě křivky. Pokud indikátor pohybuje vzdálenost ds podél křivky, v tomto bodě se měřící kolo posune vzdálenost D ds, kde d = n. t, skalární součin jednotkových vektorů t a n. Jinými slovy, pokud se pohybujeme po křivce Γ měřicí kolo se bude pohybovat celková vzdálenost se rovná integrál n . t ds (dot product), nebo

Ale protože každý bod z mezikruží odpovídá jedinečné pozitivní konfigurace planimetr, můžeme přiřadit vektor n pro každý vnitřní bod z mezikruží, a to proto definuje vektorové pole. Křivka Γ je hranicí jejího vnitřního Ω a podle jednoho z našich předpokladů je zcela obsažena v oblasti, kde je definováno n. Greenova věta nám říká, že integrál dráhy kolem hranice této oblasti je také roven určitému integrálu nad Ω: Proto

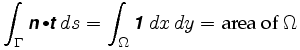
přesněji řečeno, greenova Věta nám řekli, že

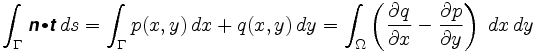
kde n = je vektorové pole podílí. Integrand v dvojitém integrálu se nazývá zvlnění vektorového pole.

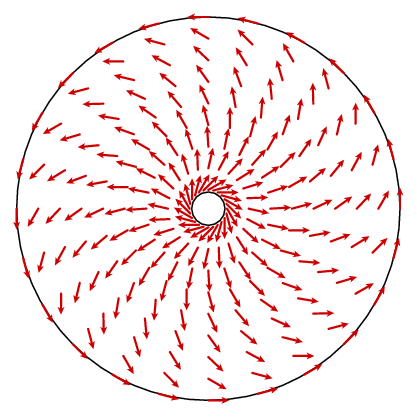
nezdá se, že si nás velmi daleko. Mělo by se stát, že zvlnění je konstanta 1. V zásadě bychom mohli najít vzorec pro vektorové pole n a vypočítat jeho zvlnění, ale to není příliš poučné. Můžeme však využít jiného faktu. Vektorové pole má kruhovou symetrii, což znamená, že je určeno tím, co je na jednom poloměru. Kosinusový zákon nám dává jednoduchý vzorec pro obvodovou složku.

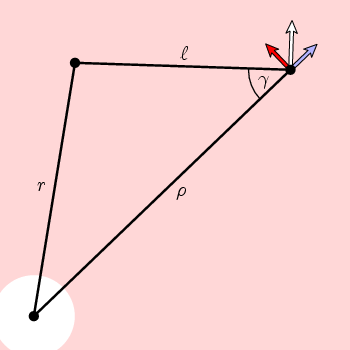
To vyplývá z jednoduché geometrie na tomto obrázku, že obvodová složka n je

f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)

skutečný bod Zelené Věta je, že za účelem ověření, že integrand je 1 stačí ověřit, že cesta nedílnou kolem vhodné malé cesty, je stejná jako oblast. Za tímto účelem si vybíráme naše regiony jako zde:

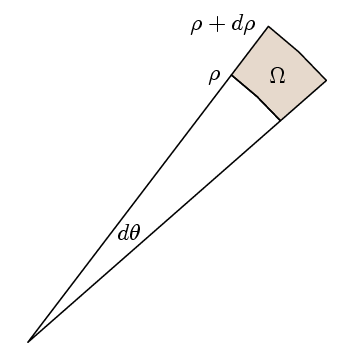
Pak se l krát dráhový integrál,

l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ

nebo

(θ/2) ( (ρ + dp) 2 – ρ 2)

což je oblast, v regionu Ω.

Jiné druhy planimeters

Guldin Věta znamená, že pohyb měřicí kolo vám řekne, oblasti vysledovat u tracer kdykoli rameno s měřicí kolo stopy křivku, ale má jeden konec omezuje na jednorozměrné křivky. To se děje, například s rolling planimetr, ve které je pivot je omezena na přímku tím, že na válcování válce.

zjistit více

stále dělá a prodává planimeters.
diferenciální a integrální počet Volume II, R. Courant, Blackie & Son, 1936. Část o Guldinově vzorci (s. 294-298) nabízí vysvětlení toho, jak planimetr funguje.
Amslerův původní článek, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Chybí schémata, ale jsou tady:
- Amsler první diagram
- Amsler druhý diagram
Naše díky Donna Sammis z Stony Brook University Knihovny pro vyhledání článku a její manžel Robert za poskytnutí fotografií z postav.

společnost, kterou Amsler založil, vyráběla nástroje až do 20. století. Tato fotografie ukazuje, logo, na sběrače verze planimetr:
„O Planimeters,“ EngineerSupply. Společnost také zveřejnila video na YouTube.