13.7: Franck-Condonin periaate

Franck-Condonin periaate kuvaa vibronitransitioiden intensiteettejä eli fotonin absorptiota tai emissiota. Sen mukaan kun molekyyli käy läpi elektronista siirtymää, kuten ionisaatiota, molekyylin ydinkonfiguraatio ei koe merkittävää muutosta. Tämä johtuu itse asiassa siitä, että ytimet ovat paljon massiivisempia kuin elektronit ja elektronisiirtymä tapahtuu nopeammin kuin ytimet pystyvät reagoimaan. Kun ydin asettuu uudelleen uuden elektronikonfiguraation kanssa, teorian mukaan sen on läpäistävä värähtely.

Jos kuvaamme pystysuuntaisen siirtymisen maasta jännitteiseen elektroniseen tilaan tapahtuvan värähtelyaaltofunktiosta,joka antaa todennäköisyysjakauman ytimien löytämiselle tietyllä avaruuden alueella, voimme määrittää tietyn värähtelytason todennäköisyyden päällekkäisintegraalista \(S_{v’, v}\), joka antaa värähtelyaaltofunktion päällekkäisyyden maassa ja jännittyneessä tilassa. \(V’\) kvanttiluvut tarkoittavat maatilaa ja \(v\) kvanttiluvut viritettyä tilaa. Transitiotodennäköisyys voidaan jakaa elektronisiin ja ydinosiin Kondonin approksimaation avulla.

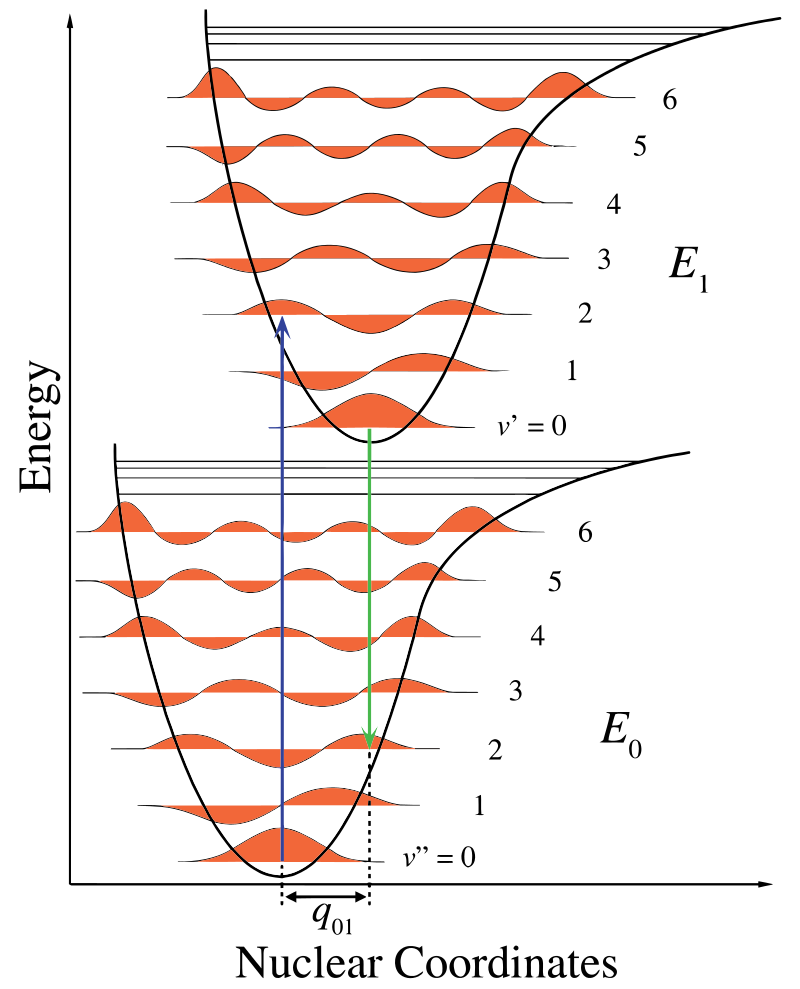
Kuvassa \(\PageIndex{1}\) ydinakseli näyttää internukleaarisen erkaantumisen seurauksen ja vibroninen Siirtymä osoitetaan sinisillä ja vihreillä pystynuolilla. Tämä luku osoittaa kolme asiaa:

1. absorptio johtaa korkeampaan energiatilaan,
2. fluoresenssi johtaa pienempään energiatilaan, ja
3. ydinkoordinaattien siirtyminen maanpinnan ja viritetyn tilan välillä on osoitus uudesta tasapainotilasta ydinten vuorovaikutuspotentiaalille. Se, että fluoresenssinuoli on lyhyempi kuin absorptio, osoittaa, että sillä on vähemmän energiaa tai että sen aallonpituus on pidempi.

Klassinen Condonin approksimaatio

Condonin approksimaatio on oletus, että elektronisiirtymä tapahtuu aikaskaalalla lyhyenä verrattuna ydinliikkeeseen niin, että siirtymätodennäköisyys voidaan laskea kiinteässä ydinasennossa.

tämä värähtelymuutos säilyy tilassa, jota kutsutaan nopeaksi elektroniseksi herätykseksi. Tuloksena olevat Coulombiset voimat tuottavat tasapainotilan, joka on esitetty käyränä pidettyjen ytimien kuviossa. Käännekohta voidaan kartoittaa piirtämällä pystyviiva alemman käyrän minimistä korkeamman elektronisen tilan leikkauspisteeseen. Tätä menetelmää kutsutaan pystysuuntaiseksi siirtymäksi, ja sitä on käsitelty aiemmin fotoelektronispektroskopian (toinen elektroninen spektroskopia) yhteydessä..

Franck-Condonin periaate selittää vibronisten siirtymien suhteelliset intensiteetit suhteuttamalla vibraatiomurroksen todennäköisyyden värähtelyaaltofunktioiden päällekkäisyyksiin. Sen mukaan vibraatiomurroksen esiintymistodennäköisyyttä painaa Franck-Condonin päällekkäisintegraali:

\

Franck-Condonin approksimaatiossa ytimiä pidetään ”kiinteinä” elektronisten siirtymien aikana. Näin ollen elektronisia siirtymiä voidaan pitää pystysuorina siirtyminä elektronisissa potentiaalienergiakäyrissä (vieeriset siirtymät Kuvassa \(\PageIndex{1}\)).

Quantum Franck-Condon-periaatteella

Franck-Condon-periaatteella on sekä klassinen että Kvanttisovellus. Klassisesti Franck-Condon-periaate on approksimaatio, jonka mukaan elektronisiirtymä tapahtuu todennäköisimmin ilman Muutoksia ytimien asemissa molekyylibiologiassa ja sen ympäristössä. Syntyvää valtiota kutsutaan Franck-Condonin valtioksi ja siihen liittyvää siirtymää vertikaaliseksi siirtymäksi. Tämän periaatteen kvanttimekaaninen muotoilu on, että vibronisen siirtymän voimakkuus on verrannollinen kahden siirtymiseen osallistuvan tilan värähtelyaaltofunktioiden päällekkäisen integraalin neliöön.

Franck-Condon-periaate perustuu Born-Oppenheimerin approksimaatioon, joka mahdollistaa elektronisten \(q\) ja ydinaaltofunktioiden erottamisen kokonaisaaltofunktiolle annettuna.

\

koska siirtymäoperaattori, \(\hat{\mu} (q)\), on riippuvainen vain elektronikomponentista, ydinkomponentit voidaan erottaa siirtymämomentin integraalista, joka määrää siirtymisen todennäköisyyden:

&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear limitys}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{El, I} \rangle \end{align}\]

jos ydinvoiman päällekkäisintegraali on nolla tälle siirtymälle, siirtymää ei havaita elektronikertoimen suuruudesta riippumatta.

\(S_{01}\) siirtyminen arvioituna harmonisen oskillaattorin mallissa

laskeaksesi zerothin maanpinnan tason (\(v=0\)) päällekkäisyyden ensimmäisen viritetyn tilan tason kanssa (\(v’=1\)) käytämme Hermiittistä polynomia \(H_1(x) =2x\) kuvataksemme viritettyä tilan aaltofunktiota (katso täältä katsaus harmoniseen oskillaattorin aaltofunktioon). Tässä \(x = \sqrt{\alpha} (R-Q_e)\).

\

, jossa nollapisteen aaltofunktio maanpinnan elektronisessa tilassa on

\

ensimmäinen viritetty tila-aaltofunktio viritetyssä sähköisessä tilassa on

\

zeroth Ground State-tason päällekkäisyys ensimmäisen viritetyn tilan tason kanssa (yhtälö \(\ref{fc01}\)) on tällöin

\

\

samat substituutiot voidaan tehdä kuin yllä siten, että integraali voidaan kirjoittaa kuten (ei esitetty ja osoitetaan kotitehtävissä) ja lopputuloksena

\

voitaisiin jatkaa ja laskea, että nollatason päällekkäisyys maan tilassa kaikilla korkeammilla valon värähtelytasoilla: \(s_{02}\), \(S_{03}\) jne. Jokainen termi vastaa siirtymää, jonka energia on erilainen, koska värähtelytasoilla on eri energiat. Absorptiokaistalla on tällöin etenemisen (Franck-Condon-etenemisen) ilmaantuminen eri tasojen välisistä siirtymistä kullakin omalla todennäköisyydellään.

Franck-Condonin progressiot

ymmärtääksemme yllä olevan kaavan merkityksen FC-tekijälle, tarkastelkaamme maanpäällistä ja viritettyä tilan potentiaalienergiapintaa arvolla \(T = 0\) Kelvin. Alla on esitetty kaksi tilaa erottaa 8000 cm-1 energia. Tämä on energiaerotus niiden potentiaalisten kaivojen pohjien välillä, mutta myös vastaavien nollapisteen energiatasojen välillä. Oletetaan, että värähtelytilan aaltoluku on 1000 cm-1 ja että sidoksen pituus kasvaa johtuen siitä, että elektroni poistetaan sidos-orbitaalilta ja asetetaan Anti-sidos-orbitaalille elektronisen herätyksen yhteydessä.

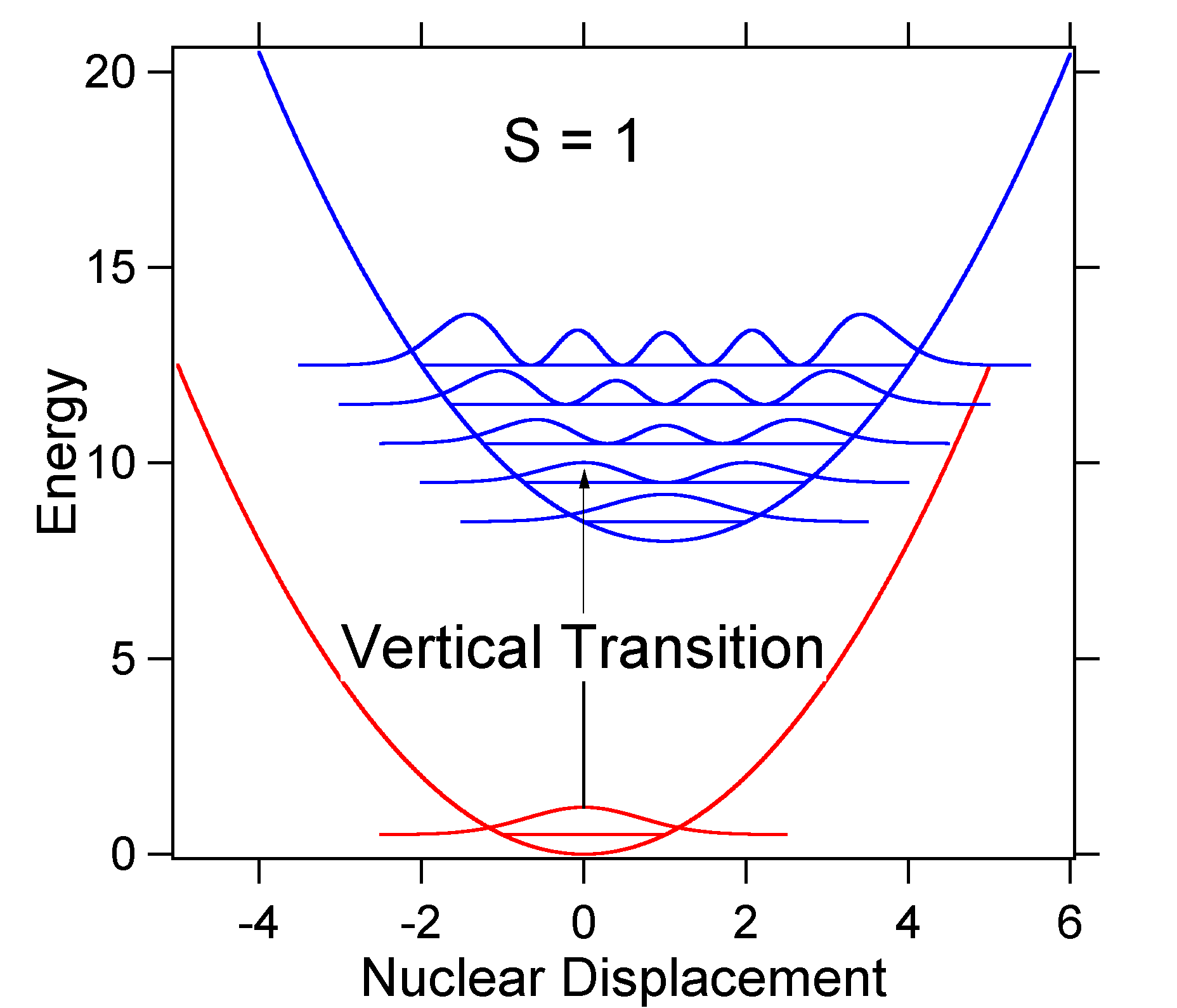
yllä olevan mallin mukaan Franck-Condon-tekijälle syntyisi ”stick” – spektri (Kuva \(\PageIndex{3}\)), jossa jokainen värähtelymuutos on äärettömän kapea ja siirtyminen voi tapahtua vain kun \(E = h\nu\) täsmälleen. Esimerkiksi potentiaalienergiapinnoille annettiin s = 1 ja siirtymätodennäköisyydeksi kullakin tasolla saadaan oheisessa kuvassa olevat tikut (Mustat).

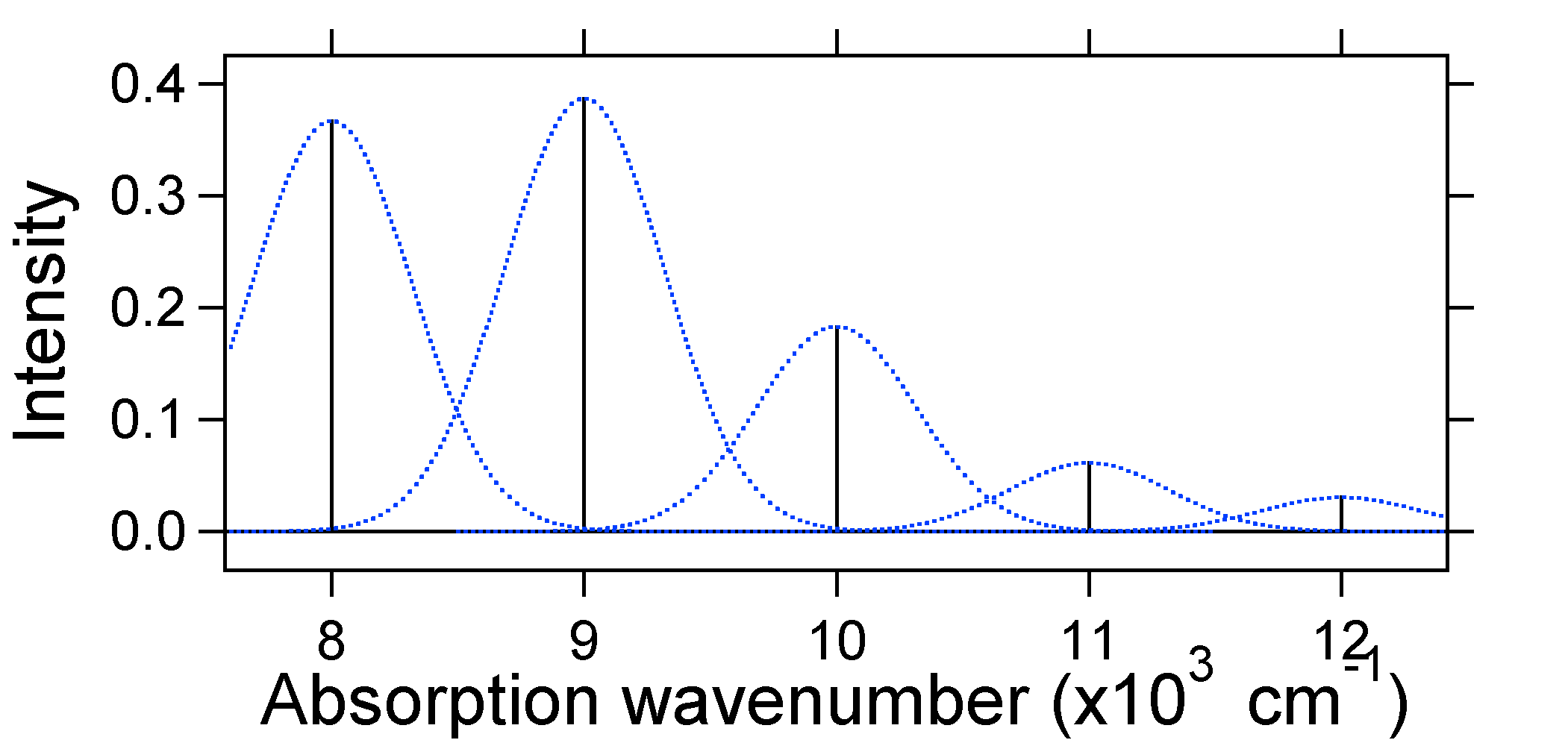
jokaista tikkua ympäröivät pistemäiset Gaussilaiset antavat realistisemman kuvan siitä, miltä absorptiospektrin tulisi näyttää. Tässä ensimmäisessä paikassa jokainen energiataso (keppi) saa jonkin verran leveyttä siitä, että valtion elinikä on rajallinen. Tällaista laajennusta kutsutaan homogeeniseksi laajennukseksi, koska se vaikuttaa samalla tavalla kaikkiin kokonaisuuden molekyyleihin. Myös kunkin molekyylin ympäristössä on pieniä eroja. Tällaista laajennusta kutsutaan epähomogeeniseksi laajennukseksi. Alkuperästä riippumatta yllä oleva malli luotiin Gaussin laajennuksella

maan ja viritetyn tilan välinen ydinsiirtymä määrittää absorptiospektrin muodon. Tarkastellaanpa sekä pienempää että suurta jännittynyttä tilasiirtymää. Jos \(S=½\) ja potentiaalienergiapinnat tässä tapauksessa ovat:

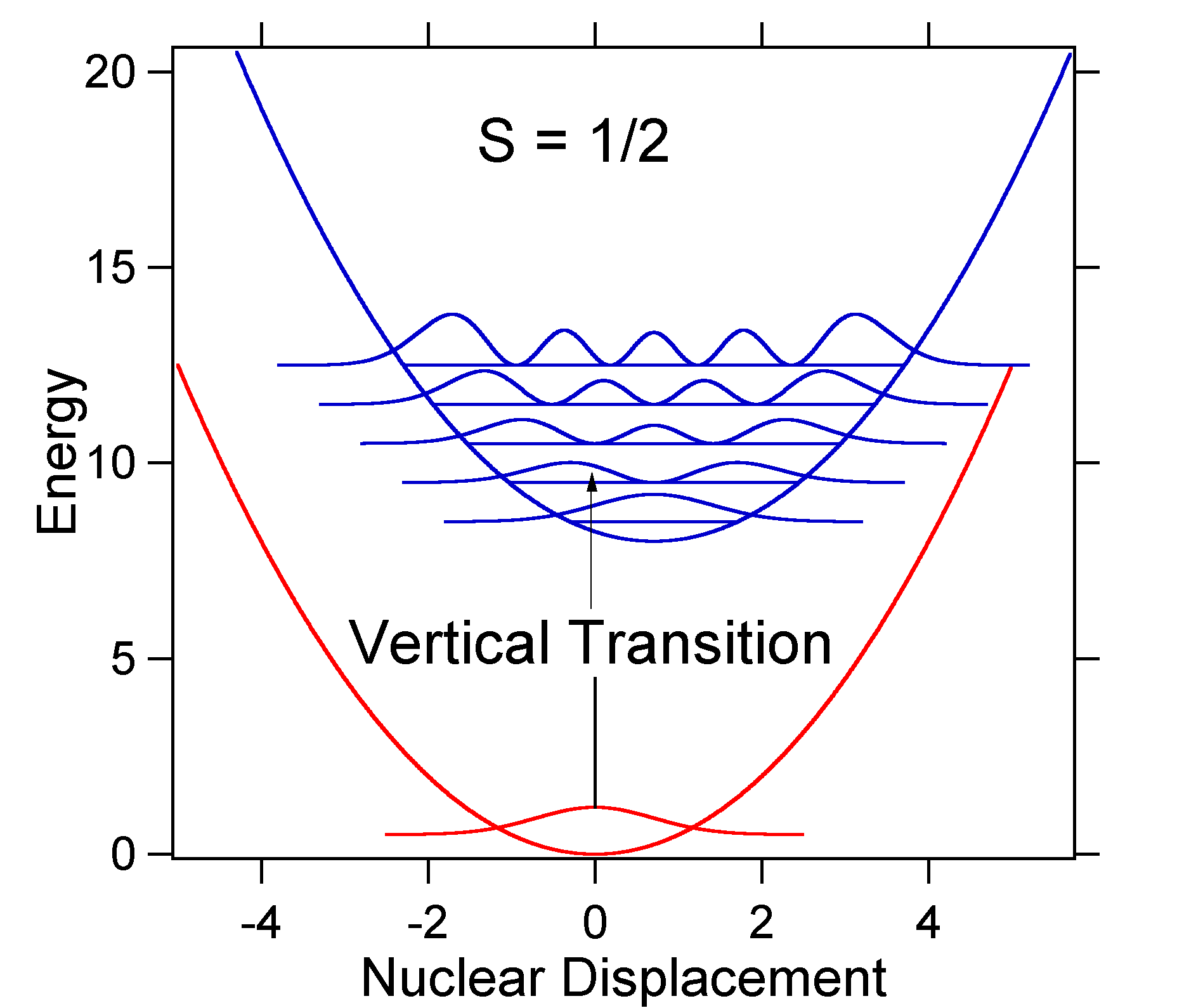
For this case the ”stick” spectrum has the appearance in Figure \(\PageIndex{5}\)

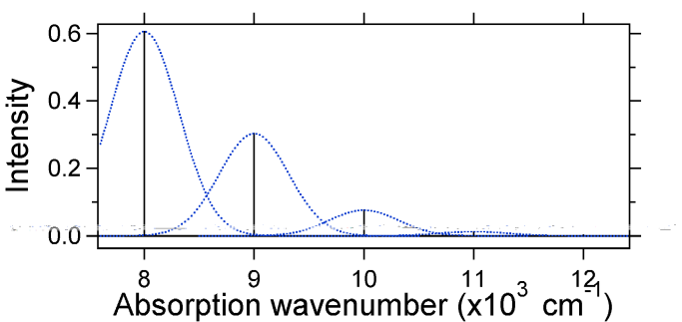
huomaa, että nolla-nolla tai \(s_{0,0}\) vibraatiosiirtymä on paljon suuri, jos siirtymä on pieni.

esimerkkinä suuremmasta siirtymästä on alla esitetty potentiaalienergiapintojen dispositio S = 2: lle.

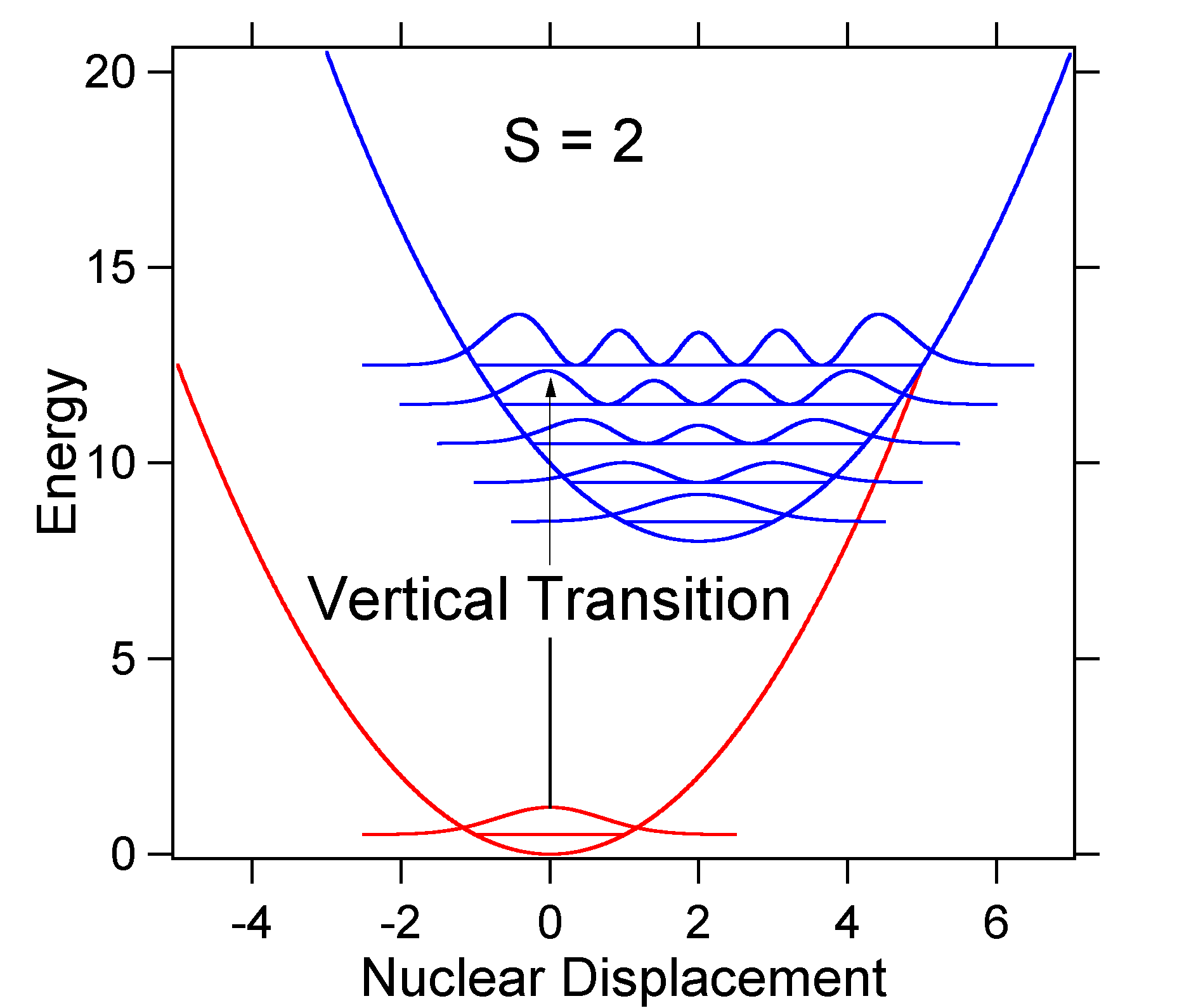
suurempi Siirtymä johtaa maanpinnan tason pienempään päällekkäisyyteen viritetyn tilan V = 0 tason kanssa. Maksimiteho saavutetaan suuremmilla värähtelytasoilla, kuten Stickin spektrissä on esitetty.

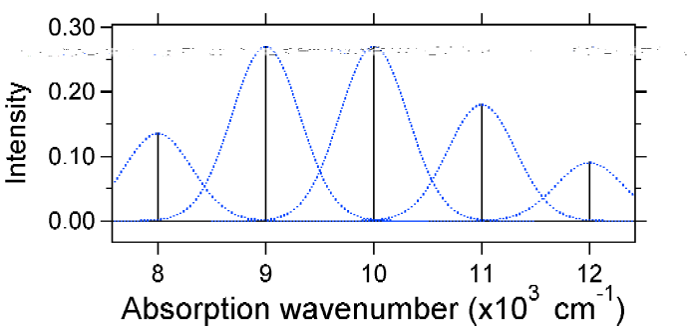
alla piirretyillä absorptiospektreillä on kaikilla sama integroitu intensiteetti, mutta niiden muodot muuttuvat, koska viritetyn tilan potentiaalienergiapinnan Siirtymä vaihtelee.

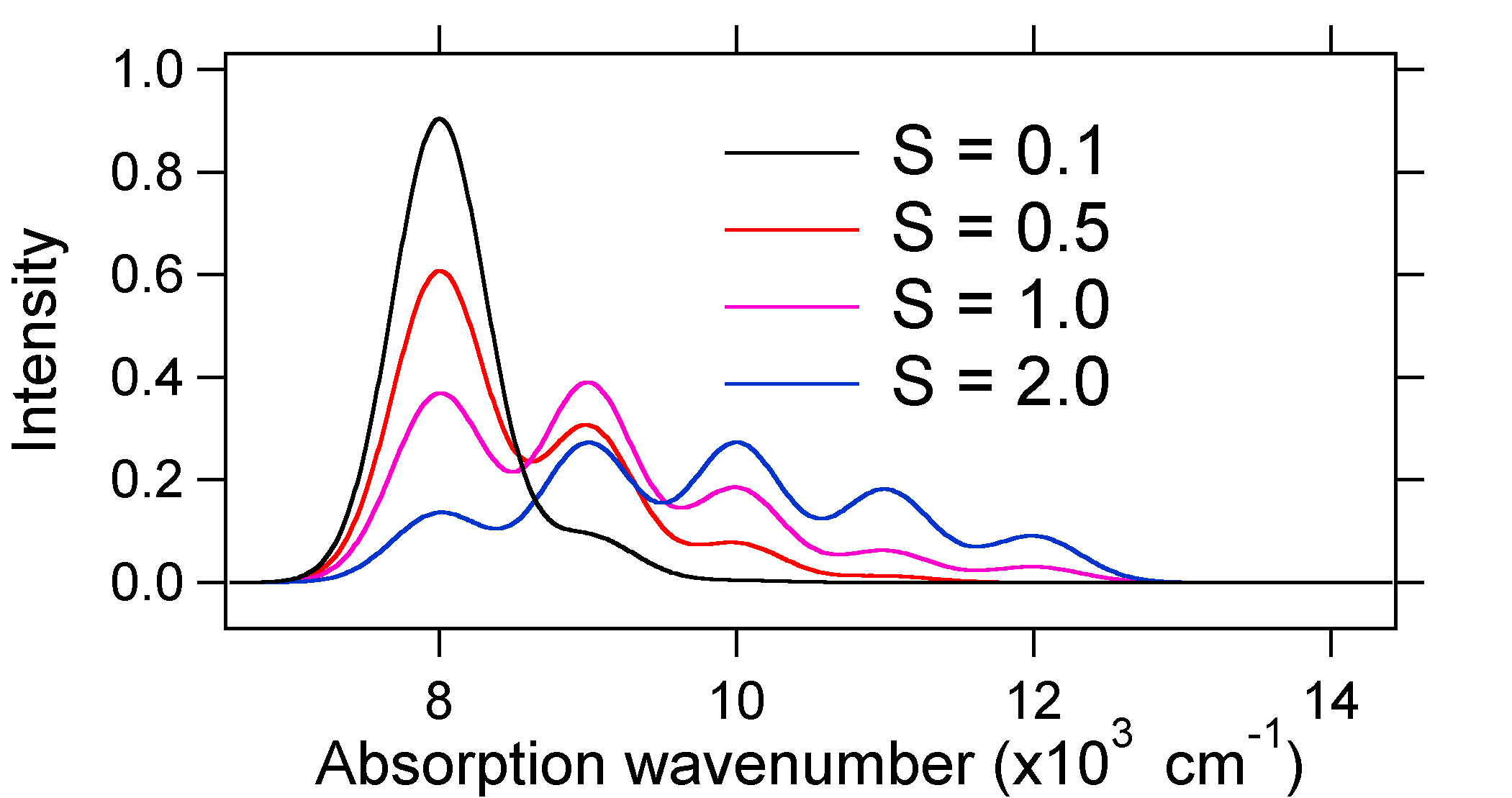
joten relatiivisten vibronikaistojen intensiteettien luonne voi kertoa, onko tasapainoisessa ydinkoordinaatistossa siirtymää, joka liittyy siirtymävaiheeseen. Milloin joukkolainan pituus kasvaa(eli \(Q_e > R_e\))? Tämä tapahtuu, kun elektroni edistyy sitoutumattomalta molekyyliorbitaalilta sitoutumattomalle tai sitoutumattomalle molekyyliorbitaalille (eli kun sidosjärjestys on vähemmän viritetyssä tilassa kuin maatilassa).

• sitoutumattomat molekyyliorbitaalit \(\rightarrow\) sitoutumattomat molekyyliorbitaalit
• sitoutumattomat Molekyyliorbitaalit \(\rightarrow\) sitoutumattomat molekyyliorbitaalit
• Sitoutumattomat Molekyyliorbitaalit \(\rightarrow\) sitoutumattomat molekyyliorbitaalit

lyhyesti, kun sidosjärjestys on jännittyneessä tilassa pienempi kuin maatilassa, niin \(Q_e > r_e\); bondlength kasvaa, kun tämä tapahtuu.

avustajat

Matthew Zi Ziering

Stefan Franzen (Pohjois-Carolinan osavaltionyliopisto)