
keinotekoinen neuroverkko (Ann) muodostuu monista toisiinsa liittyneistä neuroneista:
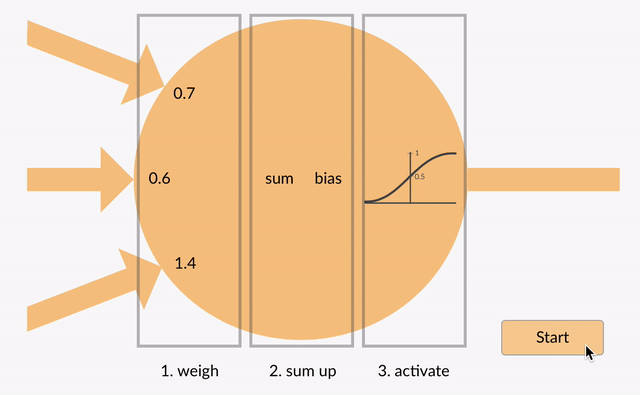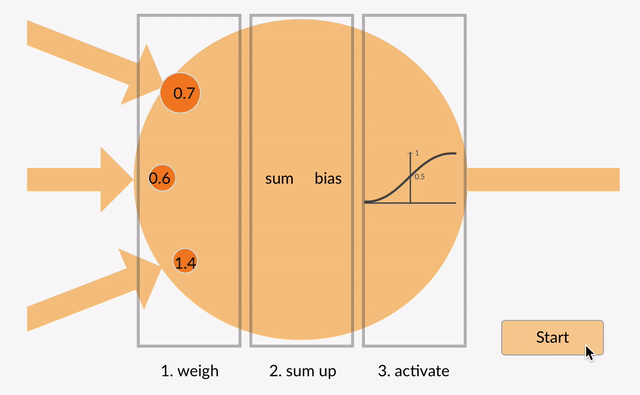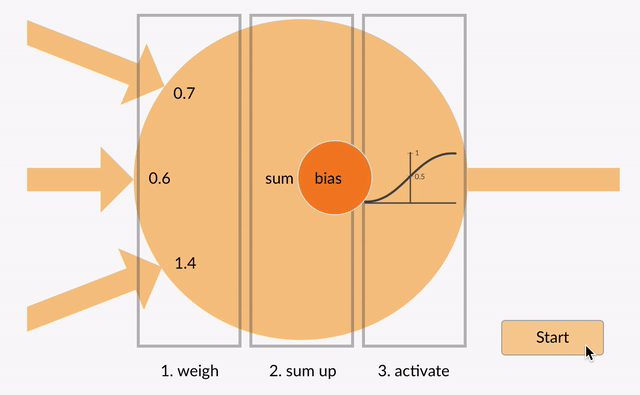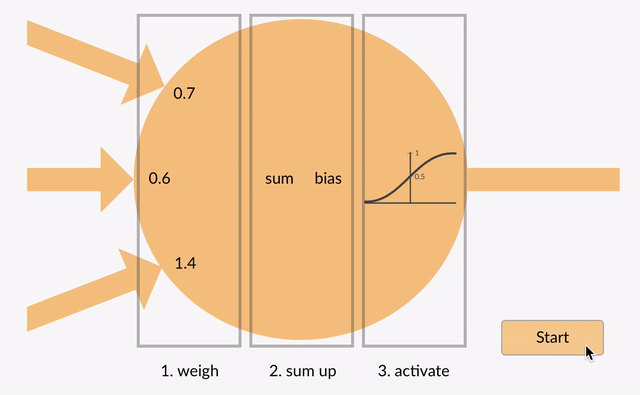
jokainen hermosolu ottaa joitakin liukulukuja (esim.1, 0, 0, 5, -1.0) ja kertoo ne joillakin muilla liukulukuluvuilla (esim. 0.7, 0.6, 1.4), joita kutsutaan painoiksi (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Painot toimivat mekanismina, jolla voidaan keskittyä tiettyihin syötteisiin tai jättää ne huomiotta.

painotetut tulot sitten summataan yhteen (esim. 0.7 + 0.3 + -1.4 = -0.4) yhdessä bias-arvon kanssa (esim.-0.4 + -0.1 = -0.5).
summattu arvo (x) muuttuu nyt lähtöarvoksi (y) neuronin aktivointifunktion (y = f(x)) mukaan. Alla on esitetty muutamia suosittuja aktivointifunktioita:

esim.-0.5 → -0.05 jos käytämme vuotavaa korjattua lineaarista yksikköä (leaky Relu) aktivointifunktio: y = f(x) = F(-0.5) = max(0.1*-0.5, -0.5) = Max(-0.05, -0.5) = -0.05
neuronin ulostuloarvo (esimerkiksi -0,05) on usein toisen hermosolun tulo.
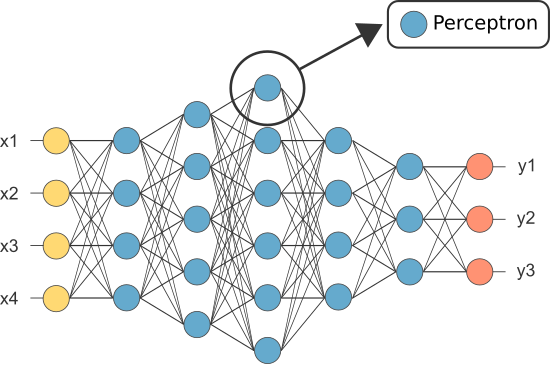
kuitenkin yksi ensimmäisistä ans tunnettiin nimellä Perceptron ja se koostui vain yksi neuroni.

perceptronin (vain) neuronin ulostulo toimii lopullisena ennusteena.

antaa koodata omaa perceptronia:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Huom.Emme ole sisällyttäneet mitään oppimisalgoritmia yllä olevaan esimerkkiimme — käsittelemme oppimisalgoritmeja toisessa tutoriaalissa)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()


joten miksi tarvitsemme annissa niin monta neuronia, jos yksikin riittää (luokittelijana)?

valitettavasti yksittäiset neuronit pystyvät luokittelemaan vain lineaarisesti eroteltavaa dataa.

kuitenkin yhdistämällä neuronit yhteen yhdistämme oleellisesti niiden päätösrajat. Siksi monista neuroneista koostuva ANN pystyy oppimaan monimutkaisia, epälineaarisia päätöksenteon rajoja.

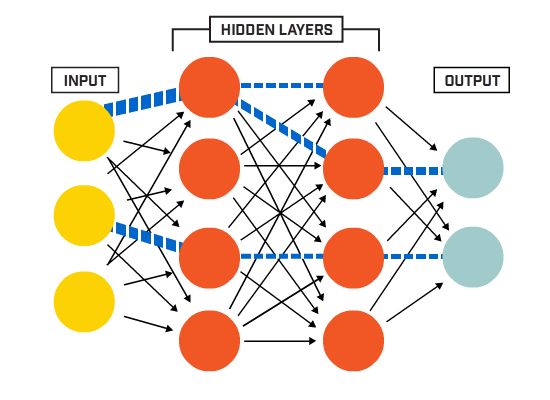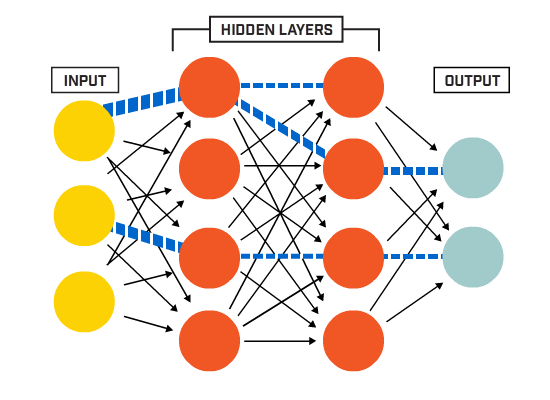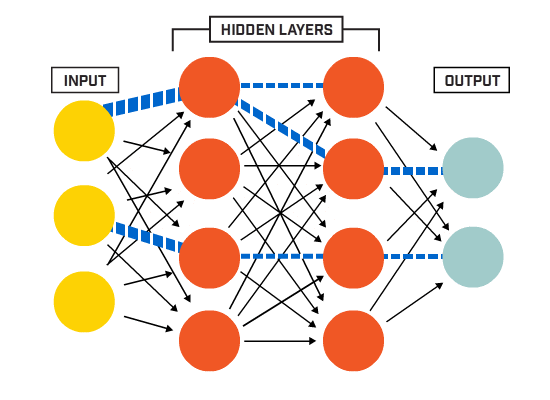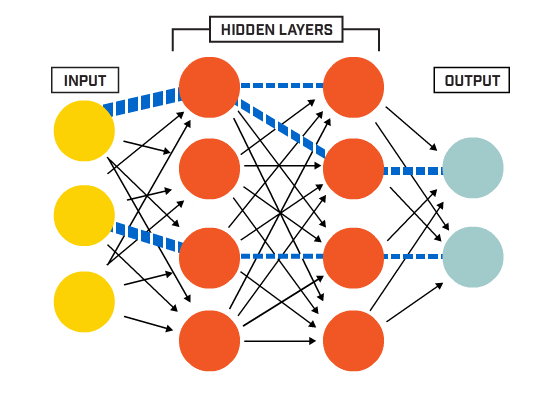
neuronit ovat yhteydessä toisiinsa tietyn verkkoarkkitehtuurin mukaisesti. Vaikka arkkitehtuureja on erilaisia, lähes kaikki niistä sisältävät kerroksia. (HUOM.: Saman kerroksen neuronit eivät yhdisty toisiinsa)
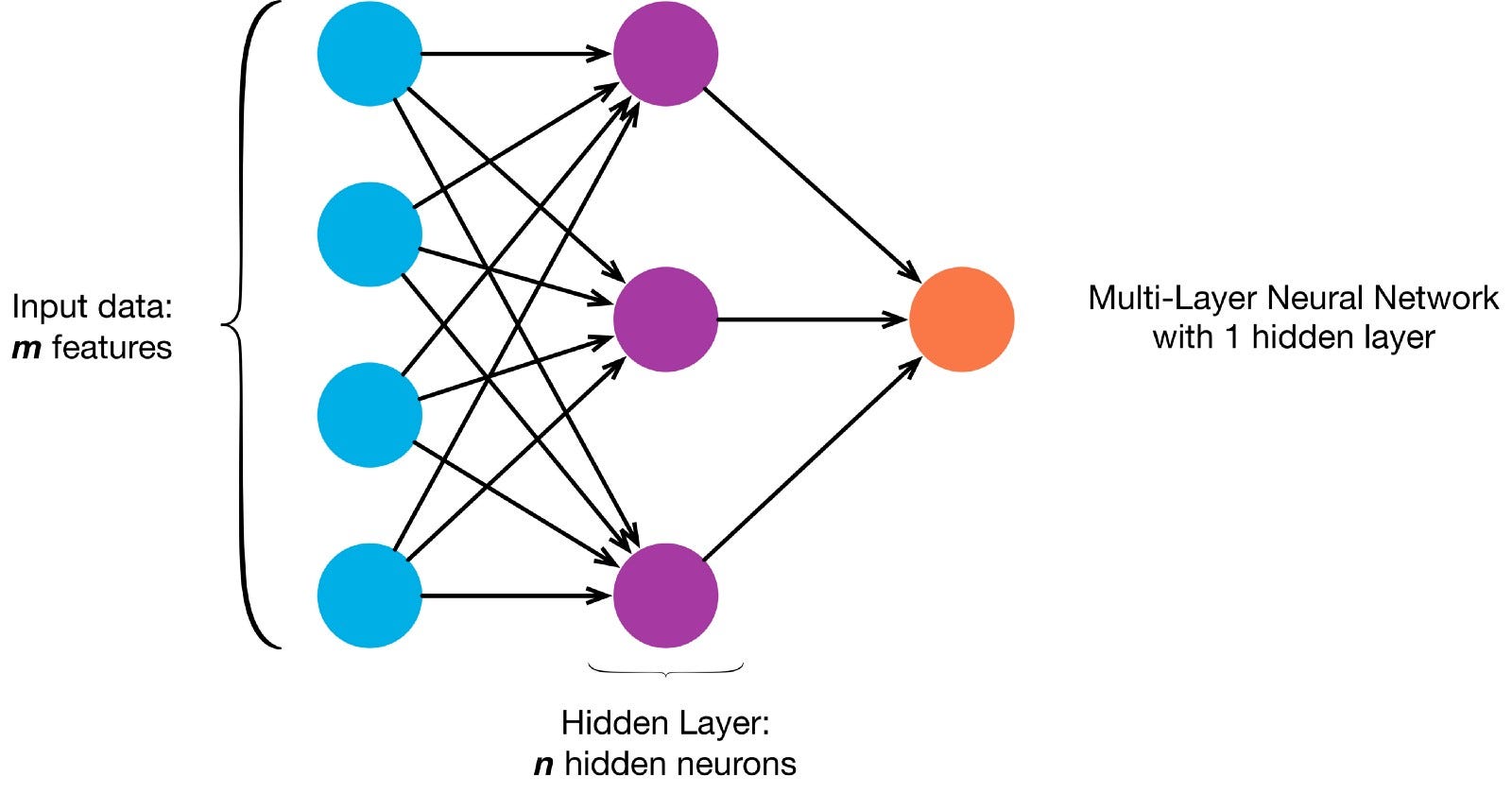
on tyypillisesti tulokerros (sisältää useita neuroneja yhtä suuri kuin tietojen syöttöominaisuuksien määrä), lähtökerros (joka sisältää neuronien määrän yhtä monta luokkaa) ja piilotettu kerros (joka sisältää minkä tahansa määrän neuroneja).

voi olla useampia piilokerroksia, joiden avulla neuroverkko oppii monimutkaisempia päätöksentekorajoja (mikä tahansa neuraalinen verkkoa, jossa on useampi kuin yksi piilokerros, pidetään syvänä neuroverkkona).
Lets build a deep NN to paint this picture:

lets download kuva ja sen pikselien lataaminen taulukkoon
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
nyt Annin opettaminen maalaamaan on valvottu oppimistehtävä, joten meidän on luotava merkityt koulutussarjat (koulutustietoissamme on Tulo-ja odotusetiketit jokaiselle syötölle). Harjoitustuloilla on 2 arvoa (kunkin pikselin x -, y-koordinaatit).
kuvan yksinkertaisuuden vuoksi tätä ongelmaa voisi oikeastaan lähestyä jommallakummalla kahdella tavalla. Luokitteluongelma (jossa neuroverkko ennustaa kuuluuko pikseli ”siniseen” vai ”harmaaseen” luokkaan XY-koordinaattiensa perusteella) tai regressio-ongelma (jossa neuroverkko ennustaa pikselin RGB-arvot sen koordinaattien perusteella).
Jos tätä käsitellään regressio-ongelmana: harjoitustuloksilla on 3 arvoa (normalisoidut R -, g-ja b-arvot kullekin pikselille). – Käytetään tätä menetelmää toistaiseksi.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
nyt lets create our ANN:

- siinä pitäisi olla 2 hermosolua tulokerroksessa (koska on olemassa 2 arvoa otettavaksi: x&Y-koordinaatit).
- siinä pitäisi olla 3 hermosolua lähtökerroksessa (koska opittavia arvoja on 3: R, g, b).
- piilotettujen kerrosten lukumäärä ja neuronien lukumäärä kussakin piilotetussa kerroksessa on kaksi hyperparametriä kokeiltavaksi (sekä niiden aikakausien lukumäärä, joita varten sitä koulutamme, aktivointifunktio jne.) — käytän 10 piilotettua kerrosta,joissa on 100 neuronia kussakin piilotetussa kerroksessa (tehden tästä syvän neuroverkkoa)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
koulutettu verkko voi nyt ennustaa normalisoidut rgb-arvot mille tahansa koordinaatille (esim. x, y = 1,1).
ann.predict(])
array(])
antaa Annin avulla ennustaa rgb — arvot jokaiselle koordinaatistolle ja näyttää ennustetut rgb-arvot koko kuvalle nähdäkseen, miten hyvin se pärjäsi (laadullisesti-jätämme arviointimittarit toiselle tutoriaalille)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

yritä vaihtaa hyperparametrit saadaksesi parempia tuloksia.
Jos tätä ei käsitellä regressio-ongelmana vaan luokitteluongelmana, harjoitustuloksilla on 2 arvoa (pikselin todennäköisyydet kuuluvat kumpaankin luokkaan: ”sininen” ja ”harmaa”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
voimme rakentaa annimme binääriluokittajaksi, jossa on 2 neuronia tulokerroksessa, 2 neuronia lähtökerroksessa ja 100 neuronia piilokerroksessa (10 piilotettua kerrosta)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
koulutetun annin avulla voidaan nyt ennustaa, mihin luokkaan kukin pikseli kuuluu (0: ”harmaa” tai 1: ”Sininen”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: ”grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

