Deep Residual Networks

Deep residual networks (ResNet) vei Deep Learningin myrskyn, kun Microsoft Research julkaisi Deep Residual Learningin kuvantunnistusta varten. Nämä verkostot johtivat 1. sijalle kaikissa ImageNet-ja COCO 2015-kilpailujen viidessä pääradassa, jotka käsittelivät kuvanluokitusta, objektien tunnistusta ja semanttista segmentointia. Resnetien kestävyys on sittemmin todistettu erilaisilla visuaalisella tunnistustehtävillä sekä ei-visuaalisilla tehtävillä, joihin liittyy puhe ja kieli. Käytin Resnetiä myös muiden syväoppimismallien ohella Väitöskirjatutkimuksessani.

tässä viestissä tiivistetään alla olevat kolme artikkelia, jotka ovat kaikki Resnetin keksijän Kaiming Hein kirjoittamia tai yhdessä kirjoittamia, koska uskon, että alkuperäiset paperit antavat mallin / verkkojen intuitiivisimman ja yksityiskohtaisimman selityksen. Toivottavasti, tämä viesti voisi auttaa sinua saamaan paremman käsityksen ydin jäljellä verkkojen.

• syvän Jäännösoppimisen kuvantunnistukseen
• identiteetin kartoitukset syvissä Jäännösverkoissa
• yhdistetyt Jäännösmuunnokset syvissä Neuroverkoissa

intuitio syvässä Jäännösverkossa (stackoverflow ref)

jäännöslohko näkyy seuraavasti:

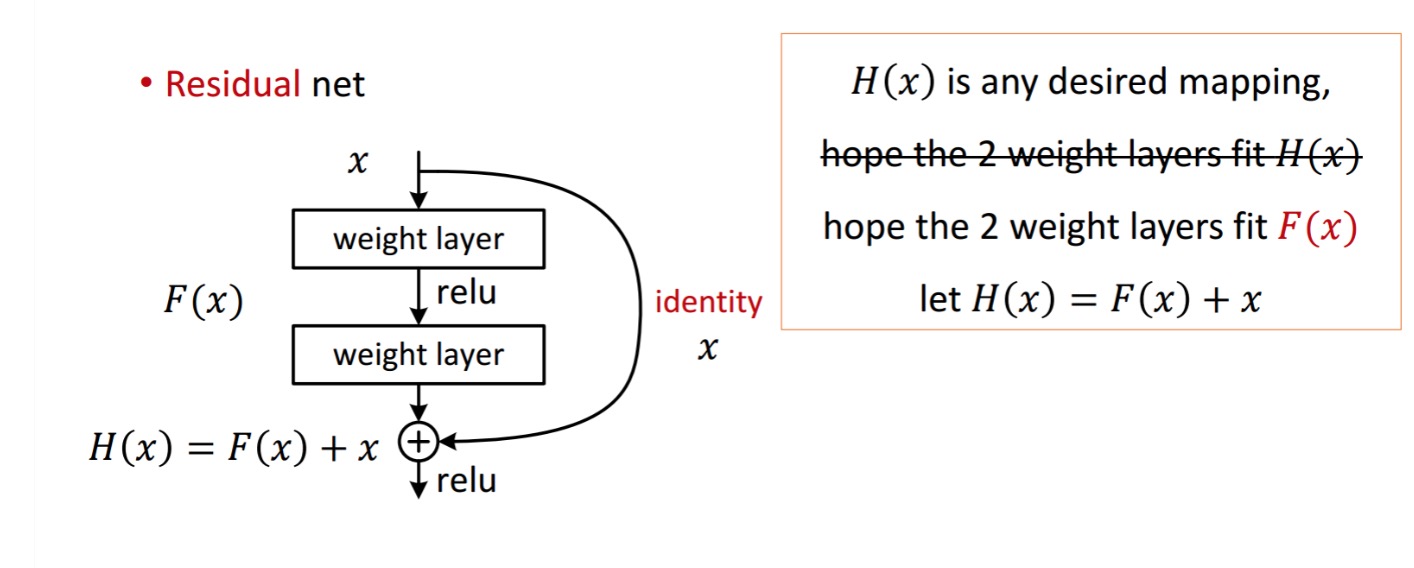
näin esitetty jäännösyksikkö saadaan käsittelemällä kahdella painokerroksella. Sitten se lisää saada . Nyt, oletetaan, että on ihanteellinen ennustettu tuotos, joka vastaa maa totuus. Koska saada haluttu riippuu saada täydellinen . Tämä tarkoittaa, että kaksi painokerrosta jäljellä yksikkö pitäisi todella pystyä tuottamaan haluttu, sitten saada ihanteellinen on taattu.

saadaan seuraavasti

saadaan seuraavasti

tekijät arvelevat, että jäännöskartoitus (eli ) saattaa olla helpompi optimoida kuin . Havainnollistaa yksinkertaisella esimerkillä, olettaa, että ihanteellinen . Sitten suora kartoitus olisi vaikea oppia identiteettikartoitus, koska on pino epälineaarisia kerroksia seuraavasti.

joten identiteetin kartoituksen likimääräistäminen kaikilla näillä painoilla ja Reluksilla keskellä olisi vaikeaa.

nyt, jos määrittelemme halutun kartoituksen , niin meidän tarvitsee vain saada seuraavasti.

edellä mainitun saavuttaminen on helppoa. Aseta mikä tahansa paino nollaan ja saat nollatuloksen. Lisää takaisin ja saat haluamasi kartoitus.

syvä Jälkioppiminen kuvantunnistukseen

ongelma

kun syvemmät verkot alkavat lähentyä, on paljastunut hajoamisongelma: verkon syvyyden kasvaessa tarkkuus kyllästyy ja heikkenee sitten nopeasti.

seeing Degrading in Action:

ottakaamme matala verkko ja sen syvempi vastine lisäämällä siihen useampia kerroksia.

pahimmassa tapauksessa: Deeper Modelin varhaiset kerrokset voidaan korvata shallow Networkilla ja jäljelle jääneet kerrokset voivat toimia vain identiteettifunktiona (Input equal to output).

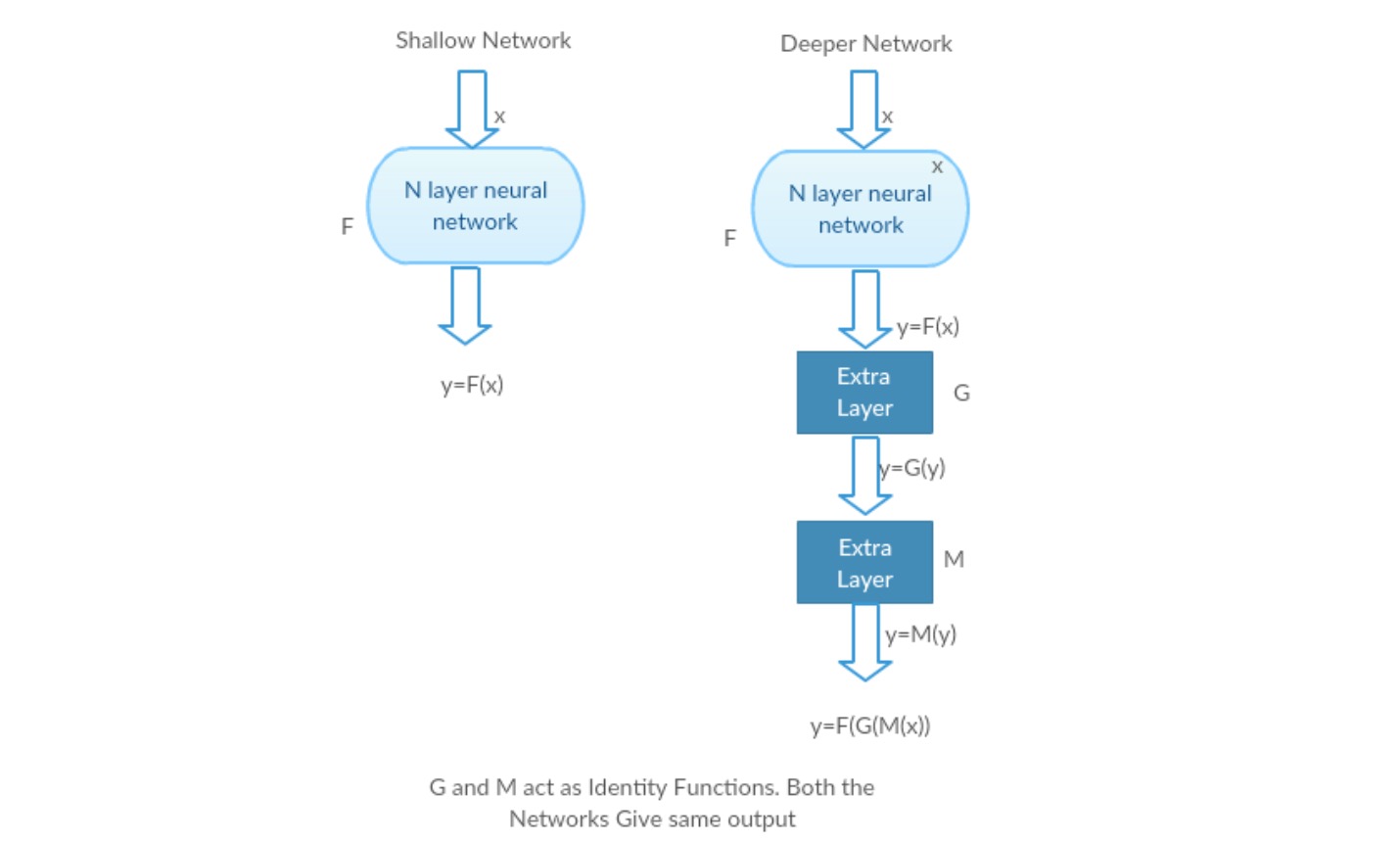
palkitseva skenaario: syvemmässä verkossa lisäkerrokset approksimoivat kartoitusta paremmin kuin sen matalampi laskuri-osa ja vähentävät virhettä merkittävällä marginaalilla.

Koe: Pahimmassa tapauksessa, sekä matala verkko ja syvempi variantti siitä pitäisi antaa sama tarkkuus. Palkitsevassa skenaariossa syvemmän mallin pitäisi antaa parempi tarkkuus kuin matalamman laskurin osan. Mutta kokeet nykyisillä ratkaisijoillamme paljastavat, että syvemmät mallit eivät suoriudu hyvin. Syvempien verkkojen käyttäminen siis heikentää mallin suorituskykyä. Nämä paperit yrittävät ratkaista tämän ongelman käyttämällä Deep jäännös learning framework.

miten ratkaista?

sen sijaan, että oppisi suoran kartoituksen funktiolla (muutama pinottu epälineaarinen kerros). Olkaamme määritellä jäljellä funktio käyttäen, joka voidaan reframed osaksi, jossa ja edustaa pinottu epälineaarisia kerroksia ja identiteetti funktio(input=output) vastaavasti.

kirjoittajan hypoteesi on, että jäännöskartoitustoiminto on helppo optimoida kuin alkuperäinen, viittaamaton kartoitus .

intuitio jäännöslohkojen takana:

otetaan esimerkiksi identiteettikartoitus (esim. Jos identiteetin kartoitus on optimaalinen, voimme helposti työntää jäännökset nollaan () kuin sovittaa identiteetin kartoitus () pinolla epälineaarisia kerroksia. Yksinkertaisella kielellä se on erittäin helppo keksiä ratkaisu kuin mieluummin kuin käyttämällä pinon epälineaarinen cnn kerrokset funktiona (ajattele sitä). Niin, tämä funktio on mitä kirjoittajat kutsutaan Jäännösfunktio.

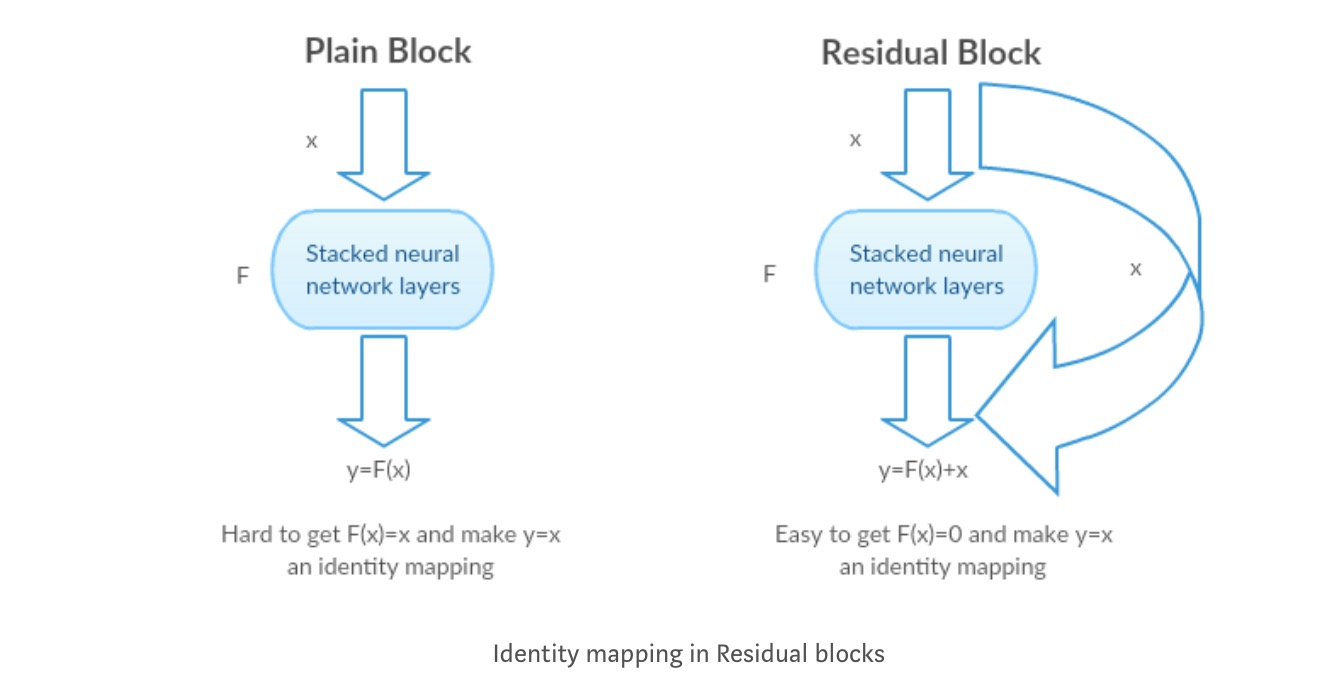
tekijät tekivät useita testejä hypoteesinsa testaamiseksi. Katsotaanpa niitä nyt.

testitapaukset:

otetaan tavallinen verkko (VGG kind 18 layer network) (Network-1) ja sen syvempi muunnos (34-layer, Network-2) ja lisätään jäljelle jäävät kerrokset Verkko-2: een (34-kerros jäännösliitännöineen, Network-3).

verkon suunnittelu:

1. käytä enimmäkseen 3*3 suodatinta.
2. Down sampling with CNN layers with stride 2.
3. Global average pooling layer ja 1000-tie täysin kytketty kerros Softmax lopussa.

on olemassa kahdenlaisia jäännösliittymiä:

I. identiteetin pikanäppäimiä () voidaan käyttää suoraan, kun Tulo () ja lähtö () ovat samankokoisia.

II. kun dimensiot muuttuvat, a) pikakuvake suorittaa edelleen identiteetin kartoituksen, jossa ylimääräiset nolla-merkinnät on pehmustettu suuremmalla ulottuvuudella. B) projektio-oikotietä käytetään vastaamaan ulottuvuutta (tehdään 1*1 conv: llä) seuraavalla kaavalla

tulokset

vaikka 18-kerroksinen verkko on vain aliavaruus 34-kerroksisessa verkossa, se toimii silti paremmin. ResNet päihittää merkittävän marginaalin, jos verkko on syvempi

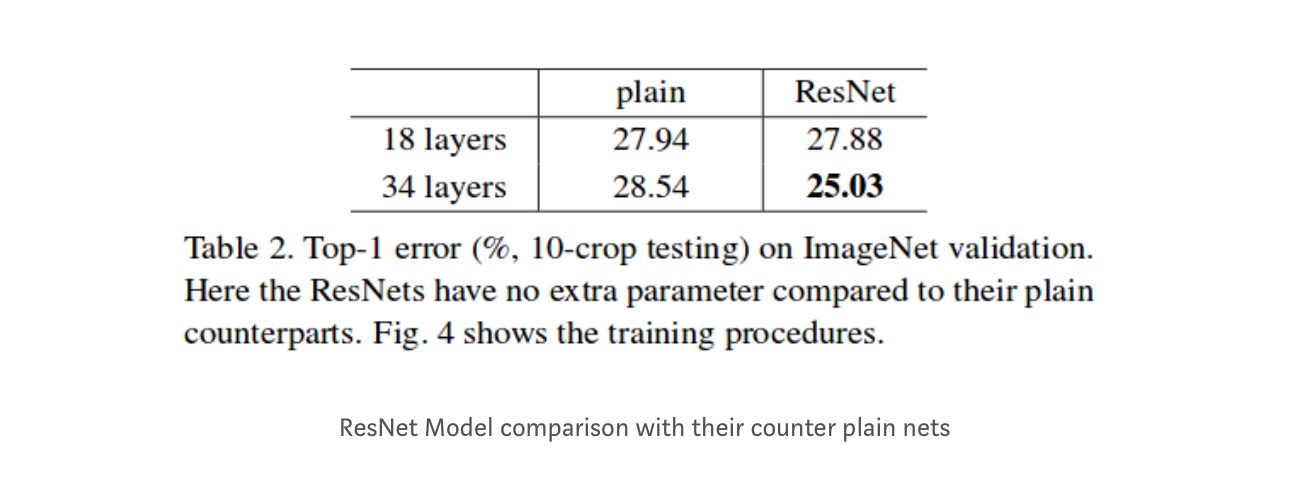
syvemmät tutkimukset

lisäksi tutkitaan enemmän verkkoja:

jokainen ResNet-lohko on joko 2-kerroksinen (käytetään pienissä verkoissa, kuten resnet 18, 34) tai 3 kerroksen syvyydessä( resnet 50, 101, 152).

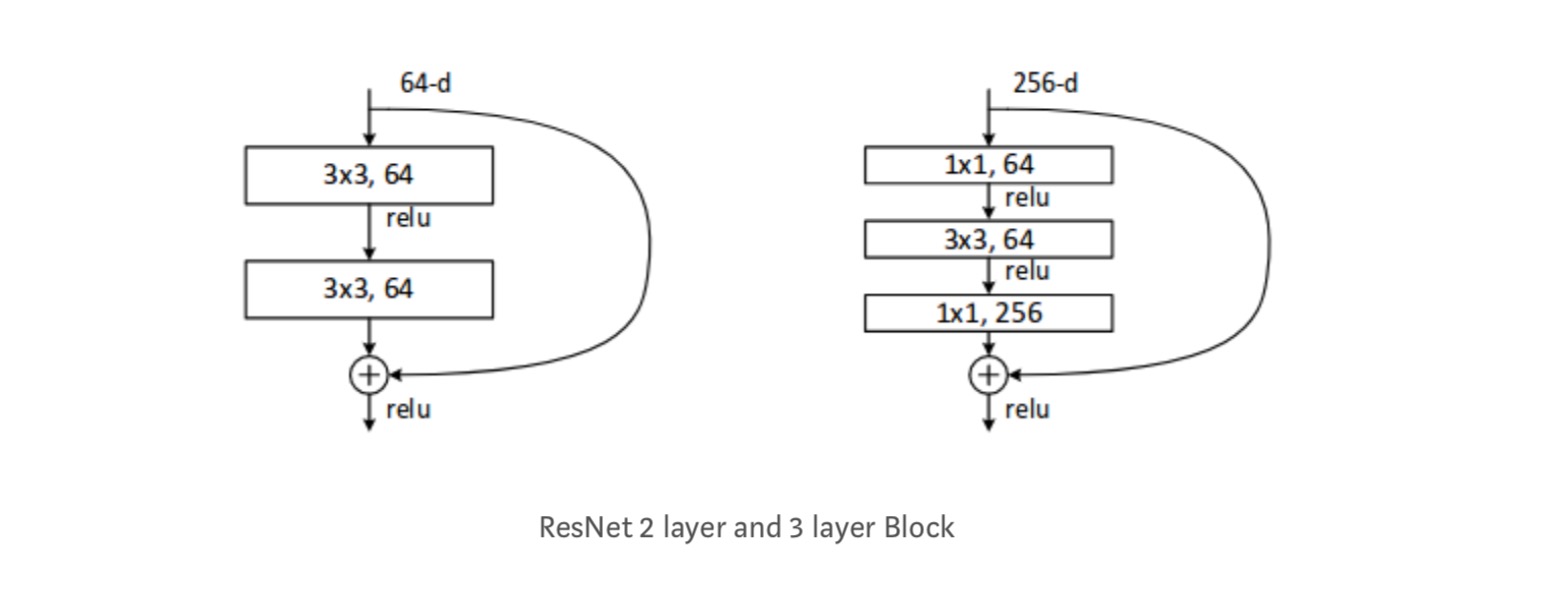
havainnot

1. ResNet-Verkko konvergoituu nopeammin kuin sen tavallinen vastaosa.
2. identiteetti vs. projektio shorcuts. Hyvin pieni inkrementaalinen voitot käyttäen projektio pikakuvakkeet (yhtälö-2) kaikissa kerroksissa. Joten kaikki ResNet-lohkot käyttävät vain identiteetin pikanäppäimiä projektioiden pikanäppäimiä käytetään vain, kun mitat muuttuvat.
3. ResNet-34 saavutti top-5-validointivirheen 5,71% paremmin kuin BN-inception ja VGG. ResNet-152: lla saavutetaan top-5-validointivirhe 4,49%. 6 eri syvyyksillä varustetun mallin kokonaisuudella saavutetaan top-5-validointivirhe 3,57%. 1. sijan voittaminen ILSVRC-2015: ssä

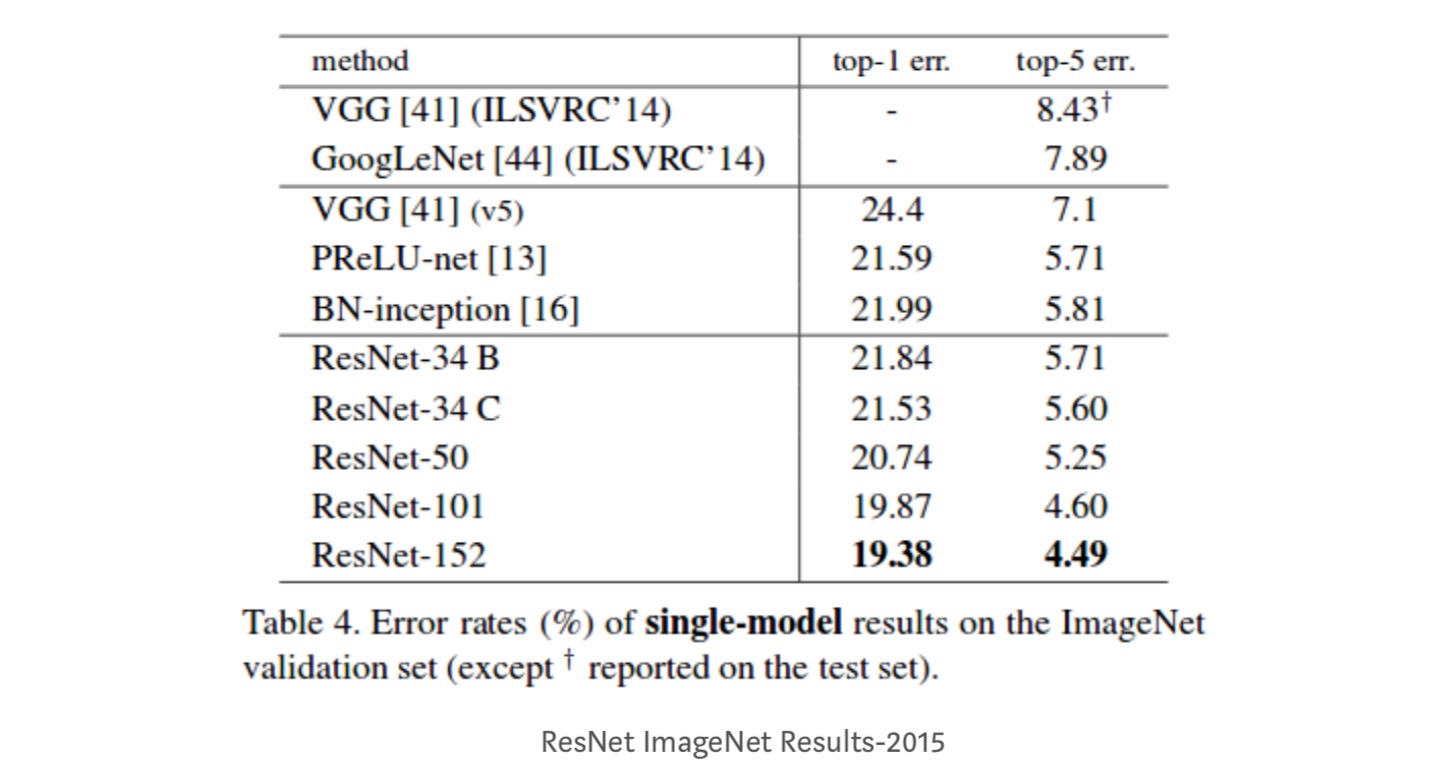
Identiteettikartoitukset syvissä Jäännösverkoissa

tämä paperi antaa teoreettisen käsityksen siitä, miksi katoava gradienttiongelma ei esiinny Jäännösverkoissa ja skip-yhteyksien rooli (skip-yhteydet tarkoittavat syöttöä tai ) korvaamalla Identity mapping (x) eri funktioilla.

Johdanto

syvät jäännösverkot koostuvat monista pinotuista ”Jäännösyksiköistä”. Jokainen yksikkö voidaan ilmaista yleisessä muodossa:

missä ja ovat yksikön Tulo ja tuotos, ja on jäännösfunktio. Viimeisessä paperissa on identiteetin kartoitus ja on ReLU-funktio.

Resnetien keskeinen ajatus on oppia additiivinen jäännösfunktio suhteessa , jossa on avainvalinta käyttää identiteettikartoitusta . Tämä toteutetaan liittämällä identity skip-yhteys (”oikotie”).

tässä artikkelissa analysoimme syviä jäännösverkostoja keskittymällä luomaan ”suoran” polun tiedon levittämiseen — ei vain jäännösyksikön sisällä, vaan koko verkon läpi. Meidän johdannaiset osoittavat, että jos molemmat ja ovat identiteetin kartoituksia, signaali voidaan suoraan lisätä yhdestä yksiköstä muihin yksiköihin, sekä eteen-ja taaksepäin kulkee. Kokeemme empiirisesti osoittavat, että koulutus yleensä helpottuu, kun arkkitehtuuri on lähempänä edellä mainittuja kahta ehtoa.

ymmärtääksemme skip-yhteyksien roolin analysoimme ja vertailemme erilaisia . Havaitsemme, että viimeisessä paperissa valitulla identiteetin kartoituksella saavutetaan nopein virhevähennys ja pienin harjoitushäviö kaikista tutkimistamme vaihtoehdoista, kun taas skaalaus -, gating-ja 1×1-konvoluutioiden ohitusliitännät johtavat kaikki suurempiin harjoitushäviöihin ja virheisiin. Nämä kokeet viittaavat siihen, että pitää ”puhdas” informaatiopolku on hyödyllistä helpottaa optimointia.

identiteetin kartoituksen muodostamiseksi näemme aktivointifunktiot (ReLU ja BN) painokerrosten ”esiaktivaationa”, toisin kuin tavanomainen ”jälkiaktivaation”viisaus. Tämä näkökulma johtaa uuden jäännösyksikön suunnitteluun, joka on esitetty seuraavassa kuvassa. Tämän yksikön perusteella esitämme kilpailukykyisiä tuloksia CIFAR-10/100: ssa 1001-kerroksisella ResNet: lla, joka on paljon helpompi kouluttaa ja yleistää paremmin kuin alkuperäinen ResNet. Lisäksi raportoimme parannetuista tuloksista Imagenetissä käyttäen 200-kerroksista Resnettiä,jonka vastine viimeiselle paperille alkaa ylittämään. Tulokset viittaavat siihen, että on paljon tilaa hyödyntää verkon syvyyden ulottuvuutta, joka on avain nykyaikaisen syväoppimisen onnistumiseen.

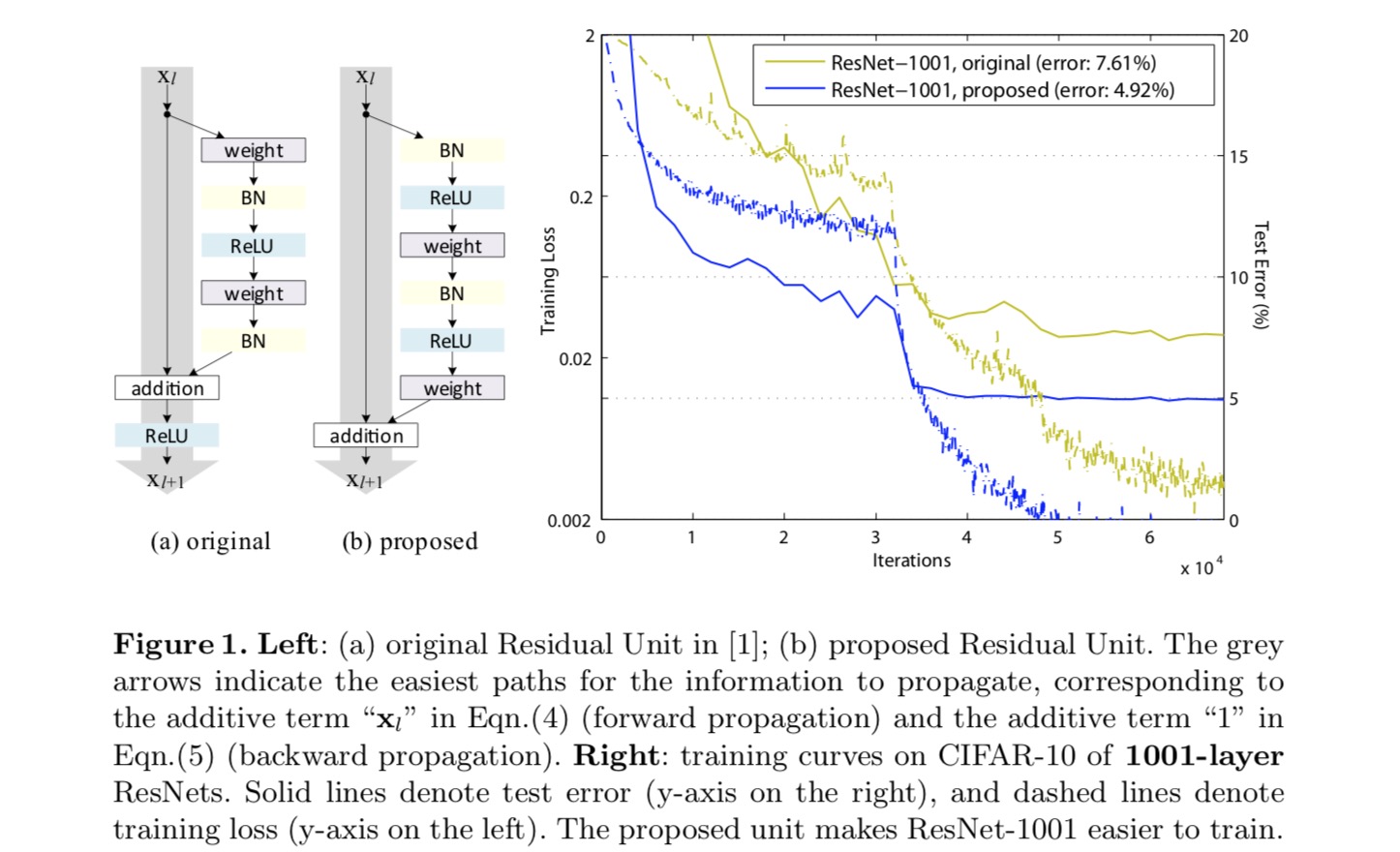
syvien Jäännösverkkojen analysointi

viimeisessä paperissa kehitetyt Resnetit ovat modularisoituja arkkitehtuureja, jotka pinoavat saman liitosmuotoisia rakennuspalikoita. Tässä asiakirjassa kutsumme näitä lohkoja ”Jäännösyksiköiksi”. Alkuperäinen Jäännösyksikkö viimeisessä paperissa suorittaa seuraavan laskutoimituksen:

tässä on syöte ominaisuus-TH Jäännösyksikköön. on joukko painot ( ja harhat) liittyvät-TH jäljellä yksikkö, ja on kerrosten määrä on jäljellä yksikkö (on 2 tai 3 viimeisessä paperi). tarkoittaa jäännösfunktiota, e.g., pino kaksi 3×3 convolutionary kerrosta viimeinen paperi. Funktio on operaatio elementtikohtaisen yhteenlaskun jälkeen, ja viimeisessä paperissa on ReLU. Funktio asetetaan identiteettikartoitukseksi:.

If on myös identiteetin kartoitus: , voimme saada:

rekursiivisesti meillä on:

mille tahansa syvemmälle yksikölle ja mille tahansa matalammalle yksikölle . Tämä yhtälö osoittaa joitakin mukavuusominaisuuksia. (1) ominaisuus tahansa syvempi yksikkö voidaan esittää ominaisuus tahansa matalampi yksikkö plus jäljellä funktio muodossa , mikä osoittaa, että malli on jäljellä tavalla välillä mitään yksiköitä ja . (2) ominaisuus , tahansa syvä yksikkö , on yhteenlasku lähdöt kaikkien edeltävien jäljellä toimintoja (plus). Tämä on vastakohta ”tavalliselle verkolle”, jossa ominaisuus on sarja matriisivektorituotteita, vaikkapa (sivuuttaen BN: n ja Relun).

yllä oleva yhtälö johtaa myös mukaviin taaksepäin etenemisominaisuuksiin. Häviöfunktiota merkitään vastapropagaation ketjusäännöstä seuraavasti:

yllä oleva yhtälö osoittaa, että gradientti voidaan hajottaa kahdeksi additiiviseksi termiksi: termi, joka lisää tietoa suoraan käsittelemättä mitään painokerroksia, ja toinen termi, joka etenee painokerrosten kautta. Lisäainetermillä varmistetaan, että tiedot lisätään suoraan matalampaan yksikköön l. yllä oleva yhtälö viittaa myös siihen, että on epätodennäköistä, että gradienttia kumottaisiin minierän osalta, koska yleensä termi ei voi aina olla -1 kaikkien minierän näytteiden osalta. Tämä tarkoittaa, että kerroksen gradientti ei katoa, vaikka painot olisivat mielivaltaisen pieniä.

edellä mainitut kaksi yhtälöä viittaavat siihen, että signaali voidaan suoraan levittää mistä tahansa yksiköstä toiseen, sekä eteen-että taaksepäin. Perusta ensimmäisen edellä kaksi yhtälöä on kaksi identiteetti Kuvaukset: (1) identiteetti ohita yhteys , ja (2) ehto, joka on identiteetti kartoitus.

identiteetin ohitusliittymien tärkeys

tarkastellaan yksinkertaista muunnosta, , identiteetin oikotien katkaisemiseksi:

missä on moduloiva skalaari (yksinkertaisuuden vuoksi oletamme edelleen identiteetiksi). Rekursiivisesti soveltamalla tätä muotoilua saamme yhtälö samanlainen kuin edellä:

, jossa notaatio absorboi skalaarit jäljelle jääviin funktioihin. Vastaavasti meillä on backpropagaatio seuraavassa muodossa:

toisin kuin edellisessä yhtälössä, tässä yhtälössä ensimmäistä additiivista termiä moduloidaan kertoimella . Erittäin syvä verkko (on suuri), jos kaikille , tämä tekijä voi olla eksponentiaalisesti suuri; jos kaikille , tämä tekijä voi olla eksponentiaalisesti pieni ja kadota, joka estää backropagated signaalin pikakuvakkeen ja pakottaa sen virtaamaan läpi painokerrokset. Tämä johtaa optimointivaikeuksiin, kuten kokeet osoittavat.

yllä olevassa analyysissä alkuperäinen identiteetin ohitusliitäntä korvataan yksinkertaisella skaalauksella . Jos skip-yhteys edustaa monimutkaisempia muunnoksia (kuten gating ja 1×1 convolutions), edellä yhtälössä ensimmäinen termi tulee Missä on derivaatta,. Tämä tuote voi myös haitata tiedon levittämistä ja vaikeuttaa koulutusta, kuten seuraavissa kokeissa on todettu.

kokeet Skip-yhteyksillä

kokeillaan 110-kerroksista Resnettiä cifar-10: ssä. Tässä erittäin syvässä ResNet-110: ssä on 54 kaksikerroksista Jäännösyksikköä (joka koostuu 3×3 convolutionaalikerroksesta) ja on haastava optimoinnin kannalta. Erilaisia ohitusyhteyksiä kokeillaan. Katso seuraava kuva:

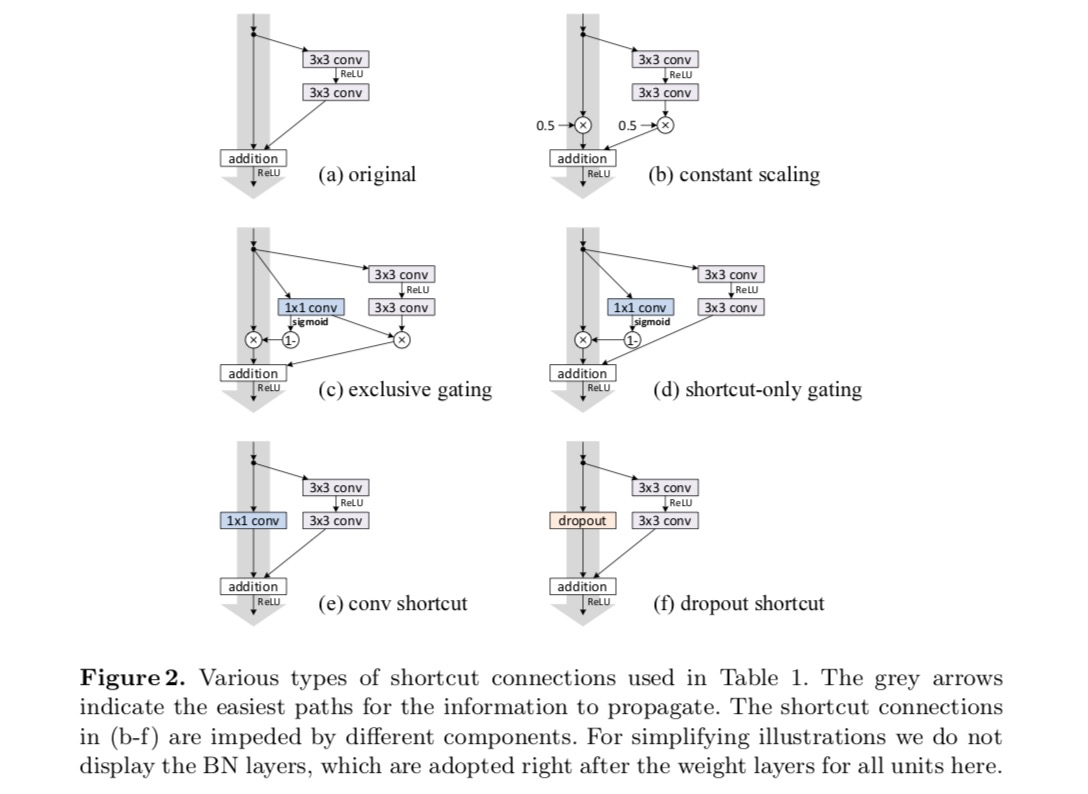
luokitustulokset näkyvät seuraavassa taulukossa:

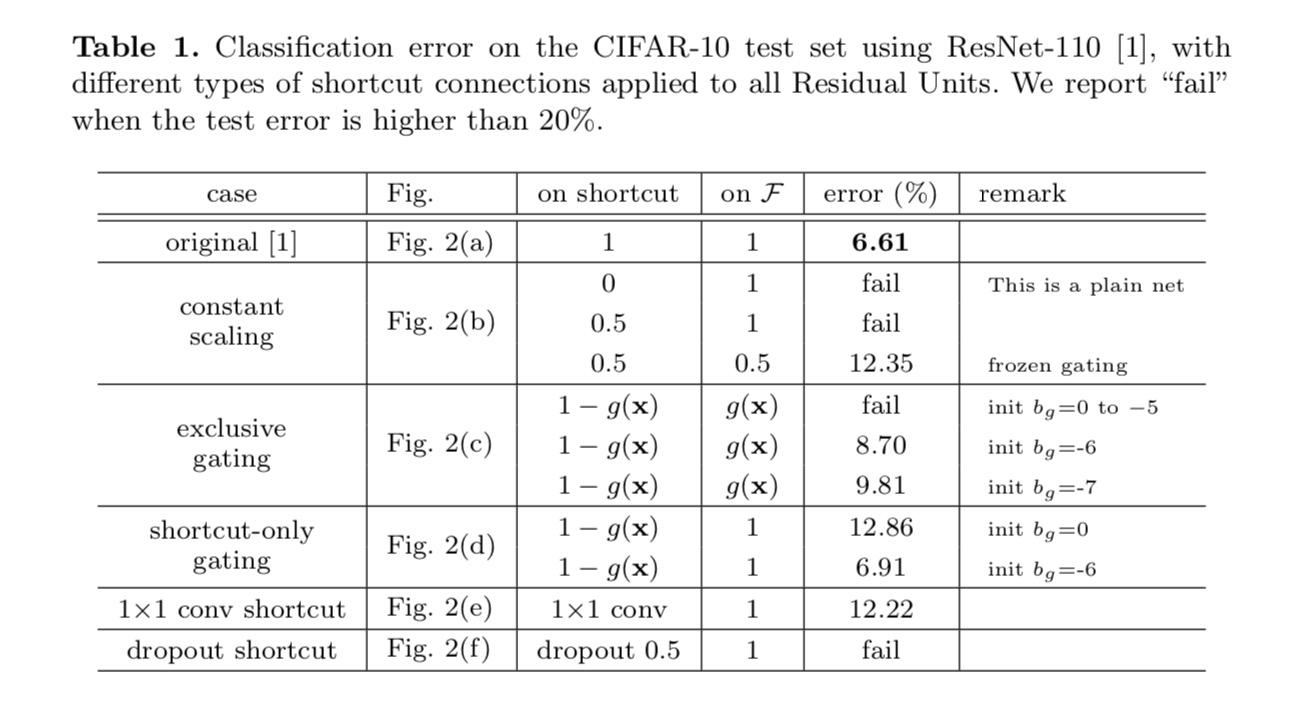
kuten yllä olevan kuvan harmaat nuolet osoittavat, oikotieyhteydet ovat suorimpia väyliä tiedon levittämiseen. Kertova manipulointi (skaalaus, gating, 1×1 convolutions, ja dropout) pikakuvakkeet voivat haitata tiedon leviämistä ja johtaa optimointiongelmiin.

on huomionarvoista, että gating-ja 1×1 convolutionaaliset pikanäppäimet tuovat enemmän parametreja, ja niillä pitäisi olla vahvemmat representaatiokyvyt kuin identiteettinäppäimillä. Itse asiassa, pikakuvake-vain gating ja 1×1 konvoluutio kattavat ratkaisu tilaa identity pikanäppäimet (toisin sanoen, ne voitaisiin optimoida identity pikanäppäimet). Niiden koulutusvirhe on kuitenkin suurempi kuin identiteetin oikoteillä, mikä viittaa siihen, että näiden mallien hajoaminen johtuu optimointikysymyksistä representaatiokyvyn sijaan.

Aktivointifunktioiden käyttö

yllä olevassa jaksossa tehdyt kokeet oletetaan, että lisäyksen jälkeinen aktivaatio on identiteetin kartoitus. Mutta edellä kokeissa on ReLU suunniteltu ensimmäisen paperin. Seuraavaksi tutkitaan vaikutusta .

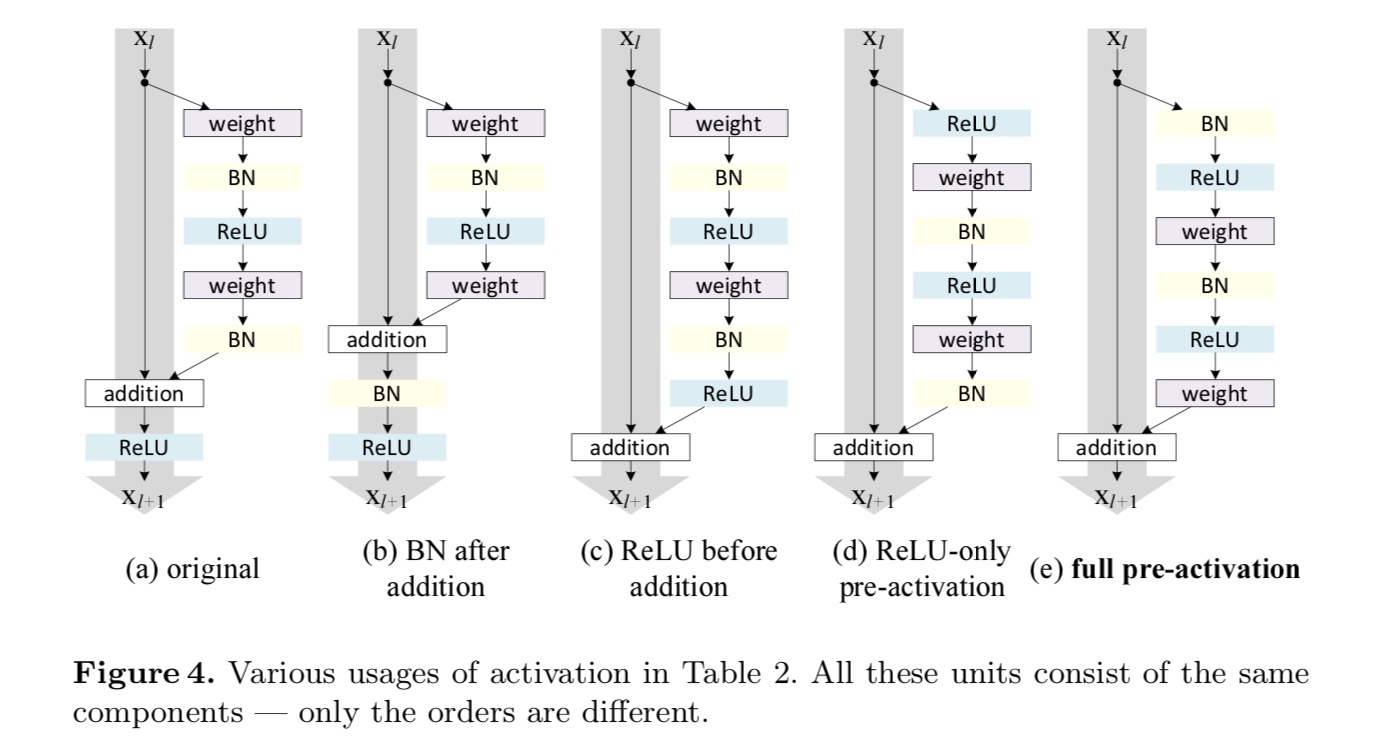
haluamme tehdä identiteettikartoituksen, joka tehdään järjestämällä aktivointifunktiot uudelleen (ReLU ja / tai BN, erän normalisointi). Seuraavassa kuvassa viimeisen paperin alkuperäinen Jäännösyksikkö on muodoltaan viikuna. 4 (a) – BN käytetään jokaisen painokerroksen jälkeen, ja ReLU hyväksytään BN: n jälkeen, paitsi että viimeinen ReLU Jäännösyksikössä on elementwise addition jälkeen ( = ReLU). Kuva. 4 (b-e) Näytä tutkimamme vaihtoehdot.

Aktivointikokeet

tässä osiossa kokeillaan ResNet-110: tä ja 164-kerroksista Pullonkaulaarkkitehtuuria (merkitään ResNet-164: llä). Pullonkaula jäljellä yksikkö koostuu 1×1 kerros vähentää Ulottuvuus, 3×3 kerros, ja 1×1 kerros palauttaa ulottuvuus. Kuten suunniteltu viimeinen paperi, sen laskennallinen monimutkaisuus on samanlainen kuin kaksi-3×3 jäljellä yksikkö.

aktivoinnin jälkeen vai ennen aktivointia?

alkuperäisessä suunnitelmassa aktivaatio vaikuttaa molempiin polkuihin seuraavassa Jäännösyksikössä: . Seuraavaksi kehitämme epäsymmetrisen muodon, jossa aktivointi vaikuttaa vain polkuun:, kaikille . Nimeämällä notaatiot uudelleen saadaan seuraava muoto:

tälle uudelle Jäännösyksikölle kuten yllä olevassa yhtälössä, Uusi additioaktivaatio muuttuu identiteettikartoitukseksi. Tämä rakenne tarkoittaa sitä, että jos Uusi additioaktivaatio otetaan epäsymmetrisesti käyttöön, se vastaa uudelleenlastausta seuraavan Jäännösyksikön esiaktivaationa. Tämä näkyy seuraavassa kuvassa:

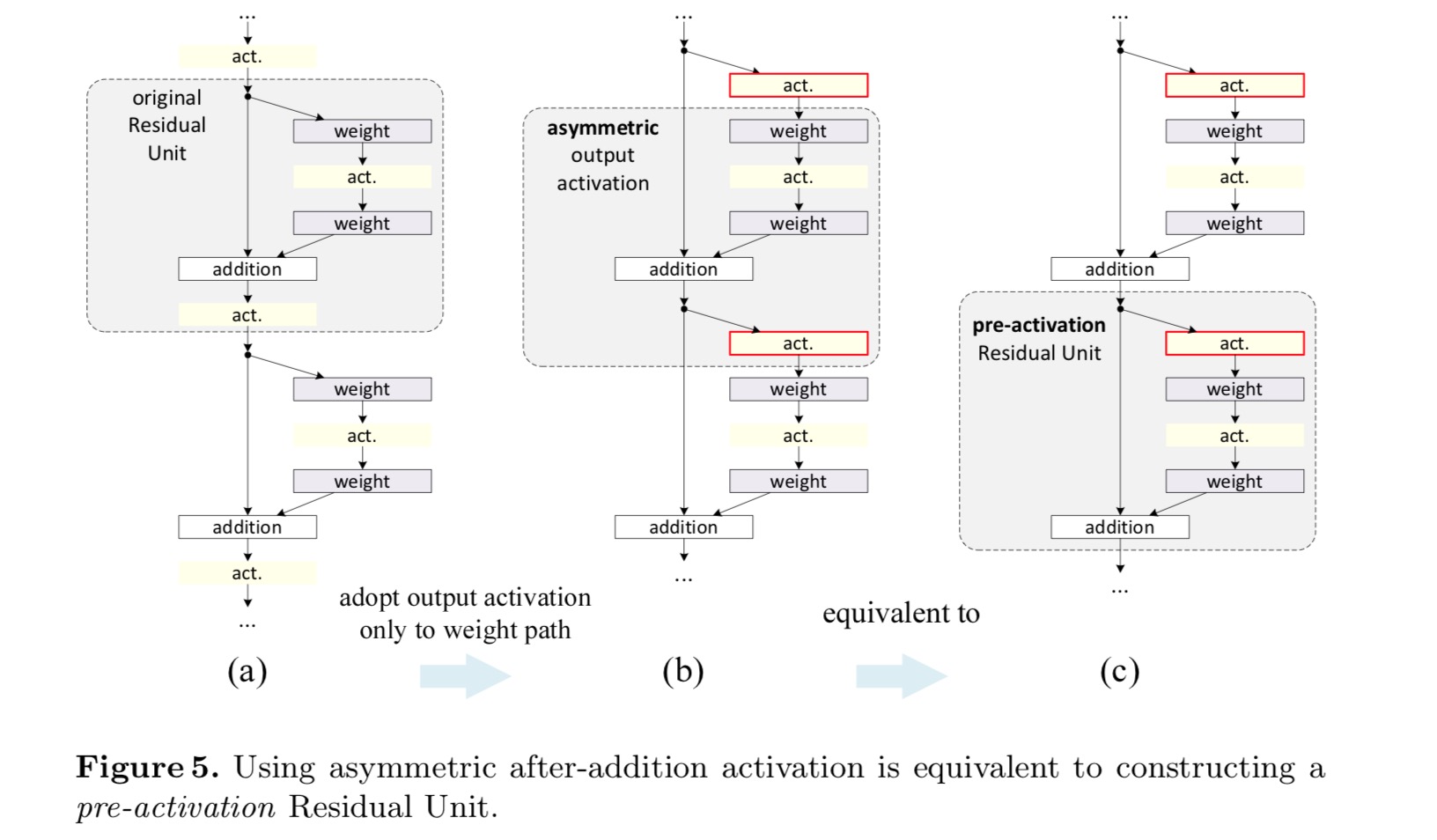
ero jälkiaktivaation / esiaktivaation välillä johtuu alkuaineliitoksen läsnäolosta. Tavalliselle verkolle, jossa on n − kerroksia, on olemassa N – 1-aktivaatioita (BN/ReLU), eikä ole väliä, pidämmekö niitä jälki-vai esiaktivaatioina. Mutta haarautuneille kerroksille, jotka yhdistyvät yhteenlaskulla, aktivaation sijainnilla on merkitystä. Aktivoinnin eri käyttötavat esitetään kuvassa 4.

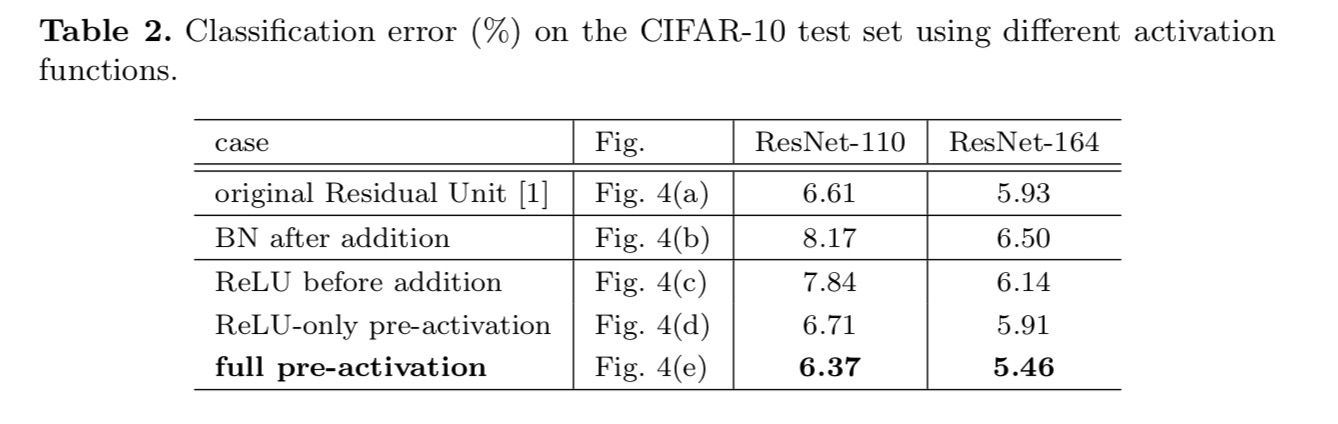
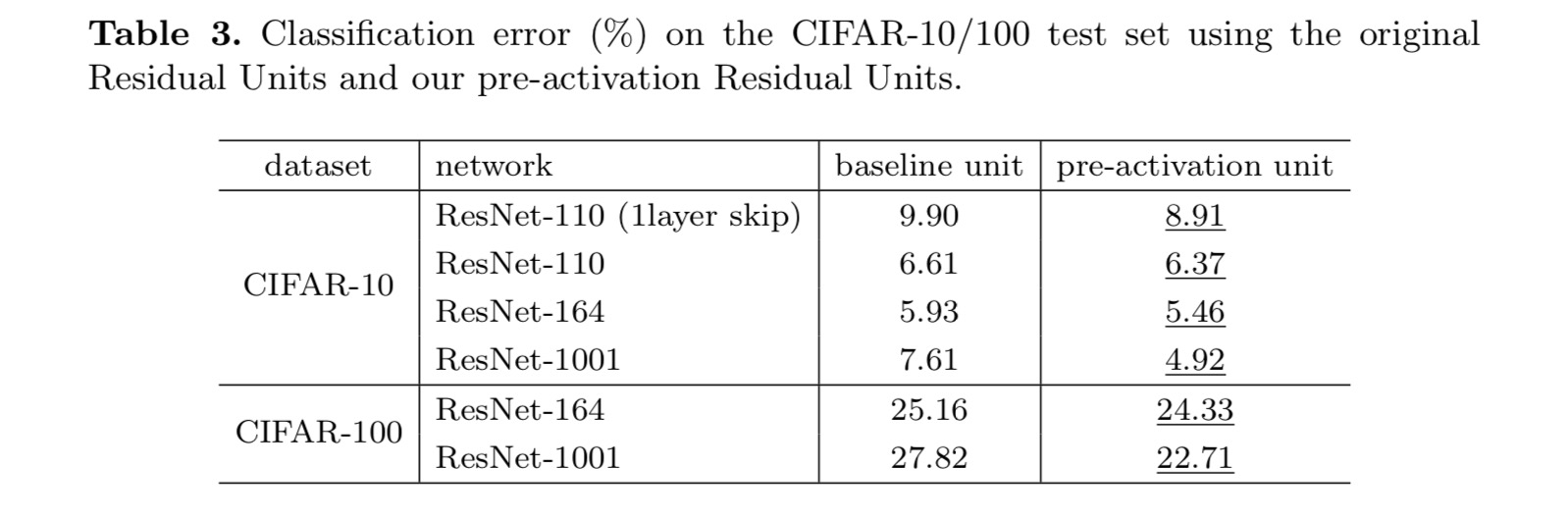
kokeillaan kahta tällaista mallia: (1) ReLU-vain pre-aktivointi ja (2) täydellinen pre-aktivointi, jossa BN ja ReLU molemmat hyväksytään ennen painokerroksia. Jotenkin yllättäen, kun sekä BN että ReLU käytetään pre-aktivaationa, tulokset paranevat terveillä marginaaleilla

huomaamme esiaktivaation vaikutuksen olevan kaksijakoinen. Ensinnäkin optimointia helpotetaan edelleen (vertaamalla perustason Resnettiin), koska f on identiteetin kartoitus. Toiseksi BN: n käyttäminen esiaktivointina parantaa mallien säännönmukaistamista.

Conclusion

tämä paperi tutkii syvien jäännösverkkojen kytkentämekanismien taustalla olevia etenemismuotoja. Meidän johdannaiset tarkoittavat, että identiteetti oikosulku yhteydet ja identiteetti jälkeen lisäys aktivointi ovat välttämättömiä tehdä tiedon eteneminen sujuvaa. Ablaatio kokeet osoittavat phenom-ena, jotka ovat yhdenmukaisia meidän johdannaiset. Esittelemme myös 1000-kerroksisia syväverkkoja, joita on helppo kouluttaa ja parantaa tarkkuutta.

syvien neuroverkkojen yhdistetyt Jäännösmuunnokset

Johdanto

visuaalisen tunnistuksen tutkimus on siirtymässä ”feature Engineeringistä” ”network engineeringiin”. Inhimillinen panostus on siirtynyt parempien verkkoarkkitehtuurien suunnitteluun oppimisesityksiä varten.

arkkitehtuurien suunnittelu käy yhä vaikeammaksi hyper-parametrien määrän kasvaessa erityisesti silloin, kun kerroksia on paljon. VGG-nets-hankkeessa on yksinkertainen mutta tehokas strategia erittäin syvien verkkojen rakentamiseksi: samanmuotoisten rakennuspalikoiden pinoaminen. Tämä strategia periytyy Resneteillä, jotka pinoavat saman topologian moduuleja. Tämä yksinkertainen sääntö vähentää hyper-parametrien vapaita valintoja, ja syvyys paljastuu olennaiseksi ulottuvuudeksi neuroverkoissa. Lisäksi väitämme, että tämän säännön yksinkertaisuus voi vähentää riskiä, että hyperparametrit mukautuvat liikaa tiettyyn aineistoon. VGG-verkkojen ja Resnetien kestävyys on osoitettu erilaisilla visuaalisilla tunnistustehtävillä sekä ei-visuaalisilla tehtävillä, joihin liittyy puhe ja kieli.

toisin kuin VGG-nets, Inception-mallien perhe on osoittanut, että huolellisesti suunnitelluilla topologioilla voidaan saavuttaa pakottava tarkkuus matalalla teoreettisella kompleksisuudella. Inception-mallit ovat kehittyneet ajan myötä, mutta tärkeä yhteinen ominaisuus on split-transform-merge-strategia. In Inception module, tulo on jaettu muutaman alemman ulotteinen embeddings (by 1×1 convolutions), muunnetaan joukko erikoistuneita suodattimia (3×3, 5×5, jne.), ja yhdistettiin concatenation. Aloitusmoduulien split-transform-merge-käyttäytymisen odotetaan lähestyvän suurten ja tiheiden kerrosten esitystehoa, mutta huomattavasti pienemmällä laskennallisella kompleksisuudella.

hyvästä tarkkuudesta huolimatta Inception-mallien toteutumiseen on liittynyt joukko mutkistavia tekijöitä. Vaikka näiden komponenttien huolelliset yhdistelmät tuottavat erinomaisia neuroverkkoreseptejä, on yleisesti epäselvää, miten Alkuarkkitehtuurit sovitetaan uusiin tietokokonaisuuksiin/tehtäviin, varsinkin kun on monia tekijöitä ja hyper-parametreja suunniteltavana.

tässä asiakirjassa esittelemme yksinkertaisen arkkitehtuurin, joka noudattaa VGG / Resnetsin toistuvien kerrosten strategiaa, samalla kun hyödynnämme split-transform-merge-strategiaa helpolla, laajennettavalla tavalla. Verkkoomme kuuluva moduuli suorittaa joukon muunnoksia, joista jokainen on pieniulotteinen embedding, jonka tuotokset kootaan yhteen summaamalla. Tavoittelemme tämän ajatuksen yksinkertaista toteutumista — koottavat muunnokset ovat kaikki samaa topologiaa. Tämä muotoilu antaa meille mahdollisuuden laajentaa mihin tahansa suureen määrään muutoksia ilman erikoistuneita malleja.

osoitamme empiirisesti, että aggregoidut muunnoksemme päihittävät Alkuperäisen ResNet-moduulin, vaikka laskennallisen monimutkaisuuden ja mallikoonkin säilyttäminen olisi rajoitettua. Korostamme, että vaikka tarkkuutta on suhteellisen helppo lisätä kapasiteettia lisäämällä (syvemmällä tai laajemmalla), menetelmät, jotka lisäävät tarkkuutta säilyttäen (tai vähentäen) monimutkaisuutta, ovat harvinaisia kirjallisuudessa.

menetelmämme osoittaa, että kardinaalisuus (muunnosjoukon koko) on leveys-ja syvyysmittojen lisäksi konkreettinen, mitattavissa oleva ulottuvuus, jolla on keskeinen merkitys. Kokeet osoittavat, että kardinaalisuuden lisääminen on tehokkaampi tapa saada tarkkuutta kuin syvemmälle tai laajemmalle meneminen, varsinkin kun syvyys ja leveys alkavat antaa pieneneviä tuottoja nykyisille malleille.

neuroverkkomme, nimeltään ResNeXt (mikä viittaa seuraavaan ulottuvuuteen), päihittävät Imagenetin luokitustietokannassa ResNet-101/152, ResNet-200, Inception-v3 ja Inception-ResNet-v2. Erityisesti 101-kerroksinen ResNeXt pystyy saavuttamaan paremman tarkkuuden kuin ResNet-200, mutta sen monimutkaisuus on vain 50%. Lisäksi ResNeXt esittelee huomattavasti yksinkertaisempia malleja kuin kaikki Inception-mallit.

menetelmä

otamme käyttöön erittäin modulaarisen mallin VGG / Resnetsin jälkeen. Verkostomme koostuu pinosta jäljellä olevia lohkoja. Näillä lohkoilla on sama topologia, ja niihin sovelletaan kahta yksinkertaista sääntöä, jotka perustuvat VGG/Resneteihin: (1) jos laaditaan samankokoisia paikkatietokarttoja, lohkoilla on samat hyper-parametrit (leveys ja suodatinkoot), ja (2) joka kerta, kun paikkatietokarttaa otetaan alaspäin kertoimella 2, lohkojen leveys kerrotaan kertoimella 2. Toinen sääntö varmistaa, että laskennallinen monimutkaisuus, kannalta FLOPs (liukulukutoiminnot, in #Of moninkertaistaa-lisää), on suurin piirtein sama kaikille lohkoille.

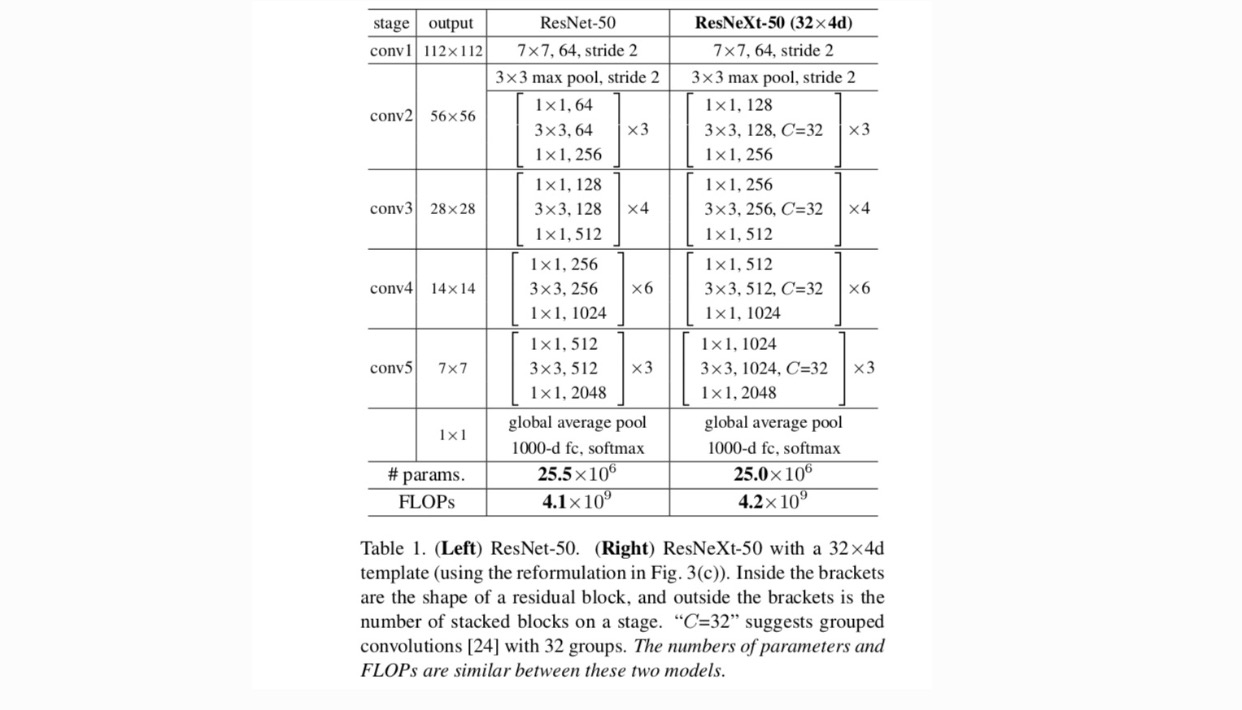
näillä kahdella säännöllä meidän tarvitsee vain suunnitella mallimoduuli, ja kaikki verkon moduulit voidaan määrittää sen mukaisesti. Joten nämä kaksi sääntöä kaventavat huomattavasti suunnittelutilaa ja antavat meille mahdollisuuden keskittyä muutamaan avaintekijään. Näillä säännöillä rakennetut verkot esitetään taulukossa 1.

keinotekoisten neuroverkkojen yksinkertaisimmat hermosolut suorittavat sisätuloa (painotettua summaa), joka on täysin toisiinsa kytkeytyvien ja convolutionaaristen kerrosten tekemä alkeismuunnos.

edellä mainittu operaatio voidaan esittää uudelleen jakamisen, muuntamisen ja aggregoinnin yhdistelmänä. (1): Splitting: vektori on viipaloitu kuin low-dimensional embedding, ja edellä, se on yhden ulottuvuuden aliavaruus (2) Transforming: low-dimensional representation on muunnettu, ja edellä, se on yksinkertaisesti skaalattu: (3) Aggregating: transformations kaikissa embeddings ovat aggregated .

ottaen huomioon edellä esitetyn yksinkertaisen neuronin analyysin, harkitsemme alkeiskonformaation (w_i, x_i) korvaamista yleisemmällä funktiolla, joka itsessään voi olla myös verkko. Muodollisesti esitämme aggregoidut muunnokset seuraavasti:

missä voi olla mielivaltainen funktio. Analoginen yksinkertainen neuroni, pitäisi projisoida (valinnaisesti matala-ulotteinen) upottaminen ja sitten muuttaa sitä.

kutsumme sitä kardinaaliudeksi. on asemassa samanlainen kuin vuonna, mutta ei tarvitse yhtä ja voi olla mielivaltainen määrä. Osoitamme kokeilla, että kardinaalisuus on olennainen ulottuvuus ja voi olla tehokkaampi kuin leveyden ja syvyyden mitat.

tässä asiakirjassa pidämme yksinkertainen tapa suunnitella transformaatio toiminnot: Kaikki ’s on sama topologia. Tämä laajentaa VGG-tyylistä strategiaa, jossa toistuvat saman muotoiset kerrokset. Asetimme yksittäisen muutoksen olevan pullonkaulan muotoinen arkkitehtuuri kuvitettu Fig. 1 (oikealla). Tällöin ensimmäinen 1×1 kerros kussakin tuottaa pieniulotteisen upotuksen.

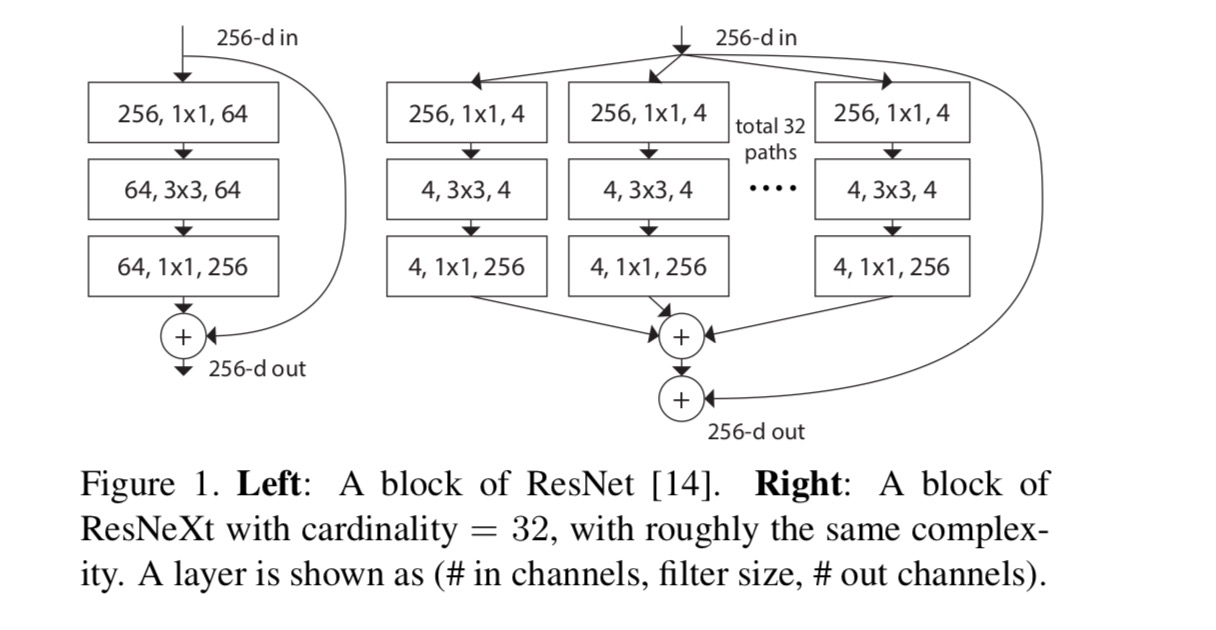
viimeisen yhtälön aggregoitu muunnos toimii jäännösfunktiona:

missä on lähtö.

Resnextin ja Inception-ResNet/Grouped-Convolutions väliset suhteet on esitetty seuraavassa kuvassa:

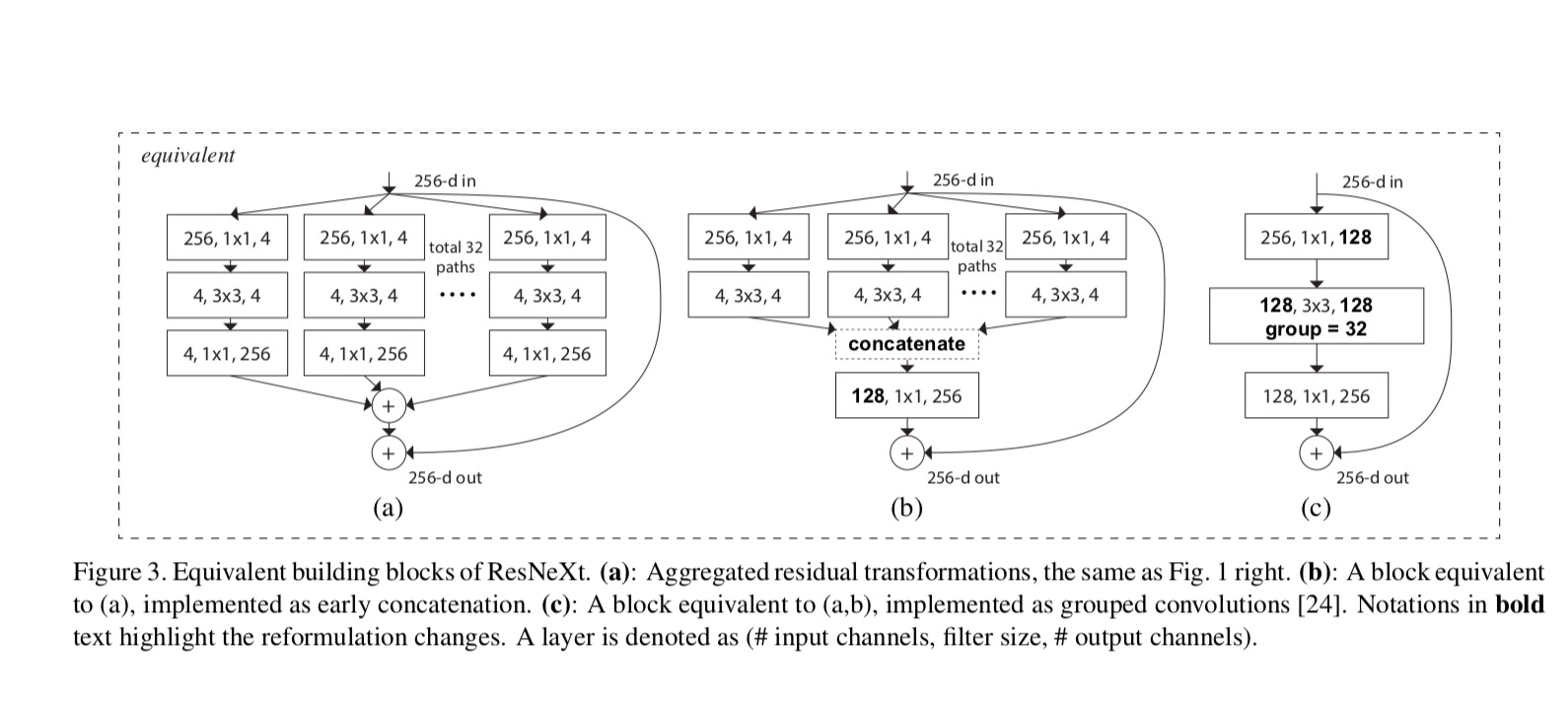
kun arvioimme erilaisia kardinaliteetteja säilyttäen kompleksisuuden, haluamme minimoida muiden hyper-parametrien modifioinnin. Päätämme säätää pullonkaulan leveyttä(esim.4-d kuvassa 1 (oikealla)), koska se voidaan eristää lohkon syötteestä ja ulostulosta. Tämä strategia tuo mitään muutosta muihin hyper-parametrit (syvyys tai tulo/lähtö leveys lohkojen), joten on hyödyllistä, että voimme keskittyä vaikutus kardinaalisuuden.

viikuna. 1 (vasemmalla), alkuperäinen ResNet pullonkaula lohko on parametrit ja suhteellinen floppeja (on sama ominaisuus kartan koko). Pullonkaulan leveys, meidän malli Kuvassa. 1 (Oikealla) on: parametrit ja suhteellinen floppeja. Kun Ja, tämä numero . Seuraava taulukko osoittaa kardinaalisuuden ja pullonkaulan leveyden välisen suhteen .

kokeet

Kardinaalisuus vs. leveys. Ensin arvioidaan kardinaalisuuden ja pullonkaulan leveyden välinen kompromissi taulukossa 2 esitetyllä tavalla. Tulokset esitetään taulukossa 3. Verrattuna ResNet-50, 32×4D ResNeXt-50 on validointivirhe 22.2%, joka on 1.7% pienempi kuin ResNet perustason 23.9%. Kun kardinaalisuus kasvaa 1: stä 32: een säilyttäen monimutkaisuuden, virhetaso laskee jatkuvasti. Lisäksi 32×4D Resnextissä on myös paljon pienempi harjoitusvirhe kuin ResNet countetpartissa, mikä viittaa siihen, että voitot eivät johdu laillistamisesta vaan vahvemmista representaatioista.

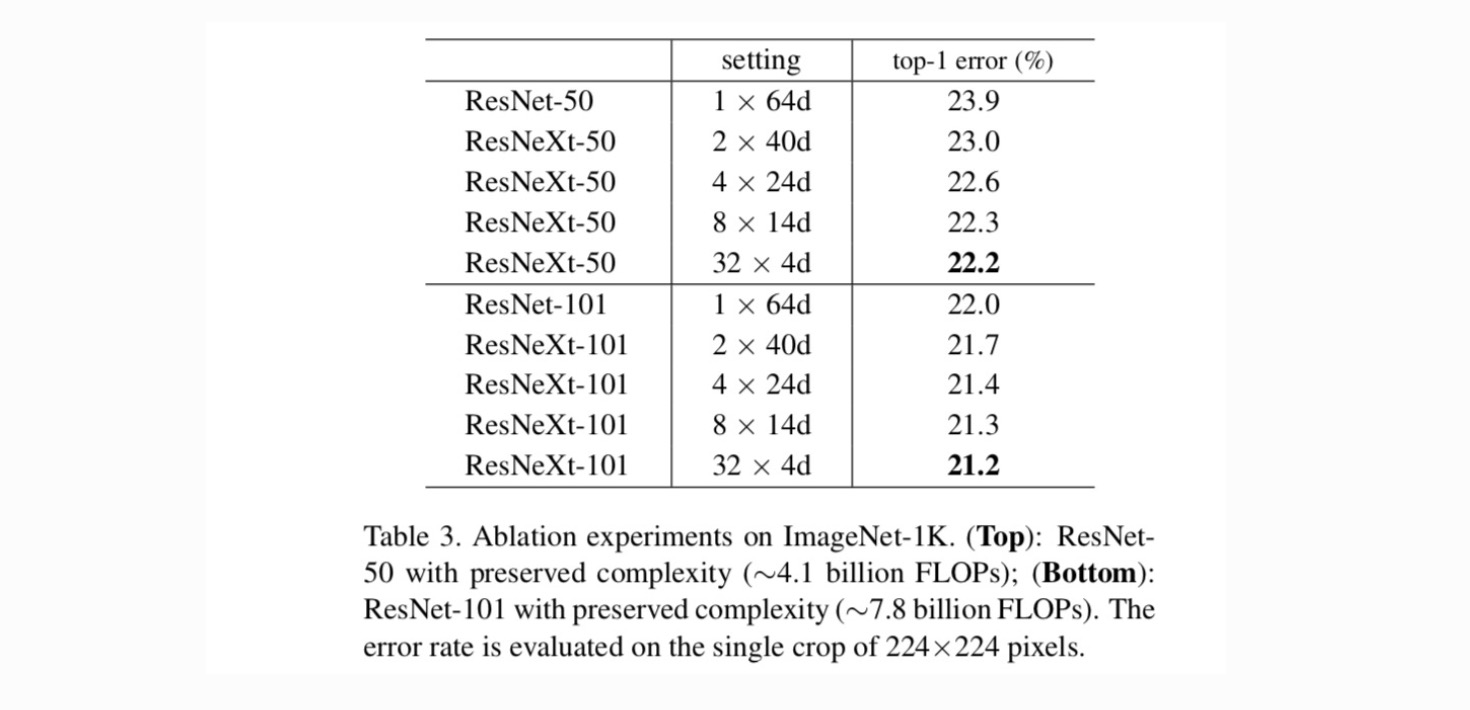
kasvava Kardinaalisuus vs. syvempi / laajempi.

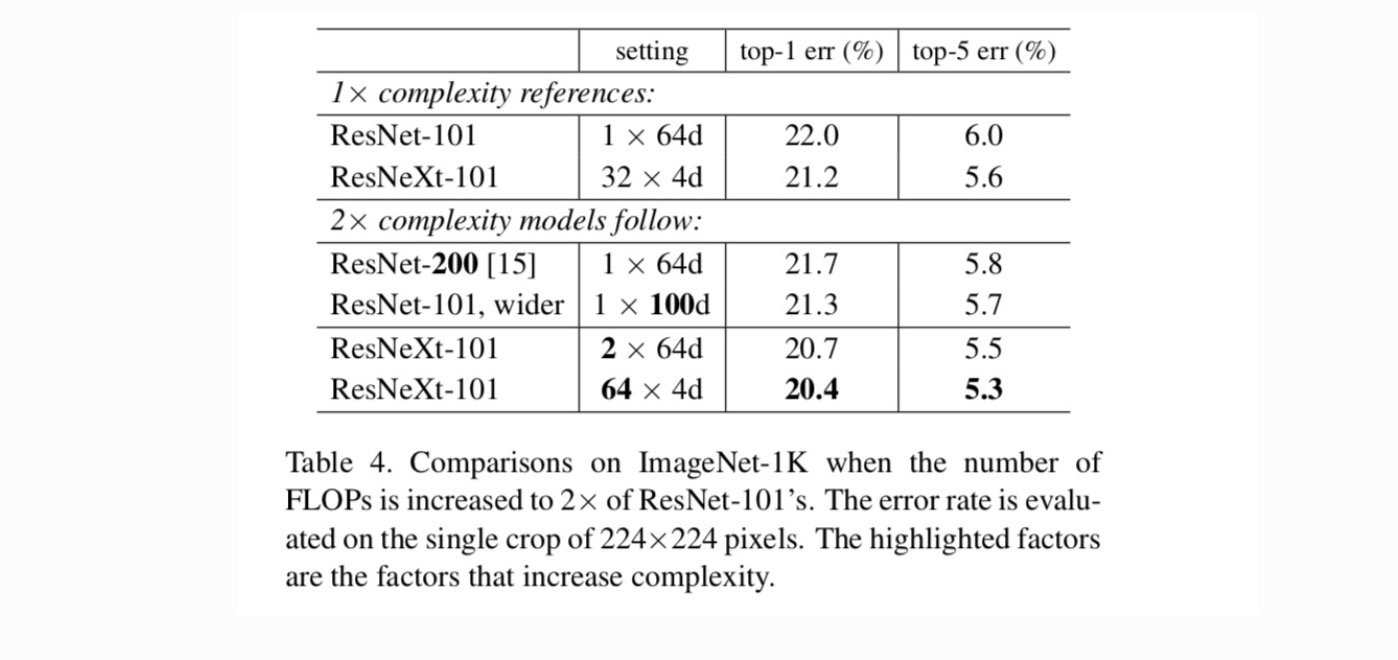
seuraavaksi tutkimme monimutkaisuuden lisääntymistä lisäämällä kardinaalisuutta C tai lisäämällä syvyyttä tai leveyttä. Vertaamme seuraavia variantteja (1), jotka ulottuvat syvemmälle 200 kerrokseen. Otamme käyttöön ResNet-200: n. (2) laajentamalla pullonkaulan leveyttä. (3) kardinaalisuuden lisääminen kaksinkertaistamalla C.

Taulukko 4 osoittaa, että monimutkaisuuden lisääminen 2× johdonmukaisesti vähentää virheitä verrattuna ResNet-101-lähtötilanteeseen (22, 0%). Mutta parannus on pieni, kun mennään syvemmälle (ResNet-200, 0,3%) tai laajempi (laajempi ResNet-101, 0,7%). Päinvastoin, kardinaalisuuden C lisääminen osoittaa paljon parempia tuloksia kuin syvemmälle tai laajemmalle meneminen.

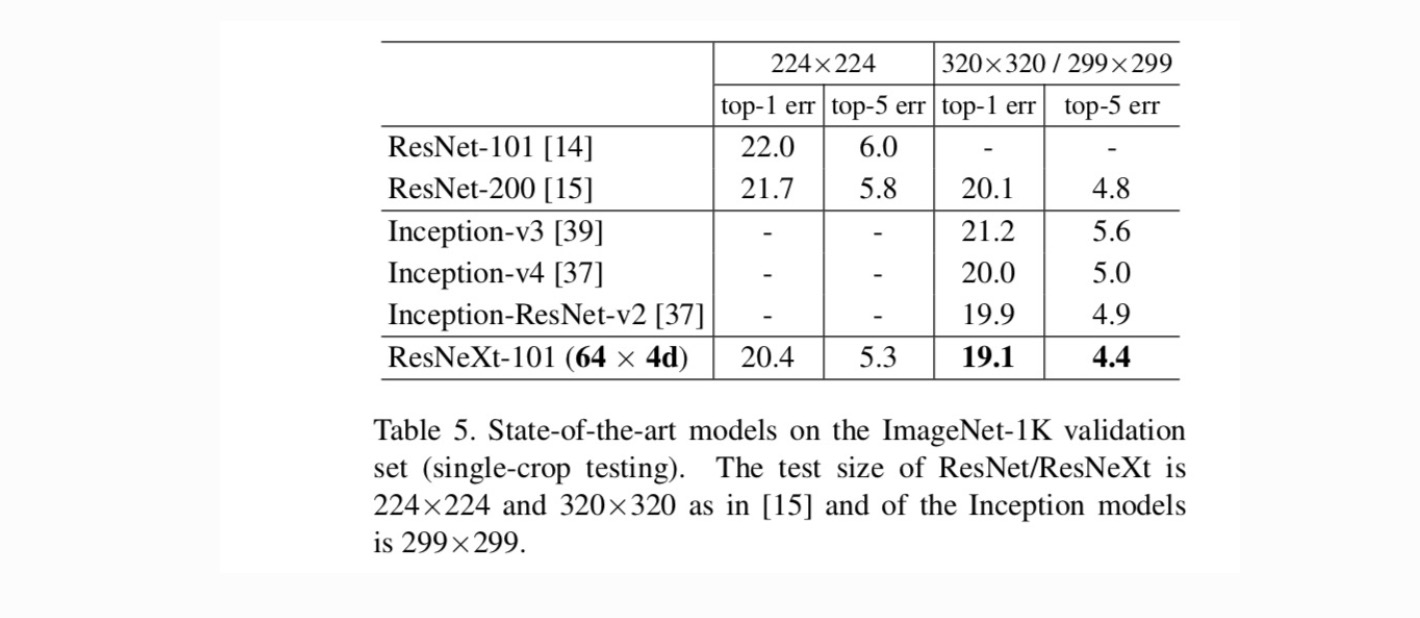
vertailut huipputuloksiin. Taulukossa 5 esitetään lisää yhden viljelykasvin testauksen tuloksia ImageNet-validointijoukossa. Tuloksemme vertautuvat suotuisasti ResNet, Inception-V3 / v4, ja Inception-ResNet-v2, saavuttaa yhden sadon top-5 virhetaso 4,4%. Lisäksi arkkitehtuurisuunnittelumme on paljon yksinkertaisempaa kuin kaikki Inception-mallit, ja vaatii huomattavasti vähemmän hyper-parametreja käsin määritettäväksi.