kone-ja syväoppimisessa malliparametrit ovat harjoitustietojen ominaisuuksia, jotka luokittaja tai muu ML-malli oppii koulutuksen aikana itsestään. Esimerkiksi painot ja harhat, tai jakopisteet Ratkaisupuussa.
mallin Hyperparametrit ovat sen sijaan ominaisuuksia, jotka ohjaavat koko harjoitusprosessia. Niitä ovat muuttujat, jotka määrittävät verkon rakenteen (esimerkiksi piilotettujen yksiköiden määrä) ja muuttujat, jotka määrittävät, miten verkkoa koulutetaan (esimerkiksi Oppimisnopeus). Mallin hyperparametrit asetetaan ennen harjoittelua (ennen painojen ja vinouden optimointia).
esimerkiksi tässä on joitakin mallin sisäisiä konfiguraatiomuuttujia:
- Oppimisnopeus
- aikakausien lukumäärä
- Piilokerrokset
- Aktivointifunktiot
Hyperparametrit ovat tärkeitä, koska ne ohjaavat suoraan harjoitusalgon käyttäytymistä, ja niillä on tärkeä vaikutus harjoiteltavan mallin suorituskykyyn.
sopivien hyperparametrien valinnalla on keskeinen rooli neuroverkkoarkkitehtuurien onnistumisessa, kun otetaan huomioon opittuun malliin kohdistuva vaikutus. Esimerkiksi jos oppimistahti on liian alhainen, malli jää kaipaamaan datan tärkeitä kuvioita; vastaavasti, jos se on korkea, siinä voi olla törmäyksiä.
hyvien hyperparametrien valinnalla on kaksi pääasiallista etua:
- Tehokas haku mahdollisten hyperparametrien väliltä; ja
- suuren hyperparametrien virityskokeiden hallinnan helpottaminen.
Hyperparametrit voidaan jakaa karkeasti kahteen kategoriaan:
1. Optimizer-hyperparametrit,
2. Mallikohtaiset hyperparametrit
ne liittyvät enemmän optimointiin ja harjoitteluun.
1, 1. Oppimisnopeus:
Jos mallioppimisnopeus on aivan liian pienempi kuin optimaaliset arvot, vie ideaalitilanteen saavuttaminen paljon pidemmän ajan (satoja tai tuhansia). Toisaalta, jos oppimistahti on paljon suurempi kuin optimaalinen arvo, niin se ylittäisi ideaalitilan ja algoritmi ei välttämättä lähentyisi. Kohtuullinen oppimisen aloitusprosentti = 0,001.
tärkeää ottaa huomioon, että:
a) mallilla on satoja ja tuhansia parametreja, joilla kullakin on oma virhekäyränsä. Ja oppimistahti joutuu paimentamaan niitä kaikkia
b) virhekäyrät eivät ole puhtaita u-muotoja, vaan niissä on yleensä monimutkaisempia muotoja paikallisilla minimeillä.
1, 2. Mini-Erän Koko:
eräkoko vaikuttaa harjoitusprosessin resurssivaatimuksiin, nopeuteen ja toistojen määrään ei-triviaalisti.
historiallisesti on käyty keskustelua stokastisen harjoittelun tekemisestä, jossa malliin sovitetaan yksi esimerkki datajoukosta ja suoritetaan vain yhtä esimerkkiä käyttäen eteenpäin syöttö, lasketaan virhe/backpropagate & asetetaan oikaistut arvot kaikille hyperparametreille. Ja sitten tehdä tämän uudelleen kunkin esimerkin dataset.
tai ehkä parempi syöttää koko data harjoitusvaiheeseen ja laskea gradientti sen virheen avulla, joka syntyy katsomalla kaikki aineistossa olevat esimerkit. Tätä kutsutaan eräkoulutukseksi.
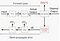
nykyään yleisesti käytetty tekniikka on asettaa minieräkoko. Stokastista harjoittelua on , kun minibatchin Koko =1, ja Eräharjoittelua, kun mini-erän koko = harjoitussarjan esimerkkien määrä. Suositeltavat lähtöarvot kokeille: 1, 2, 4, 8, 16, 32, 64, 128, 256.
suurempi minieräkoko mahdollistaa laskennalliset boostit, joissa harjoituslaskennassa hyödynnetään matriisilukujen kertolaskua . Se tulee kuitenkin sen kustannuksella, että harjoitusprosessiin tarvitaan lisää muistia. Pienempi minieräkoko aiheuttaa enemmän melua virhelaskelmissa, mikä on usein hyödyllisempää estää harjoitteluprosessia pysähtymästä paikallisiin minimeihin. Minieräkoon käypä arvo= 32.
niin, vaikka laskennallinen boost ajaa meitä kasvattamaan mini-erän kokoa, tämä käytännöllinen algoritminen hyöty kannustaa tekemään siitä pienemmän.
1, 3. Epookkien lukumäärä:
Jos haluat valita oikean määrän epookkeja harjoitusvaiheeseen, meidän tulisi kiinnittää huomiota Validointivirheeseen.
intuitiivinen manuaalinen tapa on saada mallijuna mahdollisimman monelle iteraatiolle niin kauan kuin validointivirhe vähenee jatkuvasti.
on olemassa tekniikka, jota voidaan käyttää nimellä Early Stopping päättämään, milloin mallin koulutus lopetetaan; kyse on koulutusprosessin lopettamisesta, jos validointivirhe ei ole parantunut viimeisten 10 tai 20 aikakauden aikana.
2. Mallin Hyperparametrit
ne ovat enemmän mukana mallin rakenteessa:
2.1. Piilotettujen yksiköiden lukumäärä:
piilotettujen yksiköiden lukumäärä on yksi salaperäisimmistä hyperparametreista. Muistakaamme, että neuroverkot ovat universaaleja funktion approksimaattoreita , ja jotta ne oppisivat approksimoimaan funktiota (tai ennustustehtävää), niillä täytyy olla tarpeeksi ”kapasiteettia”, jotta ne oppivat funktion. Piiloyksiköiden määrä on mallin oppimiskyvyn tärkein mittari.
yksinkertainen funktio saattaa tarvita vähemmän piilotettuja yksiköitä. Mitä monimutkaisempi toiminto, sitä enemmän malli tarvitsee oppimiskykyä.
hieman suurempi yksikkömäärä ei ole ongelma, mutta paljon suurempi määrä johtaa ylilataukseen (eli jos annat mallin, jolla on liikaa kapasiteettia, se saattaa olla taipuvainen ylilataukseen, yrittäen ”muistaa” aineiston, mikä vaikuttaa kykyyn yleistää)
2.2. Ensimmäinen piilotettu taso:
toinen heuristinen, johon liittyy ensimmäinen piilokerros, on se, että syötteiden määrää suurempien piiloyksiköiden asettaminen pyrkii empiirisen havainnon mukaan mahdollistamaan parempia tuloksia tehtävien määrässä.
2, 3. Kerrosten lukumäärä:
usein on niin, että 3-kerroksinen neuroverkko päihittää 2-kerroksisen. Mutta vieläkin syvemmälle meneminen harvoin auttaa paljon enemmän. (poikkeuksena ovat Convolutional Neuroverkkoja, jossa syvempi ne ovat, sitä paremmin ne suoriutuvat).
Hyperparametrien Optimointitekniikat
koneoppimisessa optimaalisimpien hyperparametrien löytöprosessia kutsutaan hyperparametrien optimoinniksi.
yleisiä algoritmeja ovat:
- Ruutuhaku
- Bayesilainen optimointi
Satunnaishaku
Ruutuhaku
Ruutuhaku on perinteinen tekniikka hyperparametrien toteuttamiseen. Kyse on jonkin verran raa ’ asta voimankäytöstä kaikissa yhdistelmissä. Grid search edellyttää kahden hyperparametrin luomista:
- Oppimisnopeus
- Kerrosten lukumäärä
Ruutuhaku kouluttaa algoritmin kaikille yhdistelmille käyttämällä kahta hyperparametrien joukkoa (Oppimisnopeus ja kerrosten lukumäärä) ja mittaa suoritusta ristivalidointitekniikalla. Tällä validointitekniikalla varmistetaan, että koulutettu malli saa suurimman osan datajoukon malleista (yksi parhaista validointimenetelmistä käyttämällä ”K-Fold Cross Validation” – menetelmää, joka auttaa tarjoamaan runsaasti tietoa mallin koulutusta varten ja runsaasti tietoja validointia varten).
Hilahakumenetelmä on yksinkertaisempi algoritmi käyttää, mutta se kärsii, jos datalla on suuriulotteinen avaruus, jota kutsutaan dimensionaalisuuden kiroukseksi.
Satunnaishaku
ottaa Hakuavaruuden satunnaisesti ja arvioi joukot määrätystä todennäköisyysjakaumasta. Sen sijaan, että yrittäisimme tarkistaa esimerkiksi kaikki 100 000 näytettä, voimme tarkistaa 1 000 satunnaisparametria.
satunnaishakualgoritmin käytön haittapuolena on kuitenkin se, että se ei käytä aiempien kokeiden tietoja seuraavan joukon valitsemiseen. Lisäksi kokeista on vaikea ennustaa seuraavaa.

bayesilainen optimointi
hyperparametriasetus maksimoi mallin suorituskyvyn validointijoukossa. ML-Algot vaativat usein mallin hyperparametrien hienosäätöä. Valitettavasti tätä viritystä kutsutaan usein ”mustaksi funktioksi”, koska sitä ei voida kirjoittaa kaavaan (funktion derivaatat ovat tuntemattomia).
houkuttelevampi tapa optimoida & hienosäätää hyperparametrit edellyttää automatisoidun mallivirityksen mahdollistamista-esimerkiksi Bayesilaisen optimoinnin avulla. Objektiivisen funktion approksimointiin käytettyä mallia kutsutaan sijamalliksi. Suosittu bayesilaisen optimoinnin sijamalli on Gaussin prosessi (GP). Bayesilainen optimointi toimii tyypillisesti olettamalla, että tuntematon funktio on otettu Gaussin prosessista (GP) ja ylläpitää posteriorijakaumaa tälle funktiolle sitä mukaa kuin havaintoja tehdään.
Bayesilaista optimointia suoritettaessa on kaksi päävalintaa:
- valitse ennen funktioita, jotka ilmaisevat oletuksia funktion optimoinnista. Tätä varten valitsemme Gaussin prosessin ennen;
- seuraavaksi on valittava hankintafunktio, jota käytetään utility-funktion rakentamiseen mallin posteriorista, jolloin voimme määrittää seuraavan arvioitavan pisteen.
Gaussin prosessi
Gaussin prosessi määrittelee edeltävän jakauman funktioille, jotka voidaan muuttaa posterioriseksi funktioiden suhteen, kun olemme nähneet jonkin verran dataa. Gaussin prosessi käyttää Kovarianssimatriisia varmistaakseen, että arvot ovat lähellä toisiaan. Kovarianssimatriisi sekä keskimääräinen µ-funktio, jolla saadaan odotusarvo hu (x), määrittää Gaussin prosessin.
1. Gaussin prosessia käytetään bayesilaisen päättelyn edeltäjänä;
2. Laskemalla posterioria voidaan tehdä ennusteita näkymättömistä testitapauksista.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Suositut hankintafunktiot ovat
- paranemisen Maksimitodennäköisyys (MPI)
- odotettu paraneminen (EI)
- Ylempi luottamusväli (UCB)
odotettu paraneminen (EI) on suosittu ja määritellään seuraavasti:
EI(x)=𝔼
missä L(x ) on nykyinen optimaalinen hyperparametrien joukko. Hyperparametrien maksimointi parantaa y-lukua.
