Johdatus liikkeen estimointiin optisen virtauksen kanssa

tässä opetusohjelmassa sukellamme optisen virtauksen perusteisiin, tarkastelemme joitakin sen sovelluksia ja toteutamme sen kaksi päävarianttia (harva ja tiheä). Keskustelemme lyhyesti myös uudemmista lähestymistavoista, joissa käytetään syväoppimista ja lupaavia tulevaisuuden suuntia.

Viimeaikaiset läpimurrot tietokonenäkötutkimuksessa ovat mahdollistaneet sen, että koneet pystyvät hahmottamaan ympäröivää maailmaa sellaisten tekniikoiden avulla kuin objektien havaitseminen tiettyyn luokkaan kuuluvien esineiden havaitsemiseksi ja semanttinen segmentointi pikseliviisaaseen luokitteluun.

reaaliaikaisen videotulon käsittelyssä useimmat näiden tekniikoiden toteutukset käsittelevät kuitenkin vain samassa kehyksessä olevien objektien suhteita \((x, y)\) ottamatta huomioon aikatietoa \((t)\). Toisin sanoen, he arvioivat jokaisen kehyksen uudelleen itsenäisesti, ikään kuin ne olisivat täysin toisiinsa liittymättömiä kuvia, jokaiselle ajolle. Entä jos tarvitsemme peräkkäisten kehysten välisiä suhteita, esimerkiksi haluamme seurata ajoneuvojen liikettä kehyksissä arvioidaksemme sen nykyisen nopeuden ja ennustaaksemme sen sijainnin seuraavassa kehyksessä?

tai vaihtoehtoisesti, mitä jos tarvitsemme tietoa ihmisen pose-suhteista peräkkäisten kehysten välillä tunnistaaksemme ihmisen teot, kuten jousiammunnan, baseballin ja koripallon?

tässä opetusohjelmassa opimme, mitä optinen virtaus on, kuinka toteuttaa sen kaksi päämuunnosta (harva ja tiheä), ja saamme myös ison kuvan uudemmista lähestymistavoista, jotka sisältävät syväoppimista ja lupaavia tulevaisuuden suuntia.

mikä on optinen virtaus?
harvan optisen virtauksen toteuttaminen
tiheän optisen virtauksen toteuttaminen
Syväoppiminen ja sen jälkeen

mikä on optinen virtaus?

aloittakaamme korkean tason ymmärryksellä optisesta virtauksesta. Optinen virtaus on kappaleiden liike peräkkäisten peräkkäisten kehysten välillä, mikä johtuu kohteen ja kameran välisestä suhteellisesta liikkeestä. Optisen virtauksen ongelma voidaan ilmaista seuraavasti:

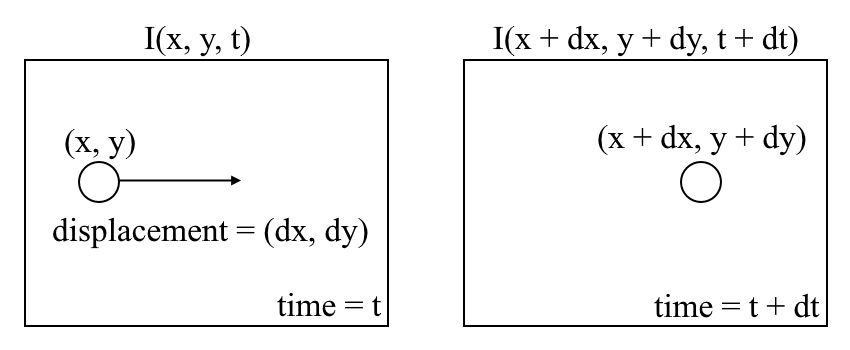
jossa peräkkäisten kehysten välillä voidaan ilmaista kuvan voimakkuus \((I)\) avaruuden funktiona \((x, y)\) ja aika \((t)\). Toisin sanoen, jos otamme ensimmäisen kuvan \(I (x, y, t)\) ja siirrämme sen pikseleitä \((DX, dy)\) \(t\) ajan kuluessa, saamme uuden kuvan \(I(x + dx, y + dy, t + dt)\).

ensinnäkin oletamme, että kohteen pikselitehot ovat vakio peräkkäisten kehysten välillä.

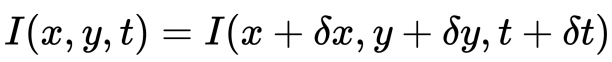
toiseksi otetaan RHS: n Taylorin sarjan likiarvo ja poistetaan yhteiset termit.

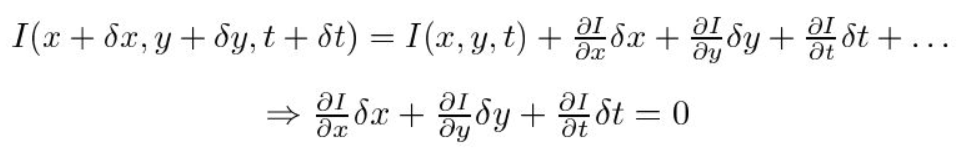
kolmas, jaamme \(dt\) johtaaksemme optisen virtauksen yhtälön:

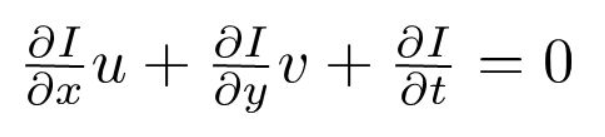
missä \(u = DX/dt\) ja \(v = dy / dt\).

\(dI/dx, dI/dy\) ja \(dI / DT\) ovat vaaka-akselin, pystyakselin ja ajan suuntaisia kuvagradientteja. Näin ollen päädymme optisen virtauksen ongelmaan, eli ratkaisemalla \(u (DX/dt)\) ja \(v (dy / DT)\) liikkeen määrittämiseksi ajan kuluessa. Saatat huomata, että emme voi suoraan ratkaista optinen virtaus yhtälö \(u\) ja \(v\), koska on olemassa vain yksi yhtälö kaksi tuntematonta muuttujaa. Otamme käyttöön joitakin menetelmiä, kuten Lucas-Kanade-menetelmän tämän ongelman ratkaisemiseksi.

harva vs tiheä optinen virtaus

harva optinen virtaus antaa virtavektoreille joitakin ”mielenkiintoisia ominaisuuksia” (sanotaan muutama pikseli kuvaa kohteen reunoja tai kulmia) kehyksessä samalla tiheän optisen virtauksen, jolloin saadaan koko kehyksen virtavektorit (kaikki pikselit) – jopa yksi virtavektori pikseliä kohti. Kuten olisit arvannut, tiheä optinen virtaus on suurempi tarkkuus kustannuksella on hidas / laskennallisesti kallista.

toteuttaessaan harvan optisen virtauksen

harvan optisen virtauksen valitsee harvan ominaisuusjoukon pikseleitä (esim.kiinnostavia ominaisuuksia kuten reunat ja kulmat) seuraamaan nopeusvektoreitaan (liikettä). Uutetut ominaisuudet kulkevat optisessa virtaustoiminnossa kehyksestä kehykseen, jotta samat kohdat saadaan seurattua. Harvan optisen virtauksen toteutuksia on useita, kuten Lucas–Kanade–menetelmä, Horn–Schunck-menetelmä, Buxton-Buxton-menetelmä ja paljon muuta. Toteutuksessa käytetään Lucas-Kanade-menetelmää OpenCV: n kanssa, joka on avoimen lähdekoodin kirjasto tietokonenäköalgoritmeista.

ympäristösi määrittäminen

Jos sinulla ei ole jo OpenCV: tä asennettuna, avaa pääte ja aja:

pip install opencv-python

nyt, kloonaa tutorial repository ajamalla:

git clone https://github.com/chuanenlin/optical-flow.git

Seuraava, avaa sparse-starter.py tekstieditorilla. Kirjoitamme kaikki tämän Python-tiedoston koodit.

määrittelemällä OpenCV: n lukemaan videota ja asettamalla parametreja

Shi-Tomasi Corner Detector – valitsemalla jäljitettävät Pikselit

harvan optisen virtauksen toteuttamiseksi, seuraamme vain kuvapisteiden ominaisuusjoukon liikettä. Kuvien ominaisuudet ovat kiinnostavia kohteita, jotka esittävät runsaasti kuvan sisältötietoa. Tällaisia ominaisuuksia voivat olla esimerkiksi kuvan kohdat, jotka ovat invariantteja kääntämisen, mittakaavan, pyörimisen ja intensiteetin muutosten kuten kulmien suhteen.

Shi-Tomasi-Kulmatunnistin on hyvin samankaltainen kuin suosittu Harris-Kulmatunnistin, joka voidaan toteuttaa seuraavilla kolmella menetelmällä:

1. määrittää ikkunat (pienet kuvapalikat) suurilla kaltevuuksilla (kuvan voimakkuuden vaihtelut) käännettynä sekä \(x\) että \(y\) suuntiin.
2. jokaisesta ikkunasta lasketaan pisteet \(r\).
3. \(r\) – arvosta riippuen jokainen ikkuna luokitellaan tasoksi, reunaksi tai kulmaksi.

Jos haluat tietää enemmän Harris Corner Detectorin vaiheittaisesta matemaattisesta selityksestä, voit vapaasti käydä nämä diat läpi.

Shi ja Tomasi tekivät myöhemmin pienen mutta tehokkaan modifikaation Harris Corner Detectoriin papereissaan hyvät ominaisuudet jäljitettäviksi.

muunnos on yhtälöön, jossa pisteet \(r\) lasketaan. Harris Corner Detectorissa pisteytysfunktio saadaan:

$$
\begin{array}{C}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} m=\lambda_{1} \lambda_{2}}\lambda_ {1}+\lambda_{2}}\end{array}
$$

sen sijaan shi-Tomasi ehdotti pisteytysfunktiota seuraavasti:

$$
r=\min\Left (\lambda_{1},\lambda_{2} \right)
$$

mikä periaatteessa tarkoittaa, että jos\(r\) on suurempi kuin kynnys, se luokitellaan kulmaksi. Seuraavassa verrataan Harrisin (vasemmalla) ja Shi-Tomasin (oikealla) pisteytysfunktioita \(λ1-λ2\) avaruudessa.

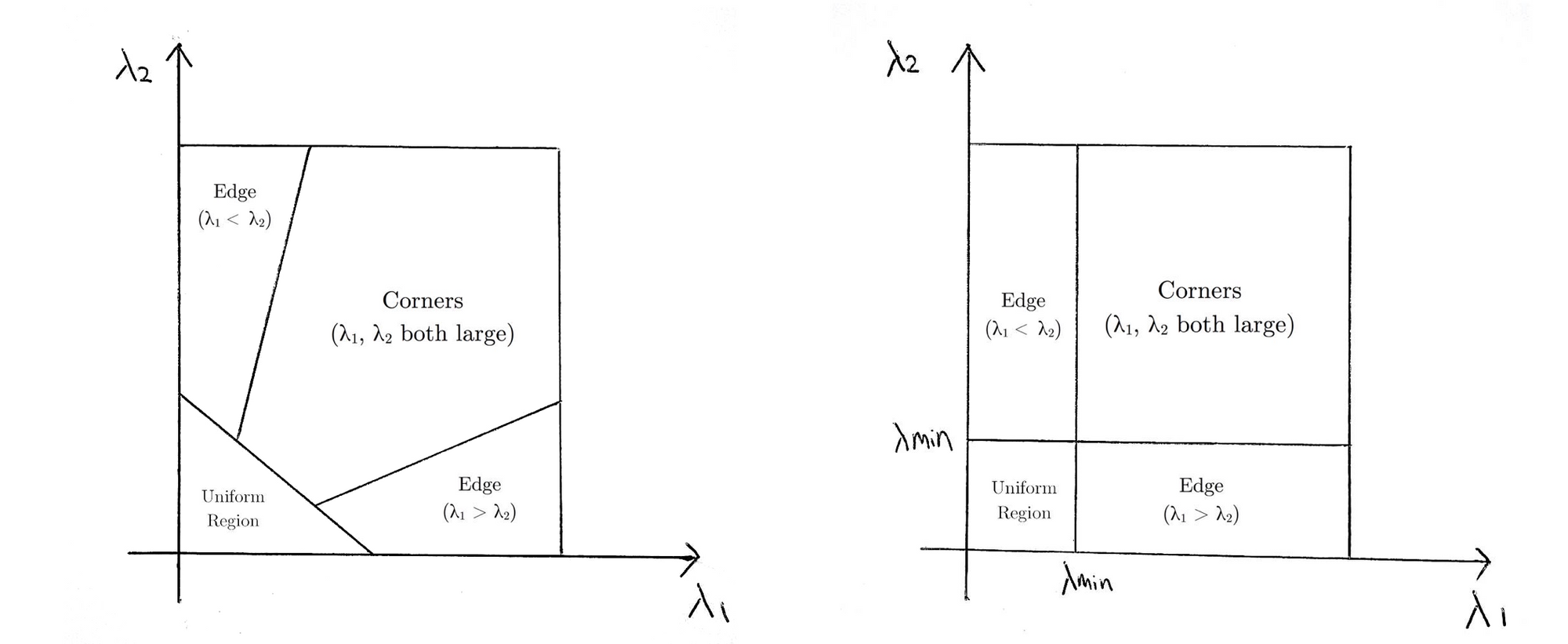
Shi-Tomasille vain silloin, kun \(λ1\) ja \(λ2\) ylittävät minimikynnyksen \(λmin\), ikkuna luokitellaan kulmaksi.

OpenCV: n dokumentaatio Shi-Tomasin toteuttamisesta goodFeaturesToTrack() löytyy täältä.

tiettyjen kohteiden jäljittäminen

voi olla tilanteita, joissa haluat seurata vain tiettyä kohdetta (sanotaan tietyn henkilön jäljittämistä) tai yhtä esineluokkaa (kuten kaikki 2 wheeler-ajoneuvoa liikenteessä). Koodin voi helposti muokata seuraamaan haluamiensa kohteiden pikseleitä muuttamalla prev muuttuja.

Voit myös yhdistää objektien havaitsemisen tähän menetelmään arvioidaksesi vain Havaittujen rajauslaatikoiden pikselivirran. Näin voit seurata kaikkia tietyn tyypin/luokan esineitä videolla.

Lucas-Kanade: harva optinen virtaus

Lucas ja Kanade ehdottivat tehokasta tekniikkaa mielenkiintoisten piirteiden liikkeen arvioimiseksi vertaamalla kahta peräkkäistä ruutua paperissaan Iteratiiviseen Kuvan Rekisteröintitekniikkaan Stereonäköön. Lucas-Kanade-menetelmä toimii seuraavilla oletuksilla:

1. kaksi peräkkäistä ruutua erotetaan toisistaan pienellä aikalisäyksellä (\(DT\)) siten, että objekteja ei siirretä merkittävästi (toisin sanoen menetelmä toimii parhaiten hitaasti liikkuvien kohteiden kanssa).
2. kehys kuvaa ”luonnollista” kohtausta, jossa on kuvioituja esineitä, joissa näkyy sulavasti vaihtuvia harmaan sävyjä.

ensinnäkin voidaan näiden oletusten perusteella ottaa pieni 3×3-ikkuna (naapurusto) Shi-Tomasin havaitsemien piirteiden ympärille ja olettaa, että kaikilla yhdeksällä pisteellä on sama liike.

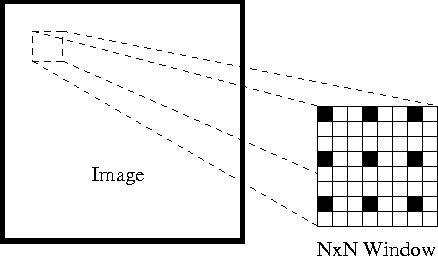
Tämä voidaan esittää muodossa

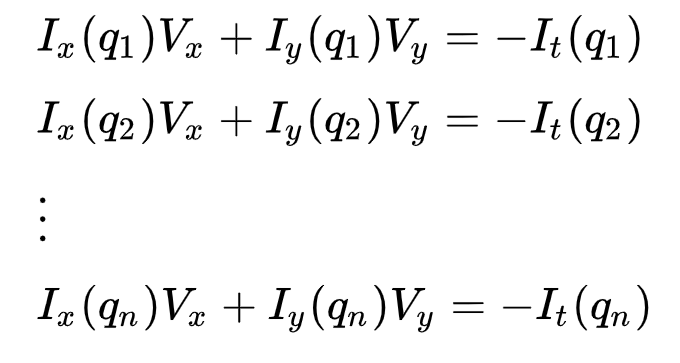
jossa \(q_1, q_2, …, q_n\) merkitsevät ikkunan sisällä olevia pikseleitä (esim. \(n\) = 9 3×3-ikkunassa) ja \(i_x(q_i)\), \(i_y(q_i)\) ja \(i_t(q_i)\) merkitsevät Kuvan \(I\) Osittaisderivaatat sijainnin \((x, y)\) suhteen ja aika \(t\), pikselille \(q_i\) tällä hetkellä.

Tämä on vain optinen Virtausyhtälö (jonka kuvasimme aiemmin) jokaiselle n-pikselille.

yhtälöiden joukko voidaan esittää seuraavassa matriisimuodossa, jossa \(Av = b\):

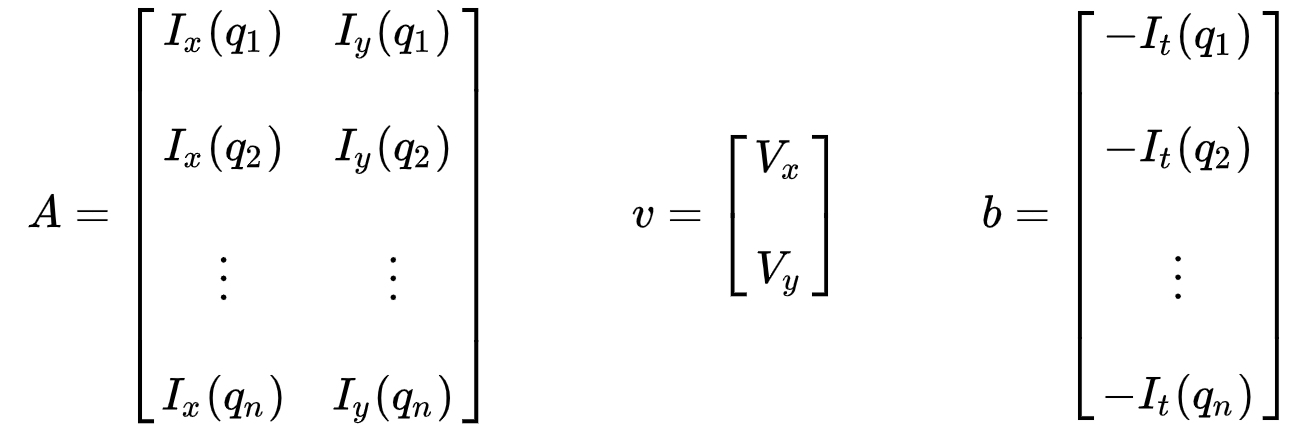
huomioi aiemmin (katso ”mikä on optinen virtaus?”jakso), jouduimme ratkaisemaan kaksi tuntematonta muuttujaa yhdellä yhtälöllä. Nyt edessä ottaa ratkaista kaksi tuntematonta (\(V_x\) ja \(V_y\)) yhdeksän yhtälöt, joka on ylimitoitettu.

toiseksi ylimitoitetun ongelman ratkaisemiseksi käytetään pienimmän neliösumman sopivuutta seuraavan kahden yhtälön-kahden-tuntemattoman ongelman saamiseksi:

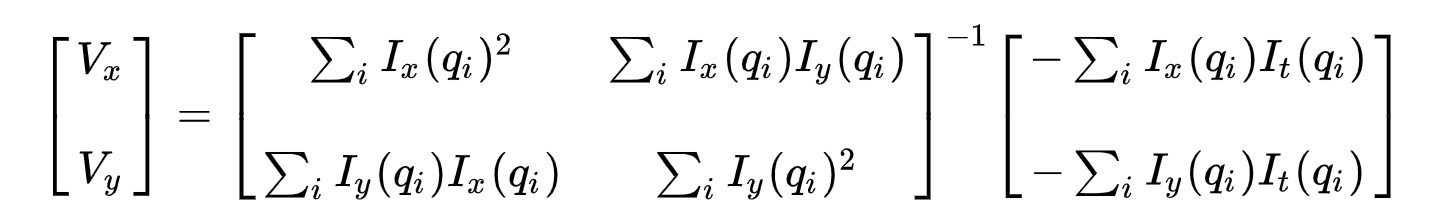
missä \(VX = U = DX/DT\) merkitsee \(X\) liikettä ajan kuluessa ja \(vy = v = dy/DT\) merkitsee Y: n liikettä ajan kuluessa. Kahden muuttujan ratkaiseminen täydentää optisen virtauksen ongelman.

pähkinänkuoressa tunnistamme joitakin mielenkiintoisia ominaisuuksia, joiden avulla voidaan seurata ja laskea iteratiivisesti näiden pisteiden optisia virtavektoreita. Lucas-Kanade-menetelmän omaksuminen toimii kuitenkin vain pienille liikkeille (alkuperäisestä oletuksestamme) ja epäonnistuu, kun on suuri liike. Siksi Lucas-Kanade-menetelmän OpenCV-toteutus omaksuu pyramidit.

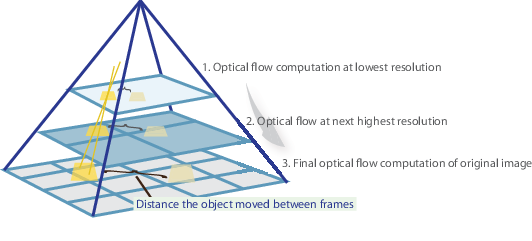
korkean tason näkymässä pienet liikkeet jäävät pyramidia ylös noustessa vähemmälle huomiolle ja suuret liikkeet pienenevät pieniksi liikkeiksi-laskemme optisen virtauksen yhdessä mittakaavan kanssa. Kattava matemaattinen selitys OpenCV: n toteutuksesta löytyy Bouguetin muistiinpanoista ja dokumentaatio OpenCV: n Lucas-Kanade-menetelmän toteuttamisesta calcOpticalFlowPyrLK() löytyy täältä.

visualisointi

ja se siitä! Avaa pääte ja aja

python sparse-starter.py

testaamaan harvan optisen virtauksen toteutusta. 👏

Jos jokin koodi on jäänyt huomaamatta, koko koodi löytyy sparse-solution.py.

toteutettaessa tiheää optista virtausta

olemme aiemmin laskeneet optisen virtauksen harvalle ominaisuusjoukolle pikseleitä. Tiheä optinen virtaus yrittää laskea optisen virtauksen vektoria jokaisen kehyksen jokaiselle pikselille. Vaikka tällainen laskenta voi olla hitaampaa, se antaa tarkemman tuloksen ja tiheämmän tuloksen, joka sopii sovelluksiin, kuten oppimisen rakenne liikkeestä ja videon segmentointi. Tiheän optisen virtauksen toteutuksia on erilaisia. Käytämme Farneback-menetelmää, joka on yksi suosituimmista toteutuksista, ja toteutuksessa käytetään OpenCV: tä, avoimen lähdekoodin tietokonenäköalgoritmikirjastoa.

ympäristösi määrittäminen

Jos et ole jo tehnyt niin, noudata vaihetta 1, jossa harvan optisen virtauksen käyttöönotto ympäristösi perustamiseksi tapahtuu.

seuraavaksi auki dense-starter.py tekstieditorilla. Kirjoitamme kaikki tämän Python-tiedoston koodit.

OpenCV: n määrittäminen lukemaan videota

Farneback Optical Flow

Gunnar Farneback ehdotti tehokasta tekniikkaa mielenkiintoisten ominaisuuksien liikkeen arvioimiseksi vertaamalla kahta peräkkäistä kehystä paperissaan kahden kehyksen liike-estimointi polynomin laajenemisen perusteella.

ensinnäkin menetelmä approksimoi kuvakehysten ikkunoita (Katso Lucas Kanaden jakso harvojen optisten virtausten toteutuksesta tarkempia tietoja) nelikulmaisten polynomien avulla polynomien laajennusmuunnoksen avulla. Toiseksi, tarkkailemalla, miten polynomi muuttuu käännöksessä (liikkeessä), määritellään menetelmä, jolla voidaan arvioida siirtymäkenttiä polynomin laajenemiskertoimista. Sarjan tarkennusten jälkeen lasketaan tiheä optinen virtaus. Farneback n paperi on melko tiivis ja suoraviivainen seurata, joten suosittelen käy läpi paperin, jos haluat enemmän ymmärrystä sen matemaattinen johtaminen.

OpenCV: n toteutuksessa se laskee optisen virtauksen suuruuden ja suunnan 2-kanavaisesta virtavektoriryhmästä \((DX/dt, dy / dt)\), optisen virtauksen ongelmasta. Sitten se visualisoi kulman (suunta) virtauksen hue ja etäisyys (suuruus) virtauksen arvo HSV väri esitys. HSV: n vahvuus on aina maksimissaan 255 optimaalisen näkyvyyden saavuttamiseksi. OpenCV: n dokumentaatio Farneback-menetelmän käyttöönotosta calcOpticalFlowFarneback() löytyy täältä.

visualisointi

ja se siitä! Avaa pääte ja aja

python dense-starter.py

testataksesi tiheän optisen virtauksen toteutusta. 👏

Jos jokin koodi on jäänyt huomaamatta, koko koodi löytyy dense-solution.py.

optinen virtaus käyttäen Syväoppimista

vaikka optisen virtauksen ongelma on historiallisesti ollut optimointiongelma, viimeaikaiset lähestymistavat syväoppimisen avulla ovat osoittaneet vaikuttavia tuloksia. Yleensä tällaiset lähestymistavat edellyttävät optisen virtauksen (värikoodattu kuva) ulostulona kahta videokuvaa, jotka voidaan ilmaista:

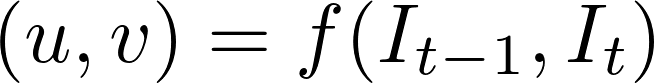
missä \(u\) on liike \(x\) suunnassa, \(v\) on liike \(y\) suunnassa ja \(f\) on neuroverkko, joka ottaa kaksi peräkkäistä kehystä \(i_{T-1}\) (frame at time = \(t-1)\) ja \(I_t\) (frame at time = \(t)\) syötteenä.

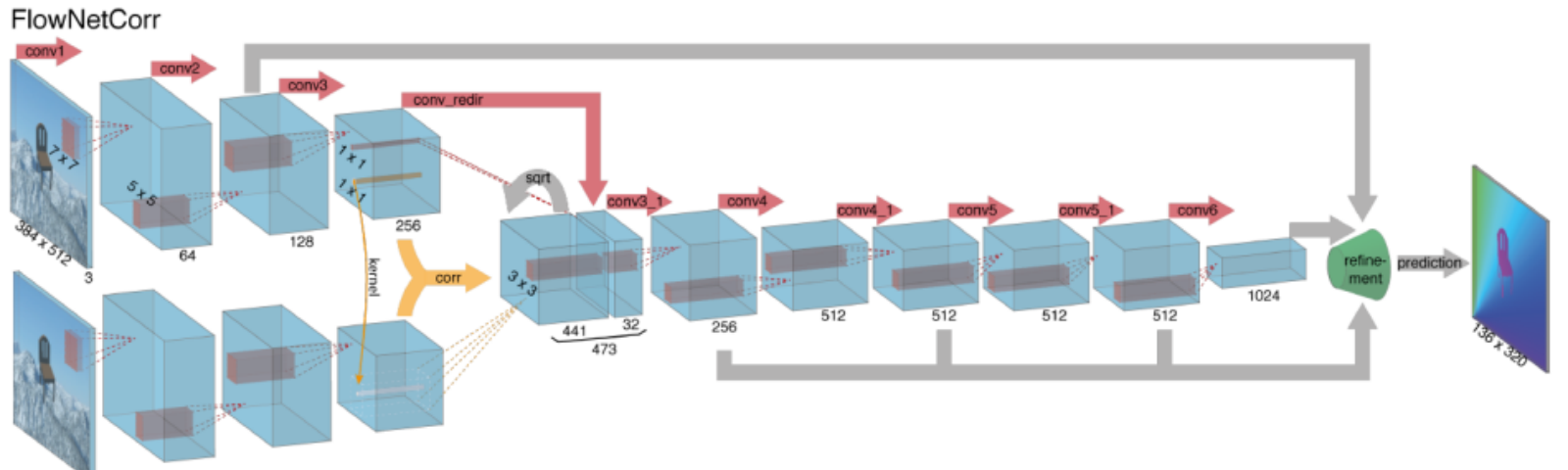
optisen virtauksen laskenta syvien neuroverkkojen avulla vaatii suuria määriä harjoitustietoa, jota on erityisen vaikea saada. Tämä johtuu siitä, että videomateriaalin merkitseminen optiseen virtaukseen vaatii kuvan jokaisen pisteen tarkan liikkeen tarkkaa selvittämistä subpixel-tarkkuudella. Käsitelläkseen koulutustietojen merkintää tutkijat käyttivät tietokonegrafiikkaa simuloidakseen massiivisia realistisia maailmoja. Koska maailmat syntyvät opetuksesta, tunnetaan jokaisen kuvan pisteen liike videosekvenssissä. Joitakin esimerkkejä tällaisista ovat mpi-Sintel, avoimen lähdekoodin CGI-elokuva, jossa Optiset virtausmerkinnät on tehty eri sekvensseille, ja Flying Chairs, monien tuolien datajoukko, joka lentää satunnaisten taustojen yli myös optisella virtausmerkinnällä.

optisten virtausongelmien ratkaiseminen syväoppimisen avulla on tällä hetkellä erittäin kuuma aihe, sillä Flownetin, Spynetin, PWC-Net: n ja muiden muunnokset päihittävät toisensa eri vertailuarvoilla.

optinen Virtaussovellus: semanttinen segmentointi

optinen virtauskenttä on valtava informaatiokaivos havaitulle kohtaukselle. Optisen virtauksen tarkkojen määritystekniikoiden parantuessa on mielenkiintoista nähdä optisen virtauksen sovelluksia Junctionissa useiden muiden perustavanlaatuisten tietokoneen visioiden kanssa. Esimerkiksi semanttisen segmentoinnin tehtävänä on jakaa kuva sarjoihin alueita, jotka vastaavat ainutlaatuisia objektiluokkia, mutta tiiviisti sijoitetut objektit, joilla on identtiset kuviot, ovat usein vaikeita yksittäisille kehyssegmentointitekniikoille. Jos kappaleet kuitenkin sijoitetaan erikseen, kohteiden erillisistä liikkeistä voi olla suurta hyötyä silloin, kun tiheän optisen virtauskentän epäjatkuvuus vastaa kappaleiden välisiä rajoja.

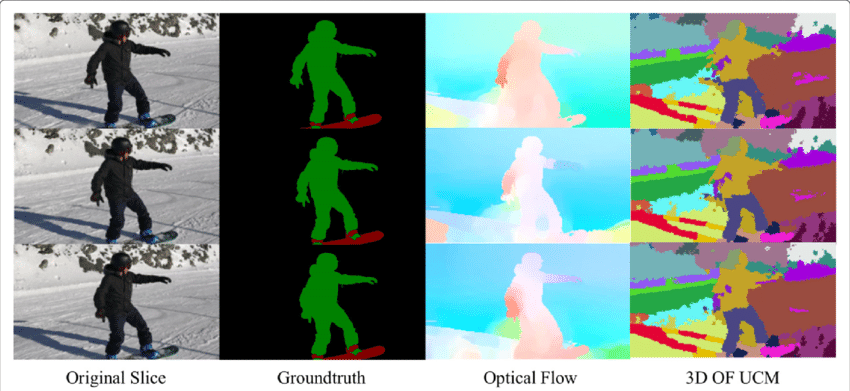
optinen Virtaussovellus: Object Detection & Tracking

toinen lupaava optisen virtauksen sovellus voi olla objektin havaitseminen ja seuranta tai korkean tason muodossa kohti reaaliaikaisten ajoneuvojen seuranta-ja liikenneanalyysijärjestelmien rakentamista. Koska harva optinen virtaus hyödyntää kiinnostavien kohteiden seurantaa, tällaiset reaaliaikaiset järjestelmät voidaan suorittaa ominaisuuteen perustuvilla optisilla virtaustekniikoilla joko kiinteästä kamerasta tai ajoneuvoihin kiinnitetyistä kameroista.

johtopäätös

pohjimmiltaan Optiset virtavektorit toimivat syötteenä lukemattomiin korkeamman tason tehtäviin, jotka vaativat videopätkien kohtausymmärrystä, kun taas nämä tehtävät voivat edelleen toimia rakennuspalikkina vielä monimutkaisemmille järjestelmille, kuten kasvojen ilmeiden analysoinnille, autonomiselle ajoneuvonavigoinnille ja paljon muulle. Optisen virtauksen uusia sovelluksia, joita ei ole vielä löydetty, rajoittaa vain sen suunnittelijoiden kekseliäisyys.

laiska koodaamaan, Etkö halua tuhlata GPU: Hon? Pään yli Nanonets ja rakentaa tietokoneen visio malleja ilmaiseksi!