mikä on ARIMAX-malli?

mikä on Arimax-malli?

Jos olet lukenut blogitutoriaalisarjamme aikasarjatietojen arviointimalleista, tunnet jo 3 suurta lähestymistapaa – autoregression, liukuvat keskiarvot ja integraation.

mikä on yhteinen teema kaikissa näissä malleissa?

he tukeutuivat ainoastaan yhteen muuttujaan.

mallissa voidaan kuitenkin ottaa huomioon muutakin kuin vain menneet hinnat tai menneet jäännökset.

ja nämä ovat niin sanottuja ”MAX”-malleja, joissa ARMAX on integroimaton versio ja ARIMAX-sen integroitu vastine.

tässä opetusohjelmassa aiomme tutkia, miltä ne näyttävät ja näyttää, miten ne toteutetaan Pythoniin vaihe vaiheelta.

Let ’ s get started, shall we?

miksi ARMAXIA ja ARIMAXIA kutsutaan ”MAX” – malleiksi?

nimet ARMAX ja ARIMAX tulevat Arman ja Ariman jatkeina. Loppuun lisätty X tarkoittaa ”eksogeenista”. Toisin sanoen, se ehdottaa lisäämällä erillinen eri ulkopuolella muuttuja auttaa mittaamaan endogeenisen muuttujan.

ARMAXIN ja ARIMAXIN mallin yhtälö:

koska ainoa ero ARMAXIN ja ARIMAXIN välillä on se, että toinen on integroitu ja toinen ei, voimme tutkia toista niistä ja sitten korostaa, miten toinen eroaisi.

tutkimme integroitua mallia viimeisessä blogiartikkelissamme (ARIMA), joten katsotaan, miltä arimaxin yhtälö näyttää.

ΔPt =C+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

tietysti armaksin yhtälö olisi sama, paitsi käyttäisimme varsinaista muuttujaa, vaikkapa P, sen Deltan sijasta.

Pt=C+ßX+ϕ1 Pt-1+ θ1 ϵt-1 +ϵt

hajottaen ARIMAX-yhtälön:

voimme ajatella ARMAXIA arimaxin erikoistapauksena, jossa integraation järjestys on 0.

niin, loput opetusohjelma, keskitymme ARIMAX.

ja aloitetaan purkamalla sen eri osat. Alkajaisiksi Pt ja Pt-1 edustavat arvoja kuluvalla kaudella ja 1 ajanjakso sitten vastaavasti.

vastaavasti ϵt ja ϵt-1 ovat virhetermejä samoille kahdelle jaksolle. Ja c on tietysti vain perusvakiotekijä.

kaksi parametria, ϕ1 ja θ1, ilmaisevat, mitkä arvon Pt-1 ja virhe ϵt-1 viimeisen jakson osat ovat merkityksellisiä arvioitaessa nykyistä.

nyt kaksi uutta lisäystä malliin ovat ”X” ja sen kerroin β. Aivan kuten ϕ, β On kerroin, joka arvioidaan mallivalinnan ja datan perusteella. Mutta entä X?

mikä on eksogeeninen muuttuja?

no, X on eksogeeninen muuttuja ja se voi olla mikä tahansa muuttuja, josta olemme kiinnostuneita.

se voi olla ajallisesti vaihteleva mitta, kuten inflaatiovauhti tai eri indeksin hinta. Tai kategorinen muuttuja, joka erottaa viikonpäivät toisistaan. Se voi olla myös Boolilainen tilitys erikoisista juhlakausista. Lopuksi se voi tarkoittaa useiden eri ulkoisten tekijöiden yhdistelmää.

ajatuksena on, että se voi olla mikä tahansa muu muuttuja tai muuttujat, jotka voivat vaikuttaa hintoihin, kunhan meillä on tieto käytettävissä.

tällaisia ulkopuolisia tekijöitä kutsutaan regressiossamme eksogeenisiksi muuttujiksi. Käytämme niiden arvoja ennustaa ja selittää yksi olemme kiinnostuneita, joka sattuu olemaan nykyiset hinnat meidän tapauksessa.

miten ARMAX-ja ARIMAX-mallit toteutetaan Pythonissa?

sopivasti statsmodels-pakettiin tulee Arima-niminen menetelmä, joka pystyy täysin käsittelemään tällaisia lisätuloja.

aluksi täsmennetään mallin ominaisuudet ja mallin järjestys:

sen jälkeen, kun olemme tehneet sen, on määriteltävä myös eksogeeniseksi argumentiksi kutsuttu ”eksog”.

arvon, jonka haluamme siirtää, on oltava jonkinlainen joukko, koska haluamme, että arvot liittyvät jokaiseen aikajaksoon.

esimerkiksi Voimme käyttää S&p hintoja tällä eksogeenisella muuttujalla, koska ne ovat jo meidän tiedoissamme.

nyt on valmiina Arimax (1,1,1) – malli.

muista nimetä mallimuuttujasi tavalla, joka erottaa sen vastaavista malleista. Tässä tapauksessa päätämme tehdä tämän lisäämällä” X, spx”loppuun osoittaaksemme, että eksogeeninen muuttuja on s&P.

sitten, kuten voidaan nähdä pätkiä, asetamme tämän yhtä suureksi kuin Arima-menetelmä kuten ennenkin, lisäämme aikasarjan ja järjestyksen, kuten olemme tottuneet. Lopuksi näiden kahden välille asetetaan ”eksog” – argumentti, joka on yhtä suuri kuin ”DF SPX”, joka ilmaisee s&p hinnat.

Jos sovit tähän malliin ja tulostat sen yhteenvetotaulukon, saamme lisärivin s&p hinnoille.

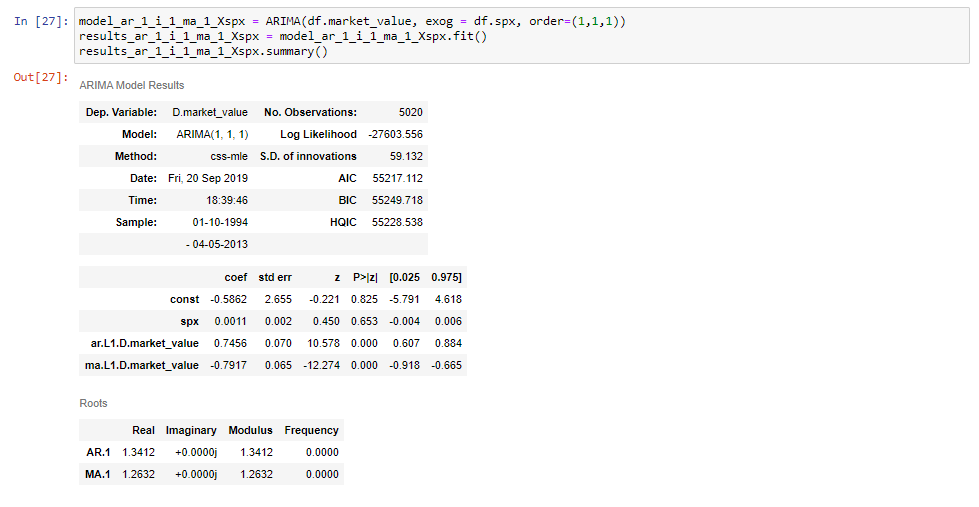
ja siinä kaikki!

olemme onnistuneesti nähneet, miten ARIMAX-malli toteutetaan Pythonissa.

Jos haluat oppia lisää Arimaxista ja muista Aikasarjamalleista Pythonissa, muista tarkistaa vaiheittaiset Python-tutoriaalimme. Jos olet uusi Python, ja olet innostunut oppimaan lisää, Tämä kattava artikkeli oppimisen Python ohjelmointi opastaa sinut koko matkan asennuksen kautta Python IDEs, Kirjastot, ja puitteet, paras Python urapolut ja työnäkymät.

valmis ottamaan seuraavan askeleen kohti datatieteen uraa?

Tsekkaa täydellinen Data Science-ohjelma tänään. Aloita perusteista tilasto -, Matikka-ja Excel-kursseillamme. Rakenna vaiheittainen kokemus SQL, Python, R, Power BI, ja Tableau. Ja päivitä taitosi koneoppimisen, syväoppimisen, Luottoriskimallinnuksen, aikasarja-analyysin ja asiakasanalytiikan avulla Pythonissa. Etkö vieläkään ole varma, että haluat kääntää kiinnostuksesi datatieteeseen uraksi? Voit tutustua opetussuunnitelmaan tai rekisteröityä 15 tunnin aloittelijan edistyneeseen videosisältöön ilmaiseksi klikkaamalla alla olevaa painiketta.