Unsupervised Bayesilainen päättely (reducing dimensions and unearthing features)
matalan tason ominaisuuksien havaitseminen edgejä käyttäen

lopuksi hetki, jota olette kaikki odottaneet, seuraava meidän valvomaton Bayesilainen päättelysarja: meidän (ei niin) syvä sukeltaa Sobel operaattori.
todella maaginen reunantunnistusalgoritmi, se mahdollistaa matalan tason piirteiden louhinnan ja dimensionaalisuuden vähentämisen, mikä olennaisesti vähentää kohinaa kuvassa. Se on ollut erityisen hyödyllinen kasvojentunnistussovelluksissa.
Irwin Sobelin ja Gary Feldmanin (Stanfordin Tekoälylaboratorio) vuoden 1968 rakkauslapsi, tämä algoritmi toimi inspiraationa monille moderneille reunantunnistustekniikoille. Kiertämällä kaksi vastakkaista ydintä tai naamiota tietyn kuvan päälle (esim. katso alla-vasen) (jokainen pystyy havaitsemaan joko vaaka-tai pystysuora reunat), voimme luoda vähemmän meluisa, tasoitetaan edustus (katso alla-oikea).
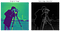
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel arvot (yleensä Luminanssi) erottamalla kunkin pikselin (ankkuripikseli) ja sitä ympäröivän pikselin välinen ero (lähinnä likimäärin kuvan derivaatta).
Tämä johtaa alkuperäisen kuvan tasoittumiseen ja pienemmän ulottuvuuden ulostuloon, jossa matalan tason geometriset piirteet näkyvät selvemmin. Näitä tuotoksia voidaan sitten käyttää tuloina monimutkaisempiin luokittelualgoritmeihin tai esimerkkeinä, joita käytetään valvomattomaan probabilistiseen klusterointiin Kullback-Leibler divergenssin (KLD) kautta (kuten nähdään viime blogissani LBP: ssä).
alemman ulottuvuuden ulostulon tuottaminen edellyttää, että otamme kuvan derivaatan. Ensin lasketaan derivaatta sekä x – että y-suuntiin. Luomme kaksi 3×3 ytimet (katso matriisit), jossa nollia pitkin keskellä vastaavan akselin, kaksi, keskellä neliöt kohtisuorassa Keski nolla ja ykköset kunkin kulmat. Kunkin nollasta poikkeavan arvon on oltava positiivinen nollien päällä/oikealla puolella (akselista riippuen) ja negatiivinen niiden vastaavalla puolella. Näiden ytimien nimet ovat Gx ja Gy.
nämä esiintyvät muodossa:
nämä ytimet kiertävät sitten kuvaamme sijoittaen kunkin ytimen keskipikselin kuvan jokaisen pikselin päälle. Laskemme matriisikertolaskun avulla uuden vastaavan pikselin intensiteettiarvon ulostulokuvassa jokaiselle ytimelle. Siksi päädymme kaksi lähtö kuvia (yksi kunkin karteesisen suuntaan).
tavoitteena on löytää ero / muutos kuvan pikselin ja kaikkien gradienttimatriisin (ytimen) pikselien (Gx ja Gy) välillä. Matemaattisesti tämä voidaan ilmaista muodossa.
sivuhuomautus:
me emme teknisesti konvolvoi mitään. Vaikka haluamme viitata’ convolutions ’ tekoäly-ja koneoppimisen piireissä, konvoluutio sisältäisi kääntää alkuperäisen kuvan. Matemaattisesti puhuen, kun viittaamme convolutions, olemme todella laskettaessa ristiin korrelaatio kunkin 3×3 alueen Tulo ja maskin kunkin pikselin. Lähtökuva on yleinen kovarianssi maskin ja syötön välillä. Näin reunat havaitaan.
Takaisin Sobelin selitykseemme…
lasketut arvot jokaiselle matriisikertolaskulle maskin ja tulon 3×3 osan välillä lasketaan yhteen, jotta saadaan lopullinen arvo kuvapisteelle lähtökuvassa. Tämä luo uuden kuvan, joka sisältää tietoa pysty-ja vaakasuuntaisten reunojen läsnäolosta alkuperäisessä kuvassa. Tämä on geometrinen ominaisuus esitys alkuperäisestä kuvasta. Lisäksi, koska tämä operaattori on taattu tuottamaan saman tuotoksen joka kerta, tämä tekniikka mahdollistaa vakaan reunan havaitseminen kuvan segmentointi tehtäviä.
näistä lähdöistä voidaan laskea sekä gradientin suuruus että gradientin suunta (käyttäen arctangentin operaattoria) millä tahansa pikselillä (x, y):
From näin voimme varmistaa,että ne pikselit, joilla on suuri magnitudi, ovat todennäköisemmin kuvan reuna, kun taas suunta ilmoittaa meille reunan suunnasta (vaikka suuntaa ei tarvita tuotoksemme tuottamiseen).
yksinkertainen toteutus:
tässä on yksinkertainen toteutus Sobel operaattori python (käyttäen NumPy) antaa sinulle tuntumaa prosessin (kaikille orastava koodarit siellä).
tämä toteutus on python-muunnelma Wikipedian pseudokoodiesimerkistä, jonka tarkoituksena on näyttää, miten tämän algoritmin voisi toteuttaa, mutta samalla havainnollistaa prosessin eri vaiheet.
miksi välitämme?
vaikka tämän operaattorin tuottama gradientin likiarvo on suhteellisen karkea, se tarjoaa äärimmäisen laskennallisesti tehokkaan menetelmän kuvien reunojen, Kulmien ja muiden geometristen ominaisuuksien laskemiseen. Se on puolestaan tasoittanut tietä useille dimensionaalisuuden vähentämiselle ja ominaisuuksien poistotekniikoille, kuten paikallisille Binäärikuvioille (katso lisätietoja tästä tekniikasta toisesta blogistani).
yksinomaan geometrisiin ominaisuuksiin nojaten on vaarana menettää tärkeitä tietoja datamme koodauksen aikana, mutta vaihtokauppa on se, mikä mahdollistaa datan nopean esikäsittelyn ja vuorostaan nopean koulutuksen. Siksi tämä tekniikka on erityisen hyödyllinen skenaarioissa, joissa tekstuuri ja geometriset ominaisuudet voidaan pitää erittäin tärkeinä syötteen määrittelyssä. Tämän vuoksi kasvojentunnistus voidaan suorittaa suhteellisen suurella tarkkuudella Sobel-operaattorin avulla. Tämä tekniikka ei kuitenkaan välttämättä ole paras valinta, jos yritetään luokitella tai ryhmitellä syötteitä, jotka käyttävät väriä pääasiallisena erottavana tekijänä.
tämä menetelmä on edelleen erittäin tehokas geometristen piirteiden pieniulotteisen esittämisen saavuttamisessa ja erinomaisessa lähtökohdassa dimensiollisuudelle ja kohinan vähentämiselle ennen muiden luokittelijoiden käyttöä tai käytettäväksi Bayesilaisissa päättelymenetelmissä.