the Mathematics of Surveying: Part II. The Planimetrer

Posted June 2008.

toinen kahdesta maanmittauksen matematiikkaa käsittelevästä sarakkeesta (ensimmäinen on tässä). …

Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca

John Eggers
University of California, San Diego
jeggers at ucsd.edu

Mail to a friend

print this article

planimetri on pöytäväline, jolla mitataan alueita, yleensä epäsäännöllisten alueiden alueita kartalla tai valokuvassa. Ne olivat aikoinaan yleisiä, mutta nykyään ne on suurelta osin korvattu digitaalisilla työkaluilla.

seuraava kuva antaa jonkinlaisen käsityksen asetelmasta. Pylväsvarsi pyörii vapaasti navan ympäri, joka on kiinnitetty pöydälle. Merkkivarsi pyörii Pivotin ympäri, jolloin se yhtyy napavarteen. Voit jäljittää käyrän myötäpäivään merkkiaineen kanssa, ja kun teet niin, mittauspyörä rullaa eteenpäin, ja kokonaisetäisyys, jonka se rullaa, kertyy kellotauluun. Tukipyörä estää laitteen floppaamisen. Lopussa luetaan kellotaulusta luku pois, ja kun kertolasku tehdään vain planimetrin tietyn konfiguraation mukaan, saadaan käyrän sisällä oleva pinta-ala.

seuraava luku antaa paremman kuvan mekanismista.

kutsumme vaunua pyörien, kellotaulun ja Pivotin kokoonpanoksi. Seuraavassa kuvassa näet sen tarkemmin ja näet matoajon, joka saa kellotaulun pyörimään mittauspyörän liikkuessa.

tässä on alkuperäisen planimetrin kaavio Jakob Amslerin artikkelista, joka esitteli sen:

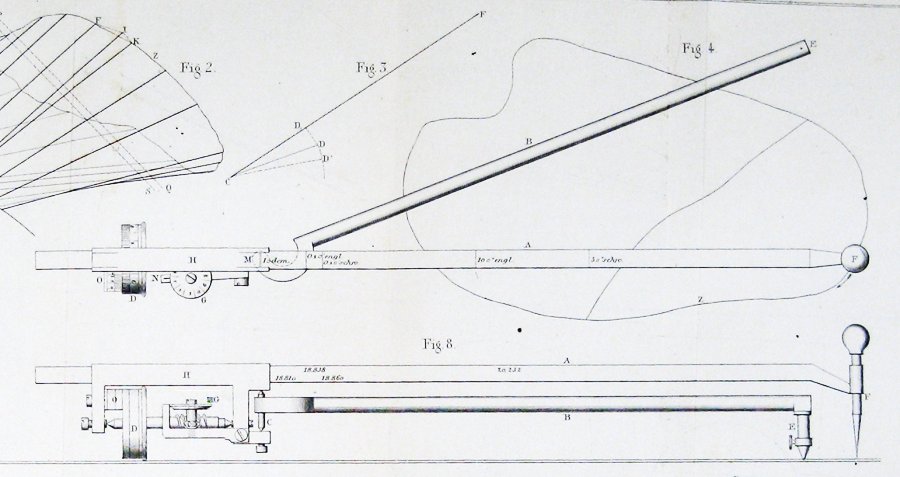
miten tällainen yksinkertainen asia voi mitata alueita?

planimetrin geometria

planimetrin myötäpäiväinen liike on suunta, joka on päinvastainen kuin mitä matemaatikot ovat päättäneet olevan positiivinen kierto. Sen sijaan rikkoa tätä yleissopimusta, aiomme työskennellä nyt kanssa matemaatikon planimetri, jossa voit liikkua vastapäivään. Kuten muiden matemaatikkojen fantasioita, niitä ei ole tällä planeetalla!

on joitakin rajoituksia, miten planimetri sijoitetaan sen käyrän suhteen, jonka haluat jäljittää. Vaunua voidaan liukua merkkivartta pitkin, mutta kaikissa tapauksissa merkkivarren pituus l on pienempi kuin pylväsvarren pituus r. Tämä tarkoittaa, että merkkiaine ei voi koskaan päästä etäisyydelle R-l navasta. Toisaalta, kun se on täysin laajennettu, merkkiaine voi koskaan päästä yli r + l. joten käyrä voidaan jäljittää on sijaittava renkaan välillä kaksi ympyrää, joista toinen on säde r-l, toinen r + l.

itse asiassa hetken kuluttua pitäisi tulla selväksi, ettei käsivarsia saa koskaan kokonaan ojentaa, joten jäljitettävän käyrän täytyy sijaita kokonaan renkaan sisällä. Lisäksi tolppa sijoitetaan normaalisti kaarteen ulkopuolelle.

tietylle renkaan pisteelle on täsmälleen kaksi mahdollista planimetrin konfiguraatiota, jotka asettavat merkkiaineen kyseiseen pisteeseen. Yhden pisteen tai toisen valitseminen tarkoittaa merkin valitsemista neliöjuurelle. Kutsumme tätä suuntauksen valitsemiseksi planimetrille. Se on positiivinen, jos neliöjuuri on positiivinen. Kun suunta on valittu, se pysyy samana, ellei käsivarsi ole täysin ojennettu. Näin ei saa koskaan tapahtua. Niin kauan kuin käyrä on täysin renkaan sisällä, planimetrin kokoonpanot vaihtelevat tasaisesti ja yksilöllisesti merkkiaineen reitin mukaan.

seuraavaksi pitää ymmärtää muutama asia mittapyörän liikkeestä. Kuten seuraava kuva osoittaa, jos pyörä kulkee suoralla linjalla matkan C, pyörä pyörii kulman θ = C / R kautta, jossa R on sen säde.

on siis todella totta, että pyörän pyörimisellä ja merkkivarren kulkemalla matkalla on jonkinlainen yhteys toisiinsa. Mutta tämä suhde on hieman hienovarainen. Jos käsivarsi vain liikkuu suoraan eteenpäin etäisyys C, pyyhkäisty alue on lC, mutta jos se siirtyy samansuuntaisesti itsensä pyyhkäisty alue on 0. Ensimmäisessä tapauksessa pyörän kehällä oleva piste siirtää etäisyyttä C. toisessa tapauksessa pyörä ei liiku lainkaan. Ja jos varsi kääntää vinosti, pyörä kiertää matkan, joka vastaa varren kattaman suuntaissärmän korkeutta. Kaikissa tapauksissa, joissa varsi kääntyy samansuuntaisesti itsensä kanssa, merkkivarren Pivotin ja merkkiaineen välisen osan pyyhkimä alue on yhtä suuri kuin lC, jossa C on pyörän pyörimisellä mitattu etäisyys. Tämä on olennainen seikka, joka liittyy varren liikkeeseen mittauspyörän liikkeeseen.

tapa lausua tämä tarkasti on, että riippumatta siitä, miten varsi liikkuu, pyörän mittaama matka on polkuintegraali

missä Γ on varren pisteen kulkema polku, johon mittauspyörä on kiinnitetty, n on yksikkövektori kohtisuorassa arm milloin tahansa, ja t on kulkusuuntaan osoittava yksikkövektori (siten, että esimerkiksi jos varsi liikkuu itsensä suuntaisesti, N: n ja T: n pistetulo on 0).

Guldinin lause

seuraavaksi yritämme tehdä planimetrin käyttäytymisestä intuitiivisesti selvää, mutta ensin tarkastelemme erityistä planimetrin muotoa ja tässä tapauksessa todistamme yleisemmän tuloksen. Oletetaan, että otamme yhden vapaasti liikkuvan varren pituuden l ja kiinnitämme siihen mittauspyörän, jonka säde on R, aivan sen keskelle.

tämän jälkeen liikutellaan käsivartta tasossa. Jos mittapyörä pyörii kokonaiskulman θ radiaaneina varren liikkuessa ympäri, etäisyys kehällä oleva piste kulkee on C = θR.

Guldinin lause. Tässä tilanteessa käsivarren pyyhkimä kokonaispinta-ala on tuote lC.

alue tulkitaan tässä merkillä. Jos varsi vain pyörii keskipisteensä ympäri, toinen puoli käsivarresta menee eteenpäin ja toinen taaksepäin, ja kaksi peruuttaa.

olemme jo nähneet, että Guldinin väite on pätevä siinä tapauksessa, että käsi vain kääntää. Aina näin ei tietenkään käy – käsi saattaa pyörähtää liikkuessaan sekä kääntää. Mutta voimme nähdä, mitä tapahtuu pilkkomalla pyyhkäisty alue seuraavasti:

koska mittapyörä on varren keskellä, varren pyöriessä se litistää pieniä palikoita toiselta puolelta laajentaessaan niitä toiselta puolelta. Nämä vaikutukset kumoavat toisensa täsmälleen.

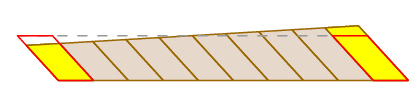
täysin tiukka todistus voidaan antaa käyttämällä muuttujien muuttumisen kaavaa kaksoisintegraalissa ja pyörän kulkemisen lauseketta polkuintegraalina.

nyt oletetaan, että pyörä on sijoitettu jonnekin muualle. Sano, että sen sijainti on c + v, jossa C on varren keskipiste ja v vektori käsivartta pitkin. V: n pituus pysyy kiinteänä, vaikkapa ρ: ssä. Polku, jota pyörä seuraa, on c(t) + v (t). Polkuintegraali on nyt

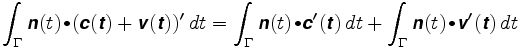
ensimmäinen integraali on matka, jonka pyörä kulkisi, jos se olisi varren keskellä. Toisessa vektori v (t) on aina kohtisuorassa n: n kanssa, ja v(t): n pituus on vakio. Vektori v (t) liikkuu ympyrällä, jonka säde on ρ. Näin ollen n: n ja v'(t): n pistetulo on vain v'(t): n allekirjoitettu pituus, ja toinen integraali on yhtä suuri kuin ρ kertaa varren kokonaiskierto. Siten:

Jos pyörä on etäisyydellä ρ varren keskipisteestä, pyörän mittaama etäisyys C on C0 , etäisyys, joka mitattaisiin, jos pyörä olisi keskipisteessä, plus ρ kertaa kokonaiskulma θ, jota varsi kiertää.

tästä näkee heti yhden yksinkertaisen tapauksen kiertämällä käsivartta sen keskustan ympäri. Yhdistämällä tämä guldinin lause, näemme, että kaikissa tapauksissa:

c = C0 + ρ θ
pinta – ala pyyhkäisty pois = l C0 = l c – l ρ θ

koko tulos

Guldinin kaava antaa allekirjoitetun alueen-jos pyyhkäisee takaperin jonkin alueen yli, pyörä menee taaksepäin ja peruutetaan alue, jonka on jo kattanut. Jos sovellamme tätä tapauksessa, jossa vapaa arm tulee takaisin täsmälleen missä se alkoi, näemme, että lC on yhtä suuri kuin suljetun alueen jäljitetty oikealla puolella arm miinus että alueen pyyhkäisi ulos vasemmalla.

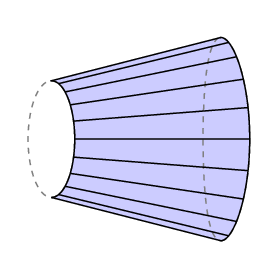
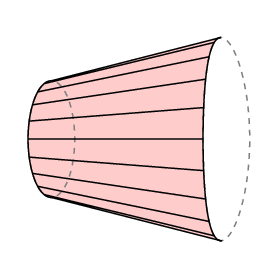
polaariplanimetrin tapauksessa varren alaosa rajoittuu kaareen, jonka säde on R ja jonka napa on keskellä, joten l C on alue, jota jäljitin jäljitti. Lisäksi yleensä napa on mitattavan alueen ulkopuolella, ja tällöin varren kiertymisen kokonaismäärän on oltava 0. Joten tässä tapauksessa meillä on

alueen alue traced = LC

tässä on luku, jonka keksijä Jakob Amsler sisällytti alkuperäiseen tutkielmaansa keksimästään instrumentista:

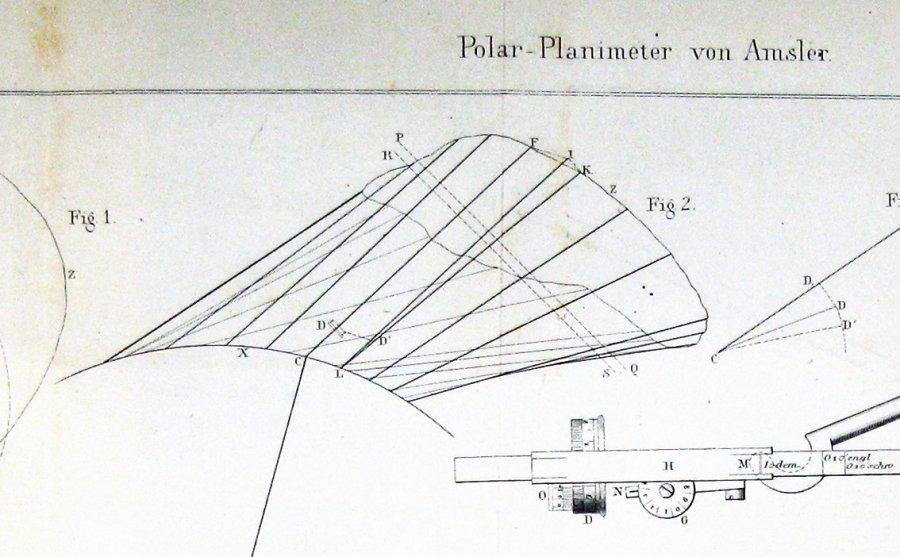
näyttää melko selvältä tästä, että Amsler johdatti konstruktionsa jonkinlaisen guldinin lauseen kautta.

Planimetrit ja Greenin lause

kuten olemme jo maininneet, kun olemme valinneet planimetrin suunnan, planimetrin konfiguraatio on merkkiasennon jatkuva funktio. Sanotaan, että valitsemme positiivisen suunnan. Sitten voimme liittää kunkin pisteen, renkaan yksikkö vektori n, joka osoittaa vastapäivään ja kohtisuorassa merkkiaineen arm on merkkiaine.

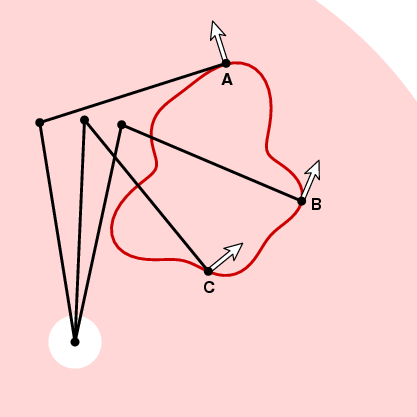
se, miten mittapyörä reagoi seuraavassa hetkessä käyrän suuntaiseen liikkeeseen, riippuu tämän vektorin ja käyrän yksikkötangenttivektorin välisestä kulmasta. Yllä olevan kuvan A kohdalla mittauspyörä ei liiku, koska liike käyrää pitkin on samansuuntainen merkkivarren kanssa. B: ssä jos merkkiaine liikkuu pienen matkan ds: n, niin myös mittauspyörä. Ja C: ssä mittauspyörä liikkuu jonkin matkaa välillä 0 ja ds. Jos ollaan tarkkoja, oletetaan, että t on yksikön tangenttivektori jossakin käyrän kohdassa. Jos merkkiaine liikuttaa etäisyyttä ds pitkin käyrää, siinä pisteessä mittauspyörä liikuttaa etäisyyttä d ds, jossa D = n . t, yksikkövektorien t ja n pistetulo. toisin sanoen, jos liikumme kaikki käyrän Γ ympäri, mittauspyörä liikkuu kokonaisetäisyydellä, joka on yhtä suuri kuin n: n integraali . t ds (pistetulo), tai

, mutta koska jokainen renkaan piste vastaa planimetrin ainutlaatuista positiivista konfiguraatiota, voimme määrittää vektorin n jokaiselle renkaan sisäpisteelle, ja siten se määrittelee vektorikentän. Käyrä Γ on sen sisäosan Ω raja, ja erään oletuksemme mukaan tämä sisältyy kokonaan alueelle, jossa n on määritelty. Greenin lause kertoo, että polkuintegraali tämän alueen rajan ympärillä on yhtä suuri kuin tietty integraali Ω: n yli: Siksi

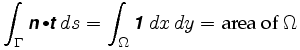
tarkemmin Greenin lause kertoo, että

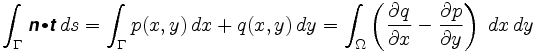
missä n = on mukana oleva vektorikenttä. Kaksoisintegraalin integraalia kutsutaan vektorikentän kiharaksi.

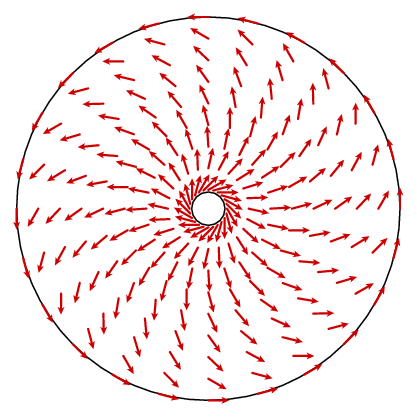
tällä ei näytä pääsevän kovin pitkälle. Mitä pitäisi tapahtua on, että curl on vakio 1. Periaatteessa voisimme löytää kaavan vektorikentälle n ja laskea sen kaaren, mutta se ei ole kovin valaisevaa. Voimme kuitenkin hyödyntää toista seikkaa. Vektorikentällä on ympyräsymmetria, eli se määräytyy sen mukaan, mikä se on yhdellä säteellä. Kosinilaki antaa yksinkertaisen kaavan kehäosalle.

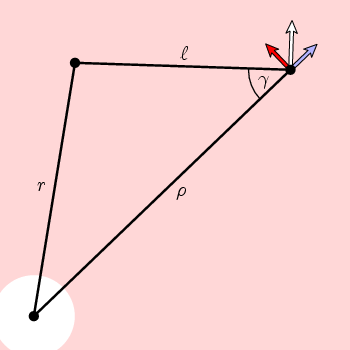
tämän luvun yksinkertaisesta geometriasta seuraa, että n: N kehäkomponentti on

f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)

Greenin lauseen todellinen piste on, että integrandin arvon 1 todentamiseksi riittää, että polkuintegraali kiertää sopivia pieniä polkuja on sama kuin alue. Tätä varten valitsemme alueemme sellaisiksi kuin täällä:

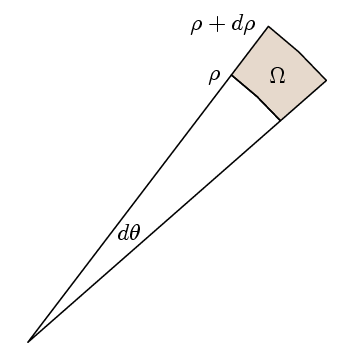
silloin l kertaa polkuintegraali on

l (ρ+DP)( f(ρ+DP)- f(ρ) ) dθ

tai

(θ/2) ( (ρ + dp) 2 – ρ 2)

, joka on Alueen Ω pinta-ala.

muunlaiset planimetrit

Guldinin lause tarkoittaa, että mittapyörän liike kertoo merkkiaineen jäljittämän alueen aina, kun varsi, jossa on mittapyörä, jäljittää käyrän, mutta sen toinen pää rajoittuu yksiulotteiseen käyrään. Näin tapahtuu esimerkiksi vierintäplanimetrin kanssa, jossa nivel on rajattu suoraksi olemalla valssisylinterin päällä.

lisätietoja

• valmistaa ja myy edelleen planimetrejä.
• differentiaali-ja integraalilaskennan osa II, R. Courant, Blackie & Son, 1936. Guldinin kaavaa käsittelevä osio (s. 294-298) tarjoaa selityksen siitä, miten planimetri toimii.
• Amslerin alkuperäinen artikkeli, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Tästä puuttuvat kaaviot, mutta ne ovat tässä:
  • Amslerin ensimmäinen kaavio
  • Amslerin toinen kaavio

  kiitos Donna Sammis Stony Brookin yliopiston kirjastosta artikkelin paikantamisesta ja hänen miehelleen Robertille kuvien toimittamisesta.

  amslerin perustama yhtiö valmisti soittimia pitkälle 1900-luvulle. Kuvassa on planimetrin virroitinversiossa oleva logo:

  

• ”Planimetreistä”, Konetarjonta. Yhtiö on julkaissut videon myös YouTubessa.

Bill Casselman
University of British Columbia, Vancouver, Kanada
cass at math.ubc.ca

John Eggers
University of California, San Diego
jeggers at ucsd.edu

ne, jotka pääsevät jstoriin, voivat löytää sieltä joitakin edellä mainittuja papereita. Niille, joilla on pääsy, American Mathematical Society ’ s MathSciNet voidaan saada lisää bibliografista tietoa ja arvioita joistakin näistä materiaaleista. Joihinkin yllä oleviin kohteisiin pääsee käsiksi ACM-portaalin kautta , joka tarjoaa myös bibliografisia palveluja.