Introduction
Principal Components Analysis (PCA) on dimensionality reduction algorithm, jota voidaan käyttää merkittävästi nopeuttamaan unspervised feature learning algoritmia. Vielä tärkeämpää on, että PCA: n ymmärtäminen auttaa meitä myöhemmin toteuttamaan valkaisun, joka on tärkeä esikäsittelyvaihe monille algoritmeille.
Oletetaan, että koulutat algoritmiasi kuvien perusteella. Silloin tulo on jokseenkin tarpeeton, koska vierekkäisten pikselien arvot kuvassa korreloivat suuresti. Oletetaan, että harjoittelemme 16×16: lla harmaasävykuvamerkillä. Sitten \textstyle x\in \Re^{256} ovat 256-ulotteisia vektoreita, joissa yksi ominaisuus \textstyle x_j vastaa kunkin pikselin intensiteettiä. Koska korrelaatio vierekkäisten pikselien, PCA avulla voimme approksimoida tulo paljon pienempi ulotteinen, mutta aiheuttaa hyvin vähän virheitä.
esimerkki ja matemaattinen tausta
juoksevassa esimerkissämme käytetään aineistoa \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\}, jossa \textstyle n=2 dimensional input, niin että \textstyle x^{(i)} \in \Re^2. Oletetaan, että haluamme vähentää tietoja 2 ulottuvuudet 1. (Käytännössä haluamme ehkä vähentää dataa esimerkiksi 256: sta 50: een ulottuvuuteen, mutta käyttämällä matalampaa ulottuvuutta esimerkissämme voimme visualisoida algoritmit paremmin.) Tässä on tietokokonaisuutemme:
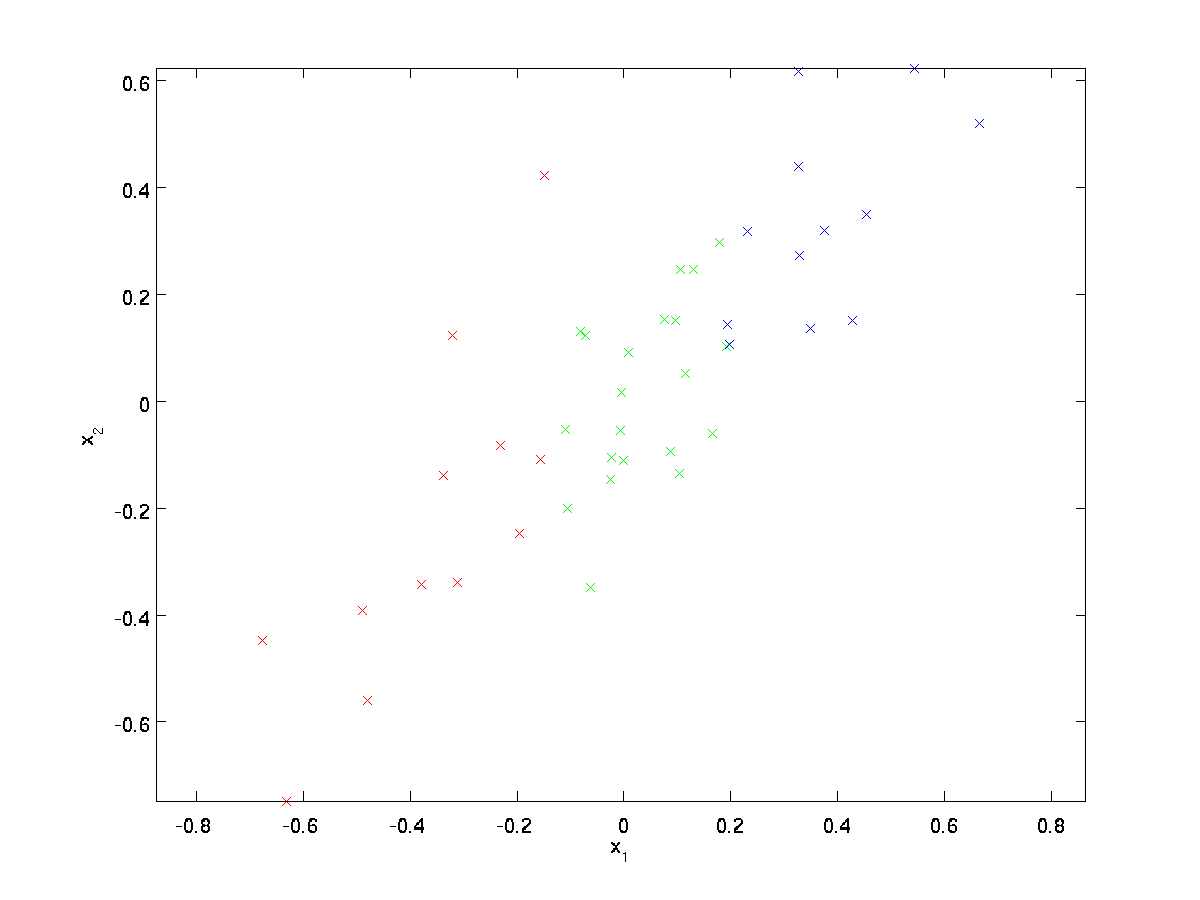
tämä tieto on jo esikäsitelty niin, että jokaisella ominaisuudella \textstyle x_1 ja \textstyle x_2 on suunnilleen sama keskiarvo (nolla) ja varianssi.
kuvitusta varten olemme myös värittäneet jokaisen pisteen yhden kolmesta väristä riippuen niiden \textstyle x_1-arvosta; algoritmi ei käytä näitä värejä, ja ne on tarkoitettu vain kuvitukseksi.
PCA löytää aliulotteisen aliavaruuden, johon voi projisoida tietomme.
aineistoa silmämääräisesti tarkasteltaessa näyttää siltä, että \textstyle u_1 on tiedon pääasiallinen vaihtelusuunta ja \textstyle u_2 toissijainen vaihtelusuunta:
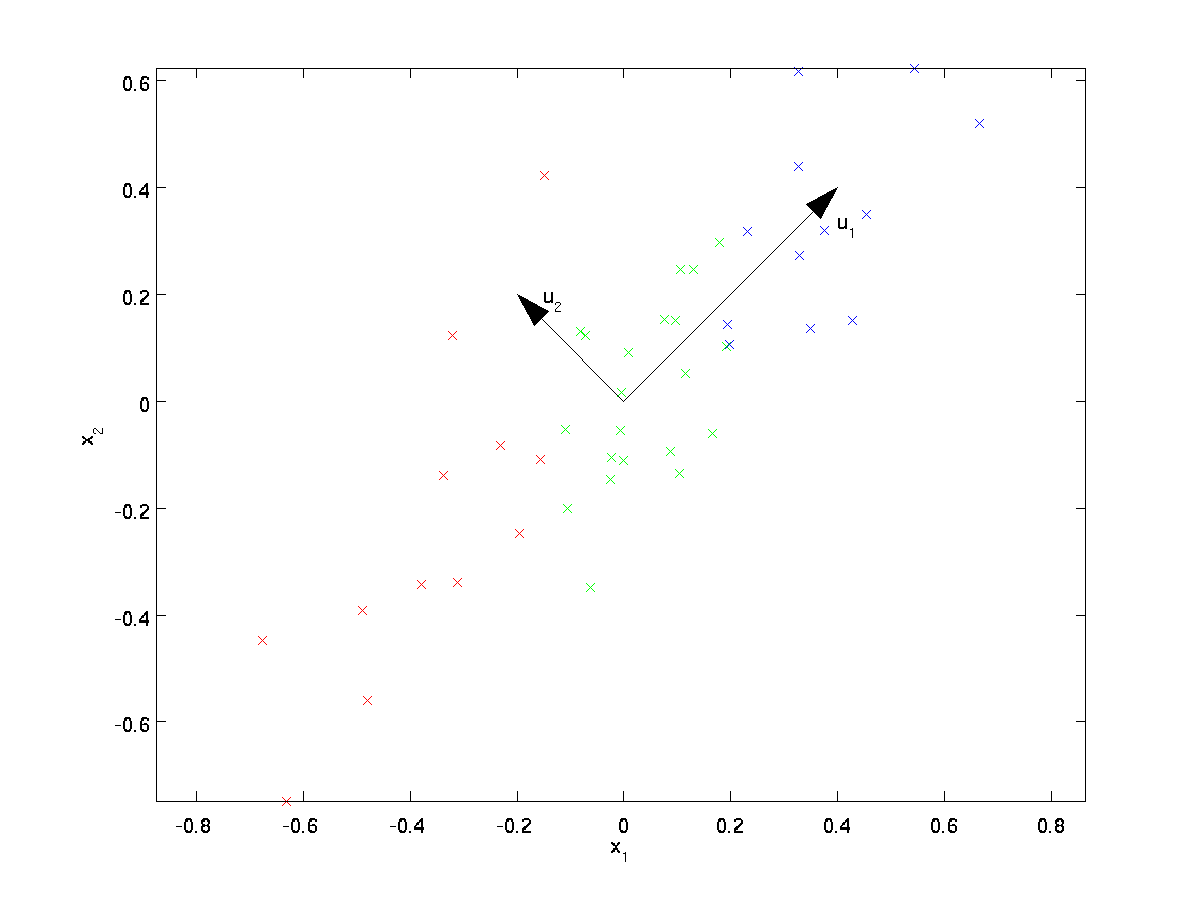
eli tieto vaihtelee paljon enemmän suuntaan \textstyle u_1 kuin \textstyle u_2. Jotta löytäisimme muodollisemmin ohjeet \textstyle u_1 ja \textstyle u_2, laskemme ensin matriisin \textstyle \Sigma seuraavasti:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}
Jos \textstyle x: llä on nollakeskiarvo, niin \textstyle \Sigma on täsmälleen \textstyle x: n kovarianssimatriisi. (symboli ”\textstyle \Sigma”, lausutaan ”Sigma”, on vakio notaatio kovarianssimatriisin ilmaisemiseksi. Valitettavasti se näyttää aivan summaussymbolilta, kuten sanassa \sum_{i = 1}^n i; mutta nämä ovat kaksi eri asiaa.)
silloin voidaan osoittaa, että \textstyle u_1—tiedon pääasiallinen vaihtelusuunta-on \textstyle \Sigman ylin (pääasiallinen) eigenvektori, ja \textstyle u_2 on toinen eigenvektori.
Huomautus: Jos olet kiinnostunut näkemään tämän tuloksen muodollisemman matemaattisen derivoinnin / perustelun, katso CS229 (Koneoppiminen) – luentomuistiinpanot PCA: sta (linkki tämän sivun alalaidassa). Sinun ei tarvitse tehdä niin seurata pitkin tätä kurssia, kuitenkin.
voit käyttää standard numeerista Lineaarialgebra-ohjelmistoa näiden eigenvektorien etsimiseen (katso Toteutusmuistiot). Lasketaan konkreettisesti \textstyle \Sigman ominaisvektorit ja pinotaan ne sarakkeisiin matriisin \textstyle U muodostamiseksi:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
esimerkkimme vektorit \textstyle u_1 ja \textstyle u_2 muodostavat uuden perustan, jolla voimme esittää dataa. Olkoon \textstyle x \in \Re^2 konkreettinen esimerkki. Silloin \textstyle u_1^TX on \textstyle x: n projektion pituus (suuruus) vektorille \textstyle u_1.
vastaavasti \textstyle u_2^Tx on \textstyle x: n suuruus, joka projisoidaan vektorille \textstyle u_2.
pyörittämällä tietoa
näin voidaan \textstyle x esittää \textstyle (u_1, u_2)-pohjalta laskemalla
\begin{align}x_{\rm rot} = U^TX = \begin{bmatrix} u_1^TX \\ u_2^TX \end{bmatrix} \end{align}
(alaindeksi ”rot” tulee havainnosta, että tämä vastaa kiertoa (ja mahdollisesti heijastusta) alkuperäisten tietojen.) Otetaan koko harjoitussarja ja lasketaan \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} jokaiselle \textstyle I: lle.:

Tämä on \textstyle u_1,\textstyle u_2-periaatteeseen käännetty harjoitussarja. Yleistapauksessa \textstyle U^TX on \textstyle u_1,\textstyle u_2,…, \textstyle u_n.
yksi \textstyle U: n ominaisuuksista on, että se on ”ortogonaalinen” matriisi, mikä tarkoittaa, että se täyttää \textstyle U^tu = UU^t = I. Jos siis joskus on siirryttävä käännetyistä vektoreista \textstyle x_{\rm rot} takaisin alkuperäiseen dataan \textstyle x, voit laskea
\begin{align}x = U x_{\rm Rot} ,\end{align}
koska \textstyle U x_{\rm Rot} = UU^t x = x.
vähentämällä Datamuuttujaa
näemme,että datan pääasiallinen vaihtelusuunta on ensimmäinen dimensio \textstyle x_{\RM Rot, 1} Tätä käännettyä dataa. Jos siis haluamme supistaa tämän tiedon yhteen ulottuvuuteen, voimme asettaa
\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^TX^{(i)} \in \Re.\end{align}
yleisemmin, jos \textstyle x \in \Re^n ja haluamme supistaa sen \textstyle k-ulotteiseksi esitykseksi \textstyle \tilde{x} \in \Re^k (Missä k < n), otamme \textstyle x_ {\rm rot}: n ensimmäiset\textstyle k-osat, jotka vastaavat ylimpiä \textstyle k-variaatiosuuntia.
toinen tapa selittää PCA on, että \textstyle x_{\rm rot} on \textstyle n-ulotteinen vektori, jossa ensimmäiset komponentit ovat todennäköisesti suuria (esim., esimerkissämme näimme, että \textstyle x_{\rm rot, 1}^{(i)} = u_1^TX^{(i)} ottaa kohtuullisen suuret arvot useimmille esimerkeille \textstyle i), ja myöhemmät komponentit ovat todennäköisesti pieniä (esim.esimerkissämme \textstyle x_{\rm rot, 2}^{(i)} = u_2^TX^{(i)} oli todennäköisemmin pieniä). Mitä PCA tekee, se pudottaa \textstyle x_{\rm rot}: n myöhemmät (pienemmät) komponentit ja vain approksimoi Ne 0: n kanssa. konkreettisesti \textstyle \tilde{x}: n määritelmä voidaan saavuttaa myös käyttämällä approksimaatiota \textstyle x_{\rm rot}: iin, jossa kaikki muut paitsi ensimmäinen \textstyle k: N osat ovat nollia. Toisin sanoen:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot, 1} \\\vdots \\ x_{\rm rot,K} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,K+1} \\\vdots \\ x_{\rm Rot,n} \end{bmatrix}= x_{\rm rot} \end{align}
esimerkissämme saadaan seuraava \textstyle \tilde{X} (käyttäen \textstyle N=2,K=1):

kuitenkin, koska \textstyle \tilde{x}: n lopulliset \textstyle n-k-komponentit, kuten edellä on määritelty, olisivat aina nolla, näitä nollia ei tarvitse pitää ympärillä, joten määrittelemme \textstyle \tilde{x} \textstyle k-ulotteiseksi vektoriksi, jossa on vain ensimmäiset \textstyle k (ei-nolla) komponentit.
Tämä selittää myös sen, miksi halusimme ilmaista tietomme \textstyle u_1, u_2, \ldots, u_n basis: päättämällä, mitkä osat säilytetään, tulee vain pitää ylimmät \textstyle k komponentit. Kun teemme tämän, sanomme myös, että olemme ” säilyttää alkuun \ textstyle k PCA (tai pääasiallinen) komponentit.”
tietojen likiarvon palauttaminen
nyt \textstyle \tilde{x} \in \Re^k on alempiulotteinen, ”pakattu” esitys alkuperäisestä \textstyle x \in \Re^n. kun otetaan huomioon \textstyle \tilde{x}, miten voimme palauttaa likiarvon \textstyle \hat{x} alkuperäisen arvon \textstyle x? Aiemmasta osasta tiedämme, että \textstyle x = U x_{\rm rot}. Lisäksi voimme ajatella \textstyle \tilde{x}: n likiarvona \textstyle x_{\rm rot}: lle, jossa olemme asettaneet viimeiset \textstyle n-k: n komponentit nolliksi. Näin ollen, kun \textstyle \tilde{x} \in \Re^k, voimme täyttää sen \textstyle n-k nollilla saadaksemme approksimaatiomme \textstyle x_{\rm rot} \in \Re^n. lopuksi esikertomme \textstyle U: lla saadaksemme approksimaatiomme \textstyle x: ään. konkreettisesti saamme
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{X}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^K u_i \tilde{x}_i. \end{align}
yllä oleva lopullinen tasa-arvo tulee aiemmin annetusta \textstyle U: n määritelmästä. (Käytännön toteutuksessa emme itse asiassa nollaisi pad \textstyle \tilde{x} ja sitten kertoisimme \textstyle U: lla, koska se merkitsisi monien asioiden kertomista nollilla; sen sijaan kertoisimme \textstyle \tilde{x} \in \Re^k \textstyle U: n ensimmäisillä \textstyle k-sarakkeilla kuten viimeisessä lausekkeessa.) Soveltamalla tätä tietojoukkoomme saamme seuraavan kaavion \textstyle \hat{x}:
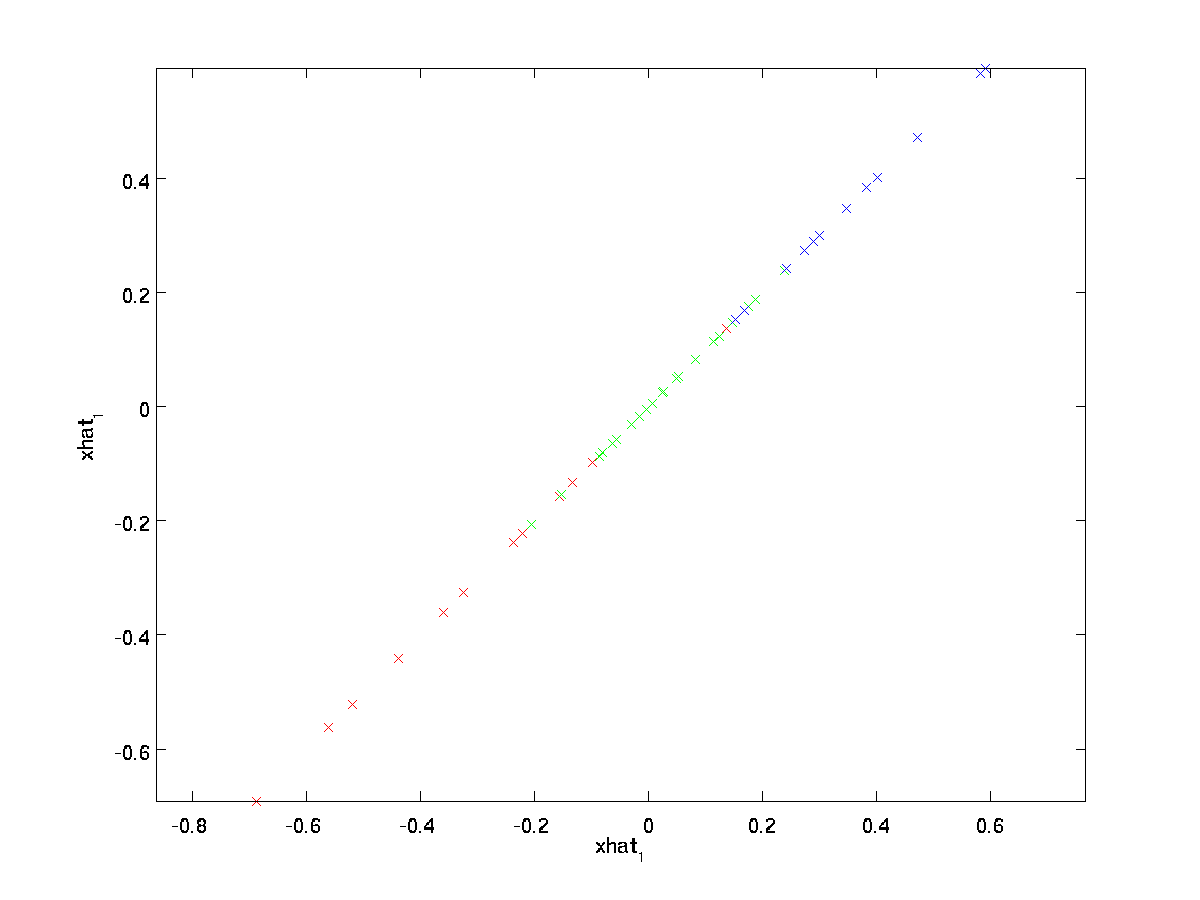
käytämme siis 1-ulotteista likiarvoa alkuperäiseen aineistoon.
Jos harjoittelet automaattista kooderia tai muuta valvomatonta ominaisuusoppimisalgoritmia, algoritmin käyttöaika riippuu syötteen ulottuvuudesta. Jos syötät \textstyle \tilde{x} \in \Re^k oppimisalgoritmiisi \textstyle x: n sijaan, harjoittelet alempiulotteista syötettä, jolloin algoritmisi saattaa toimia huomattavasti nopeammin. Monille tietokokonaisuuksille alempi ulotteinen \ textstyle \tilde{x} – esitys voi olla erittäin hyvä approksimaatio alkuperäiseen, ja käyttämällä PCA tällä tavalla voi merkittävästi nopeuttaa algoritmia ja ottaa käyttöön hyvin vähän approksimaatiovirhe.
säilytettävien komponenttien määrä
miten asetamme \textstyle k: n; eli kuinka monta PCA-komponenttia meidän tulee säilyttää? Meidän yksinkertainen 2 ulotteinen esimerkki, se tuntui luonnolliselta säilyttää 1 ulos 2 komponentteja, mutta suurempi ulotteinen data, tämä päätös on vähemmän triviaali. Jos \textstyle k on liian suuri, emme pakkaa tietoja paljoa; \textstyle k=n: n raja-alueella käytämme vain alkuperäistä dataa (mutta käännämme eri perustalle). Kääntäen, jos \textstyle k on liian pieni, niin saatamme käyttää Erittäin huono approksimaatio tietoja.
päättääksemme, miten \textstyle k asetetaan, tarkastelemme yleensä \textstyle k: n eri arvoille ”’varianssin prosenttiosuus”’. konkreettisesti, jos \textstyle k=n, meillä on tarkka likiarvo aineistolle, ja sanomme, että 100% varianssista säilyy. Ts., kaikki alkuperäisen tiedon vaihtelu säilytetään. Kääntäen, jos \textstyle K=0, niin olemme approksimoimassa kaikkia tietoja nollavektorilla, jolloin 0% varianssista säilyy.
yleisemmin, olkoot \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n \textstyle \Sigman (järjestetty alenevaan järjestykseen) yksikköarvo siten, että \textstyle \lambda_j on yksikköarvo, joka vastaa yksikköarvoa \textstyle u_j. jos säilytämme \textstyle k: n pääkomponentit, varianssin prosenttiosuus saadaan:
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}.\end{align}
yllä olevassa yksinkertaisessa 2D-esimerkissämme \textstyle \lambda_1 = 7.29 ja \textstyle \lambda_2 = 0.69. Siten pitämällä vain \textstyle k=1 pääkomponentit säilytimme \textstyle 7.29/(7.29+0.69) = 0.913, tai 91,3% varianssista.
pidetyn varianssin prosenttiosuuden muodollisempi määritelmä ei kuulu näiden huomautusten soveltamisalaan. On kuitenkin mahdollista osoittaa, että \textstyle \lambda_j = \sum_{i = 1}^m x_{\rm rot,J}^2. Näin ollen, jos \textstyle \lambda_j \approx 0, tämä osoittaa, että \textstyle x_{\rm rot, j} on yleensä lähellä 0 joka tapauksessa, ja menetämme suhteellisen vähän approksimoimalla sitä vakiolla 0. Tämä selittää myös, miksi säilytämme ylimmät pääkomponentit (jotka vastaavat suurempia arvoja \textstyle \lambda_j) alimpien sijaan. Ylimmät pääkomponentit \textstyle x_{\rm rot, j} ovat niitä, jotka ovat muuttuvampia ja joilla on suuremmat arvot ja joille aiheutuisi suurempi likiarvovirhe, jos asettaisimme ne nollaan.
kuvien tapauksessa yksi yleinen heuristinen on valita \textstyle k niin, että varianssista säilyy 99%. Toisin sanoen valitsemme \textstyle k: n pienimmän arvon, joka täyttää
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0,99. \end{align}
sovelluksesta riippuen, jos olet valmis aiheuttamaan jonkin lisävirheen, käytetään joskus myös 90-98%: n arvoja. Kun kuvailet muille, miten sovellit PCA, sanomalla, että valitsit \textstyle k säilyttää 95% varianssi on myös paljon helpommin tulkittava kuvaus kuin sanomalla, että olet säilyttänyt 120 (tai mikä tahansa muu määrä) komponentteja.
PCA kuvilla
jotta PCA toimisi, yleensä haluamme, että jokaisella ominaisuudella \textstyle x_1, x_2, \ldots, x_n on samanlainen arvoalue kuin muilla (ja keskiarvon olevan lähellä nollaa). Jos olet käyttänyt PCA: ta aiemmin muissa sovelluksissa, saatat siksi olla erikseen esikäsitellyt jokaisen ominaisuuden nollakeskiarvoksi ja yksikkövarianssiksi arvioimalla erikseen kunkin ominaisuuden keskiarvon ja varianssin \textstyle x_j. tämä ei kuitenkaan ole esikäsittely, jota sovellamme useimpiin kuvatyyppeihin. Erityisesti oletetaan, että koulutamme algoritmiamme ”’natural images”’, niin että \textstyle x_j on pikselin arvo \textstyle J. By” natural images ” me epävirallisesti tarkoitamme kuvan tyyppiä, jonka tyypillinen eläin tai henkilö saattaa nähdä elinaikanaan.
Huomautus: Yleensä käytämme kuvia ulkona kohtauksia ruoho, puut, jne., ja leikata pieniä (sanoa 16×16) kuva laastaria satunnaisesti näistä kouluttaa algoritmia. Mutta käytännössä useimmat ominaisuus oppimisen algoritmit ovat erittäin vankka tarkka kuvan se on koulutettu, joten useimmat kuvat otettu normaalilla kameralla, niin kauan kuin ne eivät ole liian epäselvä tai on outoja esineitä, pitäisi toimia.
luonnollisilla kuvilla harjoiteltaessa ei ole juurikaan järkeä arvioida erillistä keskiarvoa ja varianssia jokaiselle pikselille, koska kuvan yhden osan tilastojen pitäisi (teoriassa) olla samat kuin minkä tahansa muun.
tätä kuvien ominaisuutta kutsutaan nimellä ”’ stationarity.””
yksityiskohtaisesti, jotta PCA toimisi hyvin, epävirallisesti edellytämme, että (i) ominaisuuksilla on suunnilleen nolla keskiarvo, ja (ii) eri ominaisuuksilla on samanlaiset varianssit keskenään. Luonnon kuvia, (ii) on jo tyytyväinen jopa ilman varianssi normalisointi, joten emme suorita mitään varianssi normalisointi.
(Jos harjoittelet äänidataa-sano, spektrografeja—tai tekstidataa-sano, sanapussia-vektoreita—emme yleensä suorita myöskään varianssi normalisointia.)
itse asiassa PCA on invariantti datan skaalaukselle, ja palauttaa samat eigenvektorit riippumatta tulon skaalauksesta. Muodollisemmin, jos kerrot jokaisen ominaisuusvektorin \textstyle x jollakin positiivisella luvulla (jolloin jokainen ominaisuus skaalataan jokaisessa harjoitusesimerkissä samalla luvulla), PCA: n tuloste eigenvektorit eivät muutu.
niin, emme käytä varianssi normalisointi. Ainoa normalisointi meidän täytyy suorittaa sitten on tarkoita normalisointi, jotta varmistetaan, että ominaisuudet ovat keskimäärin noin nolla. Sovelluksesta riippuen emme useinkaan ole kiinnostuneita siitä, kuinka kirkas kokonaissyöttökuva on. Esimerkiksi objektintunnistustehtävissä kuvan yleinen kirkkaus ei vaikuta siihen, mitä kohteita kuvassa on. Muodollisemmin Emme ole kiinnostuneita kuvan laastarin keskimääräisestä intensiteettiarvosta; näin voimme vähentää tämän arvon keskiarvon normalisoinnin muotona.
konkreettisesti, jos \textstyle x^{(i)} \in \Re^{n} ovat 16×16-kuvapäivityksen (\textstyle n=256) (harmaasävy) intensiteettiarvot, voimme normalisoida jokaisen kuvan intensiteetin \textstyle x^{(i)} seuraavasti:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := x^{(i)} _j – \mu^{(i)}
kaikille \textstyle j
huomaa, että kaksi yllä olevaa askelta tehdään erikseen jokaiselle kuvalle \textstyle x^{(i)}, ja että \textstyle \mu^{(I)} Tässä on kuvan \textstyle x^{(i)} keskimääräinen intensiteetti. Erityisesti tämä ei ole sama asia kuin keskiarvon estimointi erikseen jokaiselle pikselille \textstyle x_j.
jos koulutat algoritmiasi muilla kuin luonnollisilla kuvilla (esimerkiksi käsinkirjoitettujen merkkien kuvat tai kuvia yksittäisistä yksittäisistä kohteista, jotka on keskitetty valkoiselle taustalle), muunlaista normalisointia kannattaa harkita, ja paras valinta voi olla sovellusriippuvainen. Mutta kun koulutusta luonnon kuvia, käyttämällä per-kuva mean normalisointi menetelmä annetaan yhtälöt edellä olisi kohtuullinen oletus.
valkaisu
olemme käyttäneet PCA: ta pienentääksemme datan ulottuvuutta. On läheistä sukua esikäsittely vaiheessa kutsutaan valkaisuun (tai, joissakin muissa kirjallisuus, sphering), joka tarvitaan joitakin algoritmeja. Jos koulutamme kuvia, raaka-tulo on tarpeeton,koska vierekkäiset pikseliarvot korreloivat hyvin. Tavoitteena valkaisuun on tehdä panos vähemmän tarpeeton; muodollisemmin, meidän desiderata on, että meidän oppimisen algoritmit näkee koulutus syöttää, jossa (i) ominaisuudet ovat vähemmän korreloivat keskenään, ja (ii) ominaisuudet kaikki on sama varianssi.
2D-esimerkki
kuvaamme ensin valkaisua käyttäen edellistä 2D-esimerkkiämme. Sitten kuvataan, miten tämä voidaan yhdistää silottamiseen ja lopuksi, miten tämä voidaan yhdistää kumppanuus-ja yhteistyösopimukseen.
miten voimme tehdä syöteominaisuuksistamme keskenään sopimattomia? Olimme tehneet tämän jo laskiessamme \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}.
toistaen edellistä lukuamme \textstyle x_{\rm rot}:

tämän tiedon kovarianssimatriisin antaa:
\begin{align}\begin{bmatrix}7.29 && 0, 69\end{bmatrix}.\end{align}
(Huomautus: Teknisesti monet tämän osion väittämät ”kovarianssista” ovat tosia vain, jos aineistolla on nolla keskiarvoa. Tämän osion loppuosassa otamme tämän olettamuksen implisiittiseksi lausunnoissamme. Kuitenkin, vaikka tietojen keskiarvo ei ole täsmälleen nolla, intuitiot esitämme täällä silti pitää paikkansa, joten tämä ei ole jotain, että sinun pitäisi huolehtia.)
ei ole sattumaa, että lävistäjät ovat \textstyle \lambda_1 ja \textstyle \lambda_2. Lisäksi off-diagonaalinen merkinnät ovat nolla; siten \textstyle x_{\rm rot, 1} ja \textstyle x_{\rm rot,2} ovat oikosulkemattomia, mikä täyttää yhden valkoistettujen tietojen toiveistamme (että ominaisuudet eivät korreloi yhtä paljon).
jotta jokaisella syöteominaisuudellamme olisi yksikkövarianssi, voimme yksinkertaisesti uudelleenvalaista jokaisen ominaisuuden \textstyle x_{\rm rot,i} by \textstyle 1 / \sqrt{\lambda_i}. Konkreettisesti määrittelemme valkaistut tietomme \textstyle x_{\rm PCAwhite} \in \Re^n seuraavasti:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}
merkitään \textstyle x_{\rm PCAwhite}, saadaan:

tällä tiedolla on nyt kovarianssi, joka vastaa identiteettimatriisia \textstyle I. sanomme, että \textstyle x_{\rm PCAwhite} on PCA-valkaistu versiomme datasta: \textstyle x_{\RM PCAwhite}: n eri komponentit ovat oikolukemattomia ja niillä on yksikkövarianssi.
valkaisu yhdistettynä dimensionaalisuuden vähentämiseen. Jos haluat, että tieto on valkaistua ja aliulotteista kuin alkuperäinen syöte, voit halutessasi säilyttää vain \textstyle x_ {\rm PCAwhite}: n ylimmät\textstyle k-komponentit. Kun yhdistämme PCA-valkaisun regularisointiin (kuvattu myöhemmin), \textstyle x_{\rm PCAwhite}: n viimeiset komponentit ovat lähes nollassa joka tapauksessa, ja siten ne voidaan turvallisesti pudottaa.
ZCA Whitening
lopulta käy ilmi, että tämä tapa saada tieto kovarianssitunnukseksi \textstyle I ei ole ainutlaatuinen. Konkreettisesti, jos \textstyle R on mikä tahansa ortogonaalinen matriisi, niin että se täyttää \textstyle RR^T = R^TR = I (vähemmän muodollisesti, jos \textstyle R on kierto – /heijastusmatriisi), niin \textstyle r\, x_{\rm PCAwhite}: llä on myös identiteetin kovarianssi.
ZCA-valkaisussa valitsemme \textstyle R = U. määrittelemme
\begin{align}x_{\rm ZCAwhite} = U x_{\RM PCAwhite}\end{align}
piirtämällä \textstyle x_{\RM ZCAwhite}, saamme:

se voi osoittakaa, että kaikista \textstyle r: n mahdollisista valinnoista tämä Vuorotteluvalinta saa \textstyle x_{\rm zcawhite}: n olemaan mahdollisimman lähellä alkuperäistä Syötetietoa \textstyle x.
käytettäessä ZCA-valkaisua (toisin kuin PCA-valkaisua) pidämme yleensä kaikki \textstyle N: n mitat, emmekä yritä pienentää sen ulottuvuutta.
Regularizaton
toteutettaessa PCA-valkaisua tai ZCA-valkaisua käytännössä, joskus osa eigenvalueista \textstyle \lambda_i on numeerisesti lähellä 0: ta, ja siten skaalausvaihe, jossa jaamme \sqrt{\lambda_i}: llä, sisältäisi jakamisen arvolla, joka on lähellä nollaa; tämä voi aiheuttaa tietojen räjähtämisen (ottaa suuria arvoja) tai olla muuten numeerisesti epävakaa. Käytännössä toteutamme siis tämän skaalausvaiheen käyttämällä pientä määrää säännönmukaistamista ja lisäämme pienen vakion \textstyle \epsilon eigenvaluesiin ennen kuin otamme niiden neliöjuuren ja käänteisarvon:
\begin{align}x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i + \epsilon}}.\end{align}
kun \textstyle x ottaa arvot \textstyle: n ympärille, \textstyle \epsilon \approx 10^{-5}: n arvo voi olla tyypillinen.
kuvien tapauksessa \textstyle \Epsilonin lisääminen tähän vaikuttaa myös siihen, että syötetty kuva hieman tasoittuu (tai alipäästösuodatetaan). Tällä on myös toivottava vaikutus poistaa artefakteja, jotka johtuvat siitä, miten Pikselit on asetettu kuvaan, ja se voi parantaa opittuja ominaisuuksia (yksityiskohdat ovat näiden muistiinpanojen soveltamisalan ulkopuolella).
ZCA-valkaisu on tiedon esikäsittelyn muoto, jolla se kartoitetaan \textstyle x: stä \textstyle x_{\rm ZCAwhite}. On käynyt ilmi, että tämä on myös karkea malli siitä, miten biologinen silmä (verkkokalvo) käsittelee kuvia. Erityisesti, kun silmäsi havaitsee kuvia, Useimmat vierekkäiset ”Pikselit” silmässäsi havaitsevat hyvin samanlaisia arvoja, koska kuvan vierekkäiset osat yleensä korreloivat voimakkaasti intensiteetiltään. On siis tuhlausta, että silmäsi joutuu lähettämään jokaisen pikselin erikseen (näköhermon kautta) aivoihisi. Sen sijaan verkkokalvo suorittaa decorrelation-operaation (tämä tapahtuu verkkokalvon neuronien kautta, jotka laskevat toiminnon nimeltä ”On center, off surround/off center, on surround”), joka on samanlainen kuin ZCA. Tämä johtaa vähemmän tarpeeton esitys syötteen kuva, joka sitten lähetetään aivoihin.
PCA-valkaisun toteuttaminen
tässä osiossa tiivistämme PCA -, PCA-valkaisu-ja ZCA-valkaisualgoritmit ja kuvailemme myös, miten voit toteuttaa ne tehokkailla Lineaarialgebra-kirjastoilla.
ensin on varmistettava, että aineistolla on (likimain) nollakeskiarvo. Luonnollisten kuvien osalta saavutamme tämän (suunnilleen)vähentämällä kunkin kuvapaikan keskiarvon.
saavutamme tämän laskemalla kunkin laastarin keskiarvon ja vähentämällä sen jokaisesta laastarista. Matlabissa tämä voidaan tehdä käyttämällä
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);seuraavaksi on laskettava \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. jos toteutat tämän Matlabissa (tai vaikka toteutat tämän C++: ssa, Javassa, jne., mutta on pääsy tehokkaaseen lineaarialgebran kirjastoon), tekee sen eksplisiittisenä summana tehottomaksi. Sen sijaan voimme laskea tämän kertaheitolla, kuten
sigma = x * x' / size(x, 2);(Tarkista matematiikka itse oikeellisuuden varalta.) Tässä oletamme, että x on tietorakenne, joka sisältää yhden harjoitusesimerkin saraketta kohti (eli x on \textstyle n-by-\textstyle m-matriisi).
seuraavaksi PCA laskee \Sigman eigenvektorit. Voit tehdä tämän käyttämällä Matlab eig-toimintoa. Koska \Sigma on symmetrinen positiivinen puolimääräinen matriisi, se on kuitenkin numeerisesti luotettavampi tehdä svd-funktion avulla. Konkreettisesti, jos toteutat
= svd(sigma);niin matriisi U sisältää \Sigman eigenvektorit (yksi eigenvektori per sarake, järjestetty järjestyksessä ylhäältä alas eigenvektori), ja matriisin s lävistäjät sisältävät vastaavat eigenvektorit (lajiteltu myös alenevassa järjestyksessä). Matriisi V on yhtä suuri kuin U, ja voidaan turvallisesti sivuuttaa.
(Huom.: Svd-funktio itse asiassa laskee matriisin yksikkövektorit ja yksikköarvot, jotka symmetrisen positiivisen puolimääräisen matriisin erikoistapauksessa-mikä on kaikki, mitä tässä on kyse—ovat yhtä suuret kuin sen eigenvektorit ja eigenvalues. Täydellinen keskustelu yksittäisistä vektoreista vs. eigenvektoreista on näiden muistiinpanojen ulottumattomissa.)
voit laskea \textstyle x_{\rm rot} ja \textstyle \tilde{x} seuraavasti:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keeptämä antaa PCA-esityksesi tiedoista muodossa \textstyle \tilde{x} \in \Re^k. Muuten, jos x on \textstyle n-by-\textstyle m-matriisi, joka sisältää kaikki harjoitustietosi, tämä on vektoroitu toteutus, ja yllä olevat lausekkeet toimivat myös x_{\rm rot} ja \tilde{x} koko koulutussarjasi laskemiseen yhdellä kertaa. Tuloksilla x_{\rm rot} ja \tilde{x} on yksi sarake, joka vastaa kutakin harjoitusesimerkkiä.
PCA-valkaistun datan laskemiseen \textstyle x_{\rm PCAwhite}, käytä
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;koska S: n lävistäjä sisältää ominaisarvot \textstyle \lambda_i, tämä osoittautuu kompaktiksi tavaksi laskea \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,I} }{\sqrt{\lambda_i}} samanaikaisesti kaikille \textstyle I: lle.
lopuksi voit laskea myös ZCA: n valkaistut tiedot \textstyle x_{\RM zcawhite} as:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;