Il Principio di Franck-Condon descrive le intensità delle transizioni vibroniche, o l’assorbimento o l’emissione di un fotone. Afferma che quando una molecola sta subendo una transizione elettronica, come la ionizzazione, la configurazione nucleare della molecola non subisce cambiamenti significativi. Ciò è dovuto infatti al fatto che i nuclei sono molto più massicci degli elettroni e la transizione elettronica avviene più velocemente di quanto i nuclei possano rispondere. Quando il nucleo si riallinea con la nuova configurazione elettronica, la teoria afferma che deve subire una vibrazione.
Se descriviamo il passaggio in verticale da terra eccitato elettronici stato che si verificano da una funzione d’onda vibrazionale che dà una distribuzione di probabilità di trovare i nuclei in una regione di spazio siamo in grado di determinare la probabilità di un dato livello vibrazionale dalla sovrapposizione integrale \(S_{v’,v}\), che fornisce la sovrapposizione della funzione d’onda vibrazionale della terra e stato eccitato. I numeri quantici \(v’\) si riferiscono allo stato fondamentale e i numeri quantici \(v\) si riferiscono allo stato eccitato. La probabilità di transizione può essere separata in parti elettroniche e nucleari usando l’approssimazione di Condon.
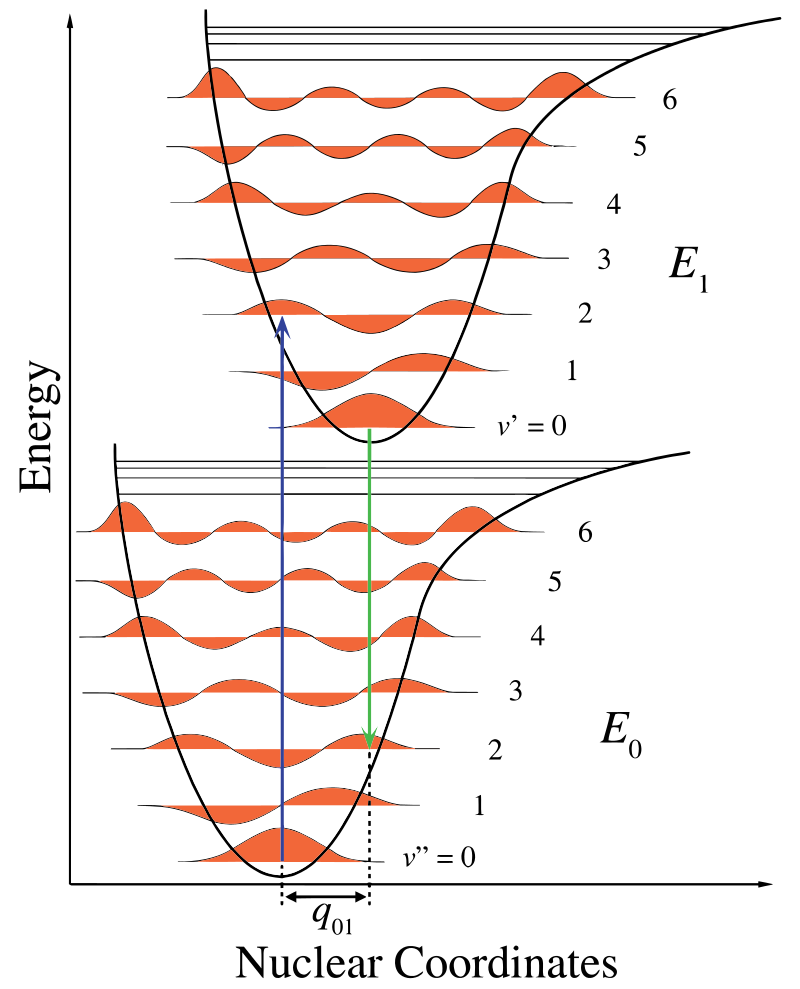
In figura \(\PageIndex{1}\), l’asse nucleare mostra una conseguenza della separazione internucleare e la transizione vibronica è indicata dalle frecce verticali blu e verdi. Questa figura dimostra tre cose:
- Un assorbimento porta ad uno stato di energia superiore,
- la fluorescenza porta ad uno stato di energia inferiore e
- lo spostamento delle coordinate nucleari tra il terreno e lo stato eccitato è indicativo di una nuova posizione di equilibrio per il potenziale di interazione nucleare. Il fatto che la freccia di fluorescenza sia più corta dell’assorbimento indica che ha meno energia o che la sua lunghezza d’onda è più lunga.
L’approssimazione Condon classica
L’approssimazione Condon è l’ipotesi che la transizione elettronica avvenga su una scala temporale breve rispetto al moto nucleare in modo che la probabilità di transizione possa essere calcolata in una posizione nucleare fissa.
Questo cambiamento di vibrazione viene mantenuto durante uno stato chiamato eccitazione elettronica rapida. Le forze coulombiche risultanti producono un equilibrio come mostrato nella figura per i nuclei definiti un punto di svolta. Il punto di svolta può essere mappato disegnando una linea verticale dal minimo della curva inferiore all’intersezione dello stato elettronico superiore. Questa procedura è definita una transizione verticale ed è stata discussa prima nel contesto della spettroscopia fotoelettronica (un altro spettroscopio elettronico)..
Il Principio di Franck-Condon spiega le intensità relative delle transizioni vibroniche mettendo in relazione la probabilità di una transizione vibrazionale con la sovrapposizione delle funzioni d’onda vibrazionali. Afferma che la probabilità che si verifichi una transizione vibrazionale è ponderata dall’integrale di sovrapposizione di Franck-Condon:
\
All’interno dell’approssimazione di Franck-Condon, i nuclei sono considerati” fissi ” durante le transizioni elettroniche. Pertanto, le transizioni elettroniche possono essere considerate transizioni verticali su curve elettroniche di energia potenziale (transizioni viericali in Figura \(\PageIndex{1}\)).
Il principio di Franck-Condon Quantistico
Il principio di Franck-Condon ha sia un’applicazione classica che quantistica. Classicamente, il principio di Franck-Condon è l’approssimazione che una transizione elettronica è più probabile che si verifichi senza cambiamenti nelle posizioni dei nuclei nell’entità molecolare e nel suo ambiente. Lo stato risultante è chiamato stato Franck-Condon, e la transizione coinvolta, una transizione verticale. La formulazione meccanica quantistica di questo principio è che l’intensità di una transizione vibronica è proporzionale al quadrato dell’integrale di sovrapposizione tra le funzioni d’onda vibrazionali dei due stati coinvolti nella transizione.
Il principio di Franck-Condon si basa sull’approssimazione di Born-Oppenheimer, che consente la separazione delle funzioni d’onda elettroniche \(q\) e nucleari \(Q\) data la funzione d’onda totale.
\
Poiché l’operatore di transizione,\(\hat {\mu} (q)\), dipende solo dal componente elettronico, i componenti nucleari possono essere separati dall’integrale del momento di transizione che determina la probabilità che si verifichi la transizione:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nucleare sovrapposizione}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
Se il nucleare si sovrappongono integrale è zero per questa fase di transizione, quindi il passaggio non potrà essere osservato, a prescindere dalla grandezza dell’elettronica fattore.
\(S_{00}\) Transizione Valutata all’interno del Modello Oscillatore Armonico
La sovrapposizione nucleare per la transizione zero-zero \(S_{00}\) può essere calcolata semplicemente usando la definizione della forma gaussiana delle funzioni d’onda dell’oscillatore armonico.
Il punto di zero funzione d’onda nel terreno elettronici di stato
\
Il punto di zero funzione d’onda nella eccitato elettronico di stato
\
dove
- \(\alpha = \dfrac{\sqrt{mk}}{\editormaniglie}\)
- \(R_e\) è l’equilibrio lunghezza di legame in terra stato di elettronica
- \(Q_e\) è l’equilibrio lunghezza di legame in eccitato stato di elettronica
Il nucleare si sovrappongono integrale è
\
L’esponente nell’Equazione \(\ref{FC1}\) può essere espansa
\
e si usa
\
e
\
sostituire e completare il quadrato all’interno dell’integrale. Possiamo esprimere
\.\]
Quindi, l’integrale nell’equazione \(\ref{FC2}\) è
\
L’integrale è un integrale gaussiano. Si può dimostrare che, se lasciamo che \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) allora \(dz = \sqrt{\alpha} dR\) e l’integrale diventa
\
questo integrale è stato risolto già da una tabella di integrali, Equazione \(\ref{FC3}\) diventa
\
Si dovrebbe seguire la stessa procedura per il calcolo di tale sovrapposizione di zero a livello di vibrazioni nel terreno per il primo eccitato livello vibrazionale dello stato eccitato: \(S_{01}\).
\(S_{01}\) la Transizione Valutata nel Modello dell’Oscillatore Armonico
calcolare la sovrapposizione di zeroth terreno a livello statale (\(v=0\)) con il primo stato eccitato livello (\(v’=1\)) usiamo il polinomio di Hermite \(H_1(x) =2x\) per descrivere lo stato eccitato funzione d’onda (vedi qui per una recensione su oscillatore armonico funzioni d’onda degli). Qui \(x = \ sqrt {\alpha} (R-Q_e)\).
\
con il “punto zero” funzione d’onda nel terreno elettronici di stato
\
Il primo stato eccitato di funzione d’onda nella eccitato elettronico di stato
\
La sovrapposizione di zeroth terreno a livello statale con il primo stato eccitato (livello di Equazione \(\ref{FC01}\)) è quindi
\
e
\
Lo stesso le sostituzioni possono essere effettuate come sopra, in modo che l’integrale può essere scritto come (non mostrato e dimostrato in compiti a casa) e il risultato finale è
\
Potremmo continuare e calcolare quella sovrapposizione del livello zero nello stato fondamentale con tutti i livelli vibrazionali della luce più alti: \(S_{02}\), \(S_{03}\), ecc. Ogni termine corrisponde a una transizione con un’energia diversa poiché i livelli vibrazionali hanno energie diverse. La banda di assorbimento ha quindi l’aspetto di una progressione (una progressione di Franck-Condon) di transizioni tra diversi livelli ciascuno con una propria probabilità.
Progressioni di Franck-Condon
Per comprendere il significato della formula di cui sopra per il fattore FC, esaminiamo una superficie di energia potenziale di terra e di stato eccitato a \(T = 0\) Kelvin. Di seguito sono riportati due stati separati da 8.000 cm-1 in energia. Questa è la separazione di energia tra i fondi dei loro pozzi potenziali, ma anche tra i rispettivi livelli di energia a punto zero. Supponiamo che il numero d’onda della modalità vibrazionale sia 1.000 cm-1 e che la lunghezza del legame sia aumentata a causa del fatto che un elettrone viene rimosso da un orbitale di legame e posto in un orbitale anti-legame su eccitazione elettronica.
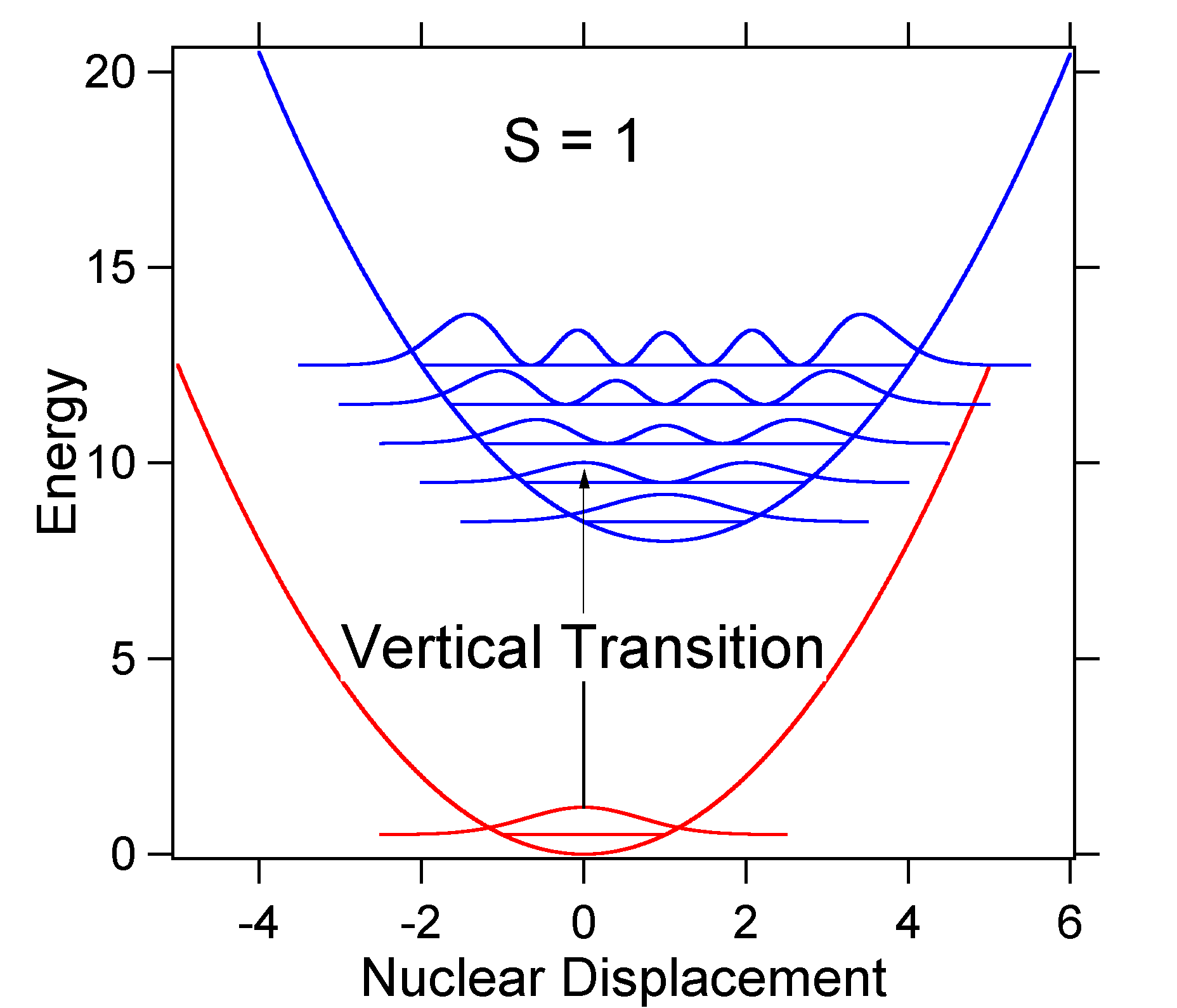
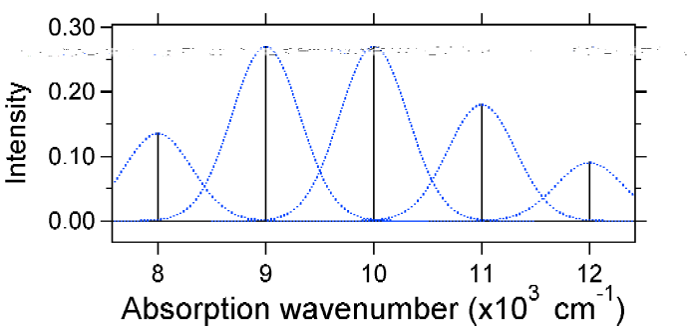
Secondo il modello precedente per il fattore Franck-Condon genereremmo uno spettro “stick” (Figura \(\PageIndex{3}\)) dove ogni transizione vibrazionale è infinitamente stretta e la transizione può avvenire solo quando \(E = h\nu\) esattamente. Ad esempio, le superfici di energia potenziale sono state date per S = 1 e la probabilità di transizione ad ogni livello è data dai bastoncini (neri) nella figura seguente.
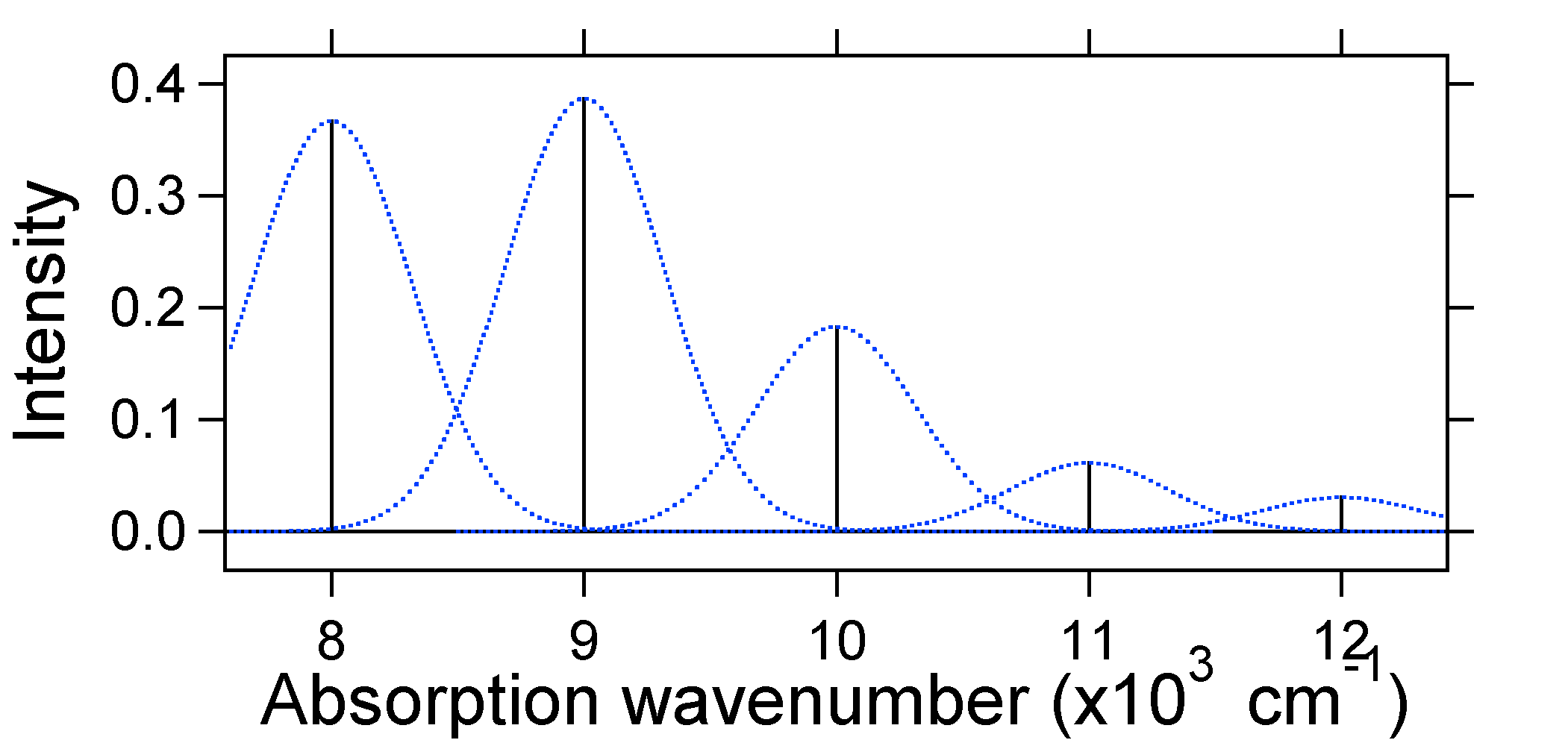
I Gaussiani punteggiati che circondano ogni bastone danno un’immagine più realistica di come dovrebbe essere lo spettro di assorbimento. In questo primo luogo ogni livello di energia (bastone) sarà dato una certa larghezza dal fatto che lo stato ha una vita finita. Tale ampliamento è chiamato ampliamento omogeneo poiché colpisce tutte le molecole nell’insieme in modo simile. C’è anche un allargamento a causa di piccole differenze nell’ambiente di ogni molecola. Questo tipo di ampliamento è chiamato ampliamento disomogeneo. Indipendentemente dall’origine il modello sopra è stato creato utilizzando un ampliamento gaussiano
Lo spostamento nucleare tra il terreno e lo stato eccitato determina la forma dello spettro di assorbimento. Esaminiamo sia uno spostamento di stato eccitato più piccolo che grande. Se \(S=½\) e le superfici di energia potenziale in questo caso sono:
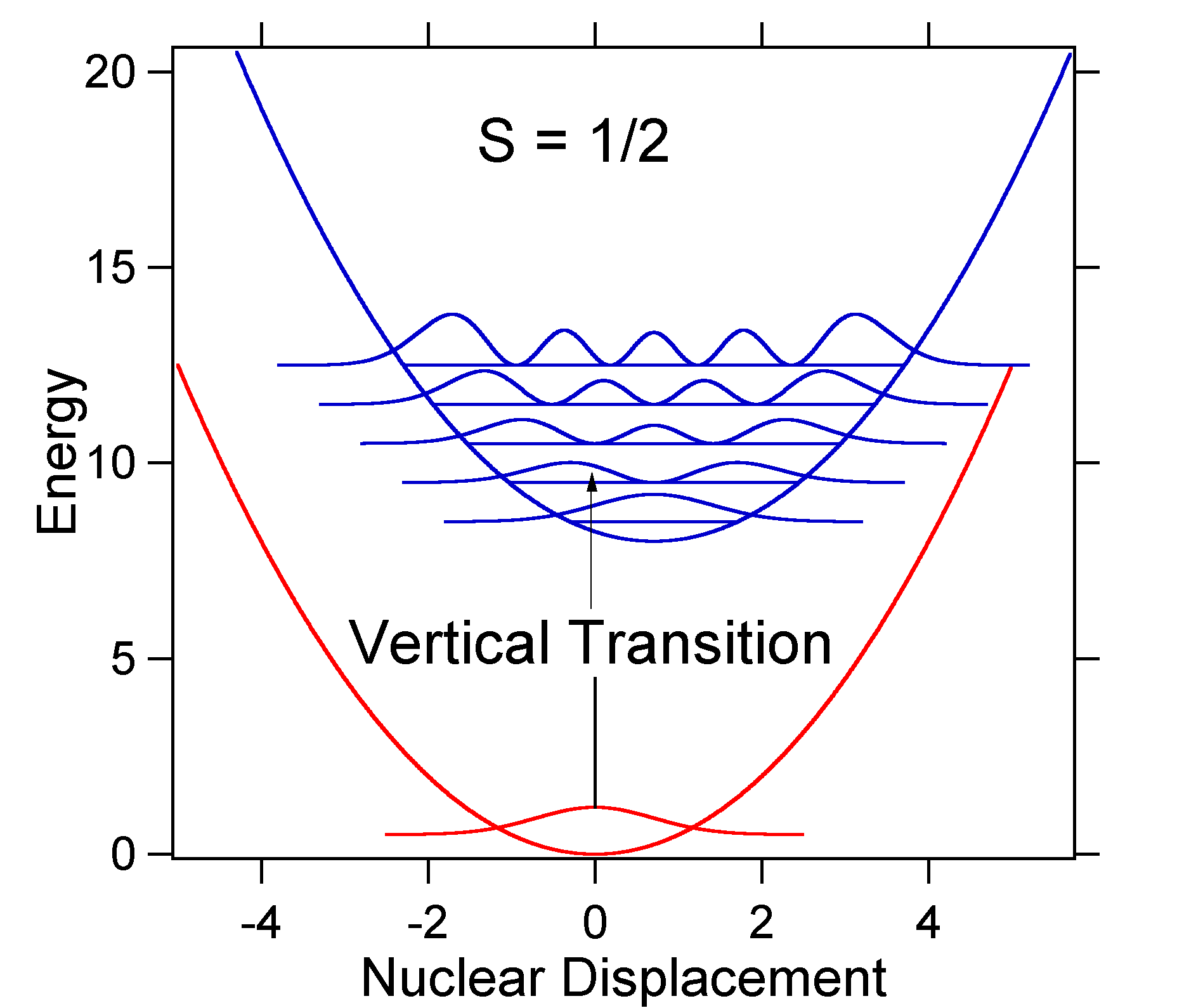
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
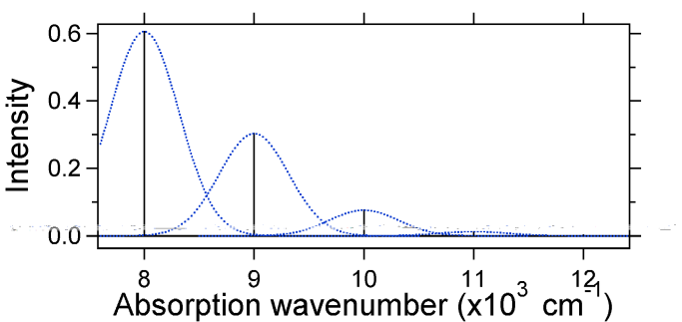
Si noti che la transizione vibrazionale zero-zero o \(S_{0,0}\) è molto grande nel caso in cui lo spostamento sia piccolo.
Come regola generale la costante \(S\) fornisce il rapporto tra l’intensità della transizione \(v = 2\) e la transizione \(v = 1\). In questo caso poiché \(S = 0.5\), la transizione \(v=2\) è 0.5 l’intensità della transizione \(v=1\).
Come esempio di uno spostamento maggiore la disposizione delle superfici di energia potenziale per S = 2 è mostrata sotto.
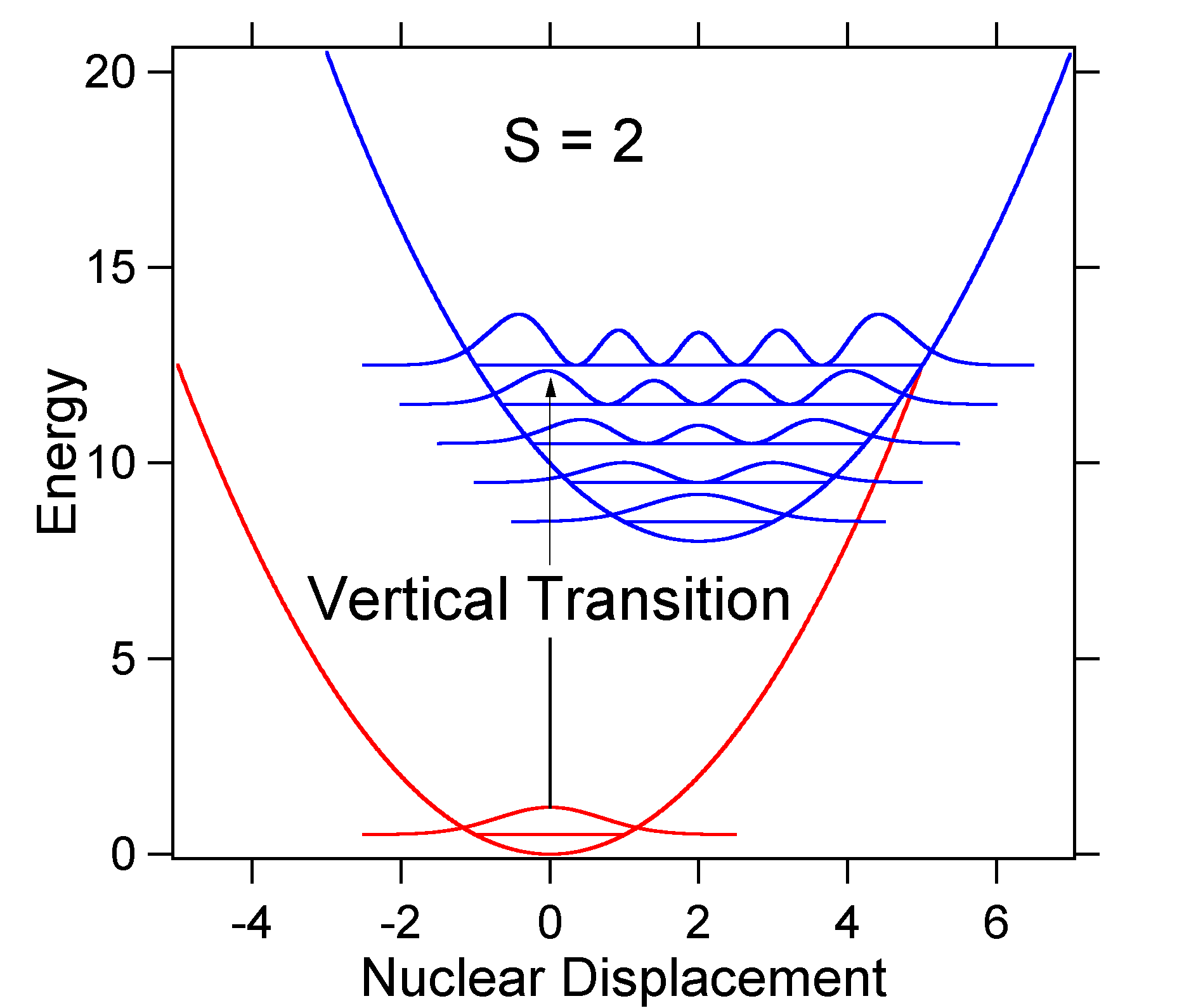
Lo spostamento maggiore comporta una diminuzione della sovrapposizione del livello dello stato fondamentale con il livello v = 0 dello stato eccitato. L’intensità massima sarà raggiunta in livelli vibrazionali più alti come mostrato nello spettro del bastone.
Gli spettri di assorbimento tracciati sotto hanno tutti la stessa intensità integrata, tuttavia le loro forme sono alterate a causa della diversa estensione dello spostamento della superficie energetica potenziale dello stato eccitato.
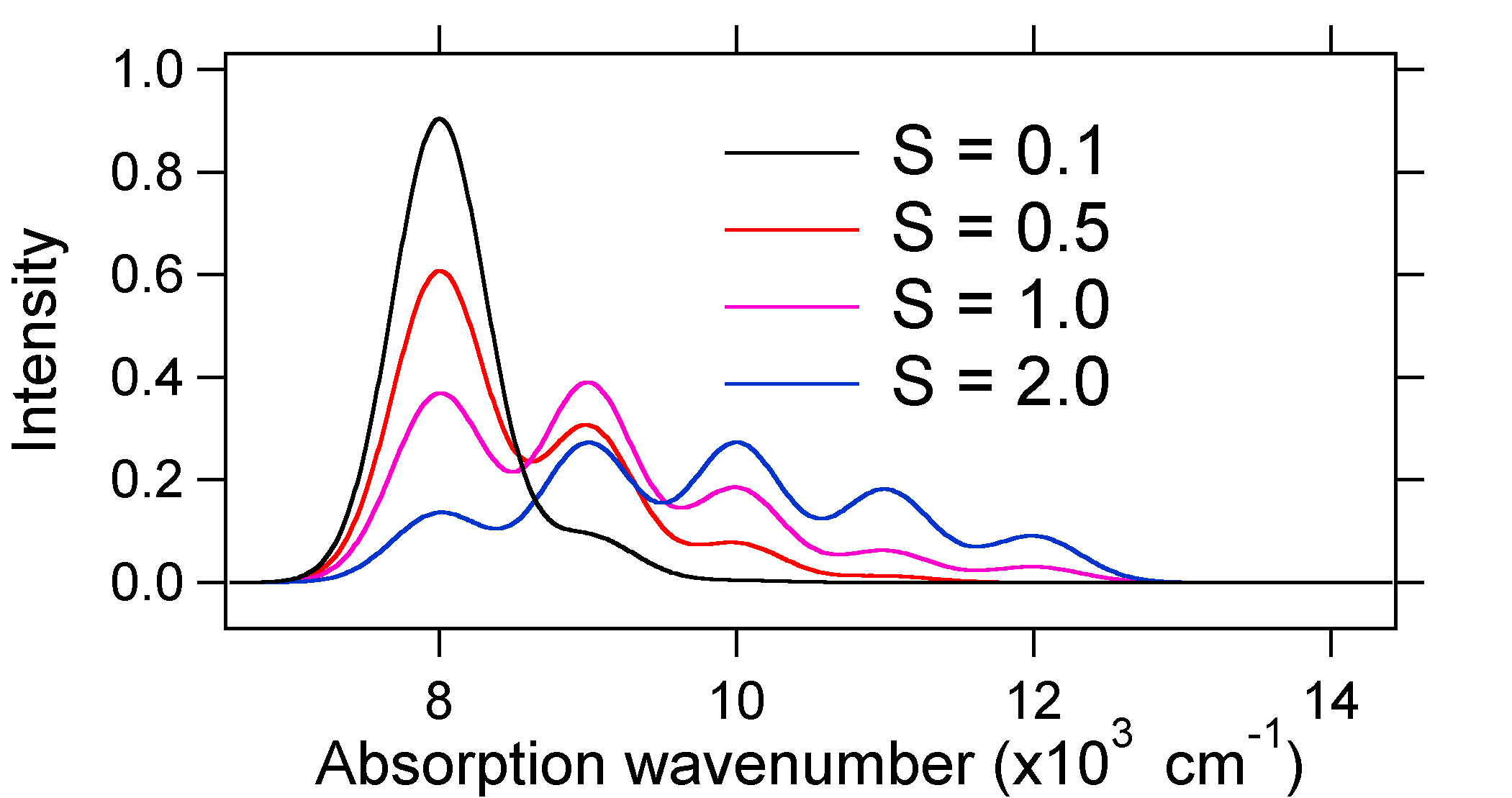
Quindi la natura delle intensità della banda vibronica relativa può dirci se c’è uno spostamento della coordinata nucleare di equilibrio che ha accompagnato una transizione. Quando ci sarà un aumento della lunghezza del legame (cioè, \ (Q_e > R_e\))? Ciò si verifica quando un elettrone viene promosso da un orbitale molecolare di legame a orbitali molecolari non leganti o anti-leganti (cioè quando l’ordine del legame è inferiore allo stato eccitato rispetto allo stato fondamentale).
- Non-legame orbitale molecolare \(\rightarrow\ legante orbitale molecolare
- Anti-incollaggio di orbitali molecolari \(\rightarrow\ legante orbitale molecolare
- Anti-incollaggio di orbitali molecolari \(\rightarrow\) non l’incollaggio di orbitale molecolare
In breve, quando il legame ordine è inferiore nello stato eccitato che in stato di terra, quindi \(Q_e > R_e\); un aumento bondlength si verifica quando questo accade.
- J. M. Luis, D. M. Bishop, B. Kirtman. Un approccio diverso per il calcolo dei fattori di Franck–Condon tra cui l’anarmonicità. J. Chem. Phys., 120 (2004), pp. 813-822.
- Atkins, Peter e Julio de Paula. Chimica fisica per le Scienze della vita. 2006. Il sito è stato pubblicato nel 2009. p. 563-564
- Principio di Franck-Condon. 1996, 68, 2243. IUPAC Compendio di Terminologia chimica 2a Edizione (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowitch e Govindjee. Assorbimento della luce e destino dell’eccitazione dell’energia. 1969. Principio di Franck-Condon. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contributors
- Matthew Ziering
-
Stefan Franzen (North Carolina State University)