Che cos’è un modello ARIMAX?

Qual è il modello ARIMAX?

Se hai letto la nostra serie di tutorial sul blog sui modelli per la stima dei dati delle serie temporali, hai già familiarità con 3 approcci principali: autoregressione, medie mobili e integrazione.

Qual è il tema comune in tutti questi modelli?

Si basavano esclusivamente su una singola variabile.

Tuttavia, un modello può anche prendere in considerazione più dei prezzi passati o dei residui passati.

E questi sono i cosiddetti modelli “MAX”, con l’ARMAX che è la versione non integrata e l’ARIMAX-il suo equivalente integrato.

Quindi, in questo tutorial, esploreremo come sono e ti mostreremo come implementarli in Python passo dopo passo.

Cominciamo, che ne dici?

Perché ARMAX e ARIMAX sono chiamati modelli “MAX”?

I nomi ARMAX e ARIMAX vengono come estensioni rispettivamente di ARMA e ARIMA. La X aggiunta alla fine sta per “esogeno”. In altre parole, suggerisce di aggiungere una variabile esterna diversa separata per aiutare a misurare la nostra variabile endogena.

L’equazione del modello ARMAX e ARIMAX:

Poiché l’unica differenza tra ARMAX e ARIMAX è che uno è integrato e l’altro no, possiamo esaminarne uno e quindi evidenziare come l’altro differirebbe.

Abbiamo esplorato un modello integrato nel nostro ultimo articolo del blog (ARIMA), quindi vediamo come appare l’equazione di ARIMAX.

ΔPt =c+ßX+ϕ1 ΔPt-1 + θ1 ϵt-1+ϵt

Naturalmente, l’equazione per l’ARMAX sarebbe la stessa, tranne che useremmo la variabile reale, diciamo P, invece del suo delta.

Pt=c+ßX+ϕ1 Pt-1+ θ1 ϵt-1 +ϵt

Scomponendo l’equazione di ARIMAX:

Possiamo pensare all’ARMAX come a un caso speciale dell’ARIMAX, dove l’ordine di integrazione è 0.

Quindi, per il resto del tutorial, ci concentreremo sull’ARIMAX.

E inizieremo scomponendo le diverse parti in esso. Per cominciare, Pt e Pt-1 rappresentano rispettivamente i valori nel periodo corrente e 1 periodo fa.

Allo stesso modo, ϵt e ϵt-1 sono i termini di errore per gli stessi due periodi. E, naturalmente, c è solo un fattore costante di base.

I due parametri, ϕ1 e θ1, esprimono quali parti del valore Pt-1 e l’errore ϵt-1 dell’ultimo periodo sono rilevanti nella stima di quello corrente.

Ora, le due nuove aggiunte al modello sono ” X ” e il suo coefficiente β. Proprio come ϕ, β è un coefficiente che sarà stimato in base alla selezione del modello e ai dati. Ma che dire di X?

Che cos’è una variabile esogena?

Bene, X è la variabile esogena e può essere qualsiasi variabile a cui siamo interessati.

Può essere una misurazione variabile nel tempo come il tasso di inflazione o il prezzo di un indice diverso. O una variabile categoriale che separa i diversi giorni della settimana. Può anche essere una contabilità booleana per i periodi festivi speciali. Infine, può rappresentare una combinazione di diversi fattori esterni.

L’idea è che possa essere qualsiasi altra variabile o variabile che possa influenzare i prezzi, purché abbiamo i dati disponibili.

Tali fattori esterni sono noti come variabili esogene nella nostra regressione. Usiamo i loro valori per prevedere e spiegare quello che ci interessa, che sembra essere prezzi correnti nel nostro caso.

Come implementare i modelli ARMAX e ARIMAX in Python?

Abbastanza convenientemente, il pacchetto statsmodels viene fornito con un metodo chiamato ARIMA che è pienamente in grado di gestire tali input aggiuntivi.

Iniziamo specificando le caratteristiche del modello e gli ordini del modello:

Dopo averlo fatto, dobbiamo anche specificare l’argomento esogeno chiamato “exog”.

Il valore che vogliamo passare deve essere un array di qualche tipo poiché desideriamo avere valori associati ad ogni periodo di tempo.

Ad esempio, possiamo usare S&P prezzi come questa variabile esogena, poiché li abbiamo già nei nostri dati.

Ora, siamo pronti per montare un modello ARIMAX (1,1,1).

Assicurati di nominare la variabile del modello in un modo che la distingua da modelli simili. In questo caso, scegliamo di farlo aggiungendo” X, spx”alla fine per indicare che la variabile esogena è S&P.

Quindi, come si può vedere dai frammenti, impostiamo questo uguale al metodo ARIMA come prima, aggiungiamo le serie temporali e l’ordine, come siamo abituati. Infine, tra i due, impostiamo l’argomento “exog” uguale a “DF SPX”, che indica i prezzi S&P.

Se adattiamo questo modello e stampiamo la sua tabella riassuntiva, vedremo che otteniamo una riga aggiuntiva per i prezzi S & P.

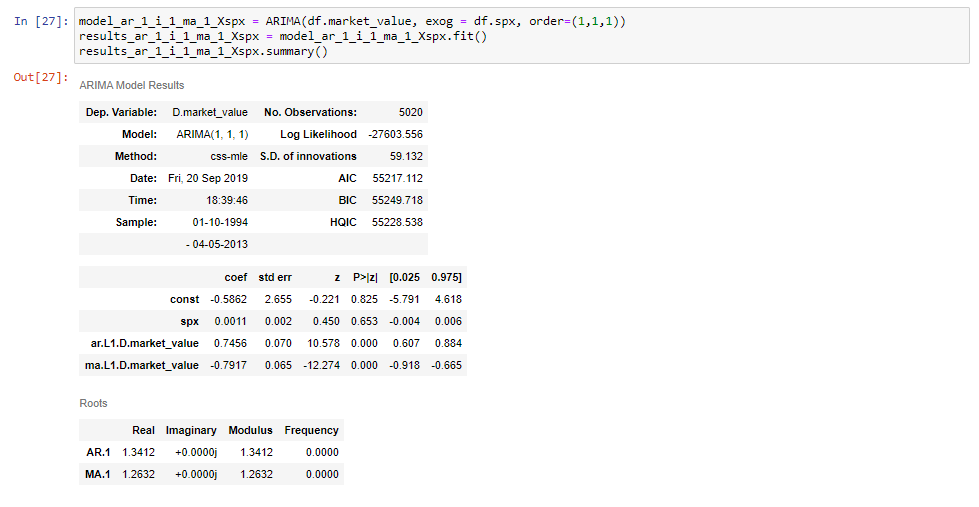
E questo è tutto quello che c’è da fare!

Abbiamo visto con successo come implementare un modello ARIMAX in Python.

Se vuoi saperne di più su ARIMAX e altri modelli di serie temporali in Python, assicurati di controllare i nostri tutorial passo-passo su Python. Se sei nuovo in Python e sei entusiasta di saperne di più, questo articolo completo sull’apprendimento della programmazione Python ti guiderà dall’installazione, attraverso IDE Python, librerie e framework, ai migliori percorsi di carriera Python e prospettive di lavoro.

Pronto a fare il prossimo passo verso una carriera nella scienza dei dati?

Scopri il programma completo di scienza dei dati oggi. Inizia con i fondamenti con i nostri corsi di statistica, matematica ed Excel. Crea un’esperienza passo-passo con SQL, Python, R, Power BI e Tableau. E migliora il tuo skillset con Machine Learning, Deep Learning, modellazione del rischio di credito, analisi delle serie temporali e analisi dei clienti in Python. Non sei ancora sicuro di voler trasformare il tuo interesse per la scienza dei dati in una carriera? Puoi esplorare il curriculum o iscriverti gratuitamente a 15 ore di contenuti video da principiante a avanzato facendo clic sul pulsante qui sotto.