
Una Rete Neurale Artificiale (ANN) è fatto di molti neuroni interconnessi:
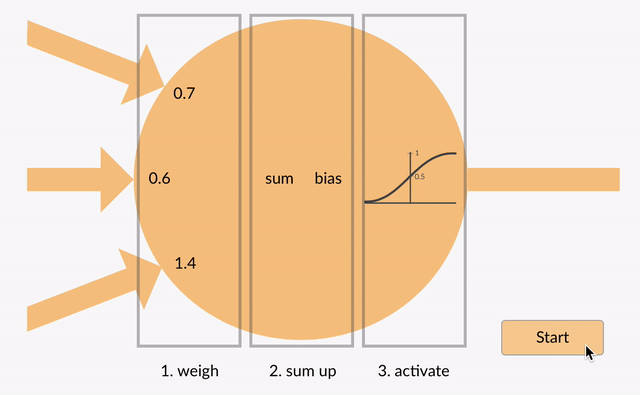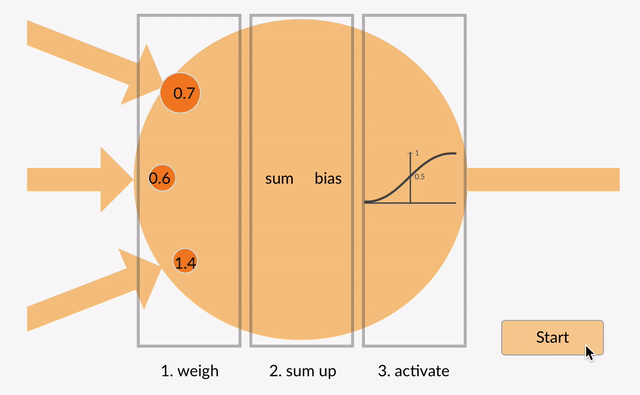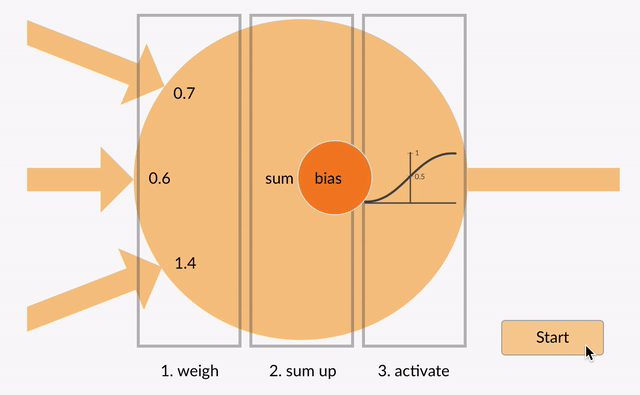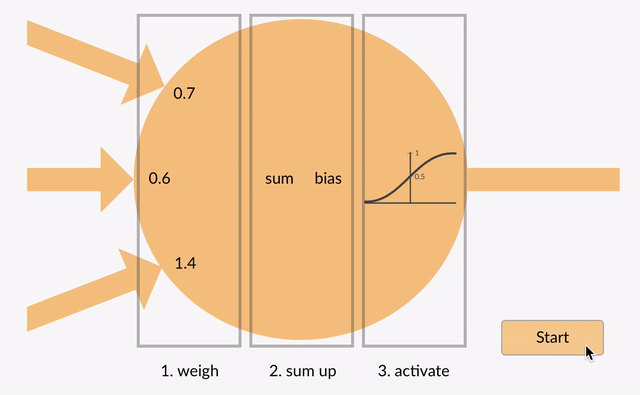
Ogni neurone prende in alcuni numeri in virgola mobile (ad esempio, 1.0, 0.5, -1.0) e li moltiplica per alcuni altri numeri in virgola mobile (ad esempio 0.7, 0.6, 1.4) noti come pesi (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). I pesi agiscono come un meccanismo per concentrarsi su, o ignorare, determinati input.

ponderato di ingressi quindi ottenere sommati insieme (ad es. 0.7 + 0.3 + -1.4 = -0.4) insieme a un valore di bias (ad esempio -0.4 + -0.1 = -0.5).
Il valore sommato (x) viene ora trasformato in un valore di output (y) in base alla funzione di attivazione del neurone (y = f(x)). Alcuni popolari funzioni di attivazione sono illustrati di seguito:

ad esempio, -0.5 → -0.05 se usiamo la Perde Rettificato Unità Lineare (che Perde ReLU) attivazione della funzione: y = f(x) = f(-0.5) = max(0.1*-0.5, -0.5) = max(-0.05, -0.5) = -0.05
Il valore di output del neurone (ad esempio -0.05) è spesso un input per un altro neurone.
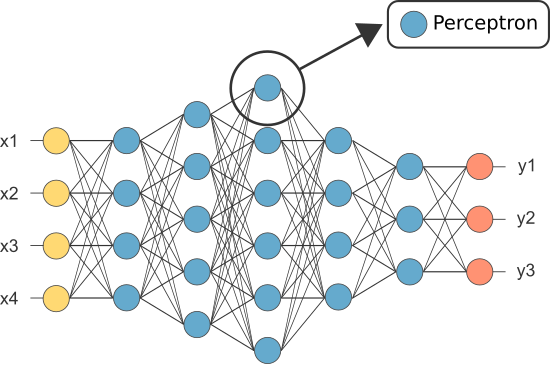
Tuttavia, uno dei primi Ann era conosciuto come il perceptron e consisteva solo di un singolo neurone.

L’output del (solo) neurone del perceptron funge da previsione finale.

Lascia codice nostri Perceptron:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Nota: non abbiamo incluso algoritmo di apprendimento nell’esempio di cui sopra — dobbiamo coprire algoritmi di apprendimento in un altro tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

Quindi perché abbiamo bisogno di così tanti neuroni in un ANN se uno sarà sufficiente (come classificatore)?

Sfortunatamente, i singoli neuroni sono solo in grado di classificare i dati separabili linearmente.

Tuttavia, combinando i neuroni insieme, essenzialmente combiniamo i loro limiti decisionali. Pertanto, un ANN composto da molti neuroni è in grado di apprendere confini decisionali complessi e non lineari.

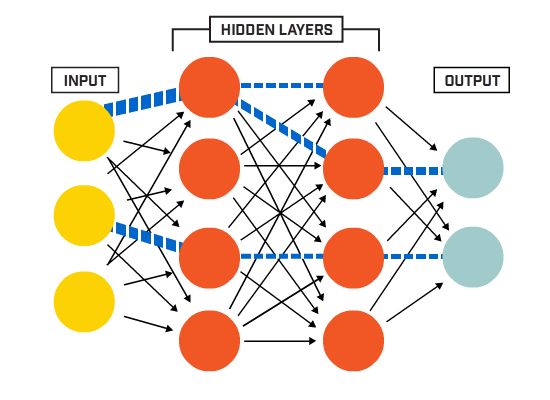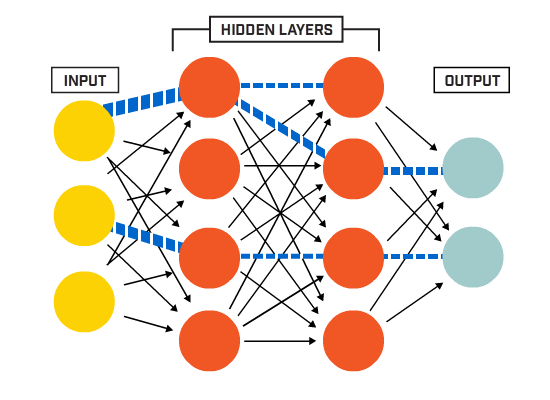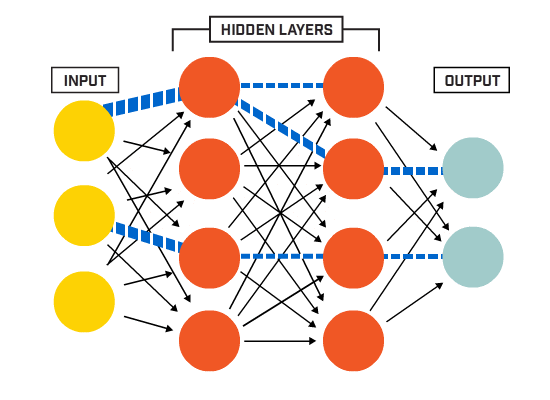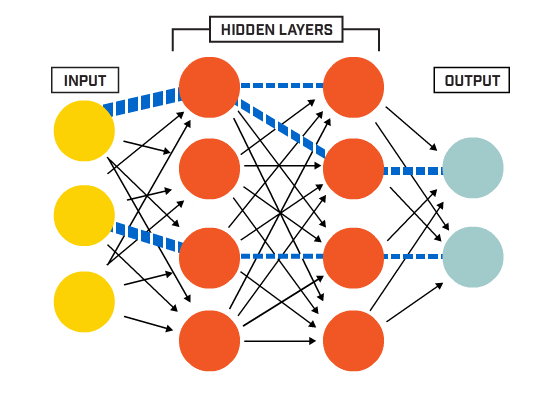
I neuroni sono collegati tra loro secondo una specifica architettura di rete. Sebbene ci siano architetture diverse, quasi tutte contengono livelli. (NB: Neuroni nello stesso livello non collegare uno con l’altro)
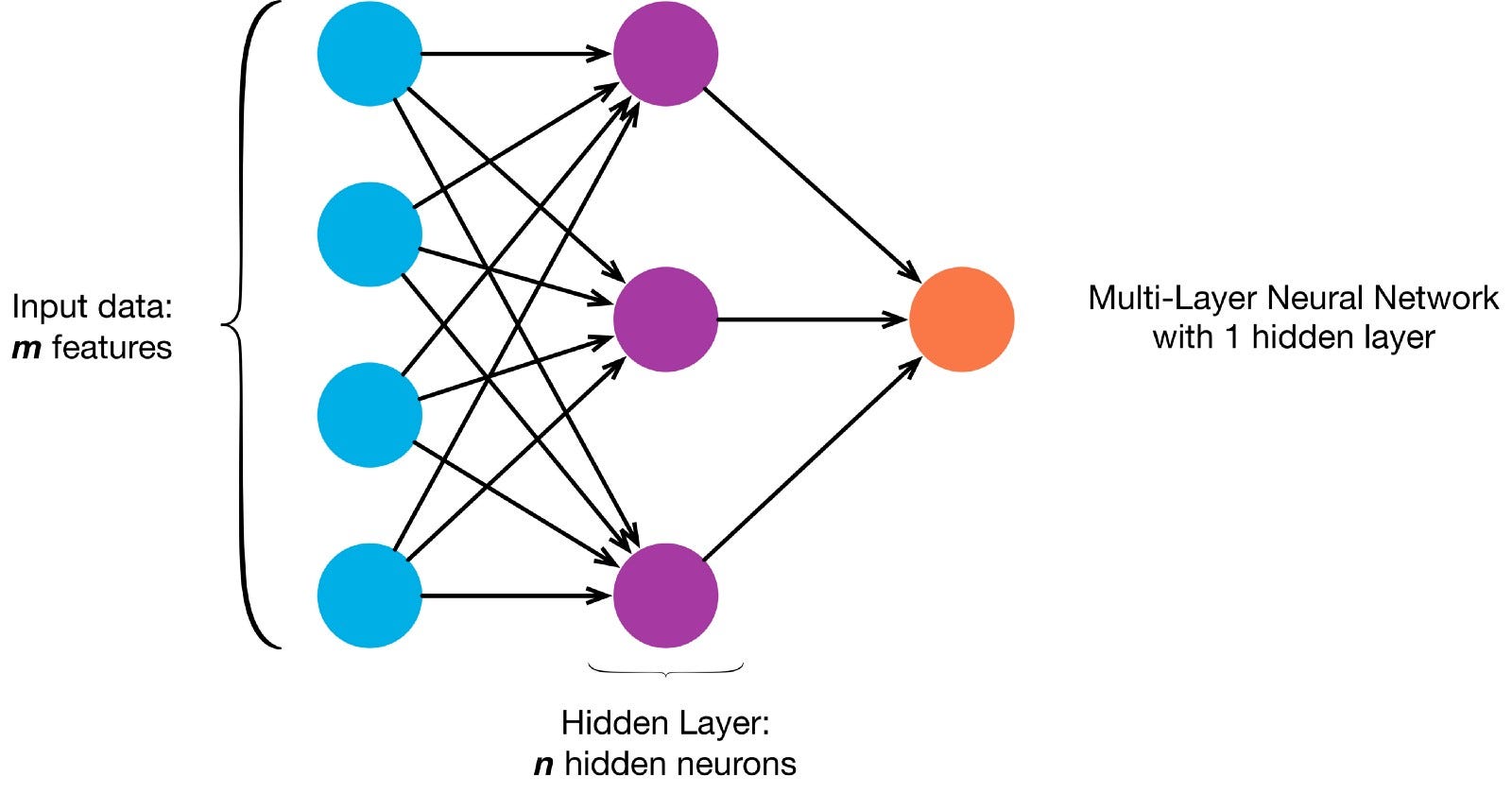
non C’è in genere un livello di input (contenente un numero di neuroni pari al numero di funzioni di immissione dati), un livello di output (contenente un numero di neuroni pari al numero delle classi) e uno strato nascosto (contenente un qualsiasi numero di neuroni).

Ci possono essere più di uno strato nascosto per permettere la rete neurale per saperne di più complesso decisione confini (Qualsiasi rete neurale con più di uno strato nascosto è considerato un profondo rete neurale).
Consente di creare un NN profondo per dipingere questa immagine:

Permette di scaricare l’immagine e carica i pixel in un array
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
insegnare ai nostri ANN a dipingere è un apprendimento supervisionato compito, quindi, abbiamo bisogno di creare un etichettati training set (la Nostra formazione dati di input e output previsto etichette per ogni ingresso). Gli input di allenamento avranno 2 valori (le coordinate x,y di ciascun pixel).
Data la semplicità dell’immagine, potremmo effettivamente affrontare questo problema in due modi. Un problema di classificazione (in cui la rete neurale predice se un pixel appartiene alla classe “blu” o alla classe “grigia”, date le sue coordinate xy) o un problema di regressione (in cui la rete neurale predice i valori RGB per un pixel date le sue coordinate).
Se si tratta di un problema di regressione: gli output di allenamento avranno 3 valori (i valori r,g,b normalizzati per ciascun pixel). – Consente di utilizzare questo metodo per ora.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Ora consente di creare il nostro ANN:

- Si dovrebbe avere 2 neuroni del livello di input (dato che ci sono 2 valori di prendere in: x & y coordinate).
- Dovrebbe avere 3 neuroni nel livello di output (poiché ci sono 3 valori da imparare: r, g, b).
- numero di livelli nascosti e il numero di neuroni in ogni livello nascosto sono due hyperparameters di sperimentare (così come il numero di epoche ci si allena per la funzione di attivazione, ecc) — io uso 10 livelli nascosti con 100 neuroni in ogni strato nascosto (rendendo questo un deep neural network)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
La rete addestrata può oggi prevedere normalizzato i valori rgb per ogni coordinate (ad esempio x,y = 1,1).
ann.predict(])
array(])
consente di utilizzare l’ANN per predire i valori rgb per ogni coordinata e permette di visualizzare il predetto valori rgb per l’intera immagine per vedere quanto bene ha fatto (qualitativamente — partiremo metriche di valutazione per un altro tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Provare a cambiare il hyperparameters per ottenere risultati migliori.
Se invece di trattare questo come un problema di regressione, abbiamo trattare questo come un problema di classificazione, quindi la formazione uscite di 2 valori (la probabilità di pixel appartenenti ad ognuna delle due classi: “blu” e “grigie”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
Siamo in grado di ricostruire il nostro ANN come un classificatore binario con 2 neuroni del livello di input, 2 neuroni nello strato di output e 100 neuroni in strato nascosto (con 10 livelli nascosti)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
E ‘ ora possibile utilizzare i formati ANN per predire la classe che ogni pixel appartiene (0: “grigio” o 1: “blu”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

