
L’apprendimento automatico viene utilizzato in ultima analisi per prevedere i risultati con una serie di funzionalità. Pertanto, tutto ciò che possiamo fare per generalizzare le prestazioni del nostro modello è visto come un guadagno netto. Dropout è una tecnica utilizzata per impedire a un modello di overfitting. Dropout funziona impostando casualmente i bordi in uscita delle unità nascoste (neuroni che compongono i livelli nascosti) a 0 ad ogni aggiornamento della fase di allenamento. Se dai un’occhiata alla documentazione di Keras per il livello dropout, vedrai un link a un white paper scritto da Geoffrey Hinton e amici, che approfondisce la teoria alla base del dropout.
Nell’esempio in corso, useremo Keras per costruire una rete neurale con l’obiettivo di riconoscere le cifre scritte a mano.
from keras.datasets import mnist
from matplotlib import pyplot as plt
plt.style.use('dark_background')
from keras.models import Sequential
from keras.layers import Dense, Flatten, Activation, Dropout
from keras.utils import normalize, to_categorical
Usiamo Keras per importare i dati nel nostro programma. I dati sono già suddivisi nei set di allenamento e test.
(X_train, y_train), (X_test, y_test) = mnist.load_data()
Diamo un’occhiata per vedere con cosa stiamo lavorando.
plt.imshow(x_train, cmap = plt.cm.binary)
plt.show()

Dopo che abbiamo finito l’allenamento fuori modello, dovrebbe essere in grado di riconoscere la precedente immagine di cinque.
C’è un po ‘ di pre-elaborazione che dobbiamo eseguire in anticipo. Normalizziamo i pixel (caratteristiche) in modo tale che vadano da 0 a 1. Ciò consentirà al modello di convergere verso una soluzione molto più veloce. Successivamente, trasformiamo ciascuna delle etichette di destinazione per un dato campione in una matrice di 1 e 0 in cui l’indice del numero 1 indica la cifra rappresentata dall’immagine. Lo facciamo perché altrimenti il nostro modello interpreterebbe la cifra 9 come avente una priorità più alta del numero 3.
X_train = normalize(X_train, axis=1)
X_test = normalize(X_test, axis=1)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
Senza Dropout
Prima di alimentare una matrice 2 dimensionale in una rete neurale, usiamo uno strato appiattito che lo trasforma in un array 1 dimensionale aggiungendo ogni riga successiva a quella che l’ha preceduta. Useremo due strati nascosti composti da 128 neuroni ciascuno e uno strato di output composto da 10 neuroni, ciascuno per una delle 10 cifre possibili. La funzione di attivazione softmax restituirà la probabilità che un campione rappresenti una data cifra.

Dal momento che stiamo cercando di prevedere le classi, usiamo categorico crossentropy come la perdita di funzione. Misureremo le prestazioni del modello utilizzando la precisione.
model.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
Abbiamo messo da parte il 10% dei dati per la convalida. Useremo questo per confrontare la tendenza di un modello di overfit con e senza dropout. Una dimensione del lotto di 32 implica che calcoleremo il gradiente e faremo un passo nella direzione del gradiente con una grandezza uguale al tasso di apprendimento, dopo aver passato 32 campioni attraverso la rete neurale. Lo facciamo un totale di 10 volte come specificato dal numero di epoche.
history = model.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Siamo in grado di tracciare la formazione e la validazione precisione in ogni epoca, utilizzando la cronologia variabile restituita dalla funzione di adattamento.
Come puoi vedere, senza dropout, la perdita di convalida smette di diminuire dopo la terza epoca.

As you can see, without dropout, the validation accuracy tends to plateau around the third epoch.

Using this simple model, we still managed to obtain an accuracy of over 97%.
test_loss, test_acc = model.evaluate(X_test, y_test)
test_acc
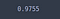
di Filtraggio
C’è un certo dibattito se il forcellino deve essere inserito prima o dopo l’attivazione della funzione. Come regola generale, posizionare il dropout dopo la funzione attiva per tutte le funzioni di attivazione diverse da relu. Passando 0.5, ogni unità nascosta (neurone) è impostata su 0 con una probabilità di 0.5. In altre parole, c’è un cambiamento del 50% che l’output di un dato neurone sarà costretto a 0.

di Nuovo, dal momento che stiamo cercando di prevedere le classi, usiamo categorico crossentropy come la perdita di funzione.
model_dropout.compile(
loss='categorical_crossentropy',
optimizer='adam',
metrics=
)
Fornendo il parametro split validations, il modello separerà una frazione dei dati di allenamento e valuterà la perdita e qualsiasi metrica del modello su questi dati alla fine di ogni epoca. Se la premessa dietro dropout tiene, allora dovremmo vedere una notevole differenza nella precisione di convalida rispetto al modello precedente. Il parametro shuffle mescolerà i dati di allenamento prima di ogni epoca.
history_dropout = model_dropout.fit(
X_train,
y_train,
epochs=10,
batch_size=32,
validation_split=0.1,
verbose = 1,
shuffle=True
)

Come si può vedere, la validazione, la perdita è significativamente inferiore rispetto a quella ottenuta utilizzando il modello regolare.

Come si può vedere, il modello convergente molto più veloce e ottenuto una precisione vicina al 98% sul set di convalida, mentre il precedente modello stabilizzato intorno al terzo epoca.

La precisione ottenuta sul set di testing non è molto diversa da quella ottenuta dal modello senza filtraggio. Ciò è probabilmente dovuto al numero limitato di campioni.
test_loss, test_acc = model_dropout.evaluate(X_test, y_test)
test_acc

conclusioni
Filtraggio può aiutare un modello di generalizzare in modo casuale impostando l’uscita per un dato neurone a 0. Impostando l’output su 0, la funzione di costo diventa più sensibile ai neuroni vicini cambiando il modo in cui i pesi verranno aggiornati durante il processo di backpropagation.