Introduzione alla stima del movimento con flusso ottico

In questo tutorial, ci immergiamo nei fondamenti del flusso ottico, guardiamo alcune delle sue applicazioni e implementiamo le sue due varianti principali (sparse e dense). Discutiamo anche brevemente approcci più recenti che utilizzano l’apprendimento profondo e promettenti direzioni future.

Recenti scoperte nella ricerca sulla visione artificiale hanno permesso alle macchine di percepire il mondo circostante attraverso tecniche come il rilevamento di oggetti per rilevare istanze di oggetti appartenenti a una certa classe e la segmentazione semantica per la classificazione in pixel.

Tuttavia, per l’elaborazione di input video in tempo reale, la maggior parte delle implementazioni di queste tecniche indirizzano solo le relazioni di oggetti all’interno dello stesso frame \((x, y)\) ignorando le informazioni temporali \((t)\). In altre parole, rivalutano ogni fotogramma in modo indipendente, come se fossero immagini completamente non correlate, per ogni esecuzione. Tuttavia, cosa succede se abbiamo bisogno delle relazioni tra fotogrammi consecutivi, ad esempio, vogliamo tracciare il movimento dei veicoli attraverso i fotogrammi per stimare la sua velocità attuale e prevedere la sua posizione nel fotogramma successivo?

O, in alternativa, cosa succede se richiediamo informazioni sulle relazioni di posa umane tra fotogrammi consecutivi per riconoscere azioni umane come tiro con l’arco, baseball e basket?

In questo tutorial, impariamo che il Flusso Ottico è, come implementare le sue due varianti principali (sparse e denso), e anche ottenere un grande quadro dei più recenti approcci che coinvolgono apprendimento profondo e promettenti direzioni future.

Che cos’è il flusso ottico?
Implementazione del flusso ottico sparso
Implementazione del flusso ottico denso
Deep learning and beyond

Cos’è il flusso ottico?

Iniziamo con una comprensione di alto livello del flusso ottico. Il flusso ottico è il movimento di oggetti tra fotogrammi consecutivi di sequenza, causato dal movimento relativo tra l’oggetto e la fotocamera. Il problema del flusso ottico può essere espresso come:

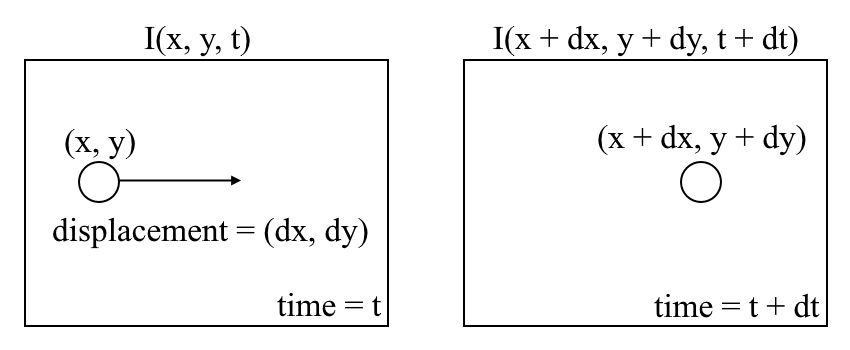
dove tra fotogrammi consecutivi, possiamo esprimere l’intensità dell’immagine \((I)\) in funzione dello spazio \((x, y)\) e tempo \((t)\). In altre parole, se prendiamo la prima immagine \(I(x, y, t)\) e spostiamo i suoi pixel di \((dx, dy)\) sul tempo \(t\), otteniamo la nuova immagine \(I(x + dx, y + dy, t + dt)\).

In primo luogo, assumiamo che le intensità dei pixel di un oggetto siano costanti tra fotogrammi consecutivi.

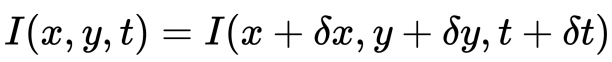
In secondo luogo, prendiamo l’approssimazione della serie di Taylor dell’RHS e rimuoviamo i termini comuni.

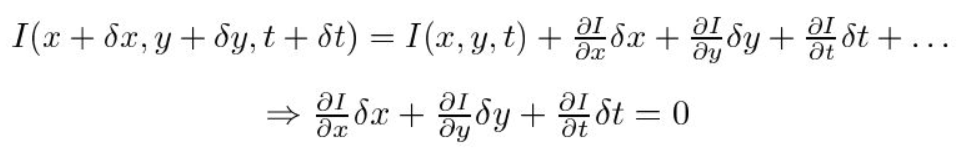
In terzo luogo, dividiamo per \(dt\) per ricavare l’equazione del flusso ottico:

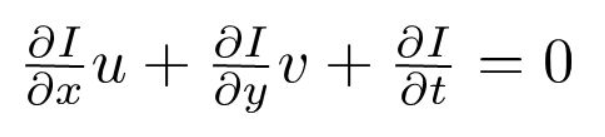
dove \(u = dx/dt\) e \(v = dy/dt\).

\(DI/dx, DI/dy\) e \(DI/dt\) sono i gradienti dell’immagine lungo l’asse orizzontale, l’asse verticale e il tempo. Quindi, concludiamo con il problema del flusso ottico, cioè risolvendo \(u(dx/dt)\) e \(v (dy/dt)\) per determinare il movimento nel tempo. Potresti notare che non possiamo risolvere direttamente l’equazione del flusso ottico per \(u\) e \(v\) poiché esiste una sola equazione per due variabili sconosciute. Implementeremo alcuni metodi come il metodo Lucas-Kanade per risolvere questo problema.

Flusso ottico sparso vs denso

Il flusso ottico sparso fornisce i vettori di flusso di alcune “caratteristiche interessanti” (ad esempio pochi pixel che raffigurano i bordi o gli angoli di un oggetto) all’interno del fotogramma mentre il flusso ottico denso, che fornisce i vettori di flusso dell’intero fotogramma (tutti i pixel) – fino a un vettore di Come avresti intuito, il flusso ottico denso ha una maggiore precisione al costo di essere lento / computazionalmente costoso.

Implementazione del flusso ottico sparso

Il flusso ottico sparso seleziona un set di pixel sparso (ad esempio caratteristiche interessanti come bordi e angoli) per tracciare i suoi vettori di velocità (movimento). Le funzioni estratte vengono passate nella funzione flusso ottico da fotogramma a fotogramma per garantire che gli stessi punti vengano tracciati. Ci sono varie implementazioni di flusso ottico sparse, tra cui il metodo Lucas–Kanade, il metodo Horn–Schunck, il metodo Buxton–Buxton, e altro ancora. Useremo il metodo Lucas-Kanade con OpenCV, una libreria open source di algoritmi di visione artificiale, per l’implementazione.

Impostazione ambiente

Se non si dispone già di OpenCV installato, aprire il Terminale ed eseguire:

pip install opencv-python

Ora, clonare il tutorial repository mediante l’esecuzione di:

git clone https://github.com/chuanenlin/optical-flow.git

Avanti, aperto sparse-starter.py con il vostro editor di testo. Scriveremo tutto il codice in questo file Python.

Configurazione di OpenCV per leggere un video e impostazione dei parametri

Shi-Tomasi Corner Detector – selezione dei pixel da tracciare

Per l’implementazione di un flusso ottico sparso, tracciamo solo il movimento di un set di funzionalità di pixel. Le caratteristiche delle immagini sono punti di interesse che presentano informazioni ricche di contenuti dell’immagine. Ad esempio, tali caratteristiche possono essere punti nell’immagine che sono invarianti alla traslazione, scala, rotazione e variazioni di intensità come gli angoli.

Il rilevatore di angoli Shi-Tomasi è molto simile al popolare rilevatore di angoli Harris che può essere implementato con le seguenti tre procedure:

1. Determinare finestre (piccole patch di immagini) con grandi gradienti (variazioni di intensità dell’immagine) quando tradotto in entrambe le direzioni \(x\) e \(y\).
2. Per ogni finestra, calcola un punteggio \(R\).
3. A seconda del valore di \(R\), ogni finestra è classificata come piatta, bordo o angolo.

Se volete saperne di più su una spiegazione matematica passo-passo del rivelatore angolo Harris, sentitevi liberi di passare attraverso queste diapositive.

Shi e Tomasi in seguito apportarono una piccola ma efficace modifica al rilevatore di angoli Harris nelle loro buone caratteristiche di carta da tracciare.

La modifica riguarda l’equazione in cui viene calcolato il punteggio \(R\). Nel rivelatore angolo Harris, la funzione di punteggio è data da:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

Invece, Shi-Tomasi proposto la funzione di punteggio, come:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

il che significa in pratica che se \(R\) è maggiore di una soglia, esso è classificato come un angolo. Quanto segue confronta le funzioni di punteggio di Harris (a sinistra) e Shi-Tomasi(a destra) nello spazio \(λ1-λ2\).

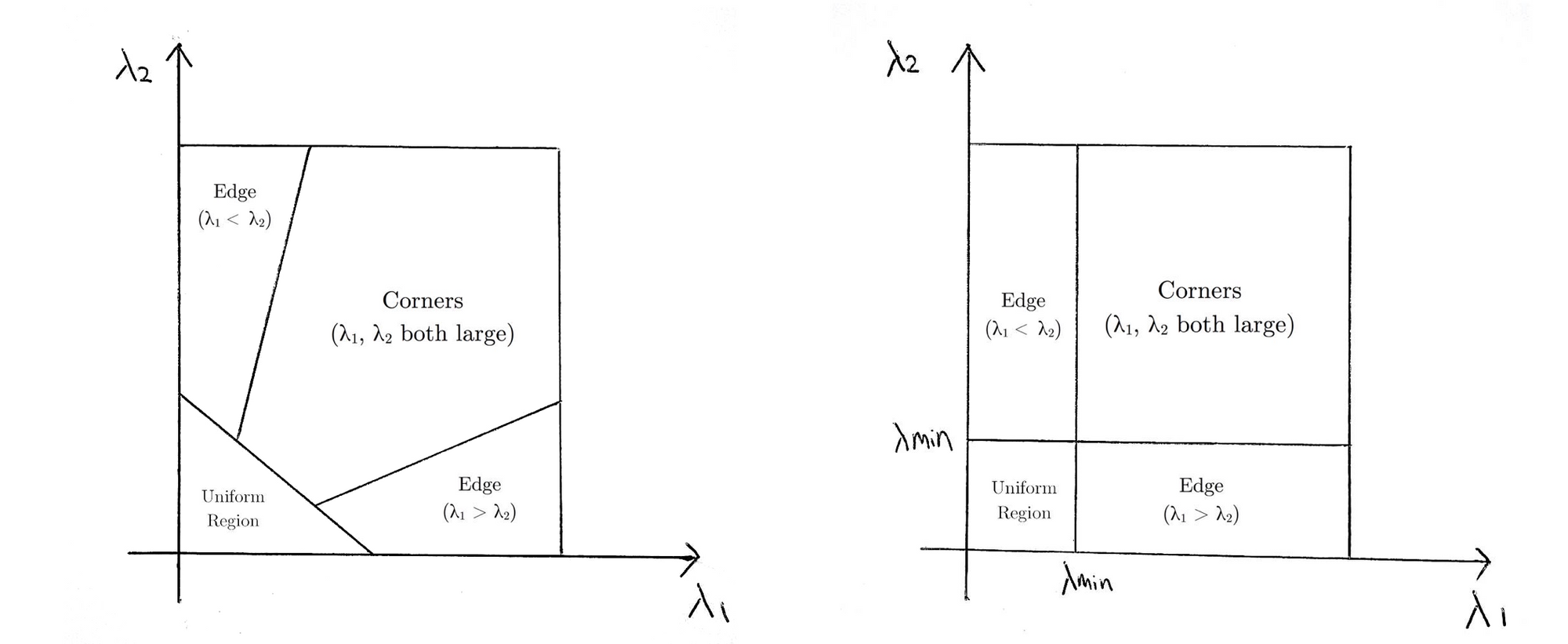
Per Shi-Tomasi, solo quando \(λ1\) e \(λ2\) sono al di sopra di una soglia minima \(λmin\) la finestra è classificata come angolo.

La documentazione dell’implementazione di OpenCV di Shi-Tomasi tramite goodFeaturesToTrack() può essere trovata qui.

Tracciamento di oggetti specifici

Potrebbero esserci scenari in cui si desidera tracciare solo un oggetto specifico di interesse (ad esempio il tracciamento di una determinata persona) o una categoria di oggetti (come tutti i veicoli a 2 ruote nel traffico). È possibile modificare facilmente il codice per tracciare i pixel degli oggetti desiderati modificando la variabileprev.

È anche possibile combinare il rilevamento di oggetti con questo metodo per stimare solo il flusso di pixel all’interno dei riquadri di delimitazione rilevati. In questo modo è possibile tenere traccia di tutti gli oggetti di un particolare tipo/categoria nel video.

Lucas-Kanade: Sparse Optical Flow

Lucas e Kanade hanno proposto una tecnica efficace per stimare il movimento di caratteristiche interessanti confrontando due fotogrammi consecutivi nella loro carta Una tecnica di registrazione dell’immagine iterativa con un’applicazione alla visione stereo. Il metodo Lucas-Kanade funziona secondo le seguenti ipotesi:

1. Due fotogrammi consecutivi sono separati da un piccolo incremento temporale (\(dt\)) in modo tale che gli oggetti non vengano spostati in modo significativo (in altre parole, il metodo funziona meglio con oggetti in movimento lento).
2. Una cornice ritrae una scena “naturale” con oggetti testurizzati che mostrano sfumature di grigio che cambiano senza intoppi.

In primo luogo, sotto queste ipotesi, possiamo prendere una piccola finestra 3×3 (quartiere) intorno alle caratteristiche rilevate da Shi-Tomasi e supporre che tutti e nove i punti abbiano lo stesso movimento.

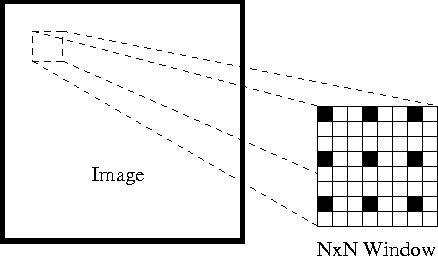
Questo può essere rappresentato come

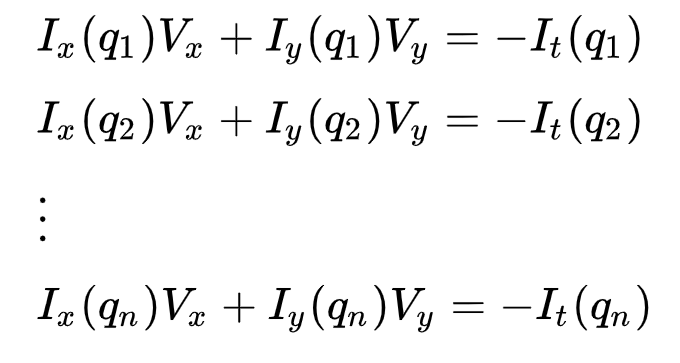
dove \(q_1, q_2, …, q_n\) indicare i pixel all’interno della finestra (ad esempio \(n\) = 9 per un 3×3 finestra) e \(I_x(q_i)\), \(I_y(q_i)\) e \(I_t(q_i)\) indicano le derivate parziali di immagine \(I\) rispetto alla posizione di \((x, y)\) e di \(t\), per il pixel \(q_i\) al momento attuale.

Questa è solo l’equazione del flusso ottico (che abbiamo descritto in precedenza) per ciascuno degli n pixel.

Il set di equazioni può essere rappresentato nella seguente forma matriciale in cui \(Av = b\):

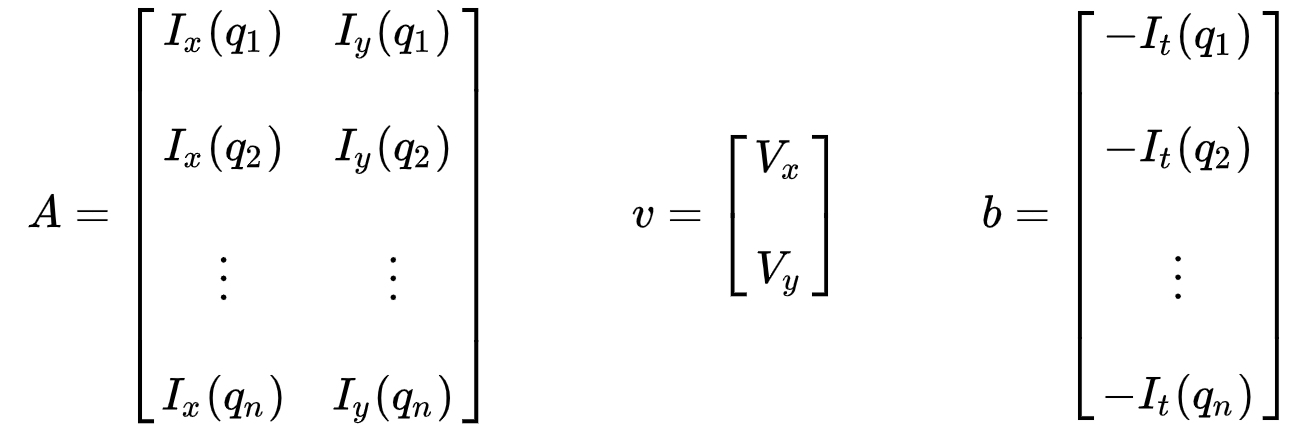
Prendere nota che in precedenza (vedi “che Cosa è il flusso ottico?”sezione), abbiamo affrontato il problema di dover risolvere per due variabili sconosciute con una sola equazione. Ora ci troviamo di fronte a dover risolvere per due incognite (\(V_x\) e \(V_y\)) con nove equazioni, che è troppo determinato.

in Secondo luogo, per affrontare l’eccessiva determinato problema, si applica minimi quadrati per ottenere le seguenti due equazioni a due sconosciuti problema:

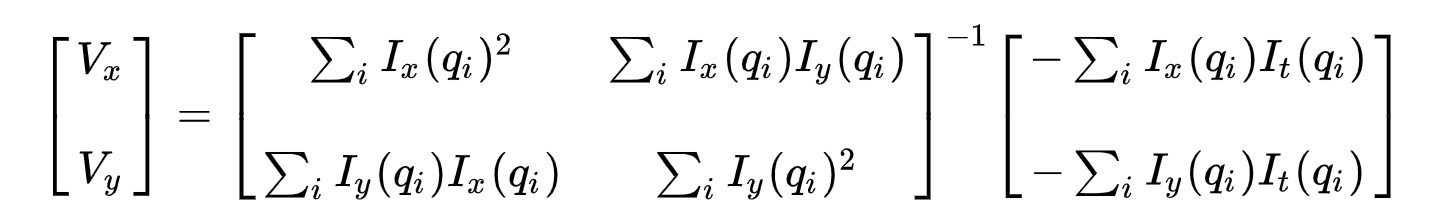
dove \(Vx = u = dx/dt\) indica il movimento di \(x\) in funzione del tempo e \(Vy = v = dy/dt\) indica il movimento di y nel corso del tempo. Risolvere per le due variabili completa il problema del flusso ottico.

In poche parole, identifichiamo alcune caratteristiche interessanti per tracciare e calcolare iterativamente i vettori di flusso ottico di questi punti. Tuttavia, l’adozione del metodo Lucas-Kanade funziona solo per piccoli movimenti (dalla nostra ipotesi iniziale) e fallisce quando c’è un grande movimento. Pertanto, l’implementazione OpenCV del metodo Lucas-Kanade adotta piramidi.

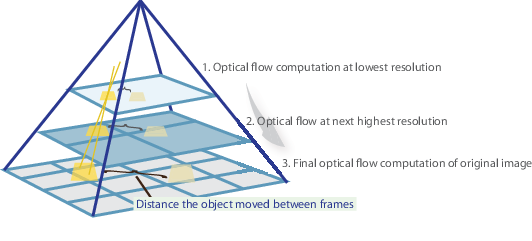
In una vista di alto livello, i piccoli movimenti vengono trascurati mentre saliamo sulla piramide e i grandi movimenti vengono ridotti a piccoli movimenti-calcoliamo il flusso ottico insieme alla scala. Una spiegazione matematica completa dell’implementazione di OpenCV può essere trovata nelle note di Bouguet e la documentazione dell’implementazione di OpenCV del metodo Lucas-Kanade tramite calcOpticalFlowPyrLK() può essere trovata qui.

Visualizzando

E il gioco è fatto! Aprire il terminale ed eseguire

python sparse-starter.py

per testare l’implementazione del flusso ottico sparso. 👏

Nel caso in cui hai perso qualsiasi codice, il codice completo può essere trovato in sparse-solution.py.

Implementazione del flusso ottico denso

Abbiamo precedentemente calcolato il flusso ottico per un set di funzionalità sparse di pixel. Il flusso ottico denso tenta di calcolare il vettore di flusso ottico per ogni pixel di ciascun fotogramma. Mentre tale calcolo può essere più lento, dà un risultato più accurato e un risultato più denso adatto per applicazioni come la struttura di apprendimento dal movimento e la segmentazione video. Esistono varie implementazioni di flusso ottico denso. Useremo il metodo Farneback, una delle implementazioni più popolari, con l’utilizzo di OpenCV, una libreria open source di algoritmi di visione artificiale, per l’implementazione.

Impostazione dell’ambiente

Se non lo hai già fatto, segui il Passaggio 1 dell’implementazione del flusso ottico sparse per configurare l’ambiente.

Avanti, apri dense-starter.py con il tuo editor di testo. Scriveremo tutto il codice in questo file Python.

Configurazione di OpenCV per leggere un video

Farneback Optical Flow

Gunnar Farneback ha proposto una tecnica efficace per stimare il movimento di caratteristiche interessanti confrontando due fotogrammi consecutivi nel suo articolo Stima del movimento a due fotogrammi basata sull’espansione polinomiale.

In primo luogo, il metodo approssima le finestre (vedere la sezione Lucas Kanade dell’implementazione del flusso ottico sparse per maggiori dettagli) dei fotogrammi dell’immagine mediante polinomi quadratici attraverso la trasformazione di espansione polinomiale. In secondo luogo, osservando come il polinomio si trasforma sotto traslazione (movimento), viene definito un metodo per stimare i campi di spostamento dai coefficienti di espansione polinomiale. Dopo una serie di perfezionamenti, viene calcolato il flusso ottico denso. La carta di Farneback è abbastanza concisa e semplice da seguire, quindi consiglio vivamente di passare attraverso la carta se si desidera una maggiore comprensione della sua derivazione matematica.

Per l’implementazione di OpenCV, calcola la grandezza e la direzione del flusso ottico da un array a 2 canali di vettori di flusso \((dx/dt, dy/dt)\), il problema del flusso ottico. Quindi visualizza l’angolo (direzione) del flusso per tonalità e la distanza (grandezza) del flusso per valore della rappresentazione del colore HSV. La forza di HSV è sempre impostata su un massimo di 255 per una visibilità ottimale. La documentazione dell’implementazione di OpenCV del metodo Farneback tramite calcOpticalFlowFarneback() può essere trovata qui.

Visualizzando

E il gioco è fatto! Aprire il terminale ed eseguire

python dense-starter.py

per testare l’implementazione del flusso ottico denso. 👏

Nel caso in cui hai perso qualsiasi codice, il codice completo può essere trovato in dense-solution.py.

Flusso ottico usando il Deep Learning

Mentre il problema del flusso ottico è stato storicamente un problema di ottimizzazione, i recenti approcci applicando il deep learning hanno mostrato risultati impressionanti. Generalmente, tali approcci prendono due fotogrammi video come input per emettere il flusso ottico( immagine con codice colore), che può essere espresso come:

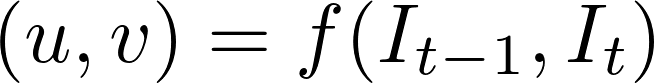
dove \(u\) è il movimento in \(x\) direzione, \(v\) è il movimento in \(y\) direzione e \(f\) è una rete neurale che prende in due fotogrammi consecutivi \(I_{t-1}\) (fotogramma alla volta = \(t-1)\) e \(I_t\) (fotogramma alla volta = \(t)\) come input.

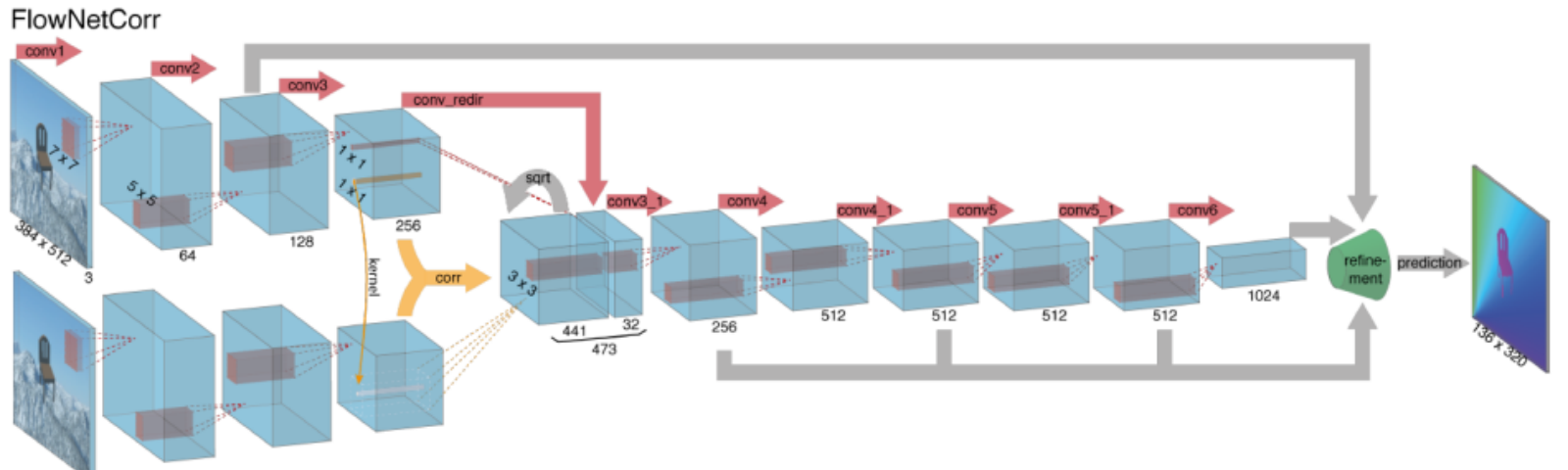
Il calcolo del flusso ottico con reti neurali profonde richiede grandi quantità di dati di allenamento che sono particolarmente difficili da ottenere. Questo perché l’etichettatura delle riprese video per il flusso ottico richiede di capire con precisione il movimento esatto di ogni punto di un’immagine per una precisione subpixel. Per affrontare il problema dell’etichettatura dei dati di formazione, i ricercatori hanno utilizzato la computer grafica per simulare enormi mondi realistici. Poiché i mondi sono generati dall’istruzione, il movimento di ogni punto di un’immagine in una sequenza video è noto. Alcuni esempi di tali includono MPI-Sintel, un film CGI open-source con l’etichettatura del flusso ottico reso per varie sequenze, e Sedie volanti, un set di dati di molte sedie che volano attraverso sfondi casuali anche con l’etichettatura del flusso ottico.

Risolvere i problemi di flusso ottico con il deep learning è un argomento estremamente caldo al momento, con varianti di FlowNet, SPyNet, PWC-Net e altro ancora che si superano l’un l’altro su vari benchmark.

Applicazione del flusso ottico: Segmentazione semantica

Il campo del flusso ottico è una vasta miniera di informazioni per la scena osservata. Man mano che le tecniche per determinare con precisione il flusso ottico migliorano, è interessante vedere le applicazioni del flusso ottico in congiunzione con diversi altri compiti fondamentali di visioni informatiche. Ad esempio, il compito della segmentazione semantica è quello di dividere un’immagine in serie di regioni corrispondenti a classi di oggetti univoche, ma oggetti posizionati strettamente con trame identiche sono spesso difficili per le tecniche di segmentazione a fotogramma singolo. Se gli oggetti sono posizionati separatamente, tuttavia, i movimenti distinti degli oggetti possono essere molto utili dove la discontinuità nel campo del flusso ottico denso corrisponde ai confini tra gli oggetti.

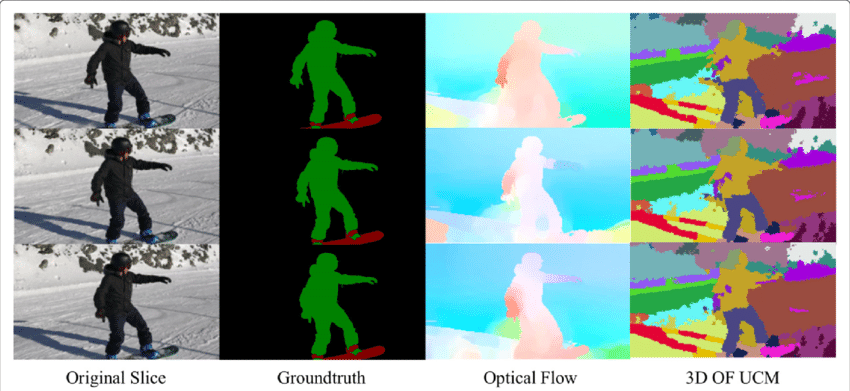
Applicazione del flusso ottico: Rilevamento di oggetti & Tracciamento

Un’altra promettente applicazione del flusso ottico può essere con rilevamento e tracciamento di oggetti o, in una forma di alto livello, verso la costruzione di sistemi di tracciamento e analisi del traffico in tempo reale. Poiché il flusso ottico sparso utilizza il tracciamento dei punti di interesse, tali sistemi in tempo reale possono essere eseguiti con tecniche di flusso ottico basate su funzionalità da una telecamera fissa o da telecamere collegate ai veicoli.

Conclusione

Fondamentalmente, i vettori di flusso ottico funzionano come input per una miriade di attività di livello superiore che richiedono la comprensione della scena delle sequenze video, mentre queste attività possono fungere da elementi costitutivi di sistemi ancora più complessi come l’analisi dell’espressione facciale, la navigazione autonoma del veicolo e molto altro. Le nuove applicazioni per il flusso ottico ancora da scoprire sono limitate solo dall’ingegnosità dei suoi progettisti.

Pigro per codificare, non vuoi spendere per le GPU? Oltre al capo Nanonets e costruire modelli di computer vision gratis!