Supervisionato l’Inferenza Bayesiana (riduzione delle dimensioni e dissotterrare caratteristiche)
Basso livello di funzionalità di rilevamento utilizzando bordi

Infine, il momento che tutti aspettavano per, il prossimo supervisionato l’inferenza Bayesiana serie: la Nostra (non è così) immersione profonda in Operatore di Sobel.
Un algoritmo di rilevamento dei bordi davvero magico, consente l’estrazione di funzionalità di basso livello e la riduzione della dimensionalità, riducendo essenzialmente il rumore nell’immagine. È stato particolarmente utile nelle applicazioni di riconoscimento facciale.
Il 1968 figlio d’amore di Irwin Sobel e Gary Feldman (Stanford Artificial Intelligence Laboratory), questo algoritmo è stato l’ispirazione di molte moderne tecniche di rilevamento dei bordi. Convolvendo due kernel o maschere opposte su una data immagine (ad es. vedi sotto-sinistra) (ciascuno in grado di rilevare i bordi orizzontali o verticali), possiamo creare una rappresentazione meno rumorosa e levigata (vedi sotto-destra).
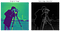
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel valori (solitamente luminanza) differenziando la differenza tra ogni pixel (il pixel di ancoraggio) e i suoi pixel circostanti (essenzialmente approssimando la derivata di un’immagine).
Ciò si traduce in levigatura dell’immagine originale e produzione di un output di dimensione inferiore, in cui le caratteristiche geometriche di basso livello possono essere viste più chiaramente. Questi output possono quindi essere utilizzati come input in algoritmi di classificazione più complessi o come esempi utilizzati per il clustering probabilistico non supervisionato tramite Kullback-Leibler Divergence (KLD) (come visto nel mio recente blog su LBP).
Generare la nostra uscita di dimensione inferiore ci richiede di prendere la derivata dell’immagine. Innanzitutto, calcoliamo il derivato in entrambe le direzioni x e y. Creiamo due kernel 3×3 (vedi matrici), con zeri lungo il centro dell’asse corrispondente, due nei quadrati centrali perpendicolari allo zero centrale e uno in ciascuno degli angoli. Ciascuno dei valori diversi da zero dovrebbe essere positivo in alto/a destra degli zeri (dipendente dall’asse) e negativo sul loro lato corrispondente. Questi kernel sono chiamati Gx e Gy.
Questi appaiono nel formato:
Questi kernel verranno quindi convolti sopra la nostra immagine, posizionando il pixel centrale di ogni kernel su ogni pixel nell’immagine. Usiamo la moltiplicazione della matrice per calcolare il valore di intensità di un nuovo pixel corrispondente in un’immagine di output, per ogni kernel. Pertanto, finiamo con due immagini di output (una per ogni direzione cartesiana).
Lo scopo è trovare la differenza/cambiamento tra il pixel nell’immagine e tutti i pixel nella matrice del gradiente (kernel) (Gx e Gy). Più matematicamente, questo può essere espresso come.
Nota a margine:
Tecnicamente non stiamo convolvendo nulla. Anche se ci piace fare riferimento a ‘circonvoluzioni’ in AI e cerchi di apprendimento automatico, una convoluzione comporterebbe lanciando l’immagine originale. Matematicamente parlando, quando ci riferiamo alle circonvoluzioni, stiamo davvero calcolando la correlazione incrociata tra ogni area 3×3 dell’input e la maschera per ogni pixel. L’immagine di output è la covarianza complessiva tra la maschera e l’input. Ecco come vengono rilevati i bordi.
Torna alla nostra spiegazione Sobel
I valori calcolati per ogni moltiplicazione della matrice tra la maschera e la sezione 3×3 dell’input vengono sommati per produrre il valore finale per il pixel nell’immagine di output. Questo genera una nuova immagine che contiene informazioni sulla presenza di bordi verticali e orizzontali presenti nell’immagine originale. Questa è una rappresentazione caratteristica geometrica dell’immagine originale. Inoltre, poiché questo operatore è garantito per produrre lo stesso output ogni volta, questa tecnica consente un rilevamento stabile dei bordi per le attività di segmentazione dell’immagine.
Da queste uscite, siamo in grado di calcolare sia il gradiente di grandezza e la direzione del gradiente (utilizzando l’arcotangente operatore) in un dato pixel (x,y):
Da questo si può accertare che quei pixel grandi grandezze sono più probabilità di essere un bordo dell’immagine, mentre la direzione ci informa sull’orlo di orientamento (anche se la direzione non è necessario per generare la nostra uscita).
Una semplice implementazione:
Ecco una semplice implementazione dell’operatore Sobel in python (usando NumPy) per darti un’idea del processo (per tutti voi programmatori in erba là fuori).
Questa implementazione python variante di Wikipedia pseudocodice esempio, che mira a mostrare come si potrebbe implementare questo algoritmo, al contempo, a dimostrazione delle varie fasi del processo.
Perché ci interessa?
Sebbene l’approssimazione del gradiente prodotta da questo operatore sia relativamente grezza, fornisce un metodo estremamente efficiente dal punto di vista computazionale per calcolare bordi, angoli e altre caratteristiche geometriche delle immagini. A sua volta, ha aperto la strada a una serie di tecniche di riduzione della dimensionalità e di estrazione delle funzionalità, come i modelli binari locali (vedi il mio altro blog per maggiori dettagli su questa tecnica).
Affidarsi a caratteristiche esclusivamente geometriche rischia di perdere informazioni importanti durante la codifica dei nostri dati, tuttavia, il trade-off è ciò che consente una rapida pre-elaborazione dei dati e, a sua volta, un allenamento veloce. Pertanto questa tecnica è particolarmente utile in scenari in cui la trama e le caratteristiche geometriche possono essere considerate molto importanti nella definizione dell’input. Questo è il motivo per cui il riconoscimento facciale può essere completato con un grado di precisione relativamente elevato utilizzando l’operatore Sobel. Tuttavia, questa tecnica potrebbe non essere la scelta migliore se si cerca di classificare o raggruppare input che utilizzano il colore come principale fattore di differenziazione.
Questo metodo è ancora estremamente efficace per ottenere una rappresentazione a bassa dimensione di caratteristiche geometriche e un ottimo punto di partenza per la dimensionalità e la riduzione del rumore, prima di utilizzare altri classificatori o per l’uso in metodologie di inferenza bayesiana.