La matematica di rilievo: Parte II. Il planimetro

Pubblicato giugno 2008.

La seconda delle due colonne sulla matematica del rilievo (la prima è qui). …

Bill Casselman
Università della Columbia Britannica, Vancouver, Canada
cass at math.ubc.ca

John Eggers
Università della California, San Diego
jeggers presso ucsd.edu

e-Mail ad un amico

Stampa questo articolo

Un planimetro è un tavolo di strumento per la misura delle aree, di solito le aree irregolari regioni su una mappa o di una fotografia. Una volta erano comuni, ma ora sono stati in gran parte sostituiti da strumenti digitali.

L’immagine seguente dà un’idea del setup. Il braccio del palo ruota liberamente attorno al palo, che è fissato sul tavolo. Il braccio tracciante ruota attorno al perno, che è dove si unisce al braccio polare. Si traccia una curva in senso orario con il tracciante, e come si fa così rotola ruota di misura lungo, e la distanza totale rotola viene accumulato sul quadrante. La ruota di supporto mantiene la cosa da flopping over. Alla fine, si legge un numero dal quadrante e, dopo la moltiplicazione per un fattore che dipende solo dalla particolare configurazione del planimetro, si ottiene l’area all’interno della curva.

La figura successiva offre una visione migliore del meccanismo.

Chiamiamo il carrello l’assemblaggio di ruote, quadrante e perno. Nella foto successiva si ottiene uno sguardo migliore a esso, e può vedere l’unità a vite senza fine che provoca la manopola per ruotare come la ruota di misura si muove.

Ecco il diagramma del planimetro originale, tratto dall’articolo di Jakob Amsler che lo ha introdotto:

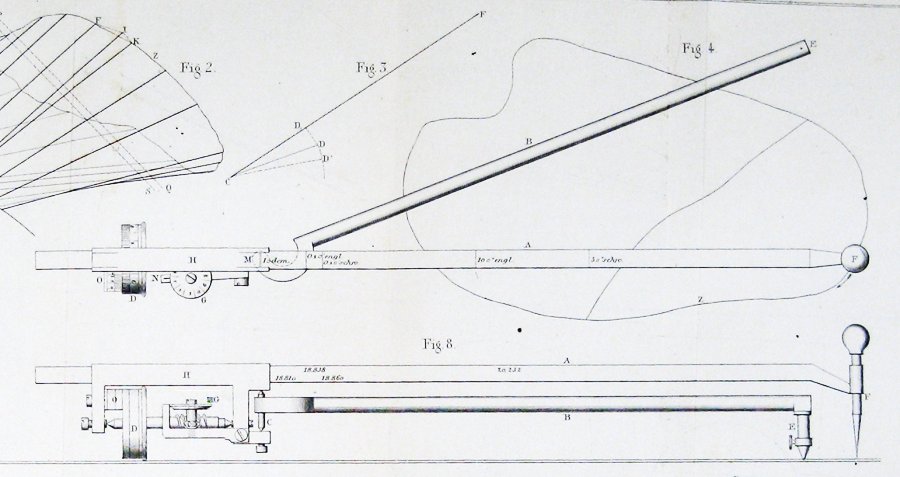
Come può una cosa così semplice misurare le aree?

Geometria del planimetro

Il movimento in senso orario del planimetro è la direzione opposta a quella che i matematici hanno deciso dovrebbe essere rotazione positiva. Invece di violare questa convenzione, lavoreremo d’ora in poi con il planimetro di un matematico, in cui ci si sposta in senso antiorario. Come le fantasie di altri matematici, non ce ne sono sul pianeta!

Esistono alcune restrizioni su come posizionare il planimetro rispetto alla curva che si desidera tracciare. Il carrello può essere fatto scorrere lungo il braccio tracciante, ma in tutti i casi la lunghezza l del braccio tracciante è inferiore alla lunghezza r del braccio del palo. Ciò significa che il tracciante non può mai raggiungere una distanza r – l del polo. D’altra parte, quando è completamente esteso, il tracciante non può mai andare oltre r + l. Quindi la curva da tracciare deve trovarsi all’interno dell’anello tra due cerchi, uno con raggio r – l, l’altro r + l.

Infatti, dovrebbe diventare chiaro in un attimo che i bracci non dovrebbero mai essere completamente estesi, quindi la curva da tracciare deve trovarsi completamente all’interno dell’anello. Inoltre, normalmente il palo è posizionato all’esterno della curva.

Per un dato punto dell’anello ci sono esattamente due possibili configurazioni del planimetro che posizionano il tracciante su quel punto. Scegliere un punto o l’altro significa scegliere un segno per una radice quadrata. Chiamiamo questo scegliere un orientamento per il planimetro. È positivo se la radice quadrata è positiva. Una volta scelto un orientamento, rimarrà lo stesso a meno che il braccio non sia completamente esteso. Questo non deve mai accadere. Finché la curva è interamente all’interno dell’anello, le configurazioni del planimetro varieranno in modo uniforme e univoco con il percorso del tracciante.

La prossima cosa da fare è capire alcune cose sul movimento della ruota di misurazione. Come mostra l’immagine seguente, se la ruota percorre in linea retta una distanza C, la ruota ruota attraverso un angolo θ = C/R dove R è il suo raggio.

Quindi è proprio vero che la rotazione della ruota e la distanza percorsa dal braccio tracciante hanno una qualche relazione tra loro. Ma questa relazione è un po ‘ sottile. Se il braccio si muove dritto a una distanza C, l’area spazzata via sarà lC, ma se si sposta parallelamente a se stesso l’area spazzata via sarà 0. Nel primo caso, un punto sulla circonferenza della ruota sposterà la distanza C. Nel secondo caso, la ruota non si muoverà affatto. E se il braccio si traduce obliquamente, la ruota ruoterà una distanza pari all’altitudine del parallelogramma coperto dal braccio. In tutti i casi in cui il braccio si traduce parallelamente a se stesso, l’area spazzata dalla porzione del braccio tracciante tra il perno e il tracciante sarà uguale a lC, dove C è la distanza misurata dalla rotazione della ruota. Questo è il fatto fondamentale che collega il movimento del braccio al movimento della ruota di misurazione.

Il modo per esprimere questo appunto è che non importa quanto il braccio si muove, misurare la distanza dalla ruota è il percorso integrale

dove Γ è il percorso compiuto dal punto di braccio dove la ruota di misurazione è collegata, n è il vettore unitario perpendicolare al braccio, in qualsiasi momento, e t è il vettore unitario che punta nella direzione di marcia (in modo che, per esempio, se il braccio si muove parallelamente a se stesso il prodotto di puntino di n e t è 0).

Teorema di Guldin

Successivamente cercheremo di rendere intuitivamente chiaro il comportamento del planimetro, ma prima esamineremo un tipo speciale di planimetro, e in questo caso dimostreremo un risultato più generale. Supponiamo di prendere un singolo braccio di lunghezza l che si muove liberamente e di attaccare ad esso una ruota di misurazione del raggio R proprio nel suo centro.

Quindi spostiamo il braccio sull’aereo. Se la ruota di misura ruota attraverso un angolo totale di θ radianti mentre il braccio si muove, la distanza percorsa da un punto sulla circonferenza è C = θR.

Teorema di Guldin. In questa situazione, l’area totale spazzata via dal braccio è il prodotto lC.L’area

qui viene interpretata con un segno. Se il braccio ruota attorno al suo centro, una metà del braccio va avanti e l’altra indietro, e i due si annullano.

Abbiamo già visto che l’affermazione di Guldin è valida nel caso in cui il braccio si traduca. Naturalmente questo non sempre accade – il braccio può ruotare come si muove così come tradurre. Ma possiamo vedere cosa sta succedendo tagliando l’area spazzata come segue:

Poiché la ruota di misurazione si trova al centro del braccio, mentre il braccio ruota, schiaccia i piccoli blocchi da un lato mentre li espande dall’altro. Questi effetti si annullano a vicenda esattamente.

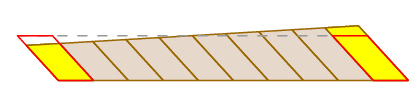
Una prova completamente rigorosa può essere data usando la formula per il cambiamento delle variabili in un integrale doppio e l’espressione per il viaggio della ruota come integrale del percorso.

Ora supponiamo che la ruota sia posizionata da qualche altra parte. Supponiamo che la sua posizione sia c + v dove c è il centro del braccio e v un vettore lungo il braccio. La lunghezza di v rimarrà fissa, diciamo a ρ. Il percorso che la ruota segue è c (t) + v (t). L’integrale del percorso è ora

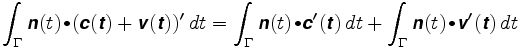
Il primo integrale è la distanza che la ruota percorrerebbe se fosse al centro del braccio. Nel secondo, il vettore v(t) è sempre perpendicolare a n e v (t) ha lunghezza costante. Il vettore v (t) si muove su un cerchio di raggio uguale a ρ. Quindi il prodotto punto di n e v'(t) è solo la lunghezza firmata di v'(t), e il secondo integrale è uguale a ρ volte la rotazione totale del braccio. Quindi:

Se la ruota è a distanza ρ dal centro del braccio, la distanza C che la ruota misura è C0 , la distanza che sarebbe misurata se la ruota fosse al centro, più ρ volte l’angolo totale θ che il braccio ruota.

Puoi vedere immediatamente un semplice caso di questo ruotando il braccio attorno al suo centro. Combinando questo con il teorema di Guldin, vediamo che in tutti i casi:

C = C0 + ρ θ
Area swept out = l C0 = l C – l ρ θ

Il risultato completo

La Formula di Guldin dà un’area firmata – se si spazza all’indietro su un’area, la ruota va all’indietro e si annulla l’area che si è già coperta. Se applichiamo questo al caso in cui il braccio libero ritorna esattamente al punto in cui è iniziato, vediamo che lC è uguale all’area della regione chiusa tracciata dall’estremità destra del braccio meno quella della regione spazzata da quella sinistra.

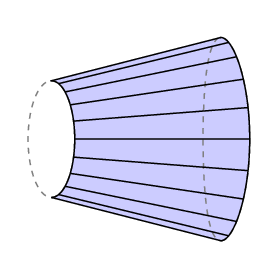
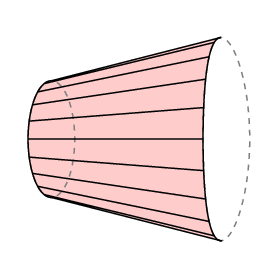
Nel caso del planimetro polare, la parte inferiore del braccio è limitata ad un arco di cerchio di raggio r con centro al polo, quindi l C è l’area tracciata dal tracciante. Inoltre, normalmente il polo si trova al di fuori della regione da misurare, e in questo caso la quantità totale di rotazione del braccio deve essere 0. Quindi in questo caso abbiamo

l’Area della regione tracciata = lC

Ecco la figura incluso da Jakob Amsler, l’inventore, nella sua carta originale dello strumento da lui inventato:

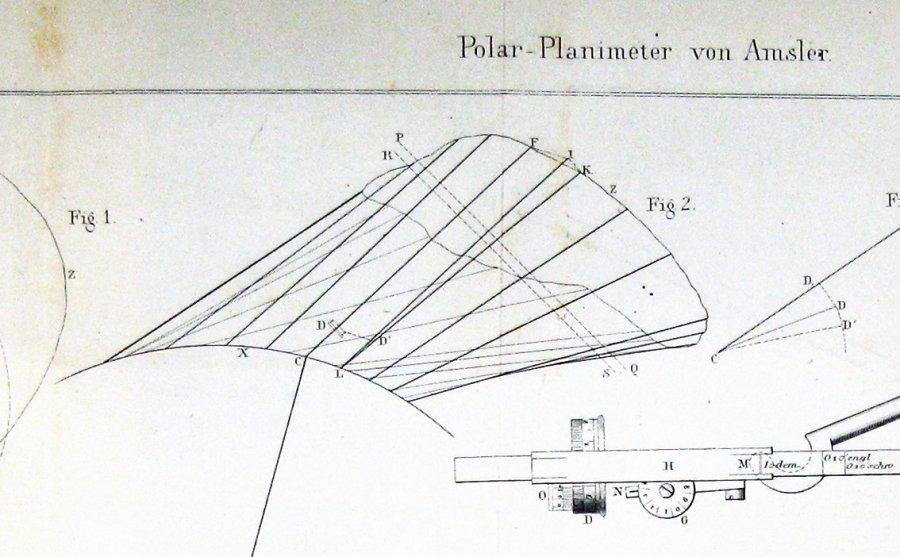
mi sembra abbastanza chiaro da questo che Amsler derivato la sua costruzione attraverso una qualche forma di Guldin teorema.

Planimetri e Teorema di Green

Come abbiamo già detto, avendo scelto l’orientamento del planimetro, la configurazione del planimetro è una funzione continua della posizione del tracciante. Diciamo che scegliamo l’orientamento positivo. Quindi possiamo collegare a ciascun punto dell’anello un vettore unitario n, quello che punta in senso antiorario e perpendicolare al braccio tracciante sul tracciante.

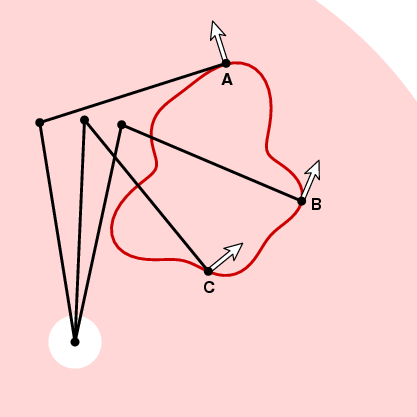
Il modo in cui la ruota di misura risponderà al movimento lungo la curva nell’istante successivo dipende dall’angolo tra questo vettore e il vettore tangente unitario della curva. In A nella foto sopra, la ruota di misurazione non si muoverà perché il movimento lungo la curva è parallelo al braccio tracciante. A B se il tracciante si muove una piccola distanza ds, così sarà la ruota di misura. E a C la ruota di misurazione si muoverà una certa distanza tra 0 e ds. Per essere precisi, supponiamo che t sia il vettore tangente unitario ad un certo punto della curva. Se il tracciante sposta la distanza ds lungo la curva, a quel punto la ruota di misurazione sposterà una distanza d ds, dove d = n . t, il prodotto dot dei vettori unitari t e n. In altre parole, se ci muoviamo attorno alla curva Γ la ruota di misurazione sposterà una distanza totale uguale all’integrale di n . t ds (dot product), o

Ma poiché ogni punto dell’anello corrisponde ad una configurazione positiva unica del planimetro, possiamo assegnare un vettore n ad ogni punto interno dell’anello, e quindi definisce un campo vettoriale. La curva Γ è il confine del suo interno Ω, e da una delle nostre ipotesi questo è contenuto interamente nella regione in cui è definito n. Il teorema di Green ci dice che l’integrale del percorso attorno al confine di questa regione è anche uguale a un certo integrale su Ω: Quindi

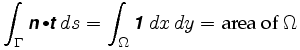
Più precisamente, il Teorema di Green ci dice che

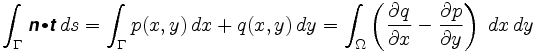
dove n = è il campo vettoriale coinvolto. L’integrando nel doppio integrale è chiamato il ricciolo del campo vettoriale.

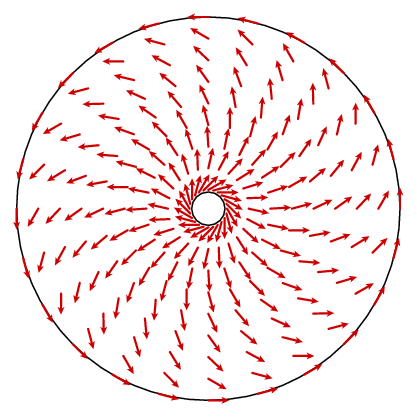
Questo non sembra portarci molto lontano. Quello che dovrebbe accadere è che il ricciolo è una costante 1. In linea di principio, potremmo trovare una formula per il campo vettoriale n e calcolare il suo ricciolo, ma non è molto illuminante. Possiamo approfittare di un altro fatto, tuttavia. Il campo vettoriale ha simmetria circolare, il che significa che è determinato da ciò che è su un raggio. La legge del coseno ci dà una formula semplice per la componente circonferenziale.

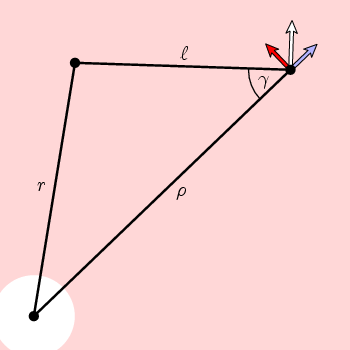
segue dalla semplice geometria in questa figura che la componente circonferenziale di n è

f(ρ) = cos(γ) = (r 2 + r 2 – r 2)/(2 ρ l)

Il vero punto di Verde Teorema è che, al fine di verificare che il integrand è 1, è sufficiente verificare che il percorso integrale di tutto adatto piccoli sentieri è la stessa dell’area. Per questo, scegliamo le nostre regioni per essere come qui:

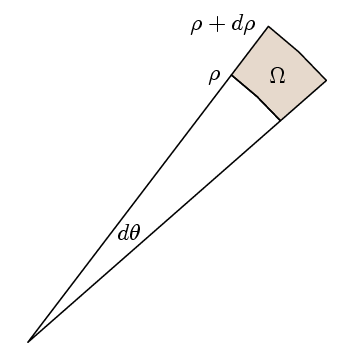
Quindi l volte l’integrale del percorso è

l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ

o

(θ/2) ( (ρ + dp) 2 – ρ 2)

che è l’area della regione Ω.

Altri tipi di planimetri

Il teorema di Guldin implica che il movimento di una ruota di misurazione ti dirà l’area tracciata dal tracciante ogni volta che il braccio con una ruota di misurazione su di esso traccia una curva ma ha un’estremità limitata a una curva unidimensionale. Ciò accade, ad esempio, con il planimetro di rotolamento, in cui il perno è limitato a una linea retta essendo su un cilindro di rotolamento.

Per saperne di più

• produce e vende ancora planimetri.
• Calcolo differenziale e integrale Volume II, R. Courant, Blackie & Son, 1936. La sezione sulla Formula di Guldin (pp. 294-298) offre una spiegazione di come funziona il planimetro.
• Amsler’s original article, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Mancano i diagrammi, ma sono qui:
  • Primo diagramma di Amsler
  • Secondo diagramma di Amsler

  Ringraziamo Donna Sammis della Stony Brook University Library per aver individuato l’articolo e suo marito Robert per aver fornito fotografie delle figure.

  L’azienda fondata da Amsler ha prodotto strumenti fino al 20 ° secolo. Questa fotografia mostra il logo, su una versione a pantografo del planimetro:

  

• “About Planimeters,” EngineerSupply. La società ha anche pubblicato un video su YouTube.

Bill Casselman
University of British Columbia, Vancouver, Canada
cass a per la matematica.ubc.ca

Giovanni Eggers
Università di California, San Diego
jeggers a ucsd.edu

Coloro che possono accedere JSTOR è possibile trovare alcuni dei documenti citati sopra. Per quelli con accesso, MathSciNet della American Mathematical Society può essere utilizzato per ottenere ulteriori informazioni bibliografiche e recensioni di alcuni di questi materiali. Alcune delle voci di cui sopra sono accessibili tramite il portale ACM , che fornisce anche servizi bibliografici.