Understanding Deep Residual Networks

Deep Residual networks (ResNet) ha preso d’assalto il mondo dell’apprendimento profondo quando Microsoft Research ha rilasciato Deep Residual Learning per il riconoscimento delle immagini. Queste reti hanno portato alla vittoria del 1 ° posto in tutte e cinque le tracce principali dei concorsi ImageNet e COCO 2015, che hanno riguardato la classificazione delle immagini, il rilevamento di oggetti e la segmentazione semantica. La robustezza delle ResNet è stata dimostrata da varie attività di riconoscimento visivo e da attività non visive che coinvolgono la parola e il linguaggio. Ho anche usato ResNet in aggiunta ad altri modelli di apprendimento profondo nella mia ricerca tesi di dottorato.

Questo post riassumerà i tre documenti qui sotto, che sono tutti scritti o co-scritti dall’inventore di ResNet Kaiming He, perché credo che i documenti originali forniscano la spiegazione più intuitiva e dettagliata del modello/delle reti. Speriamo che questo post possa aiutarti a comprendere meglio l’essenza delle reti residue.

• Profondità di Residui di Apprendimento per il Riconoscimento di Immagini
• Identity mapping nel Profondo Residuo Reti.
• Aggregati Residuo di Trasformazione Profonda Reti Neurali

l’Intuizione Profonda Residuo di Rete (stackoverflow ref)

Un residuo di blocco viene visualizzata come segue:

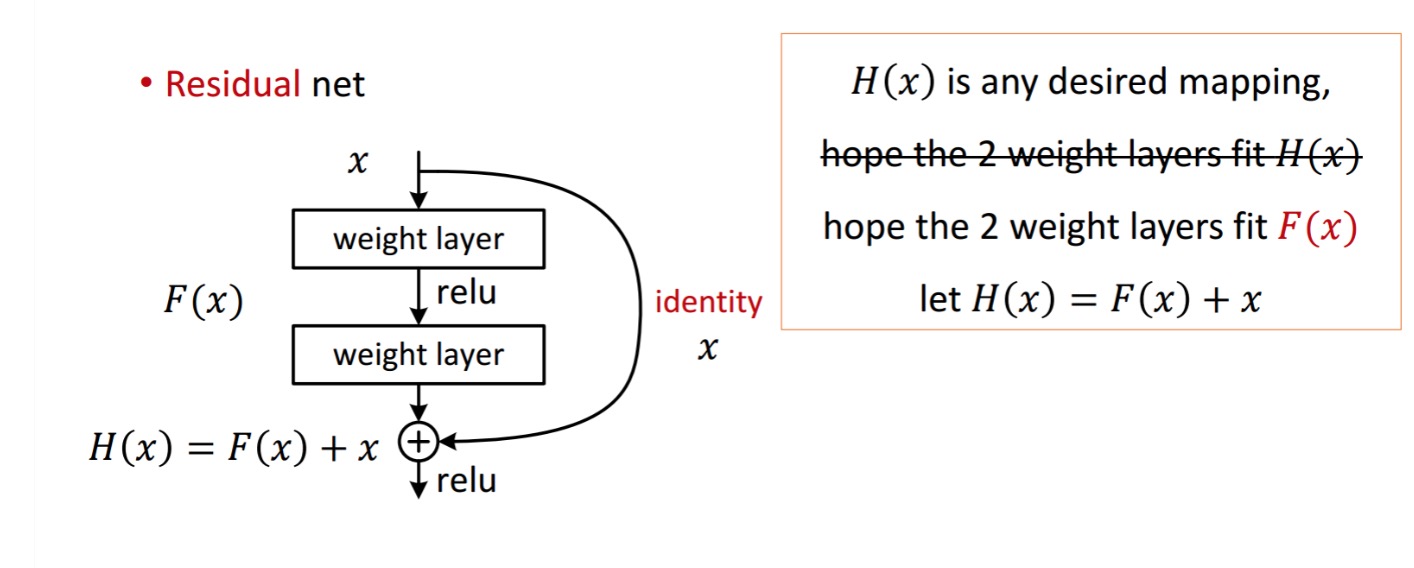
le residue unità ottiene dalla lavorazione con un peso di strati. Quindi aggiunge per ottenere . Ora, supponiamo che sia il tuo output ideale previsto che corrisponda alla tua verità di base. Dal momento che, ottenere il desiderato dipende da ottenere il perfetto . Ciò significa che i due strati di peso nell’unità residua dovrebbero effettivamente essere in grado di produrre il desiderato , quindi ottenere l’ideale è garantito.

è ottenuto come segue.

è ottenuto come segue.

Gli autori ipotizzano che la mappatura residua (cioè ) possa essere più facile da ottimizzare di . Per illustrare con un semplice esempio, si supponga che l’ideale . Quindi per una mappatura diretta sarebbe difficile imparare una mappatura dell’identità in quanto esiste una pila di livelli non lineari come segue.

Quindi, approssimare la mappatura dell’identità con tutti questi pesi e ReLUs nel mezzo sarebbe difficile.

Ora, se definiamo la mappatura desiderata, abbiamo solo bisogno di ottenere come segue.

Raggiungere quanto sopra è facile. Basta impostare qualsiasi peso a zero e si otterrà un’uscita zero. Aggiungi indietro e ottieni la mappatura desiderata.

Deep Residual Learning for Image Recognition

Problema

Quando le reti più profonde iniziano a convergere, è stato esposto un problema di degradazione: con l’aumento della profondità della rete, la precisione si satura e quindi si degrada rapidamente.

Seeing Degrading in Action:

Prendiamo una rete poco profonda e la sua controparte più profonda aggiungendo più livelli ad essa.

Scenario peggiore: i primi livelli del modello più profondo possono essere sostituiti con una rete superficiale e i livelli rimanenti possono semplicemente agire come una funzione di identità (Input uguale all’output).

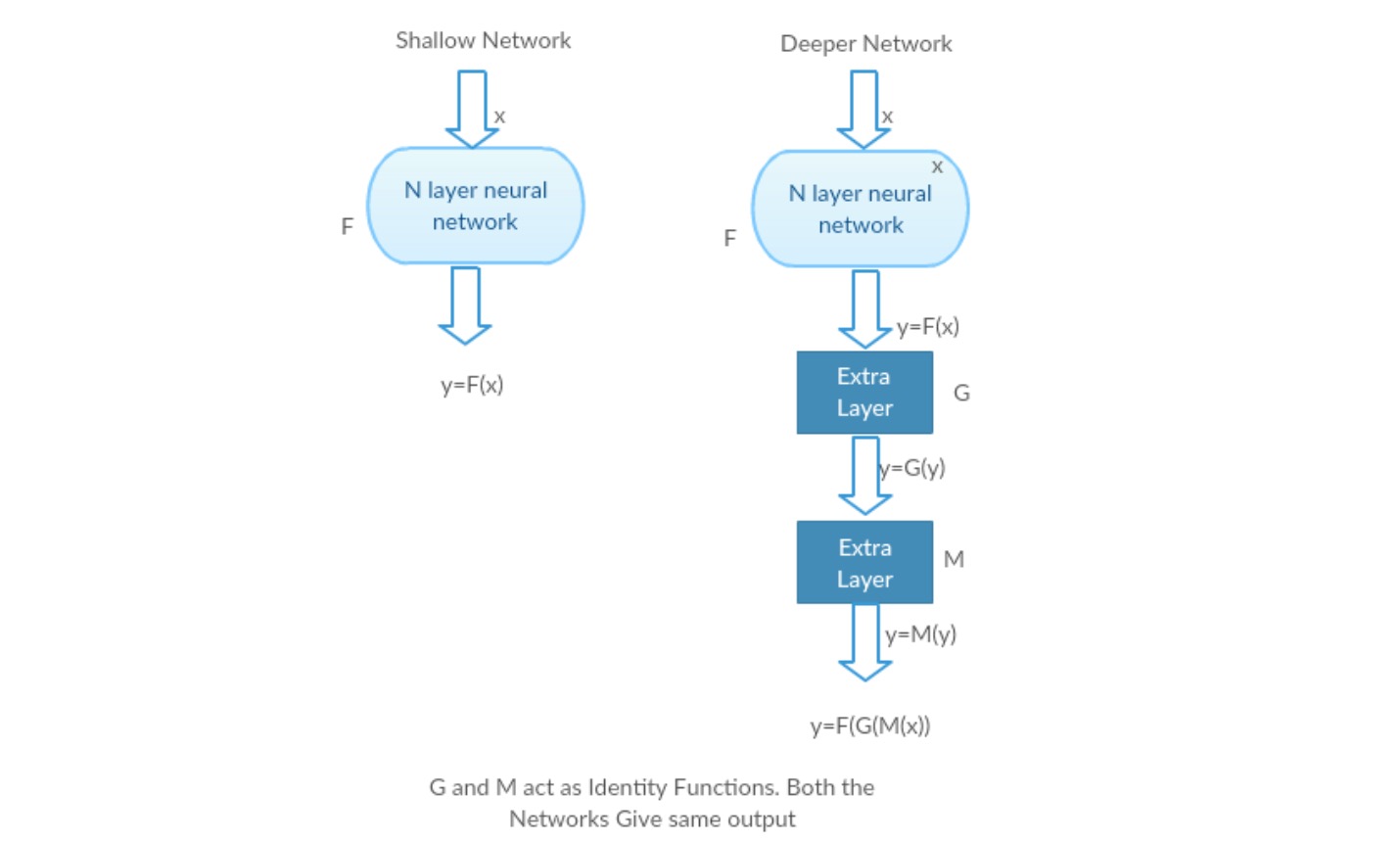
Scenario gratificante: nella rete più profonda i livelli aggiuntivi approssimano meglio la mappatura rispetto alla parte contatore più bassa e riducono l’errore di un margine significativo.

Esperimento: Nel peggiore dei casi, sia la rete superficiale che la variante più profonda dovrebbero dare la stessa precisione. Nel caso di scenario gratificante, il modello più profondo dovrebbe fornire una precisione migliore rispetto alla parte inferiore del contatore. Ma gli esperimenti con i nostri risolutori attuali rivelano che i modelli più profondi non funzionano bene. Quindi l’utilizzo di reti più profonde sta degradando le prestazioni del modello. Questi documenti cercano di risolvere questo problema utilizzando Deep Residual learning framework.

Come risolvere?

Invece di imparare una mappatura diretta di con una funzione (alcuni livelli non lineari impilati). Definiamo la funzione residua usando, che può essere riformulata in, dove e rappresenta rispettivamente i livelli non lineari impilati e la funzione di identità(input=output).

L’ipotesi dell’autore è che sia facile ottimizzare la funzione di mappatura residua piuttosto che ottimizzare la mappatura originale non referenziata .

Intuizione dietro i blocchi residui:

Prendiamo come esempio la mappatura dell’identità (ad esempio ). Se la mappatura dell’identità è ottimale, possiamo facilmente spingere i residui a zero () piuttosto che adattare una mappatura dell’identità () da una pila di livelli non lineari. In un linguaggio semplice è molto facile trovare una soluzione come piuttosto che usare stack di livelli cnn non lineari come funzione (Pensaci). Quindi, questa funzione è ciò che gli autori hanno chiamato funzione residua.

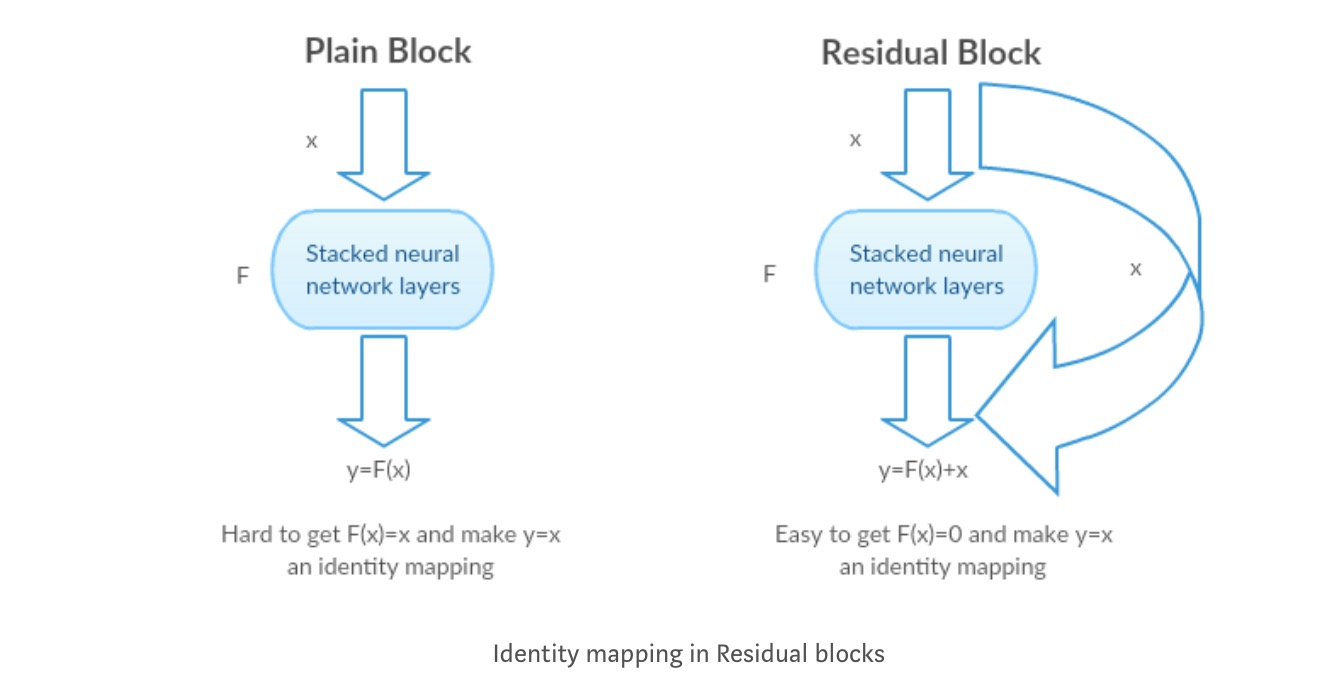
Gli autori hanno fatto diversi test per testare la loro ipotesi. Diamo un’occhiata a ciascuno di loro ora.

Casi di test:

Prendi una rete semplice (VGG tipo 18 layer network) (Network-1) e una variante più profonda di esso (34-layer, Network-2) e aggiungi livelli residui alla Rete-2 (34 layer con connessioni residue, Network-3).

Progettare la rete:

1. Utilizzare 3 * 3 filtri per lo più.
2. Giù campionamento con CNN strati con stride 2.
3. Livello di pooling medio globale e uno strato completamente connesso a 1000 vie con Softmax alla fine.

Esistono due tipi di connessioni residue:

I. Le scorciatoie identity () possono essere utilizzate direttamente quando input () e output () hanno le stesse dimensioni.

II. Quando le dimensioni cambiano, A) Il collegamento esegue ancora il mapping dell’identità, con zero voci aggiuntive riempite con la dimensione aumentata. B) La scorciatoia di proiezione viene utilizzata per abbinare la dimensione (eseguita da 1*1 conv) usando la seguente formula

Risultati

Anche se la rete a 18 livelli è solo il sottospazio nella rete a 34 livelli, funziona ancora meglio. ResNet supera con un margine significativo nel caso in cui la rete è più profondo

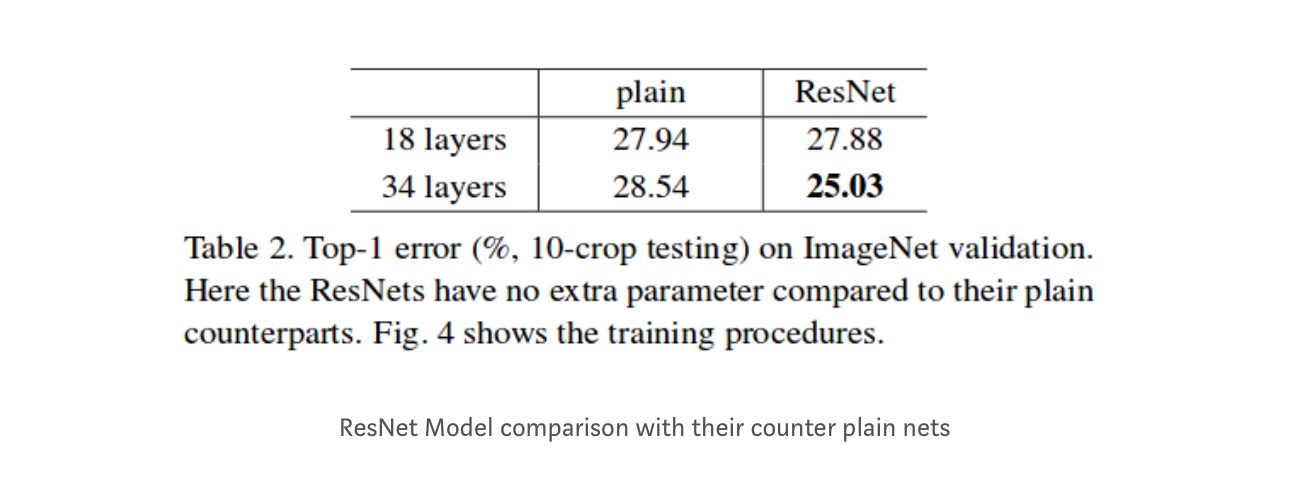
di studi approfonditi

Inoltre, più le reti sono studiato:

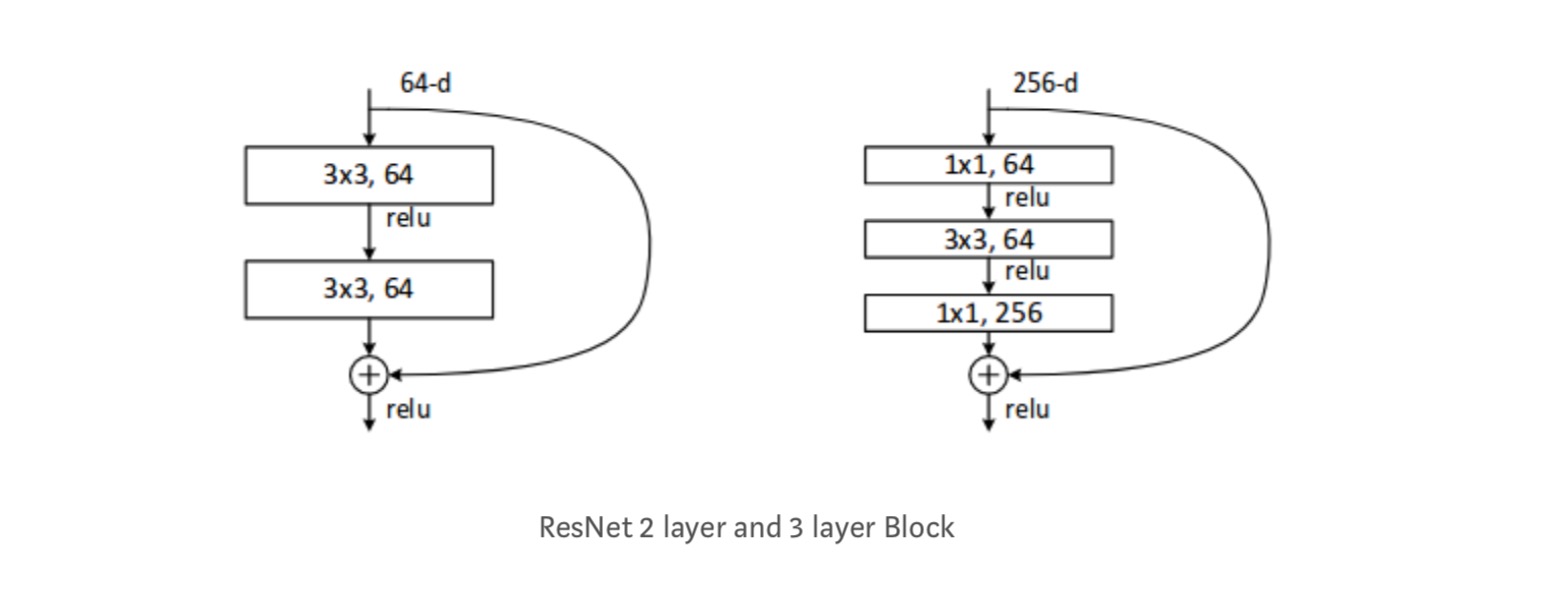
Ogni ResNet blocco è di 2 strati profondi (Utilizzato in reti di piccole dimensioni come ResNet 18, 34) o 3 strati profondi( ResNet 50, 101, 152).

Osservazioni

1. La rete ResNet converge più velocemente rispetto alla semplice parte del contatore.
2. Identità vs shorcuts proiezione. Guadagni incrementali molto piccoli utilizzando scorciatoie di proiezione (Equazione-2) in tutti i livelli. Quindi tutti i blocchi ResNet usano solo scorciatoie di identità con scorciatoie di proiezioni utilizzate solo quando le dimensioni cambiano.
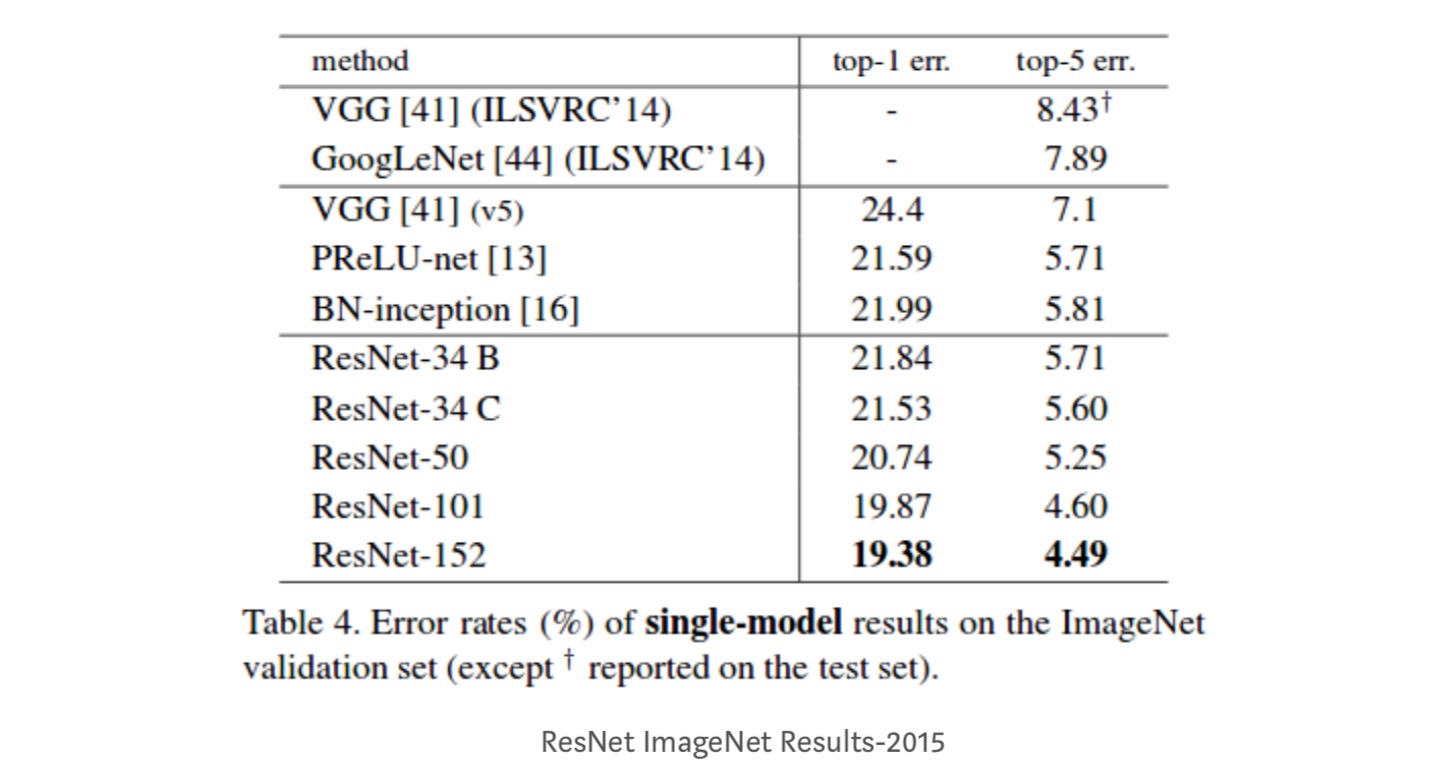
3. ResNet-34 ha ottenuto un errore di convalida top-5 del 5,71% migliore di BN-inception e VGG. ResNet-152 raggiunge un errore di convalida top-5 del 4,49%. Un insieme di 6 modelli con diverse profondità raggiunge un errore di convalida top-5 del 3,57%. Vincere il 1 ° posto in ILSVRC-2015

Identity mapping in Deep Residual Networks

Questo articolo fornisce la comprensione teorica del perché il problema del gradiente di fuga non è presente nelle reti residue e il ruolo delle connessioni skip (le connessioni skip significano l’input or ) sostituendo Identity mapping (x) con funzioni diverse.

Introduzione

Le reti residue profonde sono costituite da molte “Unità residue”impilate. Ogni unità può essere espressa in una forma generale:

dove e sono ingresso e uscita dell’unità, ed è una funzione residua. Nell’ultimo documento, è una mappatura di identità ed è una funzione ReLU.

L’idea centrale delle ResNet è di apprendere la funzione residua additiva rispetto a , con una scelta chiave di utilizzare una mappatura dell’identità . Questo viene realizzato allegando una connessione identity skip (“collegamento”).

In questo articolo, analizziamo le reti residue profonde concentrandosi sulla creazione di un percorso “diretto” per la propagazione delle informazioni — non solo all’interno di un’unità residua, ma attraverso l’intera rete. Le nostre derivazioni rivelano che se entrambi e sono mappature di identità, il segnale potrebbe essere propagato direttamente da un’unità a qualsiasi altra unità, sia nei passaggi avanti che indietro. I nostri esperimenti mostrano empiricamente che l’allenamento in generale diventa più facile quando l’architettura è più vicina alle due condizioni precedenti.

Per comprendere il ruolo delle connessioni skip, analizziamo e confrontiamo vari tipi di . Troviamo che la mappatura dell’identità scelta nell’ultimo documento raggiunge la riduzione degli errori più rapida e la perdita di allenamento più bassa tra tutte le varianti che abbiamo studiato, mentre saltare le connessioni di scaling, gating e circonvoluzioni 1×1 portano a perdite ed errori di allenamento più elevati. Questi esperimenti suggeriscono che mantenere un percorso di informazioni “pulito” è utile per facilitare l’ottimizzazione.

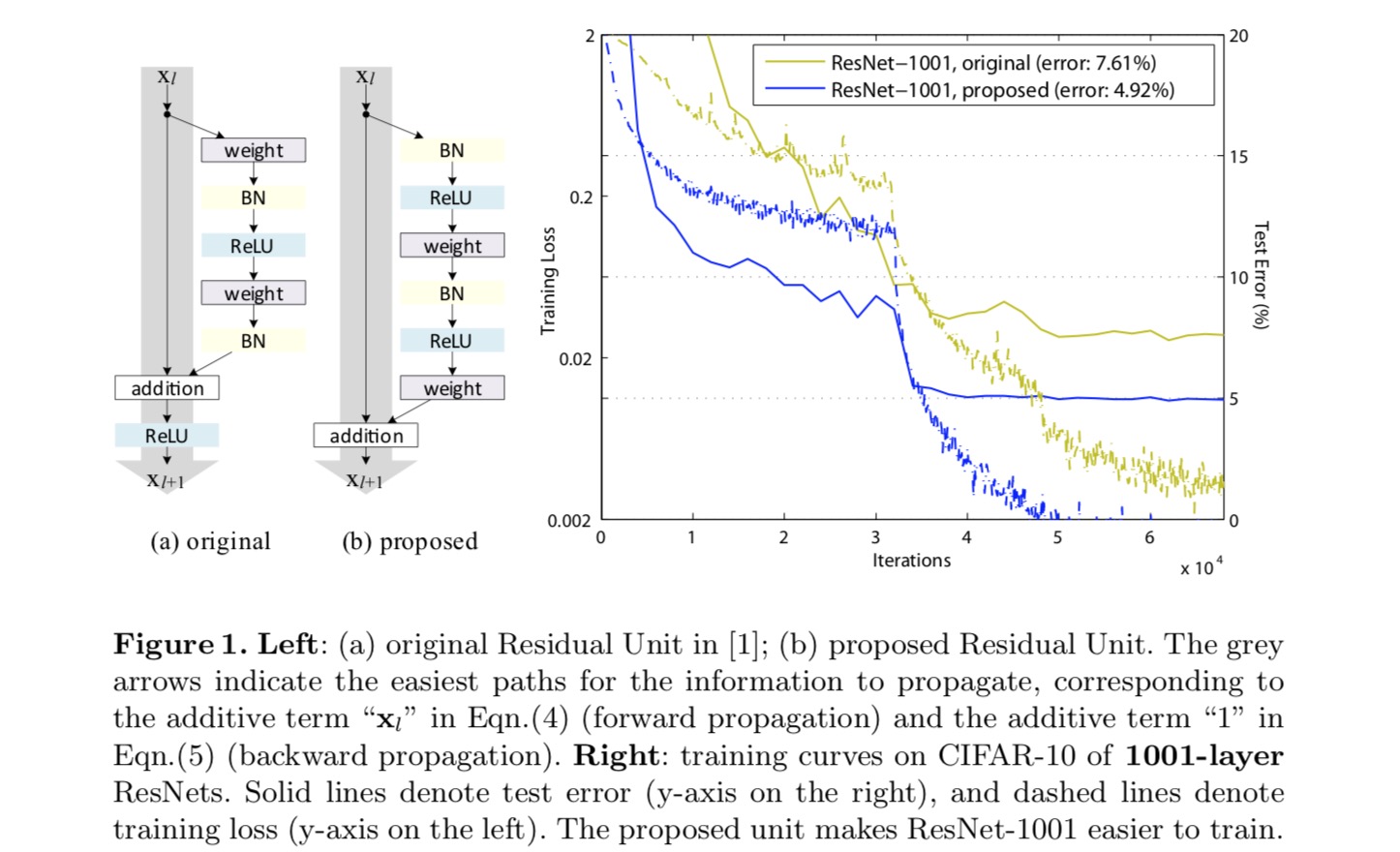
Per costruire una mappatura dell’identità , consideriamo le funzioni di attivazione (ReLU e BN) come “pre-attivazione” dei livelli di peso, in contrasto con la saggezza convenzionale di “post-attivazione”. Questo punto di vista porta ad un nuovo design dell’unità residua, mostrato nella figura seguente. Sulla base di questa unità, presentiamo risultati competitivi su CIFAR-10/100 con un ResNet a 1001 strati, che è molto più facile da addestrare e generalizza meglio del ResNet originale. Riportiamo inoltre risultati migliorati su ImageNet utilizzando un ResNet a 200 strati, per il quale la controparte dell’ultimo documento inizia a sovrapporsi. Questi risultati suggeriscono che c’è molto spazio per sfruttare la dimensione della profondità della rete, una chiave per il successo del moderno apprendimento profondo.

Analisi delle reti Residue profonde

Le ResNet sviluppate nell’ultimo paper sono architetture modularizzate che impilano blocchi di costruzione della stessa forma di collegamento. In questo documento chiamiamo questi blocchi “Unità residue”. L’unità residua originale nell’ultimo documento esegue il seguente calcolo:

Ecco la funzione di input per l’unità residua-esima. è un insieme di pesi (e pregiudizi) associati all’unità residua-esima ed è il numero di strati in un’unità residua ( è 2 o 3 nell’ultima carta). denota la funzione residua, e.g., una pila di due strati convoluzionali 3×3 nell’ultima carta. La funzione è l’operazione dopo aggiunta elemento-saggio, e nell’ultima carta è ReLU. La funzione è impostata come mappatura dell’identità:.

Se è anche una mappatura dell’identità: , possiamo ottenere:

Ricorsivamente avremo:

per qualsiasi unità più profonda e qualsiasi unità meno profonda . Questa equazione presenta alcune niceproperties. (1 )La caratteristica di qualsiasi unità più profonda può essere rappresentata come la caratteristica di qualsiasi unità meno profonda più una funzione residua in una forma di, indicando che il modello è in modo residuo tra qualsiasi unità e. (2) La caratteristica , di qualsiasi unità profonda , è la somma delle uscite di tutte le precedenti funzioni residue (plus). Questo è in contrasto con una “rete semplice” in cui una caratteristica è una serie di prodotti matrice-vettore, ad esempio, (ignorando BN e ReLU).

L’equazione precedente porta anche a buone proprietà di propagazione all’indietro. Denotando la funzione di perdita come, dalla regola della catena di backpropagation abbiamo:

L’equazione precedente indica che il gradiente può essere scomposto in due termini additivi: un termine di che propaga le informazioni direttamente senza riguardo ad alcuni strati del peso ed un altro termine di che propaga attraverso gli strati del peso. Il termine additivo di assicura che le informazioni vengono propagate direttamente a qualsiasi unità meno profonda l.L ” equazione di cui sopra suggerisce anche che è improbabile che il gradiente da annullare per un mini-batch, perché in generale il termine non può essere sempre -1 per tutti i campioni in un mini-batch. Ciò implica che il gradiente di un livello non svanisce anche quando i pesi sono arbitrariamente piccoli.

Le due equazioni precedenti suggeriscono che il segnale può essere propagato direttamente da qualsiasi unità a un’altra, sia in avanti che indietro. Il fondamento delle prime due equazioni precedenti è costituito da due mappature di identità: (1) la connessione di salto dell’identità e (2) la condizione che è una mappatura dell’identità.

Importanza dell’identità salta le connessioni

Consideriamo una semplice modifica, , per rompere la scorciatoia dell’identità:

dove è uno scalare modulante (per semplicità assumiamo ancora l’identità). Applicando ricorsivamente questa formulazione otteniamo un’equazione simile alla precedente:

dove la notazione assorbe gli scalari nelle funzioni residue. Allo stesso modo, abbiamo la backpropagazione della seguente forma:

A differenza dell’equazione precedente, in questa equazione il primo termine additivo è modulato da un fattore . Per una rete estremamente profonda (è grande), se per tutti , questo fattore può essere esponenzialmente grande; se per tutti , questo fattore può essere esponenzialmente piccolo e svanire, il che blocca il segnale backpropagato dalla scorciatoia e lo costringe a fluire attraverso gli strati di peso. Ciò si traduce in difficoltà di ottimizzazione come mostriamo dagli esperimenti.

Nell’analisi precedente, la connessione identity skip originale viene sostituita con un semplice ridimensionamento . Se la connessione skip rappresenta trasformazioni più complicate (come gating e 1×1 circonvoluzioni), nell’equazione precedente il primo termine diventa dove è la derivata di . Questo prodotto può anche impedire la propagazione delle informazioni e ostacolare la procedura di formazione come testimoniato nei seguenti esperimenti.

Esperimenti su connessioni Skip

Sperimentiamo con la ResNet a 110 strati su CIFAR-10. Questo ResNet-110 estremamente profondo ha 54 unità residue a due strati (costituite da 3 × 3 strati convoluzionali) ed è impegnativo per l’ottimizzazione. Vengono sperimentati vari tipi di connessioni di salto. Vedere la figura seguente:

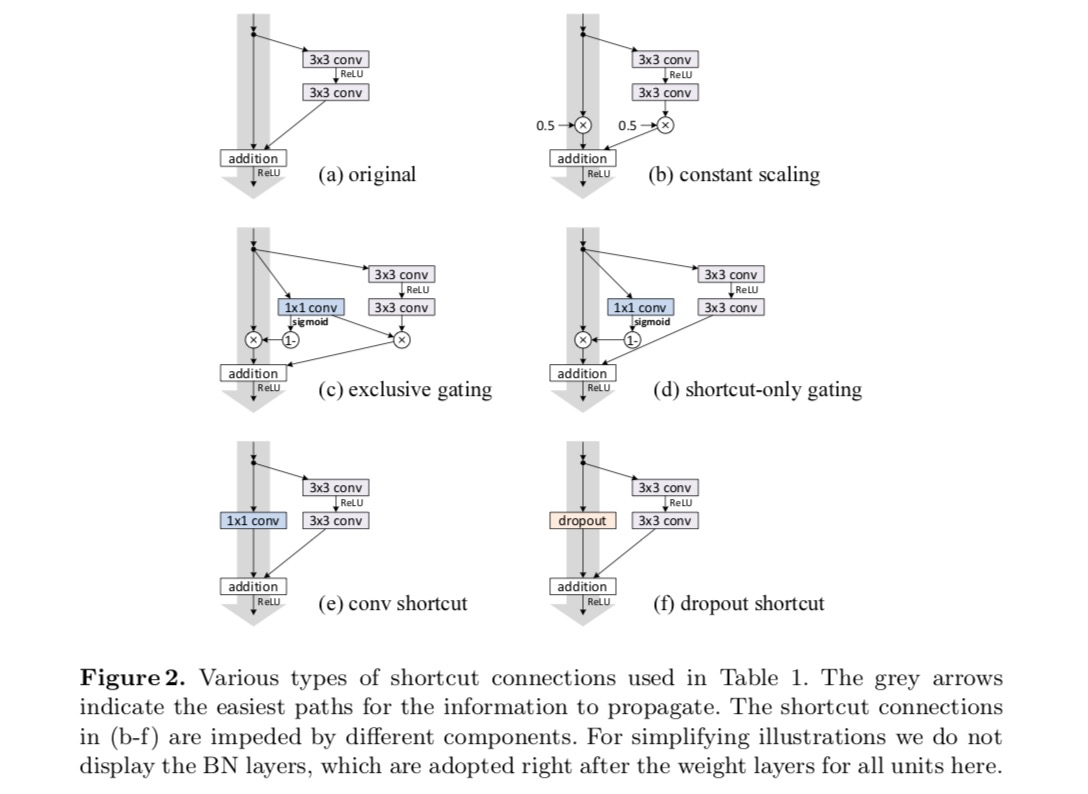
I risultati della classificazione sono visualizzati nella tabella seguente:

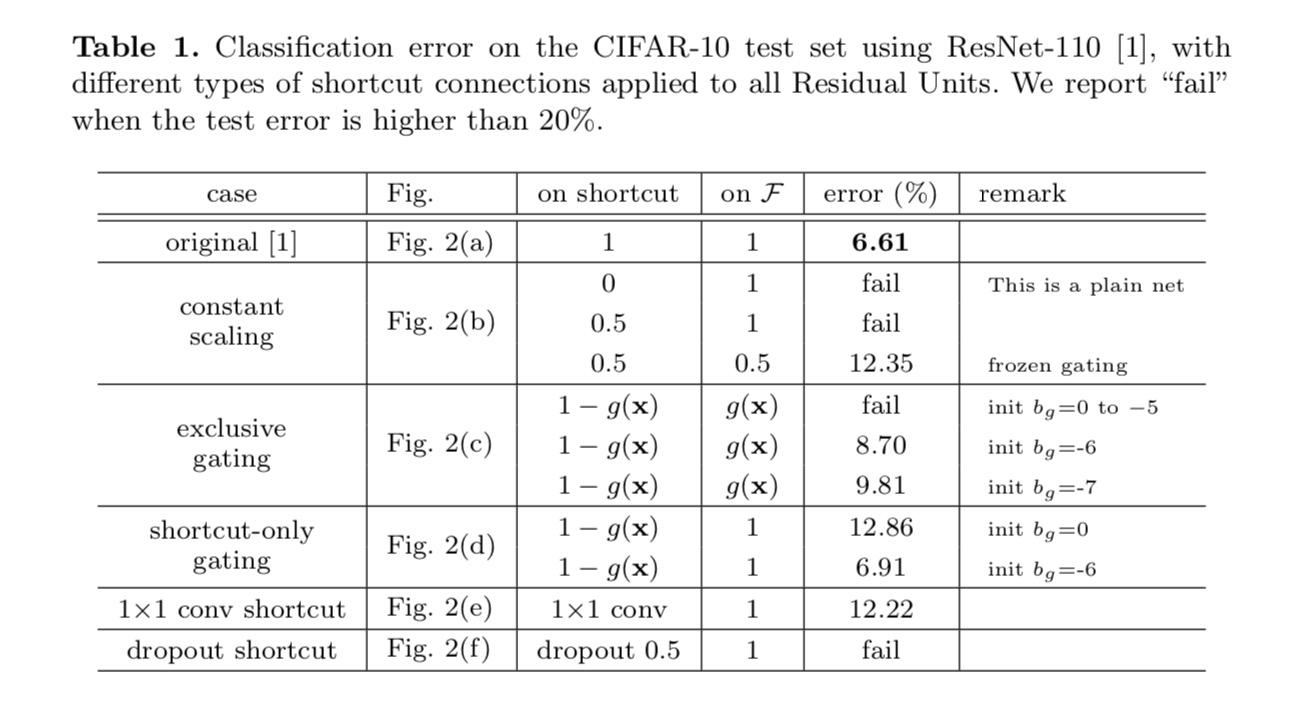
Come indicato dalle frecce in grigio nella figura, il collegamento collegamenti sono i percorsi più diretti per le informazioni di propagare. Le manipolazioni moltiplicative (scaling, gating, circonvoluzioni 1×1 e dropout) sulle scorciatoie possono ostacolare la propagazione delle informazioni e portare a problemi di ottimizzazione.

È interessante notare che le scorciatoie convoluzionali gating e 1×1 introducono più parametri e dovrebbero avere capacità di rappresentazione più forti delle scorciatoie di identità. In effetti, il gating di sola scorciatoia e la convoluzione 1×1 coprono lo spazio della soluzione delle scorciatoie di identità (cioè potrebbero essere ottimizzate come scorciatoie di identità). Tuttavia, il loro errore di formazione è superiore a quello delle scorciatoie di identità, indicando che il degrado di questi modelli è causato da problemi di ottimizzazione, invece di capacità di rappresentazione.

Utilizzo delle funzioni di attivazione

Gli esperimenti nella sezione precedente presuppongono che l’attivazione post-aggiunta sia la mappatura dell’identità. Ma negli esperimenti di cui sopra è ReLU come progettato nel primo documento. Successivamente indaghiamo l’impatto di .

Vogliamo fare una mappatura dell’identità, che viene eseguita riorganizzando le funzioni di attivazione (ReLU e/o BN, normalizzazione batch). Nella figura seguente, l’unità residua originale nell’ultima carta ha una forma in Fig. 4 (a) – BN viene utilizzato dopo ogni strato di peso e ReLU viene adottato dopo BN tranne che l’ultimo ReLU in un’unità residua è dopo l’aggiunta elementwise ( = ReLU). Fico. 4 (b-e) mostra le alternative che abbiamo studiato.

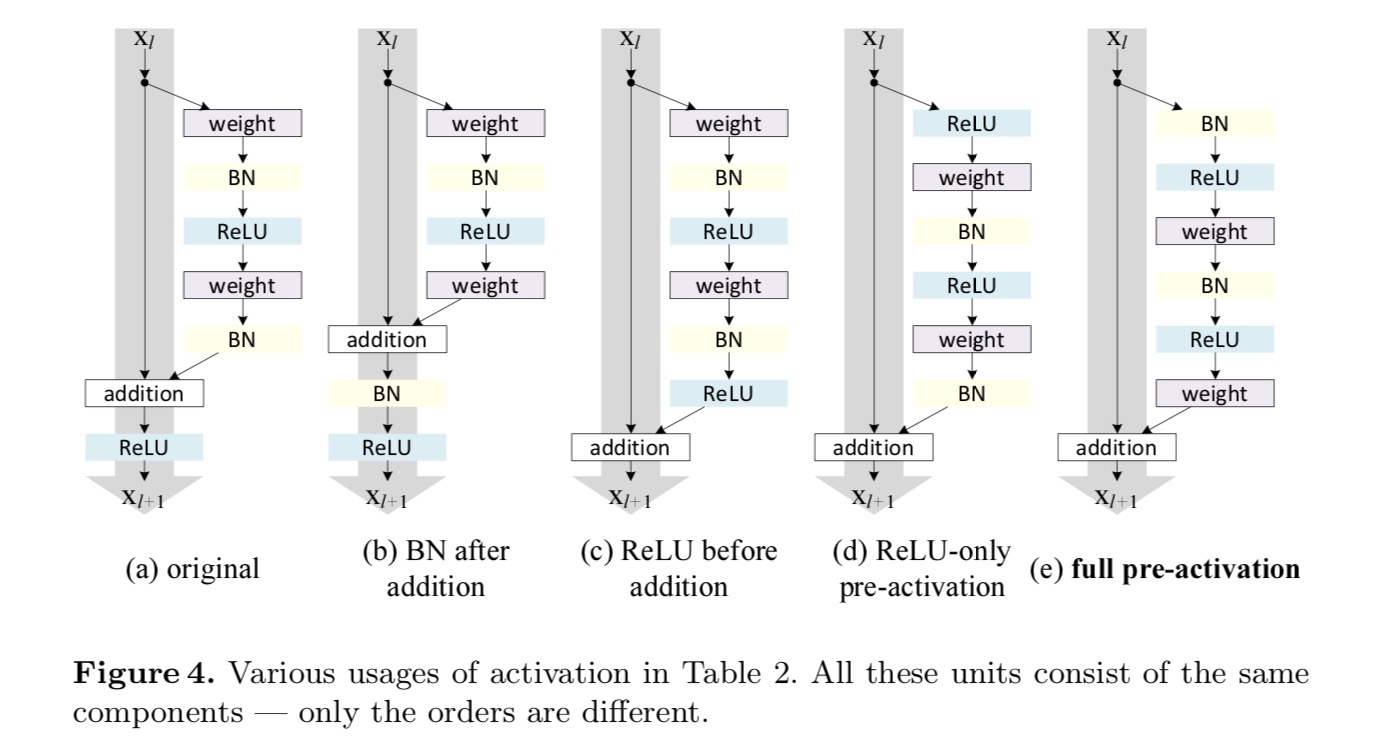
Esperimenti sull’attivazione

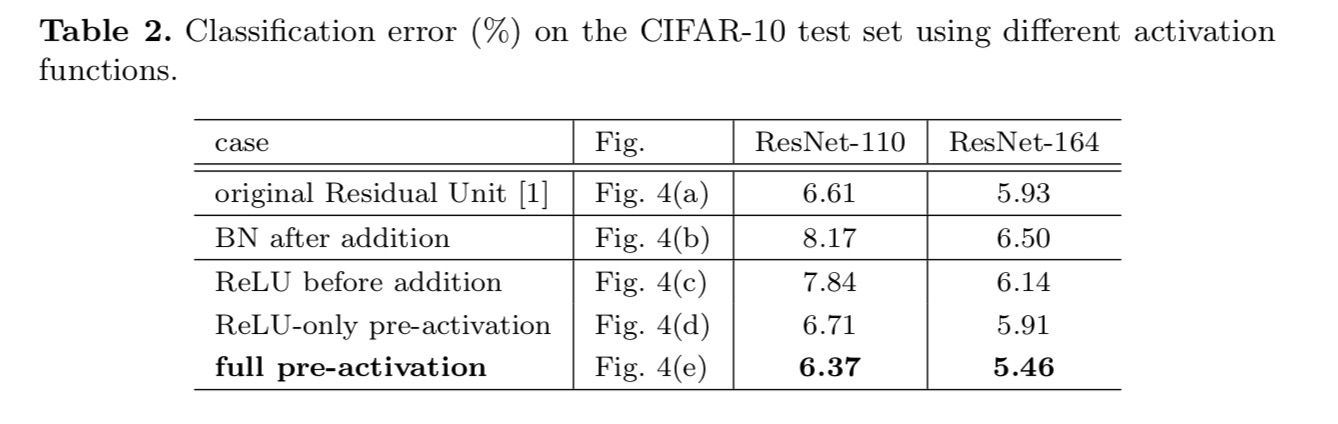
In questa sezione sperimentiamo ResNet-110 e un’architettura a collo di bottiglia a 164 strati (indicata come ResNet-164). Un’unità residua a collo di bottiglia è costituita da uno strato 1×1 per ridurre la dimensione, uno strato 3×3 e uno strato 1×1 per ripristinare la dimensione. Come progettato nell’ultimo documento, la sua complessità computazionale è simile all’unità residua due-3×3.

Post-attivazione o pre-attivazione?

Nel progetto originale, l’attivazione influisce su entrambi i percorsi nell’Unità residua successiva: . Successivamente sviluppiamo una forma asimmetrica in cui un’attivazione influenza solo il percorso:, per qualsiasi . Rinominando le notazioni, abbiamo la seguente forma:

Per questa nuova Unità Residua come nell’equazione precedente, la nuova attivazione dopo l’aggiunta diventa una mappatura dell’identità. Questo disegno significa che se una nuova attivazione post-aggiunta viene adottata asimmetricamente, equivale alla rifusione come pre-attivazione dell’Unità residua successiva. Questo è illustrato nella figura seguente:

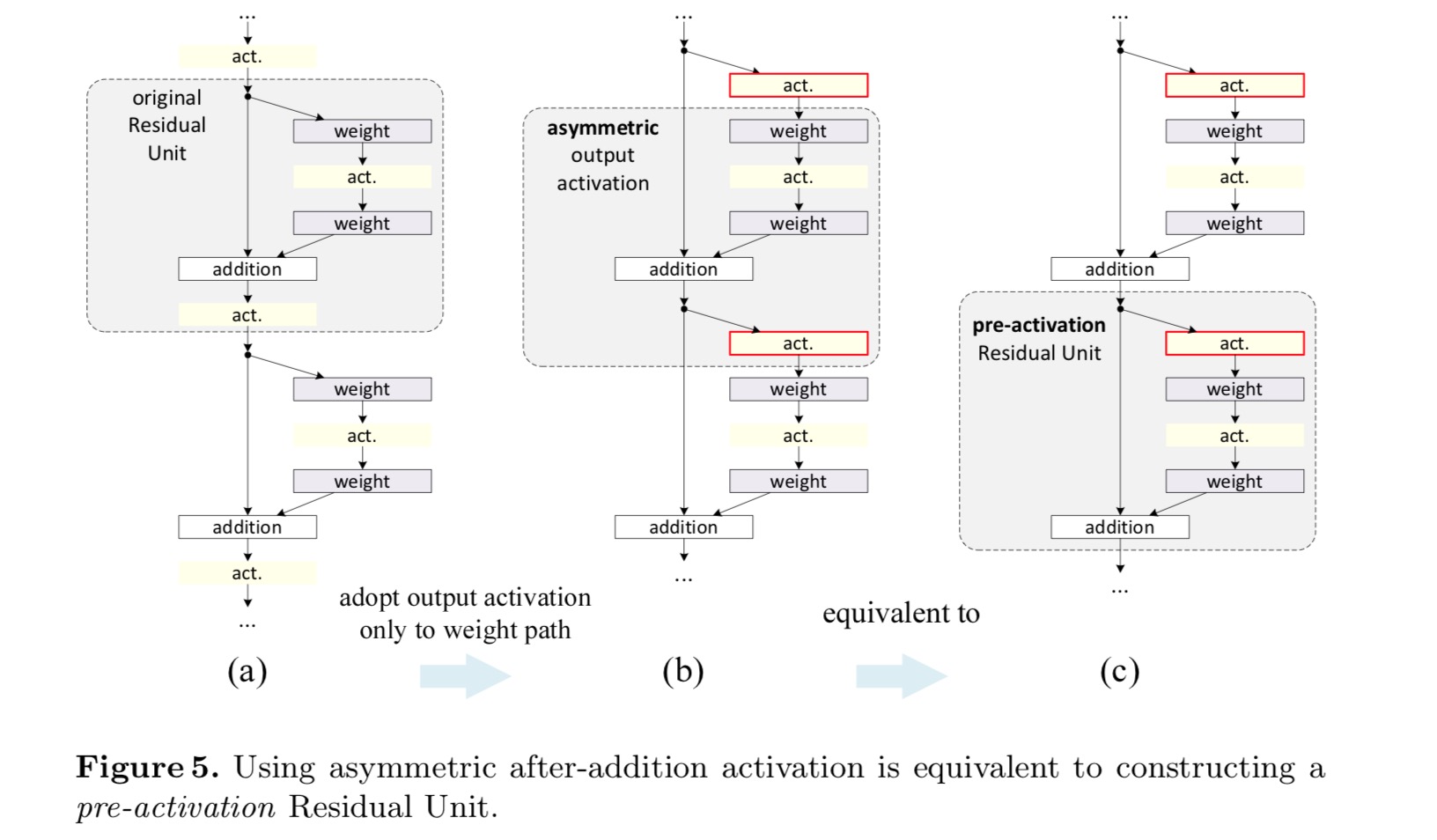
La distinzione tra post-attivazione / pre-attivazione è causata dalla presenza dell’aggiunta di elementi. Per una rete semplice che ha N livelli, ci sono attivazioni N – 1 (BN/ReLU), e non importa se le consideriamo come post-o pre-attivazioni. Ma per i livelli ramificati uniti per aggiunta, la posizione dell’attivazione è importante. I vari usi di attivazione sono visualizzati in Figura 4.

Sperimentiamo con due di questi disegni: (1) Pre-attivazione ReLU-only e (2) pre-attivazione completa in cui BN e ReLU sono entrambi adottati prima degli strati di peso. In qualche modo sorprendentemente, quando BN e ReLU sono entrambi usati come pre-attivazione, i risultati sono migliorati da margini sani

Troviamo che l’impatto della pre-attivazione è duplice. Innanzitutto, l’ottimizzazione viene ulteriormente facilitata (confrontando con la ResNet di base) perché f è una mappatura dell’identità. In secondo luogo, l’utilizzo di BN come pre-attivazione migliora la regolarizzazione dei modelli.

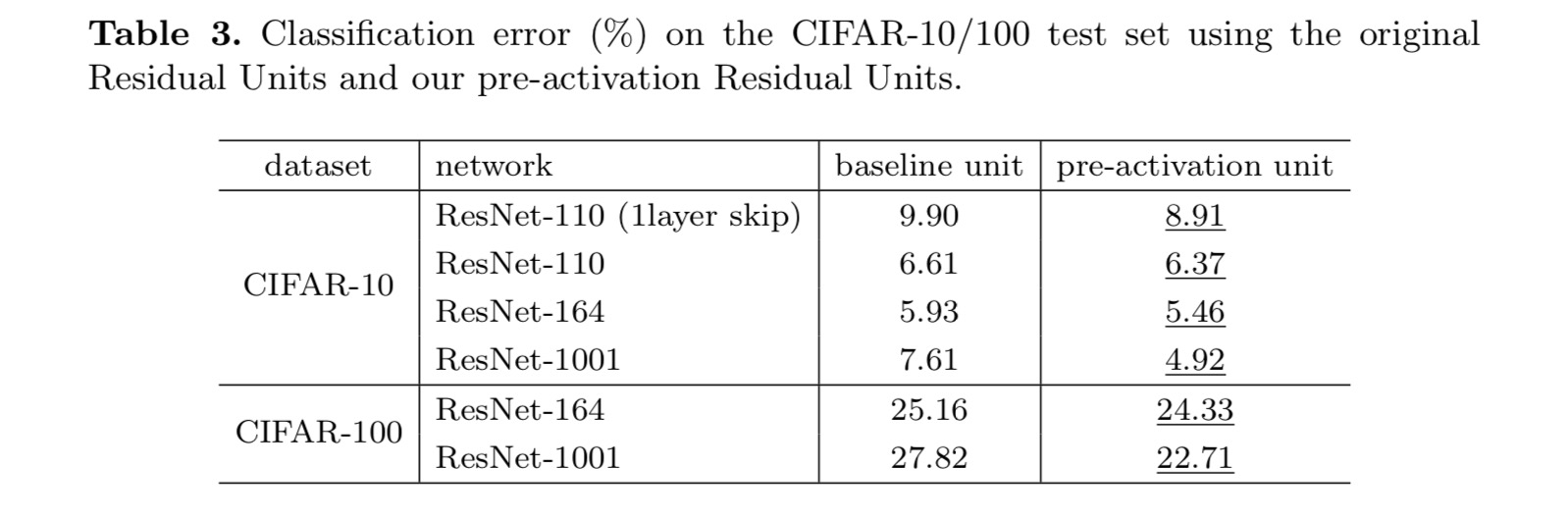
Conclusione

Questo articolo indaga le formulazioni di propagazione dietro i meccanismi di connessione delle reti residue profonde. Le nostre derivazioni implicano che le connessioni scorciatoie di identità e l’attivazione dell’identità dopo l’aggiunta sono essenziali per rendere agevole la propagazione delle informazioni. Gli esperimenti di ablazione dimostrano fenomeni coerenti con le nostre derivazioni. Presentiamo anche reti profonde a 1000 strati che possono essere facilmente addestrate e ottenere una maggiore precisione.

Trasformazione residua aggregata per reti neurali profonde

Introduzione

La ricerca sul riconoscimento visivo sta subendo una transizione da “feature engineering” a “network engineering”. Lo sforzo umano è stato spostato nella progettazione di architetture di rete migliori per l’apprendimento delle rappresentazioni.

Progettare architetture diventa sempre più difficile con il crescente numero di iper-parametri, specialmente quando ci sono molti livelli. Le reti VGG presentano una strategia semplice ma efficace di costruzione di reti molto profonde: impilare blocchi di costruzione della stessa forma. Questa strategia è ereditata da ResNet che impilano moduli della stessa topologia. Questa semplice regola riduce le scelte libere dei parametri iper, e la profondità è esposta come una dimensione essenziale nelle reti neurali. Inoltre, sosteniamo che la semplicità di questa regola può ridurre il rischio di un eccessivo adattamento degli iperparametri a un set di dati specifico. La robustezza delle reti e delle reti VGG è stata dimostrata da varie attività di riconoscimento visivo e da attività non visive che coinvolgono la parola e il linguaggio.

A differenza di VGG-nets, la famiglia di modelli Inception ha dimostrato che topologie accuratamente progettate sono in grado di ottenere una precisione convincente con una bassa complessità teorica. I modelli di Inception si sono evoluti nel tempo, ma un’importante proprietà comune è una strategia split-transform-merge. In un modulo Inception, l’ingresso è diviso in alcuni embeddings di dimensioni inferiori (da 1×1 circonvoluzioni), trasformati da una serie di filtri specializzati (3×3, 5×5, ecc.), e uniti per concatenazione. Si prevede che il comportamento split-transform-merge dei moduli Inception si avvicini alla potenza rappresentativa di strati grandi e densi, ma a una complessità computazionale notevolmente inferiore.

Nonostante una buona accuratezza, la realizzazione dei modelli di Inception è stata accompagnata da una serie di fattori complicanti. Sebbene combinazioni attente di questi componenti producano eccellenti ricette di rete neurale, in generale non è chiaro come adattare le architetture di Inception a nuovi set di dati/attività, specialmente quando ci sono molti fattori e iper-parametri da progettare.

In questo articolo, presentiamo una semplice architettura che adotta la strategia di VGG / ResNet di ripetere i livelli, sfruttando la strategia split-transform-merge in modo facile ed estensibile. Un modulo nella nostra rete esegue un insieme di trasformazioni, ciascuna su un embedding a bassa dimensione, i cui output sono aggregati per somma. Perseguiamo una semplice realizzazione di questa idea — le trasformazioni da aggregare sono tutte della stessa topologia. Questo design ci consente di estendere a qualsiasi numero elevato di trasformazioni senza disegni specializzati.

Dimostriamo empiricamente che le nostre trasformazioni aggregate superano il modulo ResNet originale, anche nella condizione limitata di mantenere la complessità computazionale e la dimensione del modello. Sottolineiamo che mentre è relativamente facile aumentare la precisione aumentando la capacità (andando più in profondità o più ampia), i metodi che aumentano la precisione mantenendo (o riducendo) la complessità sono rari in letteratura.

Il nostro metodo indica che la cardinalità (la dimensione dell’insieme delle trasformazioni) è una dimensione concreta e misurabile che è di importanza centrale, oltre alle dimensioni di larghezza e profondità. Gli esperimenti dimostrano che aumentare la cardinalità è un modo più efficace per ottenere precisione rispetto ad andare più in profondità o più ampio, specialmente quando profondità e larghezza iniziano a dare rendimenti decrescenti per i modelli esistenti.

Le nostre reti neurali, denominate ResNeXt (suggerendo la dimensione successiva), superano ResNet-101/152, ResNet-200, Inception-v3 e Inception-ResNet-v2 sul set di dati di classificazione ImageNet. In particolare, un ResNeXt a 101 strati è in grado di ottenere una precisione migliore rispetto a ResNet-200 ma ha solo il 50% di complessità. Inoltre, ResNeXt presenta disegni notevolmente più semplici rispetto a tutti i modelli Inception.

Metodo

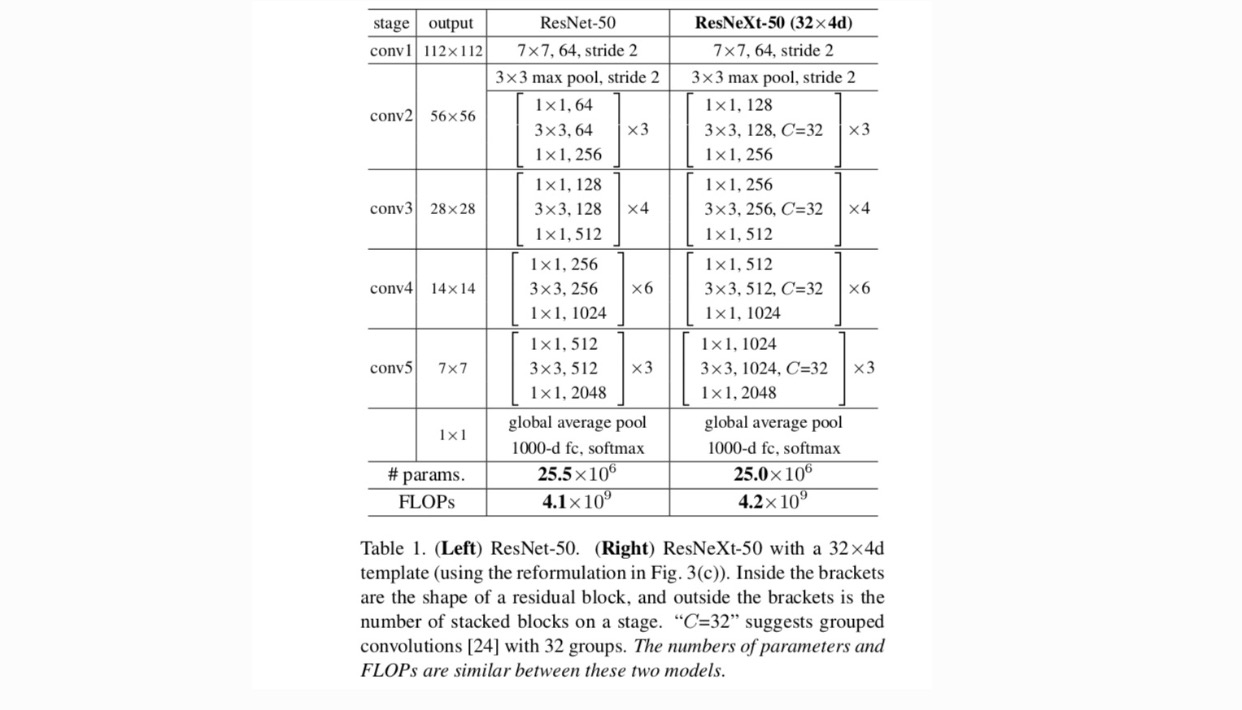
Adottiamo un design altamente modularizzato seguendo VGG / ResNet. La nostra rete è costituita da una pila di blocchi residui. Questi blocchi hanno la stessa topologia, e sono soggetti a due semplici regole ispirate VGG/ResNets: (1) se la produzione di mappe spaziali della stessa dimensione, i blocchi condividono la stessa hyper-parametri (larghezza e dimensioni del filtro), e (2) ogni volta che la mappa spaziale è il downsampling di un fattore 2, la larghezza dei blocchi è moltiplicato per un fattore 2. La seconda regola assicura che la complessità computazionale, in termini di FLOP (operazioni in virgola mobile, in #di moltiplicare-aggiunge), sia approssimativamente la stessa per tutti i blocchi.

Con queste due regole, abbiamo solo bisogno di progettare un modulo modello e tutti i moduli in una rete possono essere determinati di conseguenza. Quindi queste due regole restringono notevolmente lo spazio di progettazione e ci permettono di concentrarci su alcuni fattori chiave. Le reti costruite da queste regole sono nella tabella 1.

I neuroni più semplici nelle reti neurali artificiali eseguono il prodotto interno (somma ponderata), che è la trasformazione elementare eseguita da strati completamente connessi e convoluzionali.

L’operazione di cui sopra può essere rifusa come combinazione di suddivisione, trasformazione e aggregazione. (1): Splitting: il vettore viene affettato come un embedding a bassa dimensione, e in quanto sopra, è un sottospazio a singola dimensione (2) Transforming: la rappresentazione a bassa dimensione viene trasformata, e in quanto sopra, viene semplicemente ridimensionata: (3) Aggregating: le trasformazioni in tutti gli embeddings sono aggregate da .

Data l’analisi di cui sopra di un neurone semplice, consideriamo la sostituzione della trasformazione elementare (w_i, x_i) con una funzione più generica, che di per sé può anche essere una rete. Formalmente, presentiamo trasformazioni aggregate come:

dove può essere una funzione arbitraria. Analogo a un semplice neurone, dovrebbe proiettarsi in un embedding (opzionalmente a bassa dimensione) e quindi trasformarlo.

Ci riferiamo alla cardinalità. è in una posizione simile a in, ma non deve essere uguale e può essere un numero arbitrario. Mostriamo con esperimenti che la cardinalità è una dimensione essenziale e può essere più efficace delle dimensioni di larghezza e profondità.

In questo articolo, consideriamo un modo semplice di progettare le funzioni di trasformazione: tutte hanno la stessa topologia. Questo estende la strategia in stile VGG di ripetere strati della stessa forma. Abbiamo impostato la trasformazione individuale per essere l’architettura a forma di collo di bottiglia illustrata in Fig. 1 (a destra). In questo caso, il primo strato 1×1 in ciascuno produce l’incorporamento a bassa dimensione.

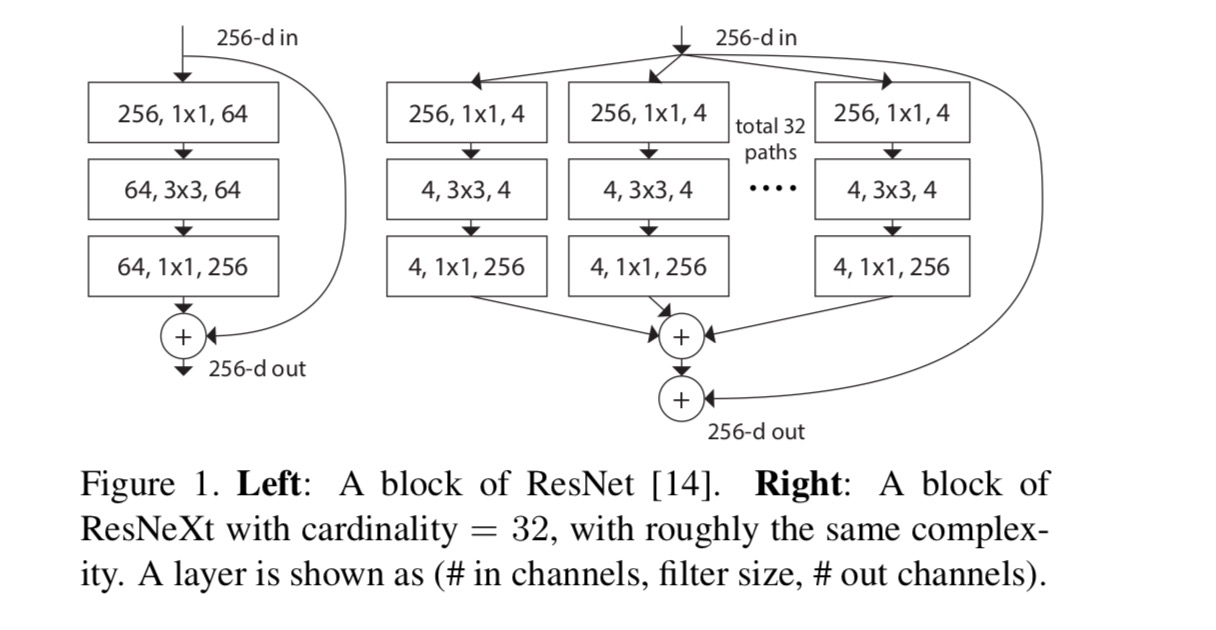
La trasformazione aggregata nell’ultima equazione serve come funzione residua:

dove è l’output.

Le relazioni tra ResNeXt e Inception-ResNet / Grouped-Circonvolutions sono mostrate nella figura seguente:

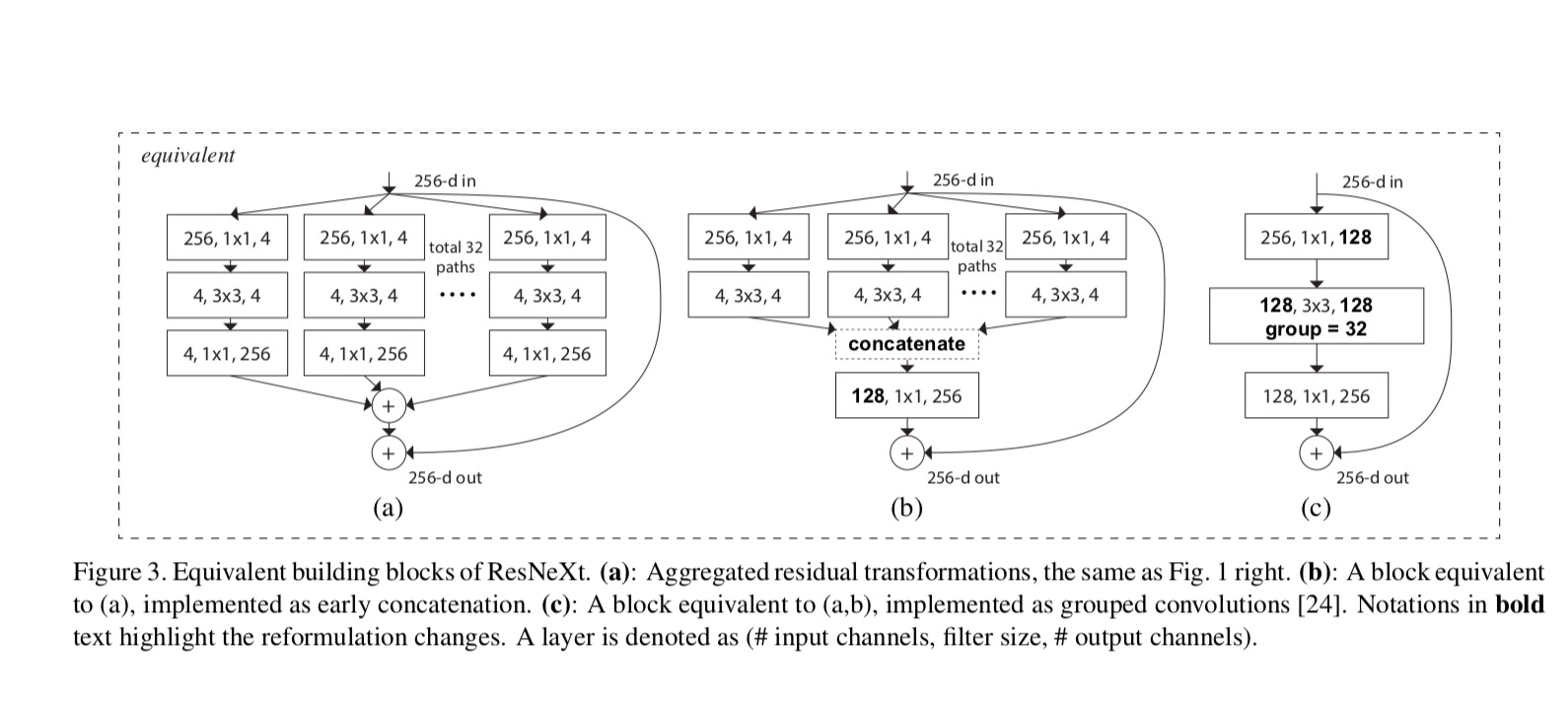
Quando valutiamo diverse cardinalità preservando la complessità, vogliamo ridurre al minimo la modifica di altri iper-parametri. Scegliamo di regolare la larghezza del collo di bottiglia (ad esempio, 4-d in Fig 1(a destra)), perché può essere isolato dall’ingresso e dall’uscita del blocco. Questa strategia non introduce modifiche ad altri iper-parametri (profondità o larghezza di input/output dei blocchi), quindi è utile per noi concentrarci sull’impatto della cardinalità.

In Fig. 1 (a sinistra), il blocco di collo di bottiglia ResNet originale ha parametri e FLOP proporzionali (sulla stessa dimensione della mappa delle funzionalità). Con larghezza collo di bottiglia, il nostro modello in Fig. 1 (a destra) ha: parametri e FLOP proporzionali. Quando e, questo numero . La tabella seguente mostra la relazione tra cardinalità e larghezza del collo di bottiglia .

Esperimenti

Cardinalità rispetto alla larghezza. Valutiamo innanzitutto il trade-off tra cardinalità e larghezza del collo di bottiglia, sotto la complessità preservata come elencato nella Tabella 2. La tabella 3 mostra i risultati. Confrontando con ResNet-50, il 32×4d ResNeXt-50 ha un errore di convalida del 22,2%, che è inferiore dell ‘ 1,7% rispetto al 23,9% della linea di base ResNet. Con la cardinalità che aumenta da 1 a 32 mantenendo la complessità, il tasso di errore continua a diminuire. Inoltre, il 32×4d ResNeXt ha anche un errore di allenamento molto più basso rispetto al ResNet countetpart, suggerendo che i guadagni non derivano dalla regolarizzazione ma da rappresentazioni più forti.

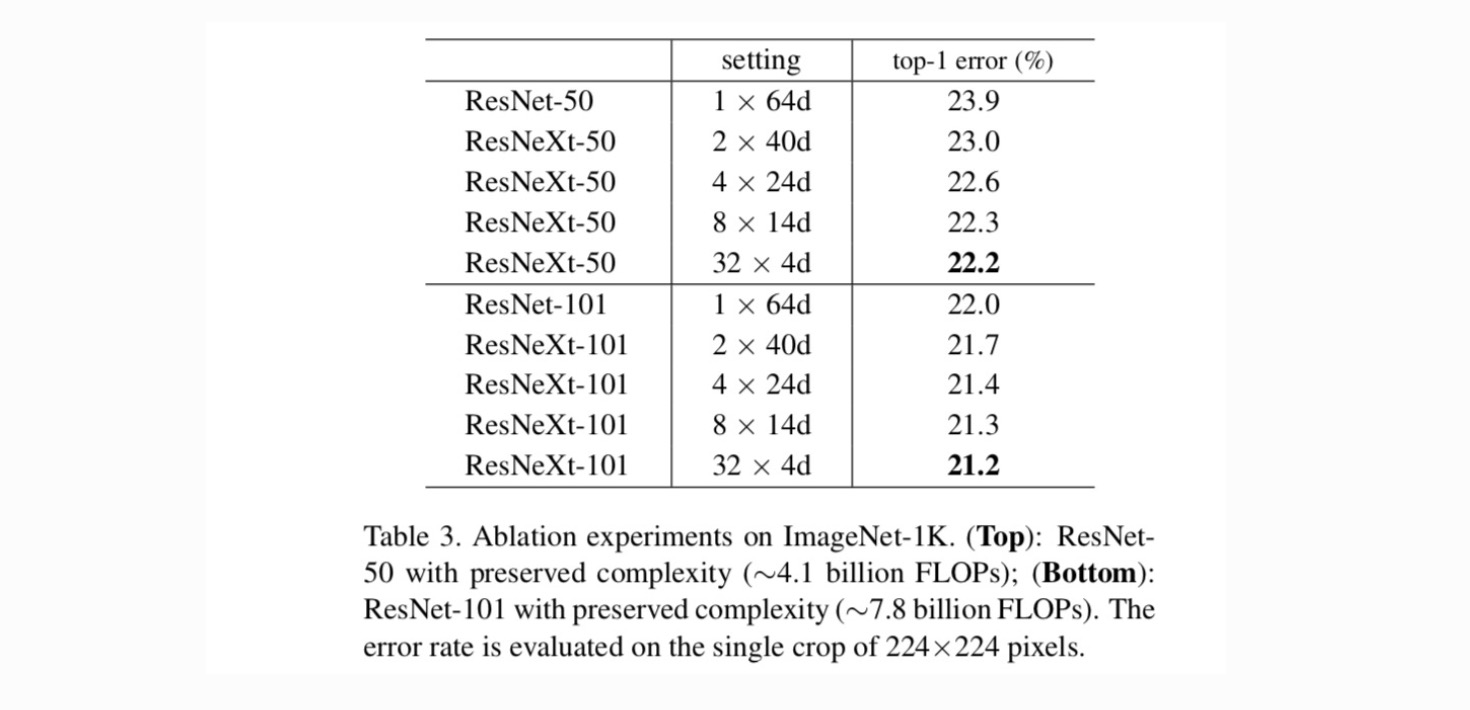
Aumentare la cardinalità rispetto a più profondo / più ampio.

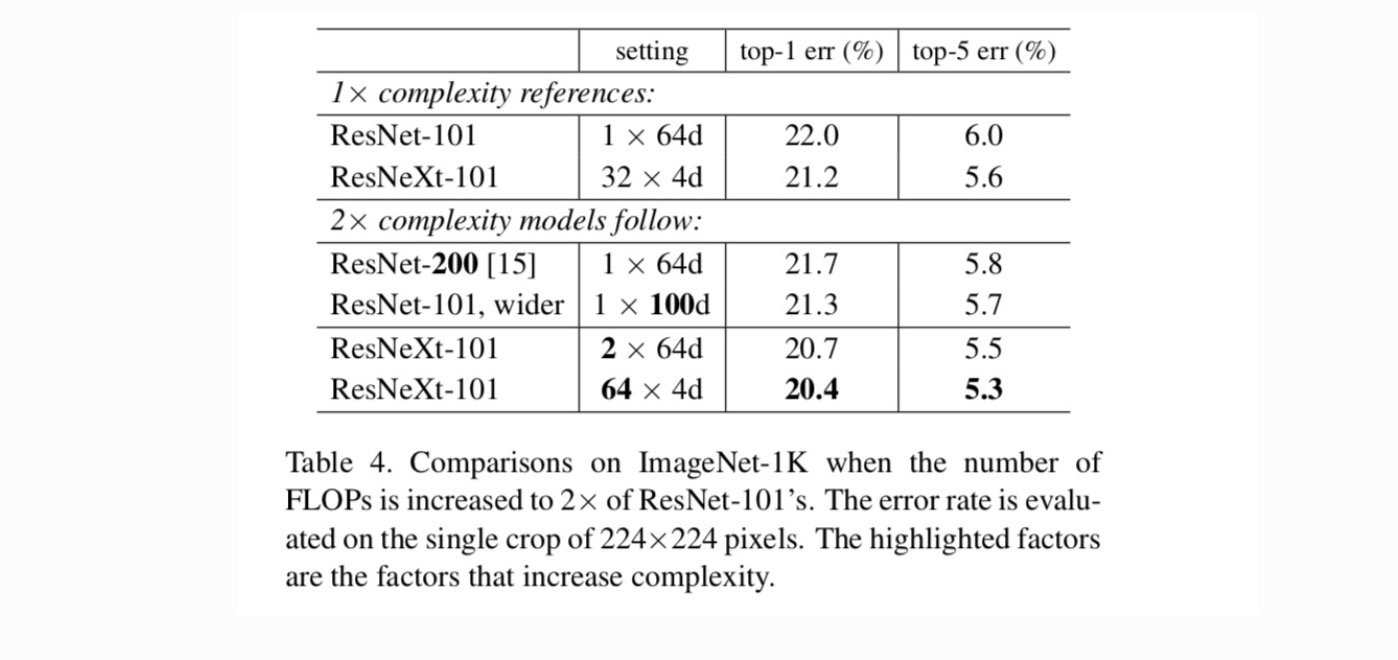
Successivamente indaghiamo la crescente complessità aumentando la cardinalità C o aumentando la profondità o la larghezza. Confrontiamo le seguenti varianti (1) Andando più in profondità a 200 strati. Adottiamo il ResNet-200. (2) Andando più ampio aumentando la larghezza del collo di bottiglia. (3) Aumentare la cardinalità raddoppiando C.

La Tabella 4 mostra che l’aumento della complessità di 2× riduce costantemente l’errore rispetto alla linea di base ResNet-101 (22,0%). Ma il miglioramento è piccolo quando si va più in profondità (ResNet-200, dello 0,3%) o più ampio (ResNet-101 più ampio, dello 0,7%). Al contrario, aumentare la cardinalità C mostra risultati molto migliori rispetto ad andare più in profondità o più in largo.

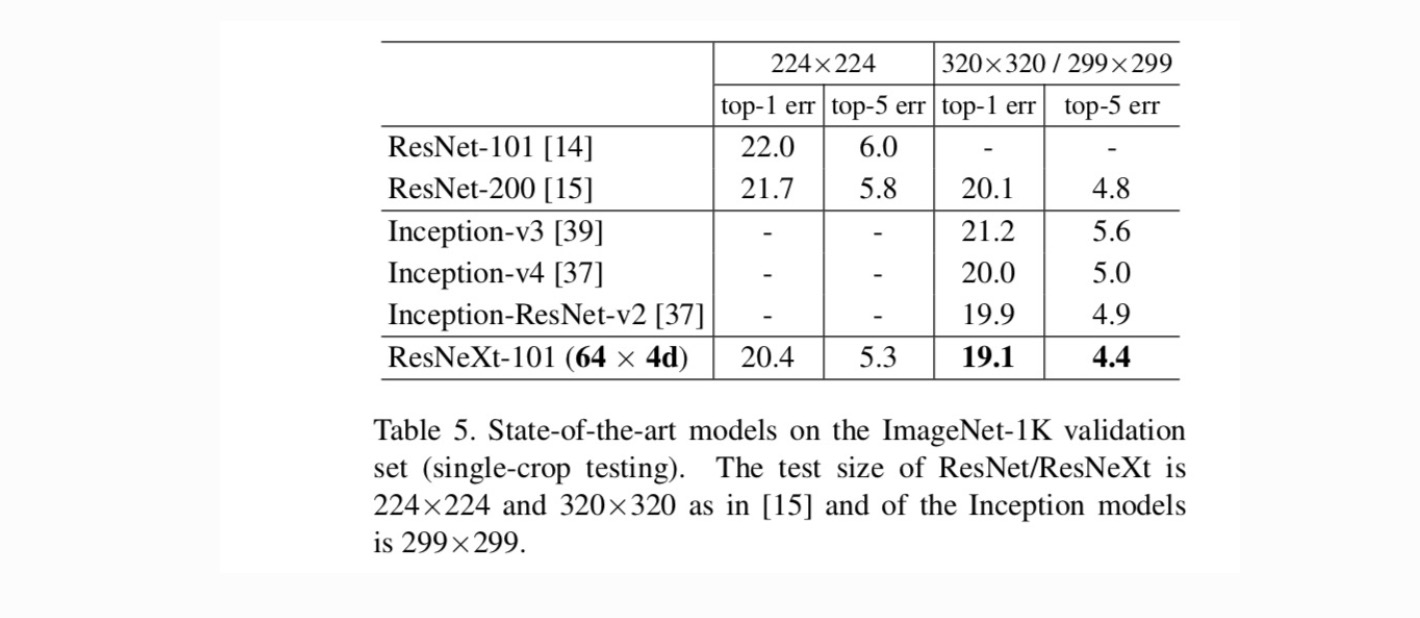
Confronti con risultati all’avanguardia. La tabella 5 mostra ulteriori risultati dei test a coltura singola sul set di convalida ImageNet. I nostri risultati si confrontano favorevolmente con ResNet, Inception-v3 / v4 e Inception-ResNet-v2, raggiungendo un tasso di errore top-5 a coltura singola del 4,4%. Inoltre, la nostra progettazione architettonica è molto più semplice di tutti i modelli Inception e richiede un numero notevolmente inferiore di iper-parametri da impostare a mano.