Introduzione
Principal Components Analysis (PCA) è un algoritmo di riduzione dimensionalità che può essere utilizzato per accelerare in modo significativo il vostro algoritmo di apprendimento caratteristica senza supervisione. Ancora più importante, comprendere PCA ci consentirà di implementare in seguito lo sbiancamento, che è un importante passo di pre-elaborazione per molti algoritmi.
Supponiamo che tu stia allenando il tuo algoritmo sulle immagini. Quindi l’input sarà in qualche modo ridondante, perché i valori dei pixel adiacenti in un’immagine sono altamente correlati. Concretamente, supponiamo che ci stiamo allenando su patch di immagini in scala di grigi 16×16. Quindi \ textstyle x \ in \ Re^{256} sono 256 vettori dimensionali, con una caratteristica \ textstyle x_j corrispondente all’intensità di ciascun pixel. A causa della correlazione tra pixel adiacenti, PCA ci permetterà di approssimare l’input con uno dimensionale molto più basso, incorrendo in un errore molto piccolo.
Esempio e background matematico
Per il nostro esempio in esecuzione, useremo un set di dati \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} con \textstyle n=2 input dimensionali, in modo che \textstyle x^{(i)} \in \Re^2. Supponiamo di voler ridurre i dati da 2 dimensioni a 1. (In pratica, potremmo voler ridurre i dati da 256 a 50 dimensioni, ad esempio; ma l’utilizzo di dati dimensionali inferiori nel nostro esempio ci consente di visualizzare meglio gli algoritmi.) Ecco il nostro set di dati:
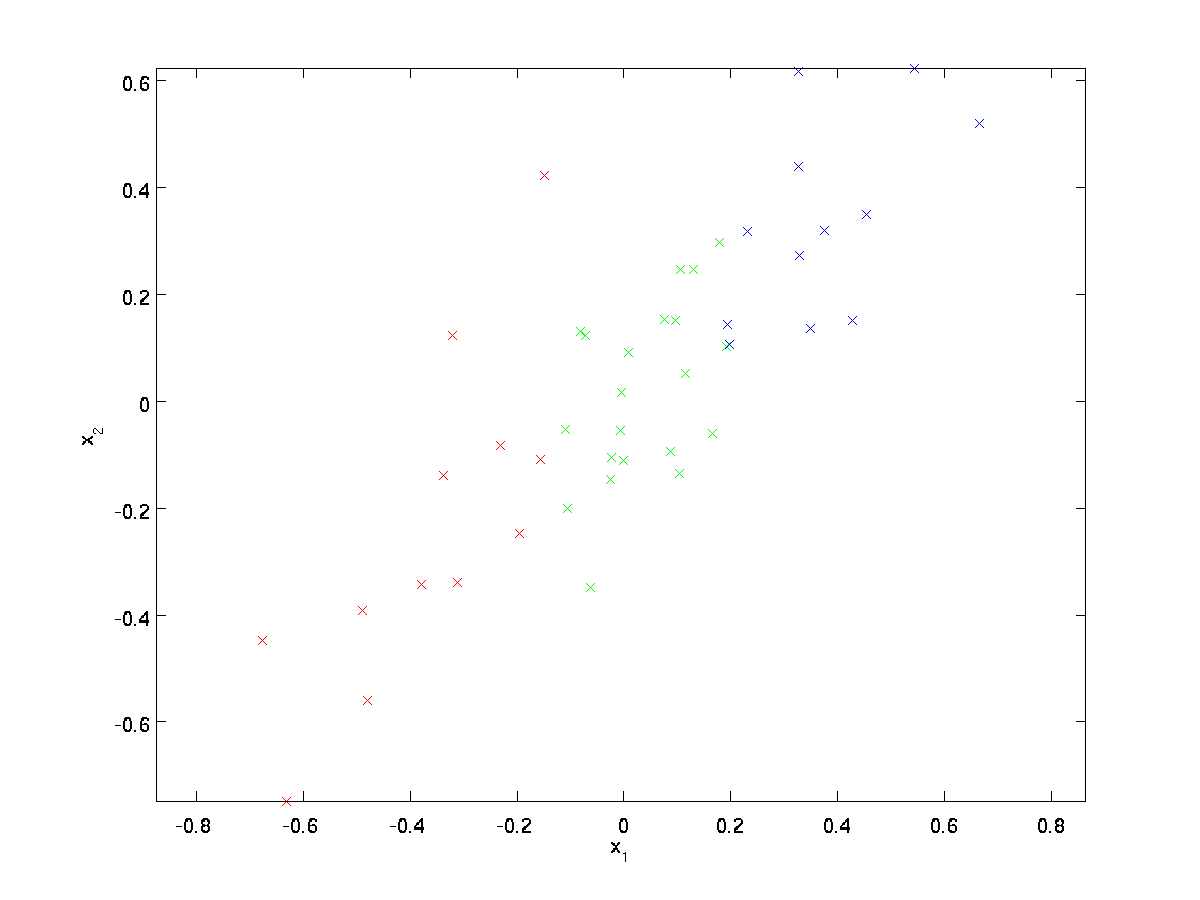
Questi dati sono già stati pre-elaborati in modo che ciascuna delle funzionalità \textstyle x_1 e \textstyle x_2 abbia circa la stessa media (zero) e varianza.
Ai fini dell’illustrazione, abbiamo anche colorato ciascuno dei punti uno dei tre colori, a seconda del loro valore \ textstyle x_1; questi colori non vengono utilizzati dall’algoritmo e sono solo a scopo illustrativo.
PCA troverà un sottospazio dimensionale inferiore su cui proiettare i nostri dati.
Dall’esame visivo dei dati, sembra che \textstyle u_1 sia la direzione principale di variazione dei dati e \textstyle u_2 la direzione secondaria di variazione:
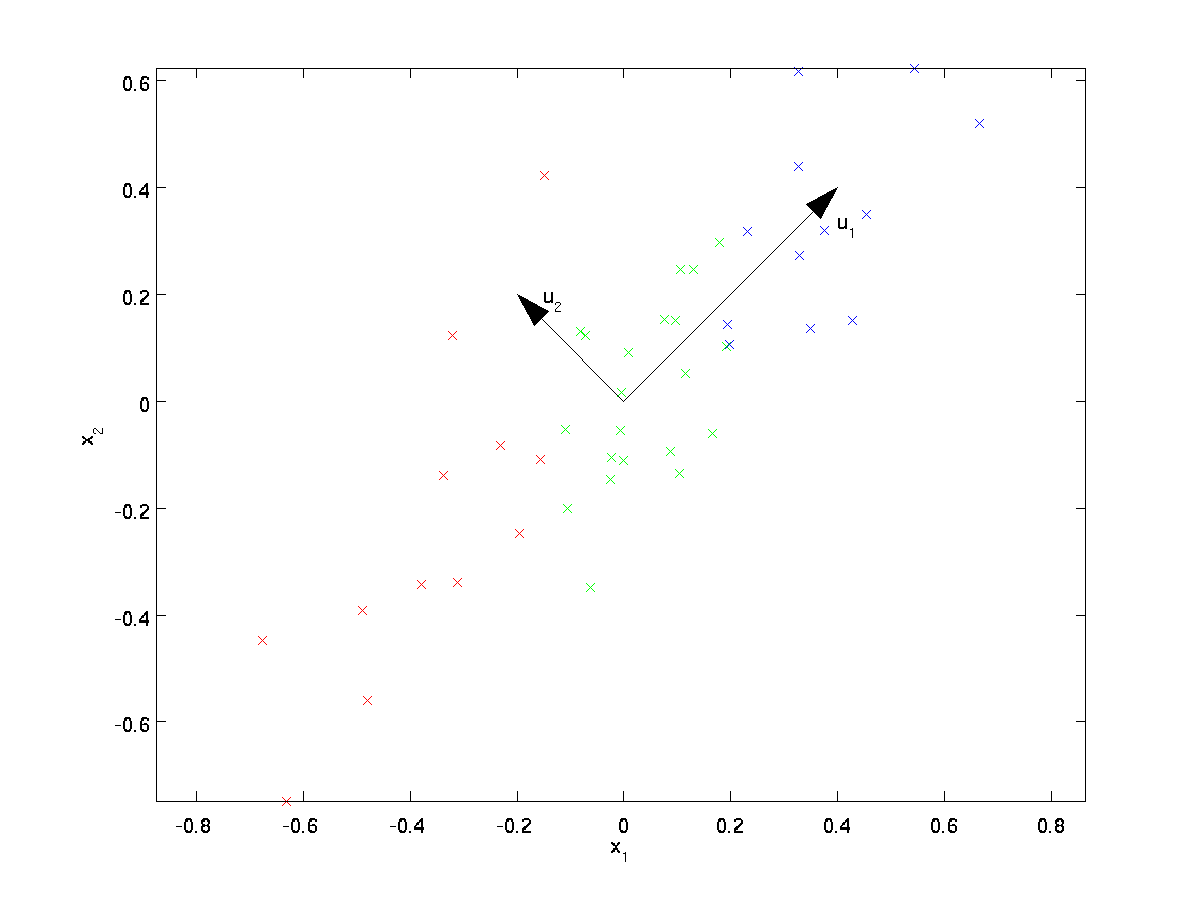
Cioè, i dati variano molto di più nella direzione \textstyle u_1 rispetto a \textstyle u_2. Per trovare più formalmente le direzioni \ textstyle u_1 e \ textstyle u_2, calcoliamo prima la matrice \ textstyle \ Sigma come segue:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}
Se \textstyle x ha media uguale a zero, quindi \textstyle \Sigma è esattamente la matrice di covarianza \textstyle x. (Il simbolo “\textstyle \Sigma”, pronunciato “Sigma”, è la notazione standard per indicare la matrice di covarianza. Sfortunatamente sembra proprio il simbolo di somma, come in \sum_{i=1}^n i; ma queste sono due cose diverse.)
Si può quindi dimostrare che \textstyle u_1—la direzione principale di variazione dei dati—è l’autovettore superiore (principale) di \textstyle \Sigma, e \textstyle u_2 è il secondo autovettore.
Nota: Se sei interessato a vedere una derivazione matematica/giustificazione più formale di questo risultato, vedi le note di lezione CS229 (Machine Learning) su PCA (link in fondo a questa pagina). Non sarà necessario farlo per seguire questo corso, tuttavia.
È possibile utilizzare il software di algebra lineare numerica standard per trovare questi autovettori (vedere Note di implementazione). Concretamente, calcoliamo gli autovettori di \ textstyle \ Sigma e impiliamo gli autovettori in colonne per formare la matrice \ textstyle U:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
I vettori \textstyle u_1 e \textstyle u_2 nel nostro esempio formano una nuova base in cui possiamo rappresentare i dati. Concretamente, lascia che \ textstyle x \ in \ Re^2 sia un esempio di allenamento. Quindi \ textstyle u_1 ^ Tx è la lunghezza (grandezza) della proiezione di \textstyle x sul vettore \textstyle u_1.
Allo stesso modo, \textstyle u_2^Tx è la grandezza di \textstyle x proiettata sul vettore \textstyle u_2.
Rotazione di Dati
Così, siamo in grado di rappresentare \textstyle x il \textstyle (u_1, u_2)-base di calcolo
\begin{align}x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}
(Il pedice “rot” nasce dall’osservazione che questo corrisponde a una rotazione (e, possibilmente, di riflessione) dei dati originali.) Prendiamo l’intero set di allenamento e calcoliamo \ textstyle x_ {\rm rot}^{(i)} = U^Tx ^ {(i)} per ogni \ textstyle i. Tracciando questi dati trasformati \ textstyle x_ {\rm rot}, otteniamo:

Questo è il set di allenamento ruotato nella base \textstyle u_1,\textstyle u_2. Nel caso generale, \ textstyle U ^ Tx sarà il set di allenamento ruotato nella base \ textstyle u_1, \ textstyle u_2,…, \textstyle u_n.
Una delle proprietà di \textstyle U è che si tratta di una matrice “ortogonale”, il che significa che soddisfa \textstyle U^TU = UU^T = I. Quindi, se mai bisogno di andare dal ruotato vettori \textstyle x_{\rm rot} dati originale \textstyle x, è possibile calcolare
\begin{align}x = U x_{\rm rot} ,\end{align}
perché \textstyle U x_{\rm rot} = UU^T x = x.
Ridurre la Dimensione Dati
Si vede che la direzione principale di variazione dei dati è la prima dimensione \textstyle x_{\rm rot,1} di questo ruotato di dati. Quindi, se vogliamo ridurre questi dati a una dimensione, possiamo impostare
\begin{align}\tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re.\end{align}
Più in generale, se \textstyle x \in \Re^n e vogliamo ridurre a un \textstyle k dimensionale rappresentazione \textstyle \tilde{x} \in \Re^k (dove k < n), abbiamo preso il primo \textstyle k componenti di \textstyle x_{\rm rot}, che corrispondono al top \textstyle k indicazioni di variazione.
Un altro modo di spiegare PCA è che \textstyle x_{\rm rot} è un vettore dimensionale \textstyle n, in cui è probabile che i primi componenti siano grandi (ad esempio, nel nostro esempio, abbiamo visto che \ textstyle x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} prende valori ragionevolmente grandi per la maggior parte degli esempi \textstyle i), e i componenti successivi sono probabilmente piccoli (ad esempio, nel nostro esempio, \textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)} era più probabile che fossero piccoli). Quale PCA fa cadere i componenti successivi (più piccoli) di \textstyle x_{\rm rot}, e li approssima semplicemente con 0. Concretamente, la nostra definizione di \textstyle \tilde{x} può anche essere raggiunta usando un’approssimazione a \textstyle x_{\rm rot} dove tutti tranne i primi componenti \textstyle k sono zeri. In altre parole, abbiamo:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{align}
Nel nostro esempio, questo ci dà la seguente trama di \textstyle \tilde{x} (utilizzando \textstyle n=2, k=1):

Tuttavia, poiché i componenti finali \textstyle nk di \textstyle \tilde{x} come definito sopra sarebbero sempre zero, non è necessario mantenere questi zeri intorno, e quindi definiamo \textstyle \tilde{x} come un vettore \textstyle k-dimensionale con solo i primi componenti \textstyle k (diversi da zero).
Questo spiega anche perché volevamo esprimere i nostri dati nella base \textstyle u_1, u_2, \ldots, u_n: decidere quali componenti mantenere diventa solo mantenere i componenti top \textstyle k. Quando lo facciamo, diciamo anche che stiamo ” mantenendo i componenti top \textstyle k PCA (o principal).”
il Recupero di un’Approssimazione dei Dati
Ora, \textstyle \tilde{x} \in \Re^k è un basso-dimensionali, “compresso” rappresentazione dell’originale \textstyle x \in \Re^n. Dato \textstyle \tilde{x} come possiamo recuperare un’approssimazione \textstyle \hat{x} il valore originale di \textstyle x? Da una sezione precedente, sappiamo che \ textstyle x = U x_ {\rm rot}. Inoltre, possiamo pensare a \ textstyle \ tilde {x} come un’approssimazione a \ textstyle x_ {\rm rot}, dove abbiamo impostato gli ultimi componenti \ textstyle nk su zeri. Così, dato \textstyle \tilde{x} \in \Re^k, possiamo pad con \textstyle n-k zeri per ottenere il nostro approssimazione \textstyle x_{\rm rot} \in \Re^n. Infine, abbiamo pre-moltiplicare per \textstyle U per ottenere la nostra approssimazione \textstyle x. Concretamente, abbiamo
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}di 1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \ end {align}
L’uguaglianza finale sopra viene dalla definizione di \textstyle U data in precedenza. (In un’implementazione pratica, in realtà non azzereremmo pad \ textstyle \ tilde{x} e quindi moltiplicheremo per \ textstyle U, poiché ciò significherebbe moltiplicare molte cose per zeri; invece, moltiplicheremo solo \ textstyle \ tilde{x} \ in \ Re ^ k con le prime colonne \ textstyle k di \ textstyle U come nell’espressione finale sopra.) Applicando questo al nostro set di dati, otteniamo la seguente trama per \ textstyle \ hat{x}:
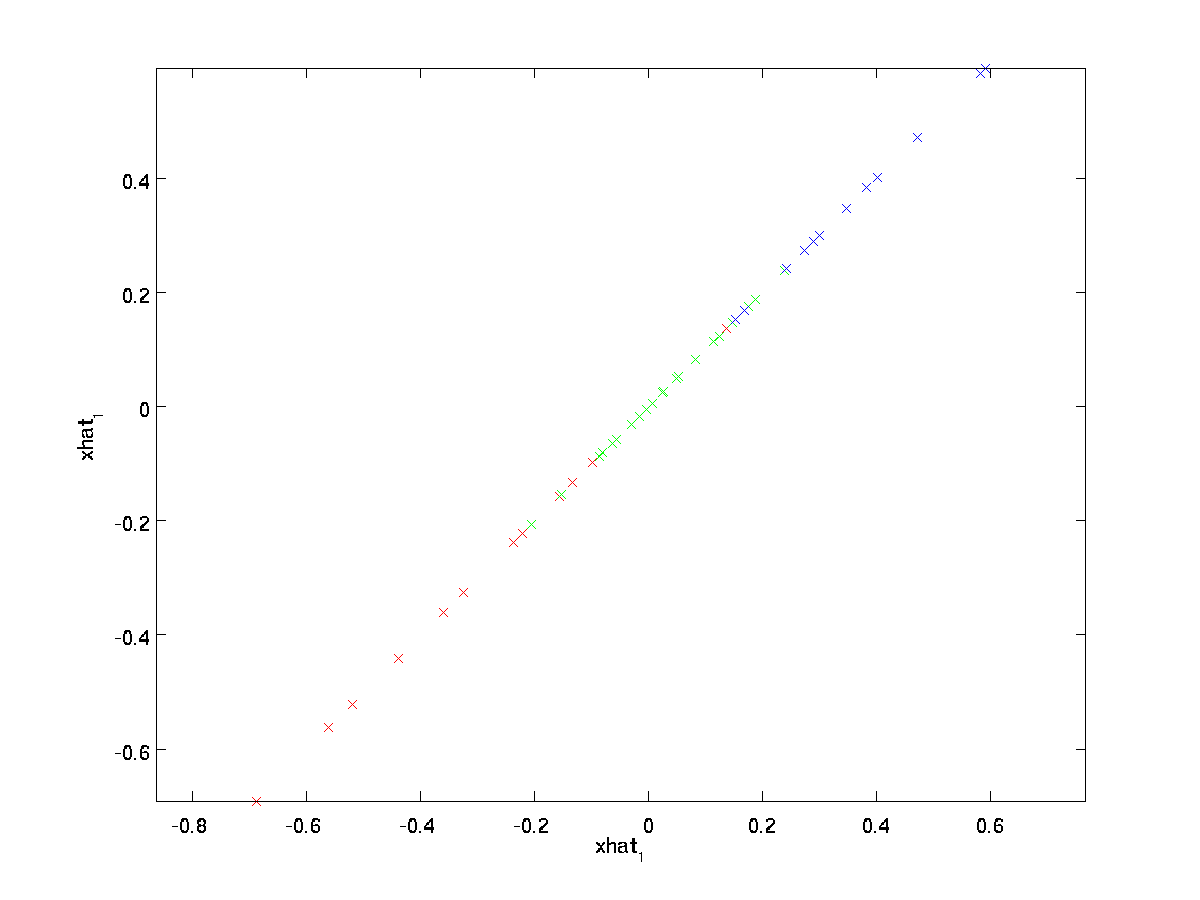
Stiamo quindi utilizzando un’approssimazione dimensionale 1 al set di dati originale.
Se stai allenando un autoencoder o un altro algoritmo di apprendimento delle funzionalità non supervisionato, il tempo di esecuzione del tuo algoritmo dipenderà dalla dimensione dell’input. Se inserisci \ textstyle \ tilde {x} \in \ Re^k nel tuo algoritmo di apprendimento invece di \ textstyle x, ti allenerai su un input dimensionale inferiore e quindi il tuo algoritmo potrebbe funzionare significativamente più velocemente. Per molti set di dati, la rappresentazione dimensionale inferiore \textstyle \tilde{x} può essere un’approssimazione estremamente buona all’originale e l’utilizzo di PCA in questo modo può accelerare significativamente l’algoritmo introducendo un errore di approssimazione molto piccolo.
Numero di componenti da conservare
Come impostiamo \textstyle k; cioè, quanti componenti PCA dovremmo conservare? Nel nostro semplice esempio dimensionale 2, sembrava naturale mantenere 1 dei 2 componenti, ma per dati dimensionali più elevati, questa decisione è meno banale. Se \ textstyle k è troppo grande, non comprimeremo molto i dati; nel limite di \textstyle k=n, quindi stiamo solo usando i dati originali (ma ruotati in una base diversa). Al contrario, se \ textstyle k è troppo piccolo, allora potremmo usare un’approssimazione molto cattiva ai dati.
Per decidere come impostare \textstyle k, di solito guardiamo la “‘percentuale di varianza mantenuta”‘ per diversi valori di \textstyle k. Concretamente, se \textstyle k=n, allora abbiamo un’approssimazione esatta ai dati, e diciamo che il 100% della varianza viene mantenuto. Cioè., tutta la variazione dei dati originali è conservata. Al contrario, se \ textstyle k = 0, allora stiamo approssimando tutti i dati con il vettore zero, e quindi lo 0% della varianza viene mantenuto.
Più in generale, let \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n essere autovalori di \textstyle \Sigma (ordinati in ordine decrescente, in modo che il \textstyle \lambda_j è l’autovalore corrispondente all’autovettore \textstyle u_j. Poi se vogliamo mantenere il \textstyle k componenti principali, la percentuale di varianza conservato è dato da:
\begin{align}\frac {\sum_{j=1}^k\lambda_j} {\sum_{j=1}^n \ lambda_j}.\ end {align}
Nel nostro semplice esempio 2D sopra, \textstyle \lambda_1 = 7.29 e \textstyle \lambda_2 = 0.69. Pertanto, mantenendo solo \ textstyle k=1 componenti principali, abbiamo mantenuto \ textstyle 7.29/(7.29+0.69) = 0.913, o il 91,3% della varianza.
Una definizione più formale di percentuale di varianza mantenuta è al di là dello scopo di queste note. Tuttavia, è possibile mostrare che \ textstyle \ lambda_j = \ sum_{i=1}^m x_ {\rm rot, j}^2. Quindi, se \ textstyle \ lambda_j \ approx 0, questo mostra che \ textstyle x_ {\rm rot, j} di solito è vicino a 0 comunque, e perdiamo relativamente poco approssimandolo con una costante 0. Questo spiega anche perché manteniamo i componenti principali principali (corrispondenti ai valori più grandi di \ textstyle \ lambda_j) invece di quelli inferiori. I componenti principali principali \ textstyle x_ {\rm rot, j} sono quelli che sono più variabili e che assumono valori più grandi, e per i quali incorreremmo in un errore di approssimazione maggiore se li impostassimo a zero.
Nel caso delle immagini, un’euristica comune è scegliere \textstyle k in modo da mantenere il 99% della varianza. In altre parole, selezioniamo il valore più piccolo di \ textstyle k che soddisfa
\begin{align}\frac {\sum_{j=1}^k\lambda_j} {\sum_{j=1}^n \lambda_j} \ geq 0.99. \ end{align}
A seconda dell’applicazione, se si è disposti a incorrere in qualche errore aggiuntivo, vengono talvolta utilizzati anche valori nell’intervallo 90-98%. Quando descrivi agli altri come hai applicato PCA, dicendo che hai scelto \ textstyle k per mantenere il 95% della varianza sarà anche una descrizione molto più facilmente interpretabile che dire che hai mantenuto 120 (o qualsiasi altro numero di) componenti.
PCA sulle immagini
Affinché PCA funzioni, di solito vogliamo che ciascuna delle caratteristiche \textstyle x_1, x_2, \ldots, x_n abbia un intervallo di valori simile agli altri (e abbia una media vicina allo zero). Se hai già usato PCA su altre applicazioni, potresti quindi aver pre-elaborato separatamente ogni caratteristica per avere zero media e varianza unitaria, stimando separatamente la media e la varianza di ogni caratteristica \ textstyle x_j. Tuttavia, questa non è la pre-elaborazione che applicheremo alla maggior parte dei tipi di immagini. Nello specifico, supponiamo che stiamo allenando il nostro algoritmo su “‘immagini naturali”‘, in modo che \textstyle x_j sia il valore di pixel \textstyle j. Per” immagini naturali”, intendiamo informalmente il tipo di immagine che un tipico animale o persona potrebbe vedere durante la loro vita.
Nota: Di solito usiamo immagini di scene all’aperto con erba, alberi, ecc., e ritaglia piccole (diciamo 16×16) patch di immagine casualmente da queste per addestrare l’algoritmo. Ma in pratica la maggior parte degli algoritmi di apprendimento delle funzionalità sono estremamente robusti per il tipo esatto di immagine su cui è addestrato, quindi la maggior parte delle immagini scattate con una normale fotocamera, purché non siano eccessivamente sfocate o abbiano strani artefatti, dovrebbe funzionare.
Quando ci si allena su immagini naturali, non ha molto senso stimare una media e una varianza separate per ciascun pixel, perché le statistiche in una parte dell’immagine dovrebbero (teoricamente) essere le stesse di qualsiasi altra.
Questa proprietà delle immagini si chiama “‘stazionarietà.”‘
In dettaglio, affinché PCA funzioni bene, informalmente richiediamo che (i) Le caratteristiche abbiano una media di circa zero e (ii) Le diverse caratteristiche abbiano varianze simili tra loro. Con le immagini naturali, (ii) è già soddisfatto anche senza normalizzazione della varianza, e quindi non eseguiremo alcuna normalizzazione della varianza.
(Se ti alleni su dati audio—ad esempio, su spettrogrammi—o su dati di testo—ad esempio, vettori bag-of-word—di solito non eseguiremo nemmeno la normalizzazione della varianza.)
Infatti, PCA è invariante al ridimensionamento dei dati e restituirà gli stessi autovettori indipendentemente dal ridimensionamento dell’input. Più formalmente, se si moltiplica ogni caratteristica vector \ textstyle x per un numero positivo (quindi ridimensionando ogni caratteristica in ogni esempio di allenamento con lo stesso numero), gli autovettori di output di PCA non cambieranno.
Quindi, non useremo la normalizzazione della varianza. L’unica normalizzazione che dobbiamo eseguire è la normalizzazione media, per garantire che le funzionalità abbiano una media intorno allo zero. A seconda dell’applicazione, molto spesso non siamo interessati a quanto sia luminosa l’immagine di input complessiva. Ad esempio, nelle attività di riconoscimento oggetti, la luminosità complessiva dell’immagine non influisce sugli oggetti presenti nell’immagine. Più formalmente, non siamo interessati al valore di intensità media di una patch di immagine; quindi, possiamo sottrarre questo valore, come forma di normalizzazione media.
in Concreto, se \textstyle x^{(i)} \in \Re^{n} sono i (scala di grigi) i valori di intensità di un’immagine 16×16 patch (\textstyle n=256), si potrebbe normalizzare l’intensità di ogni immagine \textstyle x^{(i)} come segue:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}
per tutti \textstyle j
Si noti che i due passaggi precedenti vengono eseguiti separatamente per ogni immagine \textstyle x^{(i)}, e che \textstyle \mu^{(i)} qui è l’intensità media dell’immagine \textstyle x^{(i)}. In particolare, questa non è la stessa cosa della stima di un valore medio separatamente per ogni pixel \ textstyle x_j.
Se stai allenando il tuo algoritmo su immagini diverse dalle immagini naturali (ad esempio, immagini di caratteri scritti a mano o immagini di singoli oggetti isolati centrati su uno sfondo bianco), altri tipi di normalizzazione potrebbero essere considerati e la scelta migliore potrebbe essere dipendente dall’applicazione. Ma quando ci si allena su immagini naturali, utilizzare il metodo di normalizzazione media per immagine come indicato nelle equazioni sopra sarebbe un valore predefinito ragionevole.
Sbiancamento
Abbiamo utilizzato PCA per ridurre la dimensione dei dati. C’è una fase di pre-elaborazione strettamente correlata chiamata sbiancamento (o, in alcune altre letterature, sphering) che è necessaria per alcuni algoritmi. Se ci stiamo allenando sulle immagini, l’input raw è ridondante, poiché i valori dei pixel adiacenti sono altamente correlati. L’obiettivo dello sbiancamento è rendere l’input meno ridondante; più formalmente, i nostri desideri sono che i nostri algoritmi di apprendimento vedano un input di allenamento in cui (i) le caratteristiche sono meno correlate tra loro e (ii) le caratteristiche hanno tutte la stessa varianza.
Esempio 2D
Per prima cosa descriveremo lo sbiancamento usando il nostro precedente esempio 2D. Descriveremo quindi come questo può essere combinato con lo smoothing e infine come combinarlo con PCA.
Come possiamo rendere le nostre funzionalità di input non correlate tra loro? Lo avevamo già fatto quando calcolavamo \ textstyle x_ {\rm rot}^{(i)} = U^Tx^{(i)}.
Ripetere la nostra figura precedente, il nostro piano per \textstyle x_{\rm rot} è:

La matrice di covarianza dei dati è data da:
\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\ end{align}
(Nota: Tecnicamente, molte delle affermazioni in questa sezione sulla “covarianza” saranno vere solo se i dati hanno zero media. Nel resto di questa sezione, prenderemo questa ipotesi come implicita nelle nostre dichiarazioni. Tuttavia, anche se la media dei dati non è esattamente zero, le intuizioni che stiamo presentando qui sono ancora vere, e quindi questo non è qualcosa di cui dovresti preoccuparti.)
Non è un caso che i valori diagonali siano \textstyle \lambda_1 e \textstyle \lambda_2. Inoltre, le voci fuori diagonale sono zero; pertanto, \ textstyle x_ {\rm rot, 1} e \ textstyle x_ {\rm rot,2} non sono correlati, soddisfacendo uno dei nostri desideri per i dati sbiancati (che le caratteristiche siano meno correlate).
Per rendere ciascuna delle nostre funzionalità di input con varianza unitaria, possiamo semplicemente ridimensionare ogni caratteristica \textstyle x_{\rm rot,i} da \textstyle 1/\sqrt{\lambda_i}. In concreto, definiamo i nostri dati sbiancati \ textstyle x_ {\rm PCAwhite} \ in \ Re^n come segue:
\begin{align}x_ {\rm PCAwhite,i} = \frac{x_ {\rm rot,i}} {\sqrt {\lambda_i}}. \ end {align}
Plotting \ textstyle x_ {\rm PCAwhite}, otteniamo:

Questo dato ha ora covarianza uguale alla matrice identity \textstyle I. Diciamo che \textstyle x_{\rm PCAwhite} è la nostra versione PCA sbiancata dei dati: I diversi componenti di \textstyle x_{\rm PCAwhite} non sono correlati e hanno varianza unitaria.
Sbiancamento combinato con riduzione della dimensionalità. Se si desidera avere dati che sono sbiancati e che sono dimensionali inferiori rispetto all’input originale, è anche possibile mantenere opzionalmente solo i componenti \textstyle k superiori di \textstyle x_{\rm PCAwhite}. Quando combiniamo lo sbiancamento PCA con la regolarizzazione (descritto più avanti), gli ultimi componenti di \textstyle x_{\rm PCAwhite} saranno quasi zero in ogni caso, e quindi possono essere tranquillamente eliminati.
ZCA Whitening
Infine, si scopre che questo modo di ottenere i dati per avere covarianza identity \textstyle I non è unico. Concretamente, se \ textstyle R è una matrice ortogonale, in modo che soddisfi \textstyle RR^T = R^TR = I (meno formalmente, se \textstyle R è una matrice di rotazione/riflessione), allora \textstyle R \,x_{\rm PCAwhite} avrà anche covarianza di identità.
In ZCA sbiancamento, scegliamo \textstyle R = U. definiamo
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
Tramando \textstyle x_{\rm ZCAwhite}, otteniamo:

Si può dimostrare che tutte le scelte possibili per \textstyle R, questa scelta di rotazione provoca \textstyle x_{\rm ZCAwhite} per essere il più vicino possibile all’originale, i dati di input \textstyle x.
Quando si utilizza ZCA sbiancamento (a differenza di PCA sbiancamento), manteniamo tutti \textstyle n dimensioni dei dati, e non provare a ridurre la sua dimensione.
Regolarizzazione
Quando si implementa PCA whitening o ZCA whitening in pratica, a volte alcuni autovalori \textstyle \lambda_i saranno numericamente vicini a 0, e quindi la fase di ridimensionamento in cui dividiamo per \sqrt{\lambda_i} comporterebbe la divisione per un valore vicino a zero; ciò potrebbe causare l’esplosione dei dati (assumere valori elevati) o altrimenti essere numericamente instabile. In pratica, implementiamo quindi questa fase di ridimensionamento utilizzando una piccola quantità di regolarizzazione e aggiungiamo una piccola costante \ textstyle \ epsilon agli autovalori prima di prendere la loro radice quadrata e inversa:il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione.\ end {align}
Quando \textstyle x prende valori intorno a \textstyle , un valore di \textstyle \epsilon \circa 10^{-5} potrebbe essere tipico.
Nel caso delle immagini, l’aggiunta di \textstyle \epsilon qui ha anche l’effetto di lisciare leggermente (o filtrare passa-basso) l’immagine di input. Ciò ha anche un effetto desiderabile di rimuovere gli artefatti di aliasing causati dal modo in cui i pixel sono disposti in un’immagine e può migliorare le funzionalità apprese (i dettagli vanno oltre lo scopo di queste note).
Lo sbiancamento ZCA è una forma di pre-elaborazione dei dati che lo mappa da \textstyle x a \textstyle x_{\rm ZCAwhite}. Si scopre che questo è anche un modello approssimativo di come l’occhio biologico (la retina) elabora le immagini. Nello specifico, man mano che l’occhio percepisce le immagini, la maggior parte dei “pixel” adiacenti nell’occhio percepirà valori molto simili, poiché le parti adiacenti di un’immagine tendono ad essere altamente correlate in intensità. È quindi uno spreco per il tuo occhio dover trasmettere ogni pixel separatamente (tramite il tuo nervo ottico) al tuo cervello. Invece, la retina esegue un’operazione di decorrelazione (questo viene fatto tramite i neuroni della retina che calcolano una funzione chiamata “on center, off surround/off center, on surround”) che è simile a quella eseguita da ZCA. Ciò si traduce in una rappresentazione meno ridondante dell’immagine di input, che viene poi trasmessa al cervello.
Implementazione di PCA Whitening
In questa sezione, riassumiamo gli algoritmi di PCA, PCA whitening e ZCA whitening e descriviamo anche come è possibile implementarli utilizzando efficienti librerie di algebra lineare.
In primo luogo, dobbiamo assicurarci che i dati abbiano (approssimativamente) media zero. Per le immagini naturali, otteniamo questo (approssimativamente) sottraendo il valore medio di ogni patch di immagine.
Otteniamo questo risultato calcolando la media per ogni patch e sottraendola per ogni patch. In Matlab, possiamo farlo usando
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);Successivamente, dobbiamo calcolare \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. Se lo stai implementando in Matlab (o anche se lo stai implementando in C++, Java, ecc., ma avere accesso a una libreria di algebra lineare efficiente), farlo come una somma esplicita è inefficiente. Invece, possiamo calcolarlo in un colpo solo come
sigma = x * x' / size(x, 2);(Controlla tu stesso la matematica per la correttezza.) Qui, assumiamo che x sia una struttura dati che contiene un esempio di allenamento per colonna(quindi, x è una matrice\textstyle n-by- \ textstyle m).
Successivamente, PCA calcola gli autovettori di \Sigma. Si potrebbe farlo usando la funzione eig Matlab. Tuttavia, poiché \ Sigma è una matrice semi-definita positiva simmetrica, è più numericamente affidabile farlo usando la funzione svd. Concretamente, se implementi
= svd(sigma);allora la matrice U conterrà gli autovettori di \Sigma (un autovettore per colonna, ordinato in ordine dall’alto verso il basso), e le voci diagonali della matrice S conterranno gli autovalori corrispondenti (ordinati anche in ordine decrescente). La matrice V sarà uguale a U e può essere tranquillamente ignorata.
(Nota: La funzione svd calcola effettivamente i vettori singolari e i valori singolari di una matrice, che per il caso speciale di una matrice semi-definita simmetrica positiva—che è tutto ciò di cui ci occupiamo qui—è uguale ai suoi autovettori e autovalori. Una discussione completa di vettori singolari rispetto agli autovettori va oltre lo scopo di queste note.)
Infine, è possibile calcolare \textstyle x_{\rm rot} e \textstyle \tilde{x} come segue:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepQuesto fornisce la rappresentazione PCA dei dati in termini di \textstyle \tilde{x} \in \Re^k. Per inciso, se x è una matrice \ textstyle n-by – \ textstyle m contenente tutti i dati di allenamento, questa è un’implementazione vettorizzata e le espressioni sopra funzionano anche per calcolare x_{\rm rot} e \tilde{x} per l’intero set di allenamento tutto in una volta. Le x_{\rm rot} e \tilde{x} risultanti avranno una colonna corrispondente a ciascun esempio di allenamento.
Per calcolare il PCA sbiancato dati \textstyle x_{\rm PCAwhite}, usare
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Dal momento che S diagonale contiene gli autovalori \textstyle \lambda_i, questo si rivelasse essere un modo compatto di calcolo \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}} contemporaneamente per tutti \textstyle i.
Infine, è anche possibile calcolare la ZCA sbiancato dati \textstyle x_{\rm ZCAwhite} come:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;