ソーベル演算子の魔法

最後に、あなたがすべて待っていた瞬間、私たちの教師なしベイズ推論シリーズの次：私たちの（そうではない）

本当に魔法のエッジ検出アルゴリズムは、それは本質的に画像内のノイズを低減し、低レベルの特徴抽出と次元低減を可能にします。 それは顔の認識の適用に特に有用でした。

アーウィン*ソーベルとゲイリー*フェルドマン（スタンフォード人工知能研究所）の1968年の愛の子供は、このアルゴリズムは、多くの現代のエッジ検出技術のイン 与えられた画像の上に二つの対向するカーネルまたはマスクを畳み込むことによって（例えば （それぞれ水平または垂直のエッジのいずれかを検出することができる）、我々はノイズの少ない、平滑化された表現を作成することができます（下-右を参照）。

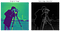
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel 各ピクセル（アンカーピクセル）とその周囲のピクセル（本質的に画像の導関数に近似する）との差を微分することによって、値（通常は輝度）。

これにより、元の画像が平滑化され、低次元の出力が生成され、低レベルの幾何学的特徴がより明確に見えるようになります。 これらの出力は、より複雑な分類アルゴリズムへの入力として、またはKullback-Leibler Divergence（KLD）を介した教師なし確率クラスタリングの例として使用できます（LBPの私の最近のブログに見られるように）。

低次元の出力を生成するには、画像の導関数を取得する必要があります。 まず、x方向とy方向の両方で導関数を計算します。 対応する軸の中心に沿ってゼロを持ち、中心のゼロに垂直な中心の正方形に2つ、各コーナーに1つを持つ2つの3×3カーネル（行列を参照）を作成します。 ゼロ以外の値のそれぞれは、ゼロの上/右（軸に依存）で正であり、対応する側で負でなければなりません。 これらのカーネルはGxとGyという名前です。

これらは次の形式で表示されます:

これらのカーネルは、画像内の各ピクセルの上に各カーネルの中心ピクセルを配置し、画像上に畳み込みます。 行列乗算を使用して、各カーネルについて、出力画像内の新しい対応するピクセルの強度値を計算します。 したがって、2つの出力画像（デカルト方向ごとに1つ）になります。目的は、画像内のピクセルと勾配行列（カーネル）内のすべてのピクセル（GxとGy）との差/変化を見つけることです。

目的は、画像内のピクセルと勾配行列（kernel）（GxとGy）の差/変化を見つけることです。

目的は、 より数学的には、これは次のように表すことができます。私たちは技術的には何も畳み込みません。

サイドノート：

私たちは技術的には何も畳み込みません。

AIや機械学習のサークルでは「畳み込み」を参照したいのですが、畳み込みには元の画像を反転させる必要があります。 数学的に言えば、畳み込みを参照するとき、入力の各3×3領域と各ピクセルのマスクとの間の相互相関を実際に計算しています。 出力イメージは、マスクと入力の間の全体的な共分散です。 これがエッジの検出方法です。

Sobelの説明に戻る…

入力のマスクと3×3セクションの間の各行列乗算の計算値が合計され、出力イメージのピクセルの最終値が生成されます。 これにより、元の画像に存在する垂直および水平のエッジの存在に関する情報を含む新しい画像が生成されます。 これは、元の画像の幾何学的特徴表現です。 さらに、この演算子は毎回同じ出力を生成することが保証されているため、この技術は画像分割タスクの安定したエッジ検出を可能にする。

これらの出力から、任意のピクセル（x、y）で勾配の大きさと勾配方向の両方を計算することができます。

大きさの大きいピクセルは画像のエッジになる可能性が高くなりますが、方向はエッジの向きについて通知します（出力を生成するための方向は必

シンプルな実装:ここでは、pythonのSobel演算子（NumPyを使用）の簡単な実装を使用して、プロセスの感触を得ています（そこにいるすべての新進コーダーのために）。

この実装は、このアルゴリズムをどのように実装するかを示すことを目的としたwikipedia pseudocode例のpythonバリアントであり、プロセスのさまざまなステップも示しています。なぜ私たちは気にするのですか？

なぜ私たちは気にしますか？

この演算子によって生成される勾配近似は比較的粗雑ですが、画像のエッジ、コーナー、およびその他の幾何学的特徴を計算する非常に計算効率 次に、ローカルバイナリパターン（この手法の詳細については、私の他のブログを参照してください）など、多くの次元削減と特徴抽出技術の道を開いています。

排他的に幾何学的特徴に依存することは、データのエンコード中に重要な情報を失う危険性がありますが、トレードオフは、データの高速前処理と高速 したがって、この手法は、入力を定義する際にテクスチャと幾何学的特徴が非常に重要であると考えることができるシナリオで特に有用です。 これが、Sobel演算子を使用して、比較的高い精度で顔認識を完了できる理由です。 ただし、色を主な差別化要因として使用する入力を分類またはグループ化しようとする場合、この手法は最良の選択ではない可能性があります。

この方法は、他の分類器を使用する前に、またはベイズ推論方法論で使用するために、幾何学的特徴の低次元表現を得るために非常に効果的であり、次元性およびノイズ低減のための優れた出発点である。