
人工ニューラルネットワーク(Ann)は、多くの相互接続されたニューロンで構成されています。
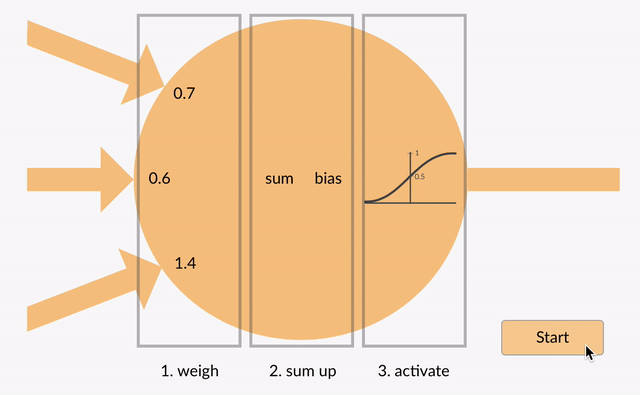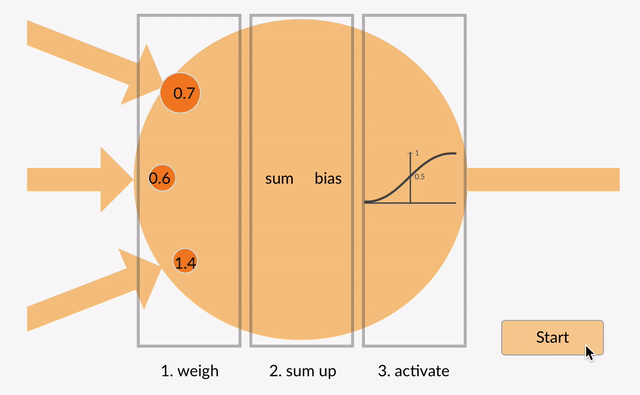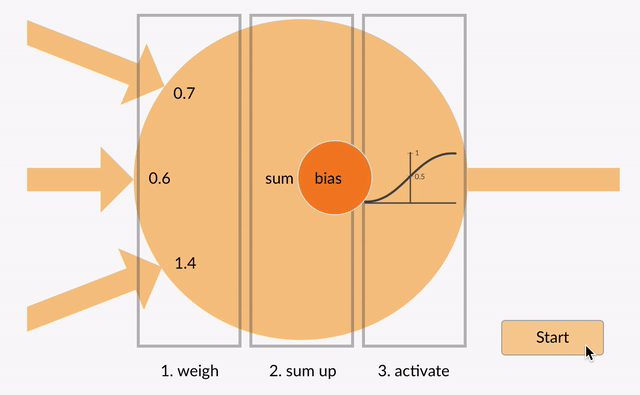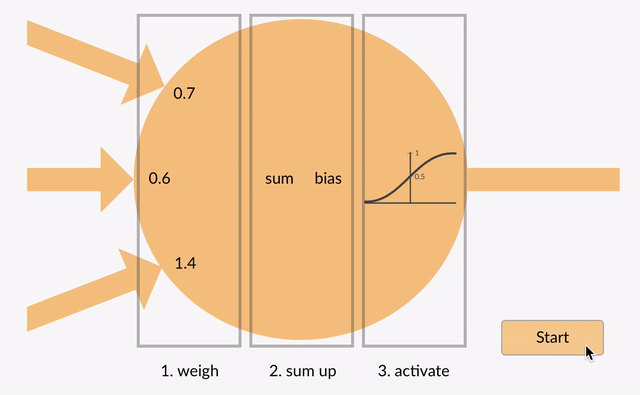
各ニューロンはいくつかの浮動小数点を取ります数字(例:1.0、0.5、-1。0)と重みとして知られているいくつかの他の浮動小数点数(例えば、0.7、0.6、1.4)でそれらを乗算します(1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). 重みは、特定の入力に焦点を当てる、または無視するメカニズムとして機能します。

加重された入力は、一緒に合計されます(例:0.7 + 0.3 + -1.4 =-04)バイアス値と一緒に(例えば-0.4+-0.1=-0.5)。合計された値(x)は、ニューロンの活性化関数(y=f(x))に従って出力値(y)に変換されます。
合計された値(x)は、ニューロンの活性化関数(y=f(x))に従って出力値(y) いくつかの一般的な活性化関数を以下に示します。

例えば-0.5→-0.05線形単位(漏れrelu)活性化関数:y=f(x)=f(-0.5)=max(0.1*-0.5、-0.5)=max(-0.05、-0.5)=-0。05
ニューロンの出力値(例えば-0.05)は、多くの場合、別のニューロンの入力です。

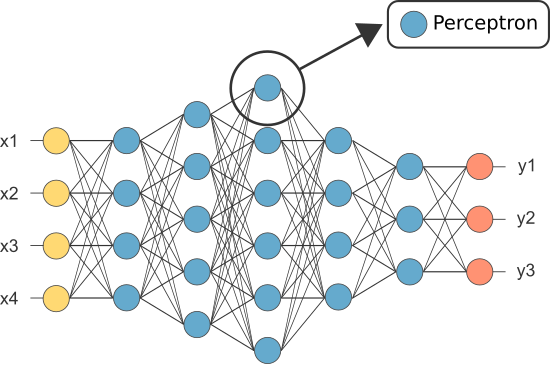
しかし、最初のannの一つはパーセプトロンとして知られており、単一のニューロンで構成されていました。

パーセプトロンの(唯一の)ニューロンの出力は、最終的な予測として機能します。

私たち自身のパーセプトロンをコード化しましょう:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(注:上記の例では学習アルゴリズムは含まれていません—別のチュートリアルで学習アルゴリズムをカバーします)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

では、ANNに非常に多くのニューロンが必要なのはなぜですか(分類子として)十分なものがあれば?

残念ながら、個々のニューロンは線形分離可能なデータを分類することしかできません。

しかし、ニューロンを組み合わせることによって、我々は本質的に彼らの決定境界を結 したがって、多くのニューロンで構成されるANNは、複雑な非線形決定境界を学習することができます。

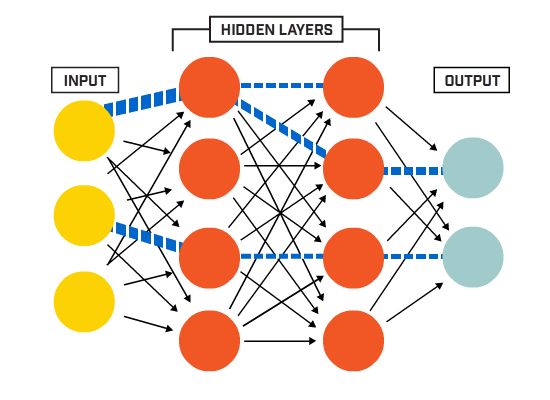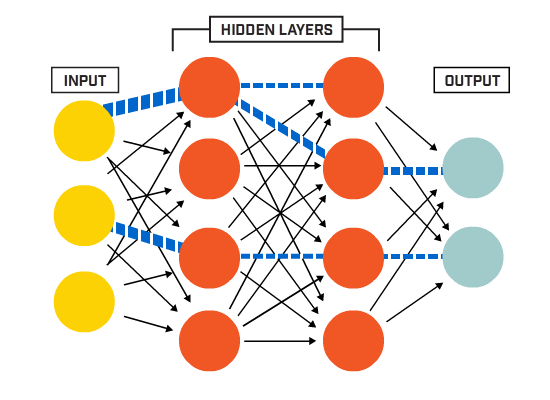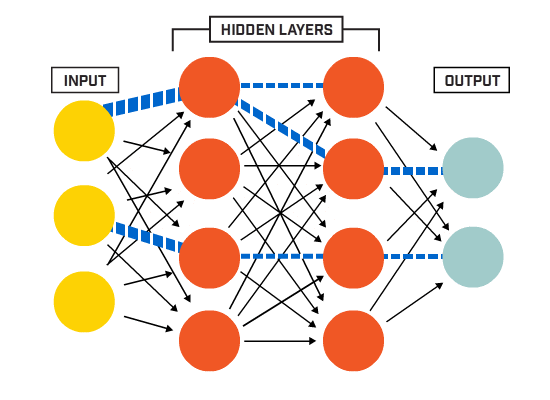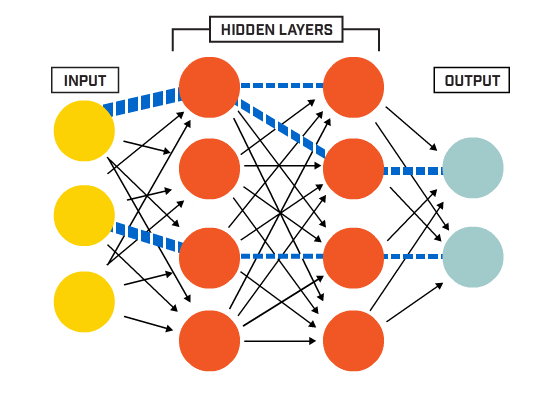
ニューロンは、特定のネットワークアーキテクチャに従って一緒に接続されています。 アーキテクチャは異なりますが、ほぼすべてのアーキテクチャにレイヤーが含まれています。 (NB: 同じ層のニューロンは互いに接続しません)
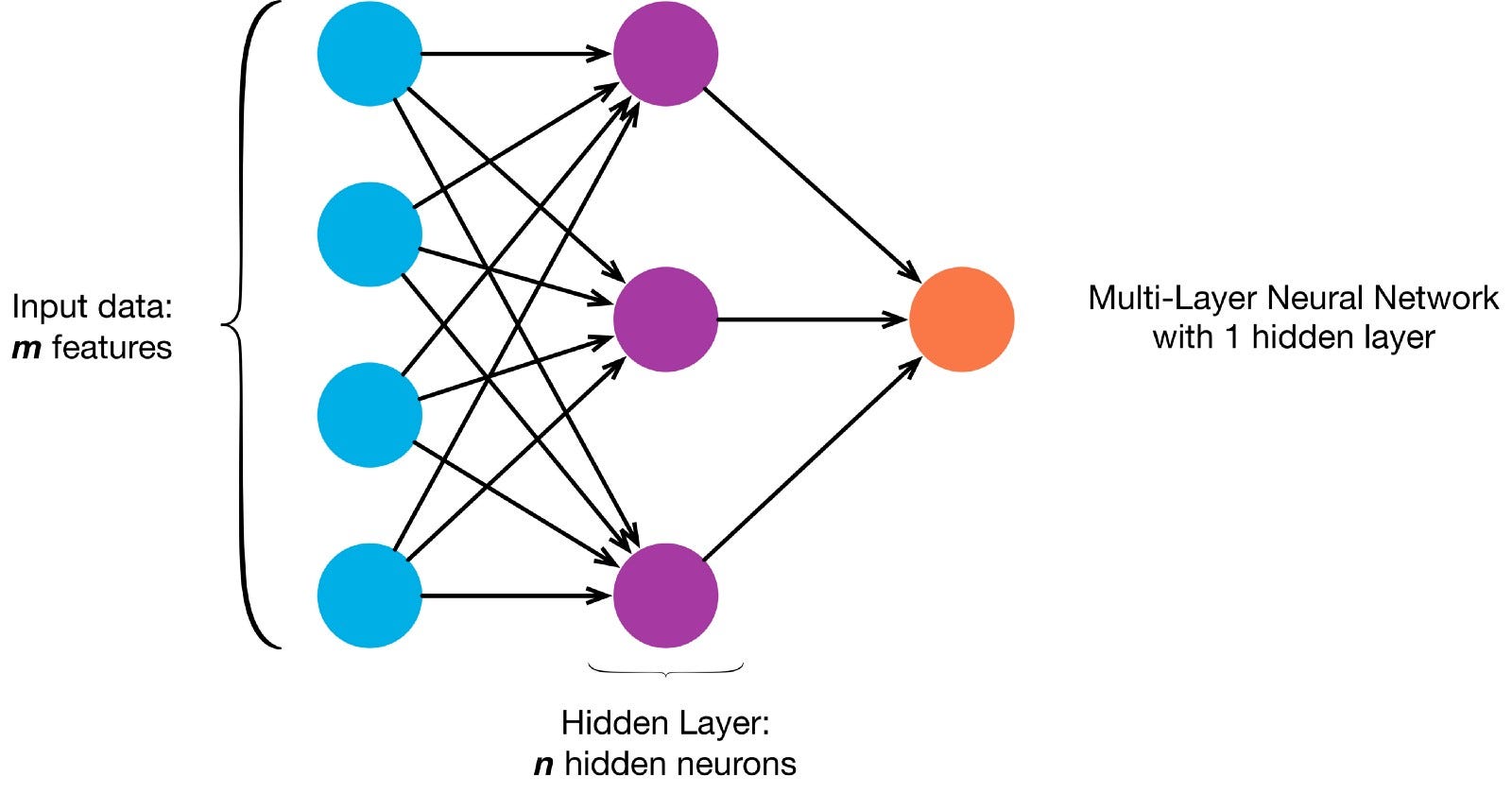
通常、入力層があります(データ)、出力層(クラスの数に等しい数のニューロンを含む)、および非表示層(任意の数のニューロンを含む)。

ニューラルネットがより複雑な決定境界を学ぶことを可能にするために、複数の隠された層が存在することができます(複数の隠された層を持つ任意のニューラルネットは、より複雑な決定境界を学ぶことができます。深いニューラルネットと考えられている)。
この絵を描くために深いNNを構築することができます:

画像をダウンarray
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
今、私たちのannにペイントを教えることは教師あり学習タスクなので、ラベル付きのトレーニングセットを作成する必要があります( 学習入力には2つの値(各ピクセルのx、y座標)があります。
画像の単純さを考えると、実際には二つの方法のいずれかでこの問題にアプローチすることができます。 分類問題(ニューラルネットは、ピクセルがxy座標を指定して”blue”クラスまたは”grey”クラスに属しているかどうかを予測する)または回帰問題(ニューラルネットは、座標を指定したピクセルのRGB値を予測する)。これを回帰問題として扱う場合:学習出力には3つの値(各ピクセルの正規化されたr、g、b値)があります。 -今のところ、この方法を使用してみましょう。
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
今、私たちのANNを作成することができます:

- 入力層には2つのニューロンが必要です(2つの値があるため、x&y座標)。
- 出力層には3つのニューロンが必要です(学習する値は3つあります:r、g、b)。
- 隠された層の数と各隠された層のニューロンの数は、実験する二つのハイパーパラメータです(だけでなく、我々はそれを訓練するエポックの数、活性化関数など)—私は10個の隠された層と100個のニューロンを使用します(これは深いニューラルネットワークになります)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
訓練されたネットワークは今、任意の座標の正規化されたrgb値を予測することができます(これは深いニューラルネットワークになります)。例えば、x、y=1,1)。
ann.predict(])
array(])
ANNを使用してすべての座標のrgb値を予測し、画像全体の予測rgb値を表示して、それがどれだけうまくいったかを確認できます(質div>
より良い結果を得るためにハイパーパラメータを変更してみてください。
これを回帰問題として扱うのではなく、これを分類問題として扱う場合、トレーニング出力には2つの値(”blue”と”grey”の2つのクラスに属するピクセルの確率)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
入力層に2つのニューロン、出力層に2つのニューロン、隠し層に100つのニューロン(隠し層に10つのニューロン)を持つバイナリ分類子としてANNを再構築することができます
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
訓練されたannを使用して、各ピクセルが属するクラス(0:”grey”または1:”blue”)を予測できるようになりました。 The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

