はじめに
主成分分析(PCA)は、教師なし特徴学習アルゴリズムを大幅に高速化するため さらに重要なのは、PCAを理解することで、多くのアルゴリズムの重要な前処理ステップであるホワイトニングを後で実装することができます。
画像のアルゴリズムを訓練しているとします。 画像内の隣接するピクセルの値は高度に相関しているため、入力はやや冗長になります。 具体的には、16×16グレースケールイメージパッチについてトレーニングしているとします。 そして、\Textstyle x\In\Re^{256}は256次元のベクトルであり、1つの特徴\textstyle x_jは各ピクセルの強度に対応します。 隣接するピクセル間の相関のために、PCAは、誤差はほとんど生じないが、はるかに低い次元の入力で入力を近似することを可能にする。私たちの実行中の例では、データセット\textstyle\{x^{(1)}、x^{(2)}、\ldots、x^{(m)}\}を\textstyle n=2次元の入力で使用し、\textstyle x^{(i)}\In\Re^2になります。 データを2次元から1に減らしたいとします。 (実際には、データを256次元から50次元に減らしたい場合がありますが、この例では低次元データを使用すると、アルゴリズムをよりよく視覚化できます。 このデータは、特徴\textstyle x_1と\textstyle x_2のそれぞれがほぼ同じ平均(ゼロ)と分散を持つように、すでに前処理されています。
説明のために、\textstyle x_1の値に応じて、各ポイントに3つの色のいずれかを着色しました。
; これらの色はアルゴリズムでは使用されず、説明のためだけのものです。PCAは、データを投影するための低次元部分空間を見つけます。
PCAは、データを投影するための低次元部分空間を見つけます。
視覚的にデータを調べることから、\textstyle u_1はデータの変動の主な方向であり、\textstyle u_2は変動の二次方向であるように見えます。
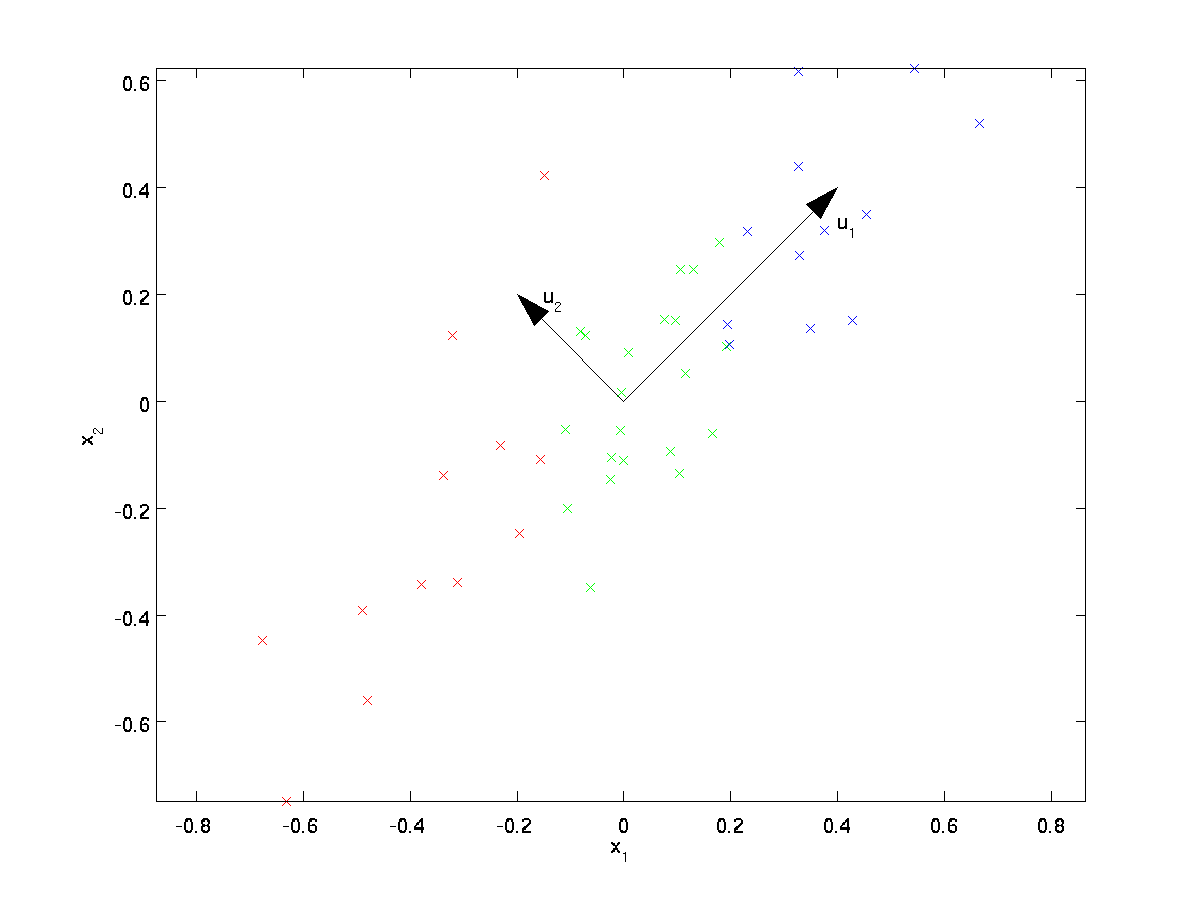
すなわち、データは\textstyle u_2よりも\textstyle u_1方向にはるかに変化する。 より形式的に方向\textstyle u_1と\textstyle u_2を見つけるには、まず行列\textstyle\Sigmaを次のように計算します:\Begin{align}\Sigma=\frac{1}{m}\sum_{i=1}^m(x^{(i)})(x^{(i)})T t。\end{align}
\textstyle xの平均がゼロの場合、\textstyle\Sigmaは正確に\textstyle xの共分散行列です。(記号”\textstyle\Sigma”は、”Sigma”と発音され、共分散行列を表すための標準記 残念ながら、\sum_{i=1}.n i;のように合計記号のように見えますが、これらは2つの異なるものです。次に、データの変動の主方向である\textstyle u_1が\textstyle\Sigmaの上(主)固有ベクトルであり、\textstyle u_2が第2固有ベクトルであることを示すことができます。\Textstyle U_1が\Textstyle\Sigmaの上(主)固有ベク注:この結果のより正式な数学的導出/正当化を見ることに興味がある場合は、PCAのCS229(機械学習)講義ノート(このページの下部にあるリンク)を参照してくださ しかし、このコースに沿って従うためにそうする必要はありません。
標準の数値線形代数ソフトウェアを使用して、これらの固有ベクトルを見つけることができます(実装ノートを参照)。 具体的には、\textstyle\Sigmaの固有ベクトルを計算し、列に固有ベクトルを積み重ねて行列\textstyle Uを形成しましょう:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.この例のベクトル\textstyle u_1と\textstyle u_2は、データを表すことができる新しい基底を形成します。 具体的には、\textstyle x\In\Re^2をいくつかのトレーニング例とします。 次に、\textstyle u_1^Txは、\textstyle xのベクトル\textstyle u_1への投影の長さ(大きさ)です。同様に、\textstyle u_2^Txはベクトル\textstyle u_2に投影された\textstyle xの大きさです。したがって、計算することにより、\textstyle(u_1、u_2)-basisで\textstyle xを表すことができます
\begin{align}x_{\rm rot}=U^Tx=\begin{bmatrix}u_1^Tx\u_2^Tx\end{bmatrix}\end{align}
(添字”rot”は、元のデータの回転(おそらく反射)に対応するという観測から来ています。 この変換されたデータ\textstyle x_{\rm rot}をプロットすると、次のようになります。\textstyle x_{\rm rot}^{(i)}=U^Tx^{(i)}すべての\textstyle iに対して、トレーニングセット全体を取り、\textstyle x_{\rm rot}^{(i)}=U^Tx^{(i)}:これは、\textstyle u_1、\textstyle u_2基底に回転されたトレーニングセットです。 一般的なケースでは、\textstyle U^Txは、基底\textstyle u_1,\textstyle u_2,…,\textstyle u_nに回転されたトレーニングセットになります。
\textstyle Uのプロパティの1つは、それが\textstyle U^TU=UU^T=Iを満たすことを意味する”直交”行列であるということです。 したがって、回転したベクトル\textstyle x_{\rm rot}から元のデータ\textstyle xに戻る必要がある場合は、計算できます
\begin{align}x=U x_{\rm rot}、\end{align}
なぜなら、\textstyle U x_{\rm rot}=UU^T x=xです。
データ次元を減らす
データの変動の主な方向は最初の次元であることがわかります。\textstyle x_{\rm rot}=UU^T x=x。
データの変動の主な方向は、最初の次元\textstyle x_{\rm rot}=UU^T x=x。
データの変動の主な方向は、最初の次元\textstyle x_{\rm rot}=UU^T x=x。
この回転されたデータのrot,1}。 したがって、このデータを1次元に減らしたい場合は、\begin{align}\tilde{x}^{(i)}=x_{\rm rot、1}.{(i)}=u_1^Tx^{(i)}\In\Reを設定できます。より一般的には、\Textstyle x\In\Re^nであり、それを\Textstyle k次元表現\textstyle\tilde{x}\In\Re^k(ここで、k<n)に縮小したい場合、\textstyle x_{\rm rot}の最初の\textstyle kコンポーネントを取ります。PCAを説明するもう1つの方法は、\textstyle x_{\rm rot}が\textstyle n次元ベクトルであり、最初のいくつかの成分が大きくなる可能性が高いことです(例: この例では、\textstyle x_{\rm rot,1}.{(i)}=u_1^Tx^{(i)}はほとんどの例\textstyle iに対して合理的に大きな値をとり、後のコンポーネントは小さくなる可能性が高い(例えば、この例では、\textstyle x_{\rm rot,2}.{(i)}=u_2^Tx^{(i)}は小さくなる可能性が高い)。 具体的には、\textstyle\tilde{x}の定義は、最初の\textstyle kコンポーネントを除くすべてがゼロである\textstyle x_{\rm rot}の近似値を使用して到達することもできます。\textstyle\tilde{x}の定義は、\textstyle x_{\rm rot}の近似値を使用することで到達することができます。 つまり、我々は持っている:\チルダ{x}=\開始{整列}開始{bmatrix}x_{\rmの腐敗、1}\vdots\x_{\rmの腐敗、k}\0\vdots\0\端{bmatrix}\約\開始{bmatrix}x_{\rmの腐敗、1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\rmの腐敗、k+1}\vdots\x_{\私たちの例では、これは私たちに\textstyle\チルダ{x}の次のプロットを与えます(\textstyle n=2、k=1を使用):しかし、上で定義した\textstyle\tilde{x}の最終\textstyle n-k成分は常にゼロであるため、これらのゼロを保持する必要はないので、\textstyle\tilde{x}を最初の\textstyle k(非ゼロ)成分だけを持つ\textstyle
これは、\textstyle u_1、u_2、\ldots、u_nベースでデータを表現したかった理由も説明しています。\textstyle kコンポーネントを維持するコンポーネントを決定するだけで、\textstyle kコンポーネ これを行うと、「top\textstyle k PCA(またはprincipal)コンポーネントを保持している」とも言います。ここで、\textstyle\tilde{x}\In\Re^kは、元の\textstyle x\In\Re^nの低次元の「圧縮」表現です。\textstyle\tilde{x}が与えられたとき、近似\textstyle\hat{x}を\textstyle xの元の値に復元するにはどうすればよいですか? 前のセクションから、\textstyle x=U x_{\rm rot}を知っています。 さらに、\textstyle\tilde{x}は、最後の\textstyle n-kコンポーネントをゼロに設定した\textstyle x_{\rm rot}の近似値と考えることができます。 したがって、\Textstyle\tilde{x}\In\Re^kが与えられた場合、\textstyle n-kゼロでそれを埋めて、\Textstyle x_{\rm rot}\In\Re^nに近似することができます。\textstyle Uを事前に乗算して、\textstyle Xに近似します。具体的には、
\begin{align}\hat{x}=U\begin{bmatrix}\tilde{x}_1\\vdots\\tilde{x}_k\\tilde{x}_k\\tilde{x}_k\\tilde{x}_k\\tilde{x}_k\\tilde{x}_k\tilde{x}_k\tilde{x}_k\tilde{x}_k\tilde{x}_k\tilde{x}_k\tilde{x}_k\tilde{x}_k\\0\\vdots\0\端{bmatrix}=\sum_{i=1}^k u_i\チルダ{x}_i。 \end{align}
上記の最終的な等式は、先に与えられた\textstyle Uの定義から来ています。 (実用的な実装では、実際にはゼロパッド\textstyle\tilde{x}を乗算してから\textstyle Uを乗算することはありません。\Textstyle Uの最初の\textstyle k列を\Re^kに乗算するだけです。\Textstyle U上記の最後の式 これをデータセットに適用すると、\textstyle\hat{x}の次のプロットが得られます:p>
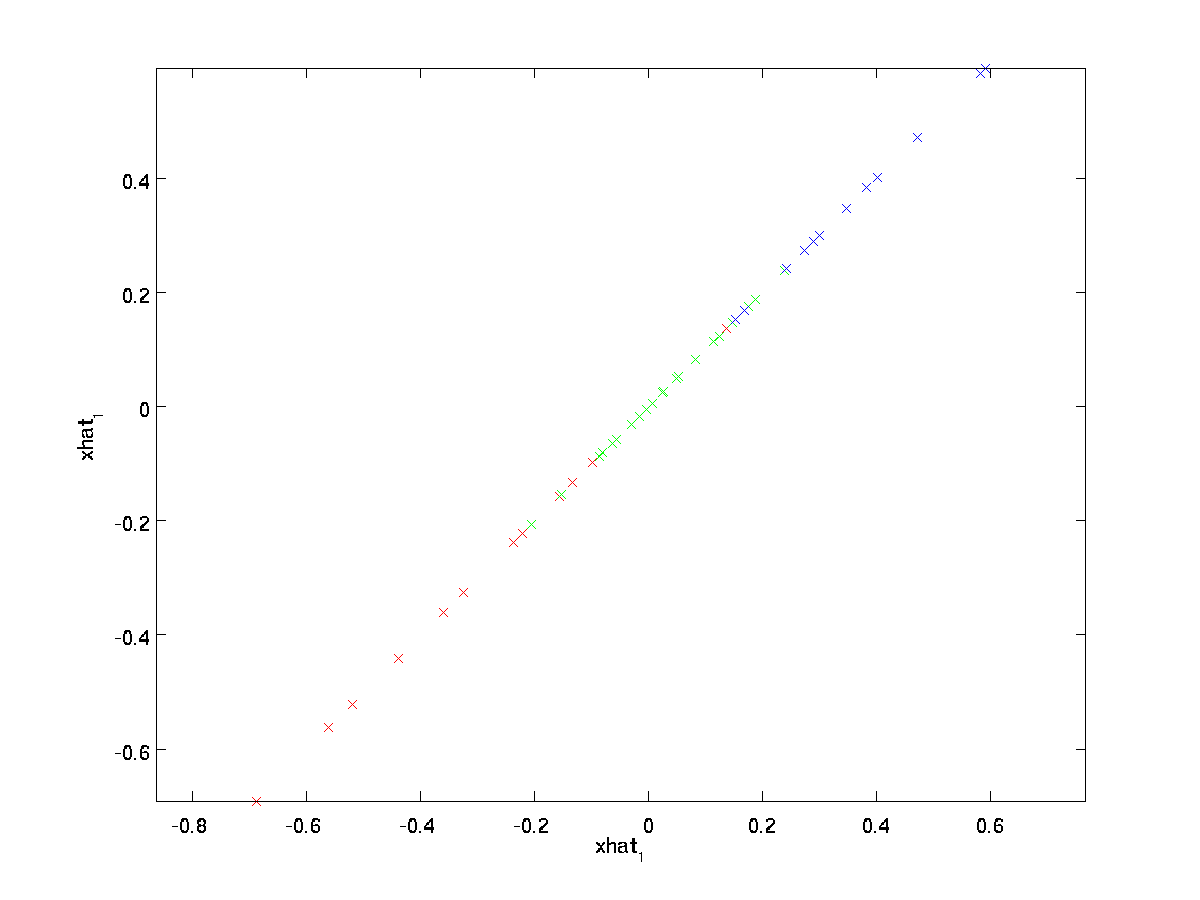
したがって、元のデータセットに1次元近似を使用しています。
オートエンコーダーや他の教師なし特徴学習アルゴリズムをトレーニングしている場合、アルゴリズムの実行時間は入力の次元によって異なります。 \Textstyle\tilde{x}\In\Re^kを\textstyle xではなく学習アルゴリズムにフィードすると、低次元入力でトレーニングされるため、アルゴリズムが大幅に高速に実行される可能性があ 多くのデータセットでは、低次元の\textstyle\tilde{x}表現は元のものに非常に良い近似であり、この方法でPCAを使用すると、近似誤差はほとんど発生しませんが、アルゴ
保持するコンポーネントの数
どのように設定しますかtextstyle k;つまり、保持する必要があるPCAコンポーネントの数は何ですか? 私たちの単純な2次元の例では、2つの成分のうち1つを保持するのは自然なようでしたが、より高い次元のデータでは、この決定はそれほど簡単では \Textstyle kが大きすぎる場合は、データをあまり圧縮することはありません。\textstyle k=nの制限では、元のデータを使用しています(ただし、別の基準に回転しています)。 逆に、\textstyle kが小さすぎる場合、データに非常に悪い近似を使用している可能性があります。具体的には、\textstyle k=nの場合、データに正確な近似値があり、分散の100%が保持されていると言います。\textstyle kを設定する方法を決定するには、通常、\textstyle kの異なる値の”‘保持された分散の割合”‘を見ていきます。\textstyle k=nの場合、データに正確な近似値があり、分散の100%が保持されていると言います。 I.e.、元のデータの変化のすべてが保持されます。 逆に、\textstyle k=0の場合、すべてのデータをゼロベクトルで近似しているため、分散の0%が保持されます。より一般的には、\textstyle\lambda_1,\lambda_2,\ldots,\lambda_nを\textstyle\Sigmaの固有値(降順にソート)とすると、\textstyle\lambda_jは固有ベクトル\textstyle u_jに対応する固有値になります。\textstyle k主成分を保持する:align\sum_{j=1}^k\lambda_j}{\sum_{j=1}^n\lambda_j}を開始します。\end{align}
上記の単純な2Dの例では、\textstyle\lambda_1=7.29、および\textstyle\lambda_2=0.69です。 したがって、\textstyle k=1主成分のみを保持することによって、\textstyleを保持しました7.29/(7.29+0.69) = 0.913, または分散の91.3%。
保持されている分散の割合のより正式な定義は、これらのノートの範囲を超えています。 しかし、\textstyle\lambda_j=\sum_{i=1}.m x_{\rm rot、j}.2であることを示すことは可能です。 したがって、\textstyle\lambda_j\approx0の場合、それは\textstyle x_{\rm rot、j}が通常は0に近いことを示しており、定数0で近似することで比較的ほとんど失われません。 これはまた、下部のものではなく、上部の主成分(\textstyle\lambda_jの大きな値に対応する)を保持する理由も説明しています。 一番上の主成分\textstyle x_{\rm rot,j}は、より変数が大きく、より大きな値を取るものであり、それらをゼロに設定するとより大きな近似誤差が発生します。\textstyle x_{\rm rot,j}画像の場合、一般的な発見的な方法の1つは、分散の99%を保持するように\textstyle kを選択することです。
画像の場合、分散の99%を保持するように\textstyle kを選 Other sum_{j=1}k k\lambda_j}{\sum_{j=1}.n\lambda_j}\geq0.99を満たす\textstyle kの最小値を選択します。 \end{align}
アプリケーションによっては、追加のエラーが発生する場合は、90-98%の範囲の値も使用されることがあります。 PCAをどのように適用したかを他の人に説明すると、分散の95%を保持するために\textstyle kを選択したと言っても、120(または他の数の)コンポーネントを保持してPCAが機能するためには、通常、各機能\textstyle x_1、x_2、\ldots、x_nが他の機能と同様の値の範囲を持つ(そして平均がゼロに近い)ことが必要です。 以前に他のアプリケーションでPCAを使用したことがある場合は、各フィーチャ\textstyle x_jの平均と分散を別々に推定することにより、各フィーチャを別々に前処理して平均と単位分散がゼロになる可能性がありますが、これはほとんどのタイプの画像に適用される前処理ではありません。 具体的には、\textstyle x_jがpixel\textstyle jの値になるように、”‘natural images”‘上でアルゴリズムをトレーニングしているとします。”natural images”とは、典型的な動物や人が生涯にわたって見るかもしれないイメージのタイプを非公式に意味します。ノート
: 通常私達は草、木、等が付いている屋外場面のイメージを使用します。 そして、アルゴリズムを訓練するために、これらからランダムに小さな(例えば16×16)画像パッチを切り しかし、実際には、ほとんどの特徴学習アルゴリズムは、訓練された画像の正確なタイプに対して非常に堅牢であるため、過度にぼやけたり、奇妙なアーティファクトを持っていない限り、通常のカメラで撮影されたほとんどの画像は機能するはずです。
自然な画像を訓練するとき、画像のある部分の統計は(理論的に)他の部分と同じでなければならないので、各ピクセルについて別々の平均と分散を推
この画像の性質は””定常性”と呼ばれています。詳細には、PCAがうまく機能するためには、非公式には、(i)特徴がほぼゼロ平均を持ち、(ii)異なる特徴が互いに類似した分散を有することが必要である。 自然な画像では、(ii)は分散正規化がなくてもすでに満たされているため、分散正規化は実行されません。
(オーディオデータ、たとえばスペクトログラム、またはテキストデータ、たとえばbag—of—wordベクトルをトレーニングしている場合、通常は分散正規化も実行しません。)
実際、PCAはデータのスケーリングに対して不変であり、入力のスケーリングに関係なく同じ固有ベクトルを返します。 より正式には、各特徴ベクトル\textstyle xに正の数を掛けた場合(したがって、すべての訓練例のすべての特徴を同じ数でスケーリングする)、PCAの出力固有ベクトルしたがって、分散正規化は使用しません。 次に実行する必要がある唯一の正規化は、特徴量がゼロの周りに平均を持つことを保証するために、平均正規化です。 アプリケーションによっては、非常に多くの場合、入力画像全体の明るさには関心がありません。 たとえば、物体認識タスクでは、画像の全体的な明るさは、画像内に存在するオブジェクトには影響しません。 より正式には、画像パッチの平均強度値には関心がないため、平均正規化の形式としてこの値を減算することができます。具体的には、\Textstyle x^{(i)}\In\Re^{n}が16×16画像パッチの(グレースケール)強度値である場合(\textstyle n=256)、各画像\textstyle x^{(i)}の強度を次のように正規化することができます。
\mu^{(i)}:=\frac{1}{n}\sum_{j=1}n n x^{(i)}_jx^{(i)}}_j : ここで、\textstyle\mu^{(i)}は画像\textstyle x^{(i)}の平均強度です。\textstyle\mu^{(i)}は画像\textstyle x^{(i)}の平均強度です。\textstyle\mu^{(i)}は画像\textstyle x^{(i)}の平均強度です。\textstyle\mu^{(i)}は画像\textstyle x^{(i)}の平均強度です。\textstyle\mu^{(i)}は画像\textstyle x^{(i)}の 特に、これは、各ピクセル\textstyle x_jごとに平均値を個別に推定することと同じではありません。
自然な画像以外の画像(手書きの文字の画像や、白い背景を中心とした単一の孤立したオブジェクトの画像など)でアルゴリズムをトレーニングする場合は、他のタイプの正規化を検討する価値があり、最良の選択はアプリケーションに依存する可能性があります。 しかし、自然な画像でトレーニングする場合、上記の式で与えられた画像ごとの平均正規化法を使用することは合理的なデフォルトです。
ホワイトニング
データの次元を減らすためにPCAを使用しました。 いくつかのアルゴリズムに必要なホワイトニング(または、いくつかの他の文献では、sphering)と呼ばれる密接に関連する前処理ステップがあります。 画像を訓練している場合、隣接するピクセル値は高度に相関しているため、生の入力は冗長です。 より正式には、私たちのdesiderataは、私たちの学習アルゴリズムは、(i)特徴が互いにあまり相関しておらず、(ii)特徴がすべて同じ分散を持っている訓練入力を見
2Dの例
まず、前の2Dの例を使用してホワイトニングについて説明します。 次に、これを平滑化とどのように組み合わせることができるか、そして最後にこれをPCAとどのように組み合わせるかについて説明します。
入力フィーチャを互いに相関しないようにするにはどうすればよいですか? 私たちはすでに\textstyle x_{\rm rot}.{(i)}=U^Tx^{(i)}を計算するときにこれを行っていました。前の図を繰り返して、\textstyle x_{\rm rot}のプロットは次のとおりです。

このデータの共分散行列は次のように与えられます。
\begin{align}\begin{bmatrix}7.29&&&&&&0.69\end{bmatrix}です。\end{align}
(注: 技術的には、このセクションの「共分散」に関する記述の多くは、データの平均がゼロの場合にのみ真実になります。 このセクションの残りの部分では、この仮定を私たちの声明の中で暗黙のものとします。 しかし、データの平均が正確にゼロではない場合でも、ここで提示している直感はまだ真実であるため、これは心配すべきことではありません。対角値が\textstyle\lambda_1および\textstyle\lambda_2であることは偶然ではありません。 さらに、非対角エントリはゼロです; したがって、\textstyle x_{\rm rot,1}と\textstyle x_{\rm rot,2}は相関がなく、白化されたデータ(特徴の相関が低い)のdesiderataの1つを満たします。各入力フィーチャに単位分散を持たせるには、各フィーチャ\textstyle x_{\rm rot,i}を\textstyle1/\sqrt{\lambda_i}で再スケールするだけです。 具体的には、白色化されたデータ\textstyle x_{\rm PCAwhite}\In\Re^nを次のように定義します。
\begin{align}x_{\rm PCAwhite、i}=\frac{x_{\rm rot、i}}{\sqrt{\lambda_i}}。 \end{align}
プロット\textstyle x_{\rm PCAwhite}、我々は得る:このデータは、単位行列\textstyle Iに等しい共分散を持ちます。\textstyle x_{\rm PCAwhite}は、データのPCAホワイト化バージョンであると言います。\textstyle x_{\rm PCAwhite}のさまざまなコンポーネントは無
次元削減と組み合わせたホワイトニング。 元の入力よりも低次元のデータを白くしたい場合は、必要に応じて\textstyle x_{\rm PCAwhite}のトップ\textstyle kコンポーネントのみを保持することもできます。 PCAの白化と正則化(後述)を組み合わせると、\textstyle x_{\rm PCAwhite}の最後のいくつかのコンポーネントはほぼゼロになるため、安全に削除できます。最後に、データを共分散id\textstyle Iを持つようにするこの方法は一意ではないことがわかりました。 具体的には、\textstyle Rが任意の直交行列であるため、\textstyle RR^T=R^TR=I(形式的ではないが、\textstyle Rが回転/反射行列である場合)を満たす場合、\textstyle R\,x_{\rm PCAwhite}も恒等共分散を持ちます。私たちは定義します
\begin{align}x_{\rm Zcawhite}=U x_{\rm PCAwhite}\end{align}
プロット\textstyle x_{\rm ZCAwhite}、私たちは得る:

それはすべての可能な選択\textstyle rの場合、この回転の選択により、\textstyle x_{\Rm Zcawhite}は元の入力データ\Textstyle Xにできるだけ近くなります。
zcaホワイトニングを使用する場合(pcaホワイトニングとは異なり)、通常、データのすべての\textstyle n次元を保持し、その次元を減らそうとしません。
Regularizaton
PCAホワイトニングまたはZCAホワイトニングを実際に実装する場合、固有値\textstyle\lambda_iの一部が数値的に0に近いため、\sqrt{\lambda_i}で除算するスケーリングステップは、ゼロに近い値で除算することを含みます。これにより、データが爆発する(大きな値を取る)か、数値的に不安定になる可能性があります。 したがって、実際には、少量の正則化を使用してこのスケーリングステップを実装し、平方根と逆数を取る前に固有値に小さな定数\textstyle\epsilonを追加します:/X_{\rm pcawhite、i}=\frac{x_{\rm rot、i}}{\sqrt{\lambda_i+\epsilon}}を開始します。\end{align}
\textstyle xが\textstyleの周りの値を取るとき、\textstyle\epsilon\approx10^{-5}の値が典型的な場合があります。画像の場合、ここに\textstyle\epsilonを追加すると、入力画像をわずかに平滑化(またはローパスフィルタリング)する効果もあります。
画像の場合、ここに\textstyle\epsilonを追加 これは、画像内のピクセルの配置方法によって引き起こされるエイリアシングアーティファクトを除去する望ましい効果もあり、学習された機能を改善することができます(詳細はこれらのノートの範囲を超えています)。ZCAホワイトニングは、\textstyle xから\textstyle x_{\rm ZCAwhite}にマップするデータの前処理の一形態です。 これは、生物学的眼(網膜)が画像をどのように処理するかの大まかなモデルでもあることが判明しました。 具体的には、あなたの目が画像を知覚するとき、あなたの目の中のほとんどの隣接する「ピクセル」は、画像の隣接する部分が強度において高度に相関 したがって、すべてのピクセルを(視神経を介して)別々に脳に送信する必要があるのは、目にとって無駄です。 代わりに、あなたの網膜はZCAによって実行されるものと同様の非相関操作(これは「on center、off surround/off center、on surround」と呼ばれる関数を計算する網膜ニューロンを介し これはあなたの頭脳に送信される入力イメージのより少なく重複した表現で起因する。
PCAホワイトニングの実装
このセクションでは、PCA、PCAホワイトニング、ZCAホワイトニングアルゴリズムを要約し、効率的な線形代数ライブラリを使用してそれらを実装する方法についても説明します。最初に、データが(およそ)ゼロ平均を持つことを確認する必要があります。
最初に、データが(およそ)ゼロ平均を持つことを確認する必要があります。 自然な画像の場合、各画像パッチの平均値を減算することによって、これを(およそ)達成します。
これは、各パッチの平均を計算し、各パッチの平均を減算することによって達成されます。 次に、\textstyle\Sigma=\frac{1}{m}\sum_{i=1}m m(x^{(i)})(x^{(i)})T Tを計算する必要があります。 しかし、効率的な線形代数ライブラリへのアクセス権を持っている)、明示的な合計としてそれを行うことは非効率的です。 代わりに、これを一気に計算することができます
sigma = x * x' / size(x, 2);(正確さのために数学を自分で確認してくださ ここで、xは列ごとに1つのトレーニング例を含むデータ構造であると仮定します(したがって、xは\textstyle n行\textstyle m列の行列です)。
次に、PCAは\Sigmaの固有ベクトルを計算します。 これは、Matlab eig関数を使用して行うことができます。 ただし、\Sigmaは対称正半定値行列であるため、関数svdを使用してこれを行う方が数値的に信頼性が高くなります。 具体的には、
= svd(sigma);を実装すると、行列Uには\Sigmaの固有ベクトル(列ごとに1つの固有ベクトル、上から下の固有ベクトルの順にソート)が含まれ、行列Sの対角エントリには対応する固有値が含まれます(降順でもソートされます)。 行列VはUと等しくなり、無視しても問題ありません。
(注: Svd関数は実際には行列の特異ベクトルと特異値を計算しますが、これは対称正半定値行列の特殊な場合(ここで関係しているのはすべて)、その固有ベ 特異ベクトルと固有ベクトルの完全な議論は、これらのノートの範囲を超えています。最後に、次のように\textstyle x_{\rm rot}と\textstyle\tilde{x}を計算できます。
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepこれは、\Re^kの\textstyle\tilde{x}\の観点からデータのPCA表現を与えます。 ちなみに、xがすべてのトレーニングデータを含む\textstyle n-by-\textstyle m行列の場合、これはベクトル化された実装であり、上記の式はx_{\rm rot}と\tilde{x}を計算するためにも 結果のx_{\rm rot}と\tilde{x}は、各トレーニング例に対応する1つの列を持ちます。Sの対角には固有値\textstyle\lambda_iが含まれているため、これは\textstyle x_{\rm PCAwhite,i}=\frac{x_{\rm rot,i}}{\sqrt{2}}}を計算するコンパクトな方法であることがわかります。最後に、zcaホワイト化されたデータ\textstyle x_{\rm zcawhite}を次のように計算することもできます。
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x; xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x; xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x; xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x; xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;