機械および深層学習の実践では、モデルパラメータは、分類器または他のMLモデルによる訓練中に自 たとえば、重みとバイアス、またはデシジョンツリーの分割ポイントなどです。
モデルのハイパーパラメータは、代わりにトレーニングプロセス全体を管理するプロパティです。 これらには、ネットワーク構造を決定する変数(たとえば、隠れた単位の数)と、ネットワークの学習方法を決定する変数(たとえば、学習率)が含まれます。 モデルのハイパーパラメータは、トレーニングの前(重みとバイアスを最適化する前)に設定されます。
たとえば、モデルに組み込まれた構成変数がいくつかあります。
- 学習率
- エポック数
- 隠しレイヤ
- 隠しユニット
- 活性化関数
ハイパーパラメータは、トレーニングアルゴの動作を直接制御し、トレーニング中のモデルのパフォーマンスに重要な影響を与えるため、重要です。
適切なハイパーパラメータを選択することは、学習されたモデルへの影響を考えると、ニューラルネットワークアーキテクチャの成功に重要な役割を果 たとえば、学習率が低すぎると、モデルはデータ内の重要なパターンを見逃し、逆に高い場合は衝突が発生する可能性があります。
優れたハイパーパラメータを選択すると、二つの主な利点があります。
- 可能なハイパーパラメータの空間にわたって効率的な検索;と
- ハイパーパラメータチューニングのための実験の大規模なセットの管理が容易になります。
ハイパーパラメータは大きく2つのカテゴリに分けることができます。
1。 オプティマイザハイパーパラメータ,
2. モデル固有のハイパーパラメータ
これらは、最適化とトレーニングプロセスに関連しています。
1.1. 学習率:
モデル学習率が最適値よりも小さすぎる場合、理想的な状態に到達するまでにははるかに長い時間(数百または数千)のエポックがかかります。
一方、学習率が最適値よりもはるかに大きい場合、それは理想的な状態をオーバーシュートし、アルゴリズムは収束しない可能性があります。 合理的な開始学習率=0.001。/div>それを考慮するには:
a)モデルは、それぞれ独自の誤差曲線を持つ数百と数千のパラメータを持っています。 そして、学習率はそれらのすべてを羊飼いする必要があります
b)誤差曲線はきれいなu字型ではありません。
1.2. ミニバッチサイズ:
バッチサイズは、トレーニングプロセスのリソース要件、速度、反復回数に影響を与えます。
歴史的に、データセットの単一の例をモデルに適合させ、一つの例だけを使用して前方パスを実行し、誤差/逆伝播を計算する確率的トレーニングを行う そして、データセット内の各例に対してこれをもう一度行います。または、データ全体をトレーニングステップに供給し、データセット内のすべての例を見て生成された誤差を使用して勾配を計算する方がよいでしょう。
これはバッチトレーニングと呼ばれます。p>
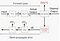
一般的に使用される技術は、今日はミニを設定することです-バッチサイズ。 確率的学習は、ミニバッチサイズ=1の場合であり、バッチ学習は、ミニバッチサイズ=トレーニングセット内の例の数の場合です。 実験のための推奨される開始値: 1, 2, 4, 8, 16, 32, 64, 128, 256.
ミニバッチサイズを大きくすると、学習計算で行列乗算を利用する計算ブーストが可能になります。 しかし、それは訓練プロセスのためのより多くの記憶を必要とすることを犠牲にして来る。 ミニバッチサイズを小さくすると、誤差計算でより多くのノイズが発生し、多くの場合、学習プロセスが局所最小値で停止するのを防ぐのに便利です。 ミニバッチサイズの公正価値=32。
だから、計算ブーストはミニバッチサイズを増やすために私たちを駆動しながら、この実用的なアルゴリズムの利点は、実際にそれを小さくするため1.3.
1.3. エポック数:
トレーニングステップのエポック数を適切に選択するには、注意する必要があるメトリックは検証エラーです。/div>直感的な手動の方法は、検証誤差が減少し続ける限り、多くの反復回数の鉄道模型を持つことです。これは、過去10または20のエポックで検証エラーが改善されていない場合に備えて、トレーニングプロセスを停止することです。
2. モデルハイパーパラメータ
彼らはモデルの構造にもっと関与しています:
2.1。 隠されたユニットの数:
隠されたユニットの数は、より神秘的なハイパーパラメータの一つです。 ニューラルネットワークは普遍的な関数近似器であり、関数(または予測タスク)を近似することを学ぶためには、関数を学ぶのに十分な”能力”が必要で 隠された単位の数は、モデルの学習能力の主な尺度です。
単純な関数の場合、隠し単位の数が少なくなる可能性があります。 関数が複雑になればなるほど、モデルが必要とする学習能力が高くなります。
ユニットの数が少し多い場合、最適な数は問題ではありませんが、はるかに大きな数は過剰適合につながります(つまり、あまりにも多くの容量を持つモデルを提供すると、過剰適合する傾向があり、データセットを”暗記”しようとするため、一般化する能力に影響を与える可能性があります)
2.2。 最初の隠された層:
最初の隠れ層を含むもう一つのヒューリスティックは、経験的観察によると、隠れユニットの数を入力の数よりも大きく設定すると、タスクの数2.3.
2.3. 層の数:
3層ニューラルネットは2層のニューラルネットよりも優れていることがよくあります。 しかし、さらに深く行くことはめったにはるかに役立ちません。 (例外は、畳み込みニューラルネットワークであり、より深いほど、より良いパフォーマンスを発揮します)。
ハイパーパラメータ最適化技術
機械学習で最も最適なハイパーパラメータを見つけるプロセスは、ハイパーパラメータ最適化と呼ばれます。
一般的なアルゴリズムは次のとおりです。
- グリッド検索
- ランダム検索
- ベイズ最適化
グリッド検索
グリッド検索は、ハイパーパラメータを実装するための伝統的な手法です。 それはややブルートフォースすべての組み合わせについてです。 グリッド検索には、ハイパーパラメータの2つのセットを作成する必要があります:
- 学習率
- 層の数
グリッド検索は、ハイパーパラメータの二つのセット(学習率と層の数)を使用して、すべての組み合わせのアルゴリズムを訓練し、交差 この検証手法は、訓練されたモデルがデータセットからほとんどのパターンを取得することを保証します(モデルを訓練するための十分なデータと検証のための十分なデータを提供するのに役立つ”K-Fold Cross Validation”を使用して検証を実行するための最良の方法の1つ)。
グリッド探索法は、使用するより簡単なアルゴリズムですが、データが次元の呪いと呼ばれる高い次元空間を持っている場合、それは苦しみます。
Random Search
検索空間をランダムにサンプリングし、指定された確率分布からセットを評価します。 たとえば、100,000個のサンプルをすべてチェックしようとする代わりに、1,000個のランダムなパラメータをチェックすることができます。しかし、ランダム探索アルゴリズムを使用することの欠点は、次のセットを選択するために以前の実験からの情報を使用しないことです。
さらに、次の実験を予測することは困難である。

ベイズ最適化
ハイパーパラメータの設定は、検証セットのモデルのパフォーマンスを最大化します。 MLアルゴは、モデルのハイパーパラメータの微調整を頻繁に必要とします。 残念なことに、その調整は、式に書き込むことができないため、しばしば「黒関数」と呼ばれます(関数の導関数は不明です)。
&ハイパーパラメータの微調整を最適化するより魅力的な方法は、ベイズ最適化を使用するなど、自動化されたモデルチューニングアプローチ 目的関数を近似するために使用されるモデルは、サロゲートモデルと呼ばれます。 ベイズ最適化のための一般的なサロゲートモデルは、ガウス過程(GP)です。 ベイズ最適化は、通常、未知の関数がガウス過程(GP)からサンプリングされたと仮定し、観測が行われるときにこの関数の事後分布を維持することに
ベイズ最適化を実行するときに行うべき二つの主要な選択肢があります。
- 最適化される関数についての仮定を表現する関数よりも前に選 このために、我々は前にガウス過程を選択します。
- 次に、我々は私たちが評価するために次の点を決定することができ、モデル事後から効用関数を構築す
ガウスプロセス
ガウスプロセスは、いくつかのデータを見た後、事後関数に変換することができる関数上の事前分布を定義します。 ガウス過程では、共分散行列を使用して、値が確実に近接していることを確認します。 共分散行列と期待値μ(x)を出力する平均μ関数は、ガウス過程を定義します。
1. ガウス過程は、ベイズ推論のための事前として使用されます。
2。 事後を計算することで、目に見えないテストケースの予測を行うために使用することができます。

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. 一般的な取得関数は、
- 改善の最大確率(MPI)
- 期待される改善(EI)
- 上部信頼限界(UCB)
期待される改善(EI)は一般的なものであり、次のように定義されます。
EI(x)=π
ここで、π(x)はハイパーパラメータの現在の最適なセットです。 ハイパーパラメータを最大化すると、σに改善されます。/div>