深い残差ネットワーク(ResNet)は、Microsoft Researchが画像認識のための深い残差学習をリリースしたときに、深い学習の世界を嵐に これらのネットワークは、画像分類、オブジェクト検出、およびセマンティックセグメンテーションをカバーしたImageNetとCOCO2015大会のすべての主要なトラックで1位の入賞作品につながった。 Resnetの堅牢性は、以来、様々な視覚認識タスクと音声と言語を含む非視覚的なタスクによって証明されています。 また、博士論文の研究では、他の深層学習モデルに加えてResNetを使用しました。
私は元の論文は、モデル/ネットワークの最も直感的で詳細な説明を与えると信じているので、この記事は、すべてのResNetの発明者Kaiming彼によって書かれたまた うまくいけば、この記事はあなたが残留ネットワークの要点をよりよく理解するのに役立つかもしれません。
- 画像認識のための深い残差学習
- 深い残差ネットワークにおけるアイデンティティマッピング
- 深いニューラルネットワークのための集約残差変換
深い残差ネットワーク上の直感(stackoverflow ref)
残差ブロックは、次のように表示されます。
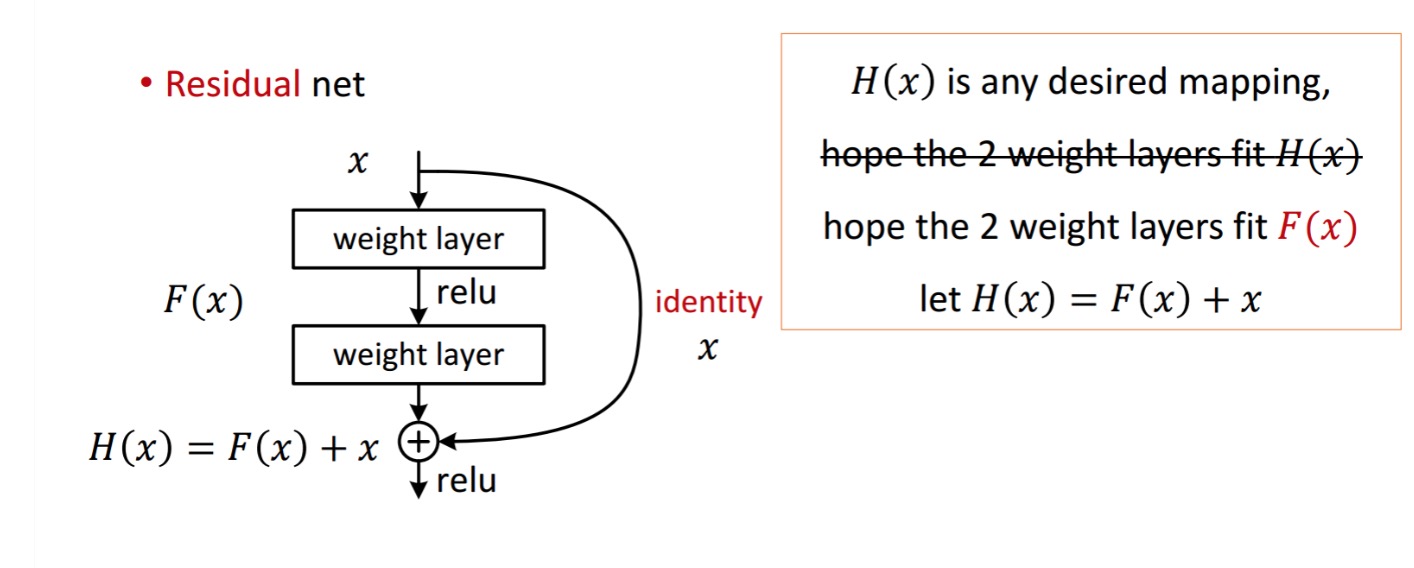
残差ブロックは、次のように表示されます。

二つの重み層で処理することによって取得します。 次に、取得するために追加します。 今、それがあなたの地上の真実と一致するあなたの理想的な予測された出力であると仮定してください。 以来、希望を得ることは完璧を得ることに依存します。 つまり、残留ユニット内の2つの重量層が実際に所望のものを生成することができ、理想を得ることが保証されることを意味する。
は、以下のようにして得られる。
は、以下のようにして得られる。
著者らは、残差マッピング(すなわち)よりも最適化が容易である可能性があると仮定している。 簡単な例で説明するために、理想と仮定します。 次に、直接マッピングの場合、次のような非線形層のスタックがあるため、恒等写像を学ぶことは困難です。
したがって、これらすべての重みとReluを中央に持つ恒等写像を近似することは困難です。
ここで、目的のマッピングを定義する場合は、次のようにgetが必要です。
上記を達成するのは簡単です。 任意の重みをゼロに設定するだけで、ゼロ出力が得られます。 戻って追加し、あなたの希望のマッピングを取得します。
画像認識のための深い残差学習
問題
より深いネットワークが収束し始めると、劣化の問題が公開されています。
動作中の劣化を見て:
私たちはそれに多くの層を追加することによって、浅いネットワークとその深い対応を取りましょう。
最悪のシナリオ:深いモデルの初期の層は浅いネットワークに置き換えることができ、残りの層はちょうど恒等関数(出力に等しい入力)として機能
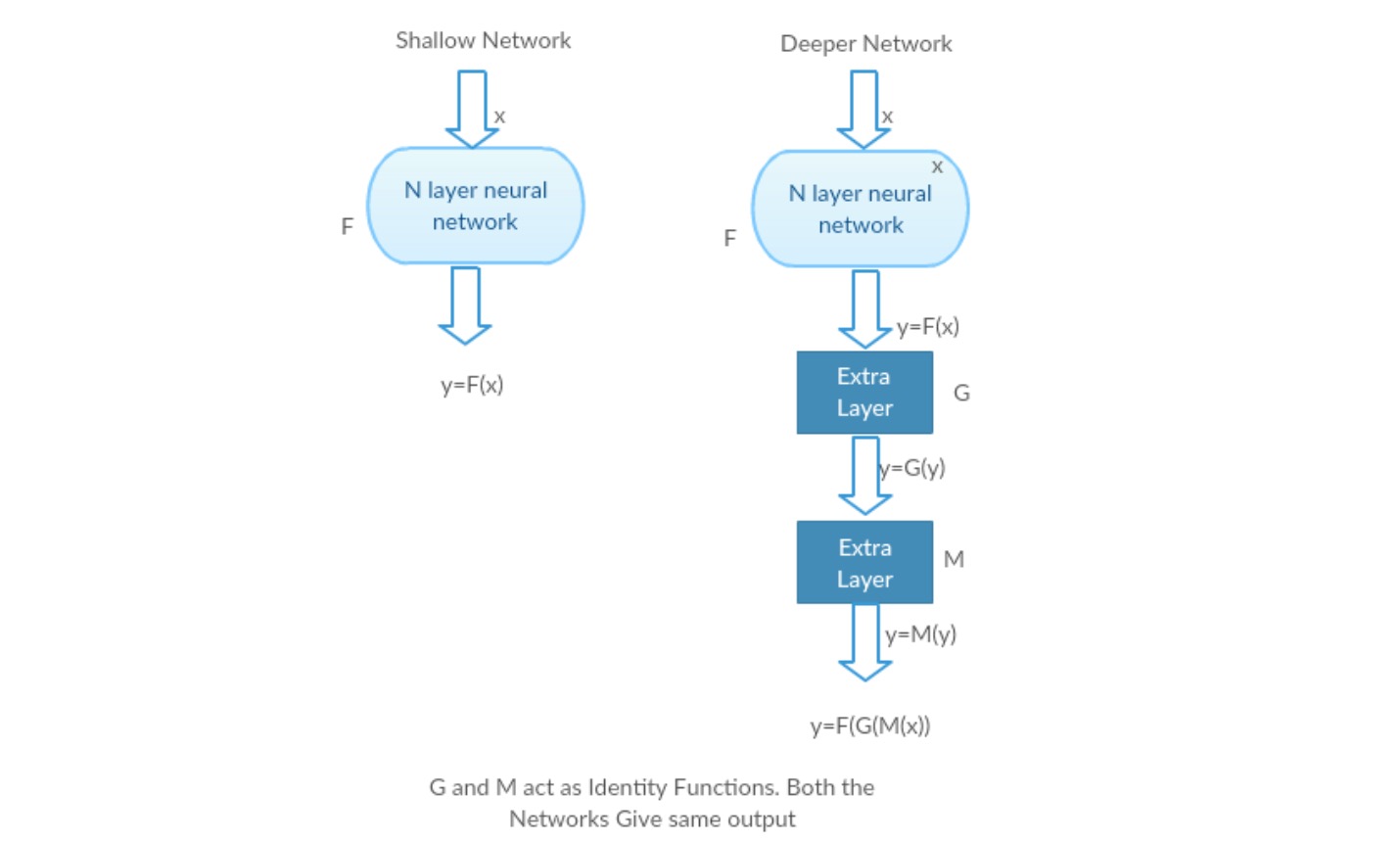
やりがいのあるシナリオ:深いネットワークでは、追加のレイヤーは、より浅いカウンタ部分よりもマッピングを近似し、誤差を大幅実験
実験
実験: 最悪の場合のシナリオでは、浅いネットワークとそれの深い変種の両方が同じ精度を与える必要があります。 やりがいのあるシナリオの場合、より深いモデルは、より浅いカウンター部分よりも優れた精度を与えるはずです。 しかし、現在のソルバーを使った実験では、より深いモデルがうまく機能しないことが明らかになりました。 そのため、より深いネットワークを使用すると、モデルのパフォーマンスが低下します。 これらの論文は,深層残留学習フレームワークを用いてこの問題を解決しようとしている。どのように解決するには?
関数(いくつかの積み重ねられた非線形層)での直接マッピングを学習する代わりに。 を使用して残差関数を定義してみましょう,に再フレーミングすることができます,ここで、および積層された非線形層と恒等関数を表します(入力=出力)そ
著者の仮説は、元の参照されていないマッピングを最適化するよりも、残差マッピング関数を最適化することが容易であるということです。
残差ブロックの背後にある直感:
恒等写像を例として見てみましょう(例えば)。 恒等写像が最適であれば、非線形層のスタックによって恒等写像()を適合させるよりも、残差をゼロ()に簡単にプッシュすることができます。 単純な言語では、非線形cnn層のスタックを関数として使用するのではなく、解決策を考え出すのは非常に簡単です(それについて考えてください)。 したがって、この関数は著者が残差関数と呼んだものです。p>
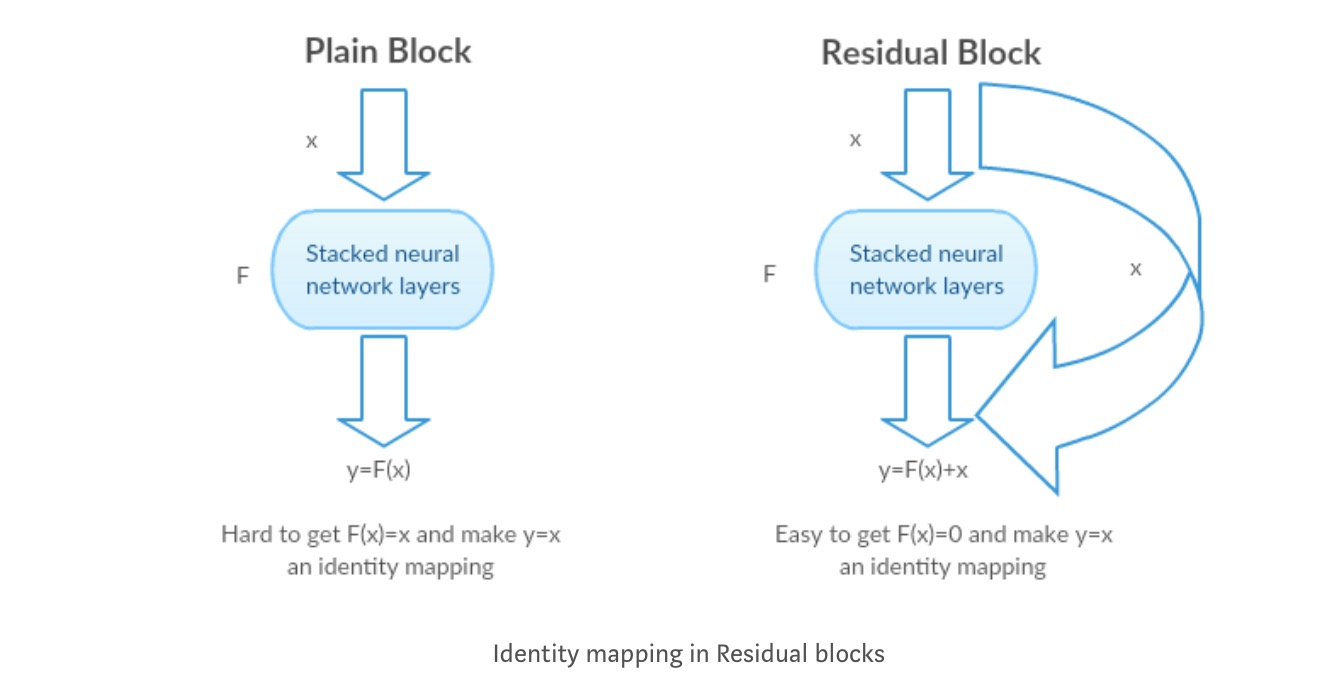
著者は彼らの仮説をテストするためにいくつかのテストを行いました。 今それらのそれぞれを見てみましょう。
テストケース:
プレーンネットワーク(VGG kind18layer network)(Network-1)とそれのより深い変種(34層、Network-2)を取り、ネットワーク-2(残留接続を持つ34層、Network-3)に残留層を追加します。
ネットワークの設計:
- 主に3*3のフィルタを使用します。
- stride2を持つCNNレイヤーでダウンサンプリング。
- グローバル平均プーリング層と最終的にSoftmaxと1000ウェイ完全に接続された層。idショートカット()は、input()とoutput()が同じ次元の場合に直接使用できます。
II.次元が変更された場合、a)ショートカットは引き続きidマッピングを実行し、余分なゼロエントリは次元が増加して埋められます。 B)投影ショートカットは、次の式を使用して次元を一致させるために使用されます(1*1convで行われます)
Results
18層ネットワークは34層ネットワークの部分空間にすぎませんが、それでも優れたパフォーマンスを発揮します。 ResNetは、ネットワークが深い場合にはかなりのマージンで優れています
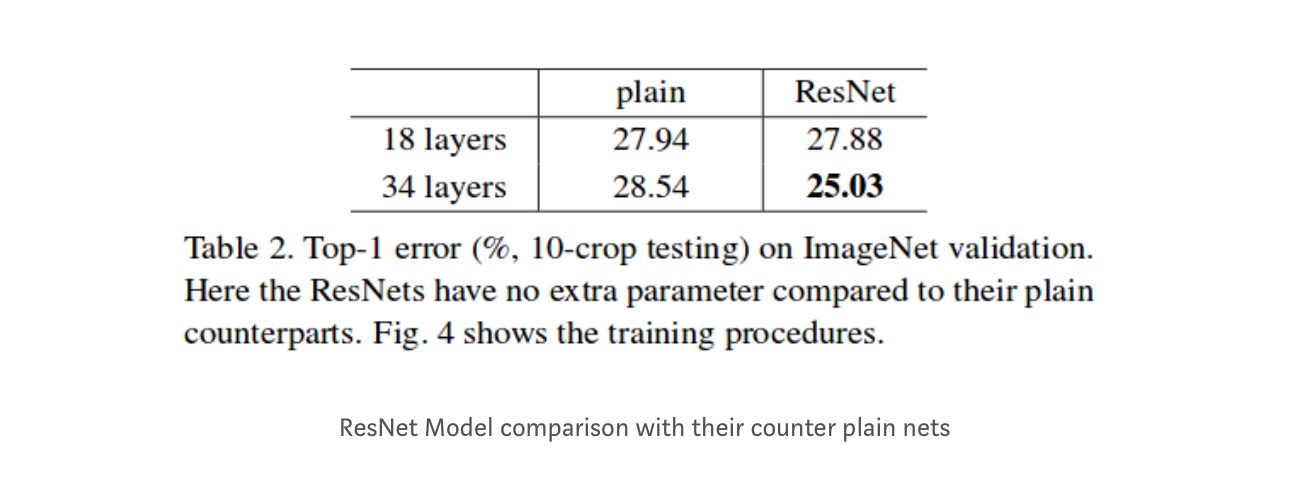
より深い研究
さらに、より多くのネットワークが研究されています。

各ResNetブロックは、2層の深さ(ResNetのような小さなネットワークで使用される)である。18、34)または3層の深さ(resnet50、101、152)。
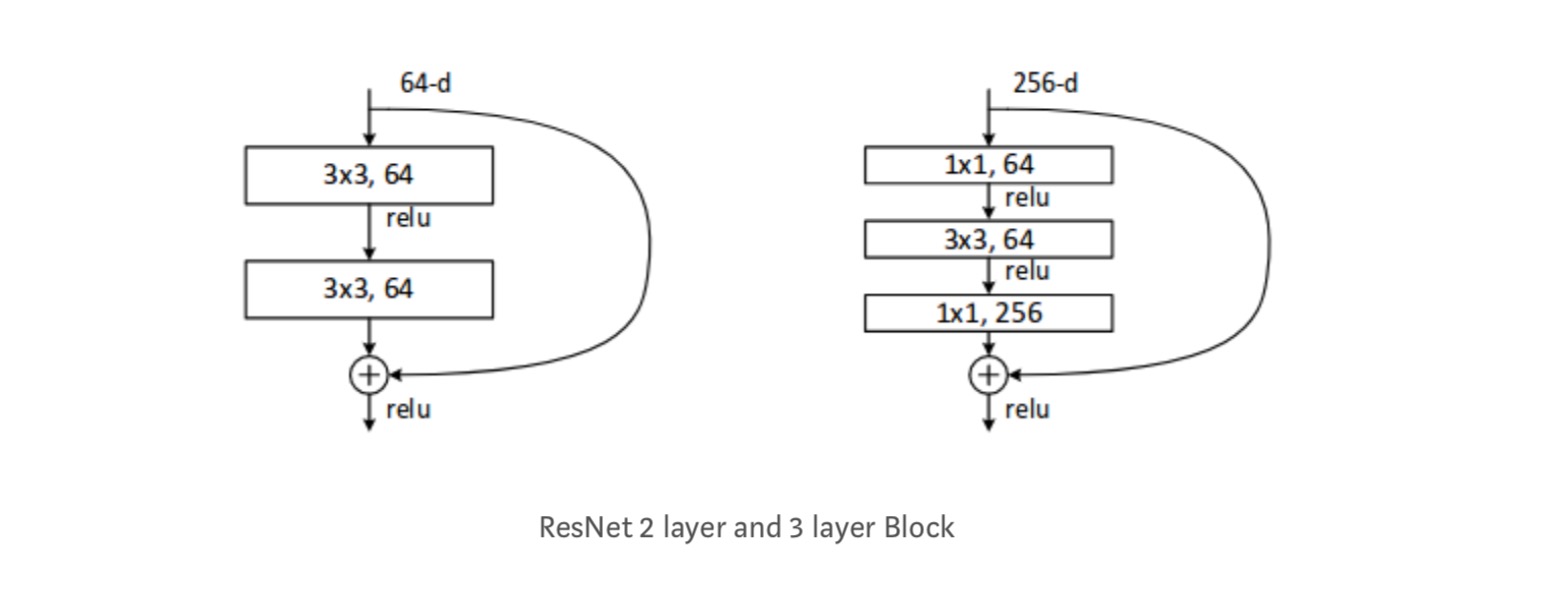
観測
- ResNetネットワークは、それのプレーンなカウンタ部分に比べて速く収束します。
- アイデンティティ対投影shorcuts。 すべての層で投影ショートカット(式-2)を使用して非常に小さな増分ゲイン。 したがって、すべてのResNetブロックは、寸法が変更されたときにのみ使用される投影ショートカットを使用して、Idショートカットのみを使用します。
- ResNet-34は、BN-inceptionおよびVGGよりも5.71%優れたtop-5検証エラーを達成しました。 ResNet-152は、トップ5の検証エラー4.49%を達成します。 深さの異なる6つのモデルのアンサンブルは、top-5の検証誤差3.57%を達成します。 ILSVRC-2015で1位を獲得
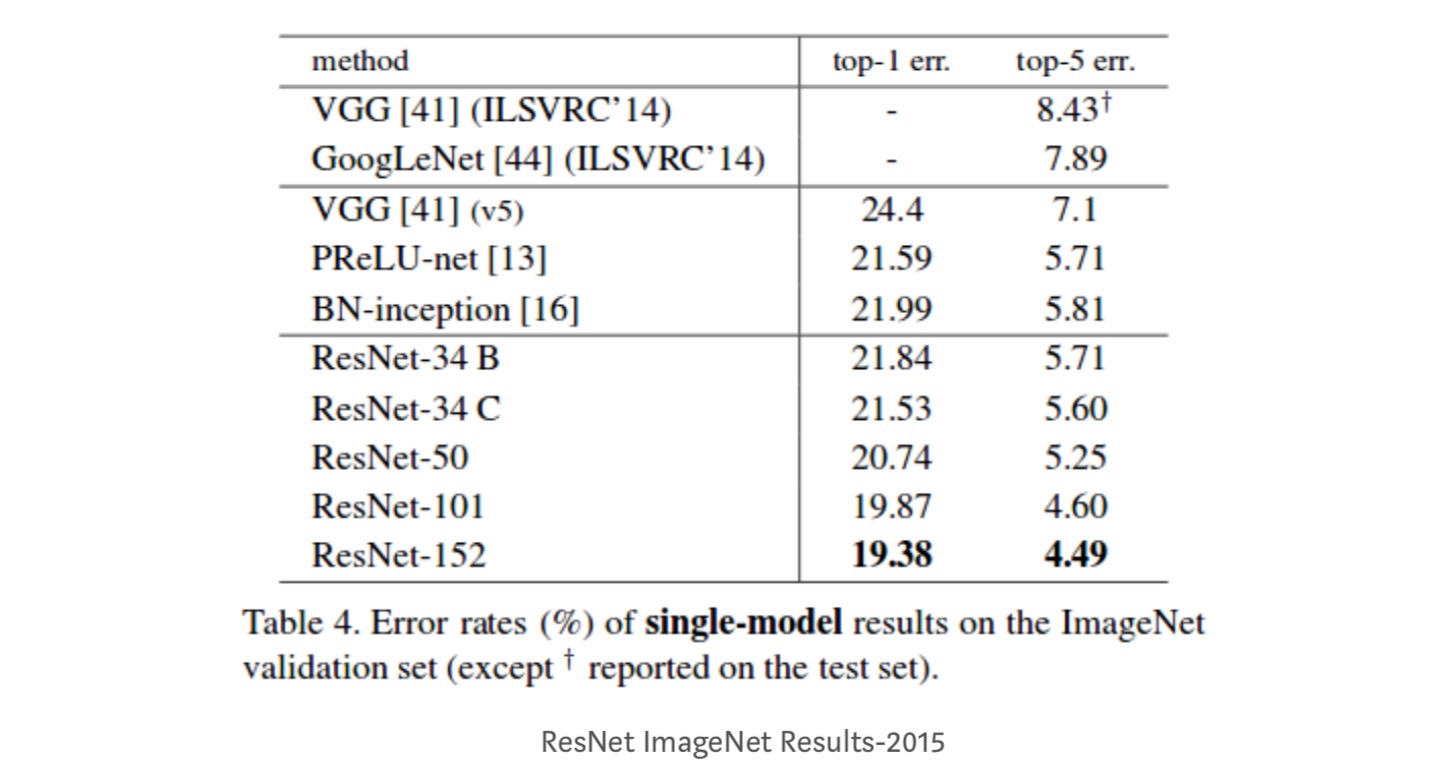
深い残差ネットワークにおけるアイデンティティマッピング
この論文では、残差ネットワークに消失勾配問題が存在しない理由と、同一性マッピング(x)を異なる関数に置き換えることによって、スキップ接続(スキップ接続は入力orを意味する)の役割について理論的に理解しています。
はじめに
深い残差ネットワークは、多くの積み重ねられた”残差単位”で構成されています。 各ユニットは、一般的な形式で表すことができます:
ここで、およびはユニットの入力と出力であり、残差関数です。
ここで、およびはユニットの入力と出力であり、残差関数です。 最後の論文では、恒等写像であり、ReLU関数である。
ResNetsの中心的なアイデアは、恒等写像を使用する重要な選択肢を持つ、に関して加法的残差関数を学ぶことです。 これは、idスキップ接続(”ショートカット”)を接続することによって実現されます。
本論文では、残差単位内だけでなく、ネットワーク全体を介して情報を伝播するための”直接”パスを作成することに焦点を当てて、深い残差ネットワークを解析します。 この導出により,両方が同一写像であれば,信号は前方および後方の両方のパスにおいて,あるユニットから他のユニットに直接伝播できることが明らかになった。 この実験は,アーキテクチャが上記二つの条件に近いと,一般的に訓練が容易になることを経験的に示した。
スキップ接続の役割を理解するために、我々は分析し、様々なタイプを比較します。 我々は、最後の論文で選択された同一性マッピングは、スケーリング、ゲーティング、および1×1畳み込みのスキップ接続は、すべてのより高い訓練損失と誤差 これらの実験は、”クリーンな”情報経路を維持することが最適化を容易にするのに役立つことを示唆している。恒等写像を構築するために,活性化関数(ReluおよびB n)を,従来の”活性化後”の知恵とは対照的に,重み層の”活性化前”と見なす。 このような観点から、次の図に示す新しい残差ユニットの設計が可能になります。 この単位に基づいて、私達は訓練し大いに易く、元のResNetよりよく一般化するCIFAR-10/100の競争の結果を1001層のResNetと示します。 我々はさらに、最後の論文の対応がオーバーフィットし始める200層ResNetを使用してImageNetの改善された結果を報告します。 これらの結果は、現代の深層学習の成功の鍵であるネットワークの深さの次元を利用する余地があることを示唆している。
深い残留ネットワークの分析
最後の論文で開発されたResnetは、同じ接続形状のビルディングブロックを積み重ねるモジュール化 本稿では、これらのブロックを”残差単位”と呼びます。 最後の論文の元の残差ユニットは、次の計算を実行します。
ここでは、-番目の残差ユニットへの入力フィーチャです。 は、-番目の残差単位に関連付けられた重み(およびバイアス)のセットであり、残差単位内の層の数である(最後の紙では2または3である)。 残差関数eを表します。g.、最後の論文の2つの3×3畳み込み層のスタック。 この関数は要素単位の加算後の演算であり、最後の論文ではReLUです。 この関数は、identity mapping:として設定されます。
も恒等写像であれば、次を得ることができます:
再帰的に:
任意のより深い単位と任意の浅い単位に対して。 この方程式はいくつかの優れた特性を示す。 (1)任意の深い単位の特徴は、任意の浅い単位の特徴に加えて、の形で残差関数として表すことができます,モデルは、任意の単位との間の残差方式であ (2)任意の深い単位の特徴は、先行するすべての残差関数(プラス)の出力の合計です。 これは、特徴が一連の行列-ベクトル積である「プレーンネットワーク」とは対照的です(BNとReLUは無視します)。
上の式はまた、素敵な後方伝搬特性につながります。 損失関数を次のように示します。
上の式は、勾配が二つの加法的項に分解できることを示しています: その用語は、任意の重み層に関係なく直接情報を伝播し、その別の用語は、重み層を介して伝播する。 上の式はまた、一般に、ミニバッチ内のすべてのサンプルに対して用語が常に-1になるとは限らないため、ミニバッチに対して勾配がキャンセルされることはまずないことを示唆しています。 これは、重みが任意に小さい場合でも、層の勾配が消失しないことを意味する。
上記の二つの式は、信号が前方および後方の両方の任意のユニットから別のユニットに直接伝播できることを示唆しています。 上の最初の2つの方程式の基礎は、(1)idスキップ接続、および(2)idマッピングである条件の2つのidマッピングです。
アイデンティティスキップ接続の重要性
のは、簡単な変更を考えてみましょう,,アイデンティティのショートカットを破るために:
ここで、変調スカラです(簡単にするために、我々はまだアイデンティティであると仮定します). この定式化を再帰的に適用すると、上記の式と同様の式が得られます:
ここで、表記法はスカラーを残差関数に吸収します。 同様に、次の形式の逆伝播があります。
前の式とは異なり、この式では、最初の加法項は因子によって変調されます。
前の式とは異なり、この式では、最初の加法項は因子によって変調されます。 非常に深いネットワーク(大きい)では、すべての場合、この因子は指数関数的に大きくなり、すべての場合、この因子は指数関数的に小さくなり、消失し、ショートカ これにより、実験で示したように最適化が困難になります。
上記の分析では、元のidスキップ接続は単純なスケーリングに置き換えられます。 スキップ接続がより複雑な変換(ゲーティングや1×1畳み込みなど)を表す場合、上の式では最初の項はwhereの導関数になります。 この製品はまた、以下の実験で目撃されたように、情報の伝播を妨げ、訓練手順を妨げる可能性があります。
スキップ接続の実験
CIFAR-10上の110層ResNetを実験します。 この非常に深いResNet-110に54の二層の残りの単位があり(3×3つの畳み込み層から成っている)、最適化のために挑戦している。 さまざまなタイプのスキップ接続が実験されています。 次の図を参照してください。
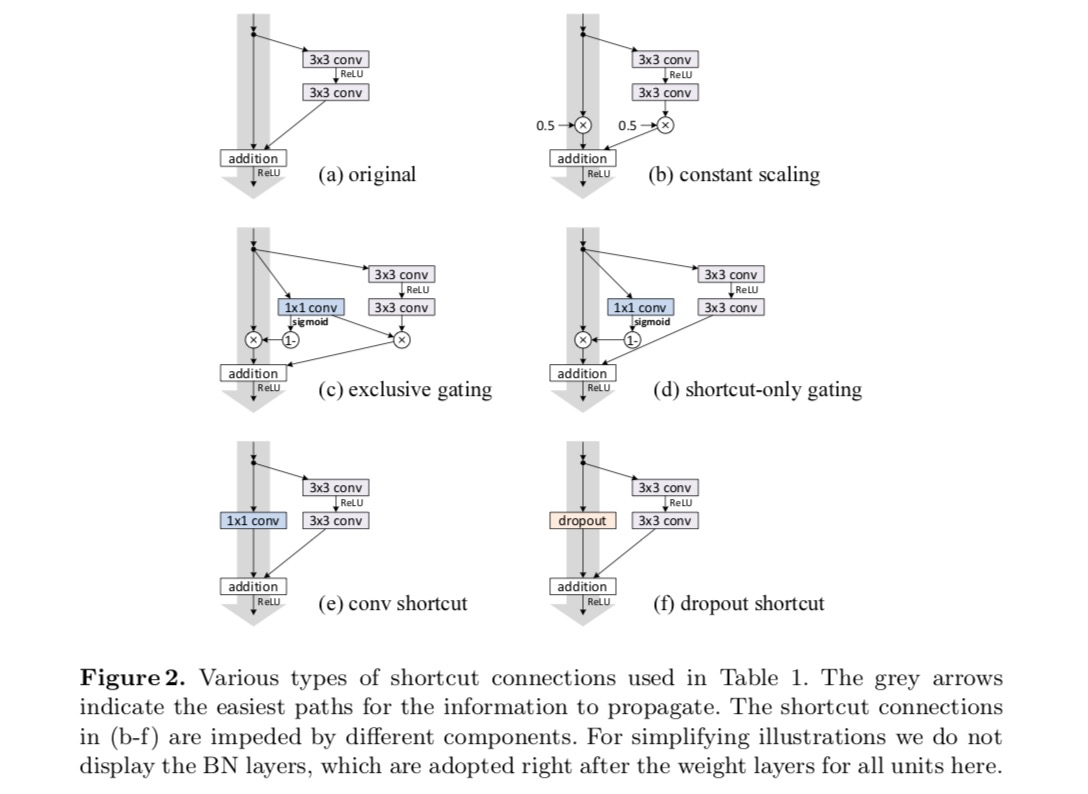
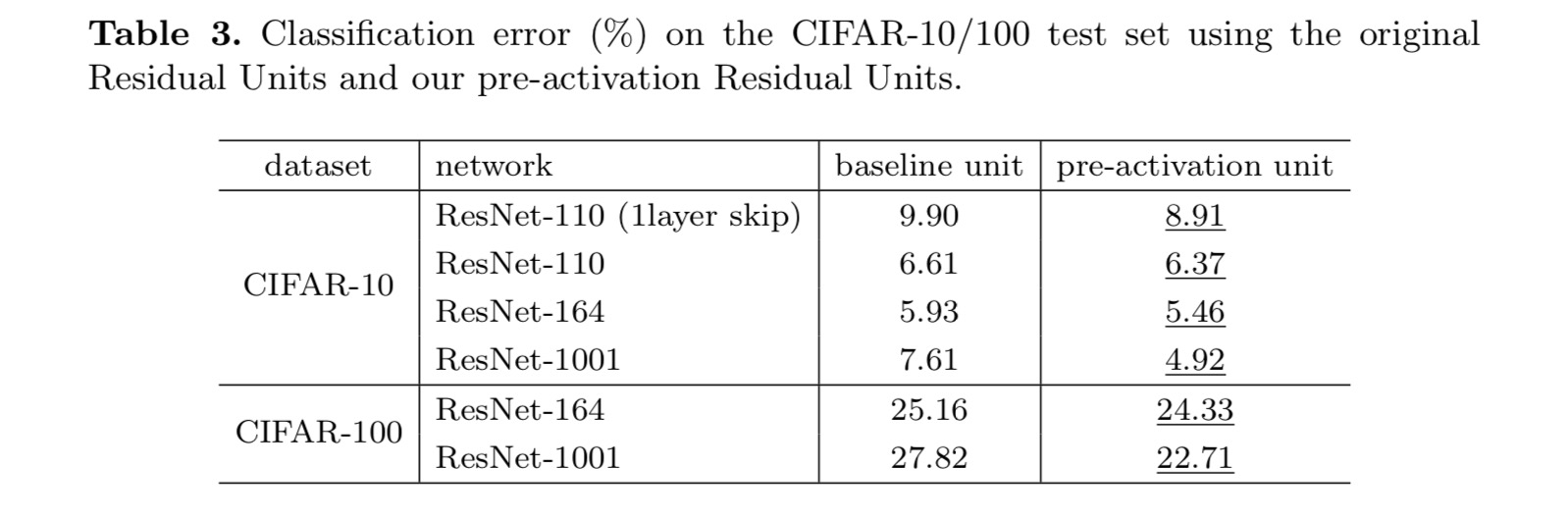
分類結果は次の表に表示されます。
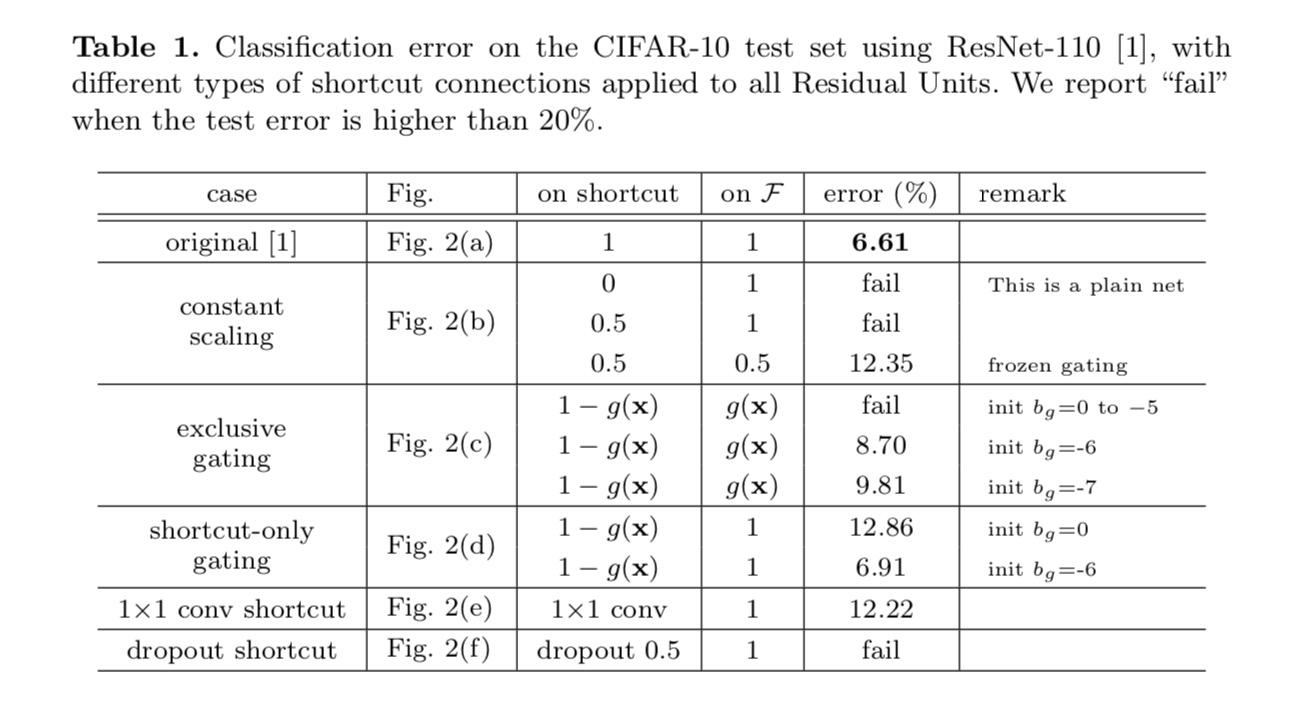
上の図の灰色の矢印で示されているように、ショートカ ショートカットの乗法操作(スケーリング、ゲーティング、1×1畳み込み、ドロップアウト)は、情報の伝播を妨げ、最適化の問題につながる可能性があります。
ゲーティングと1×1畳み込みショートカットは、より多くのパラメータを導入し、恒等ショートカットよりも強い表現能力を持つ必要があることは注目 実際、ショートカットのみのゲーティングと1×1畳み込みは、恒等式ショートカットの解空間をカバーします(すなわち、恒等式ショートカットとして最適化することができます)。 しかし,それらの訓練誤差はアイデンティティショートカットのそれよりも高く,これらのモデルの劣化は表現能力ではなく最適化の問題によって引き起こされることを示している。
活性化関数の使用法
上記のセクションの実験は、加算後の活性化が同一性マッピングであるという仮定の下にあります。 しかし、上記の実験では、最初の論文で設計されたようにReLUです。 次に、我々はの影響を調査します。
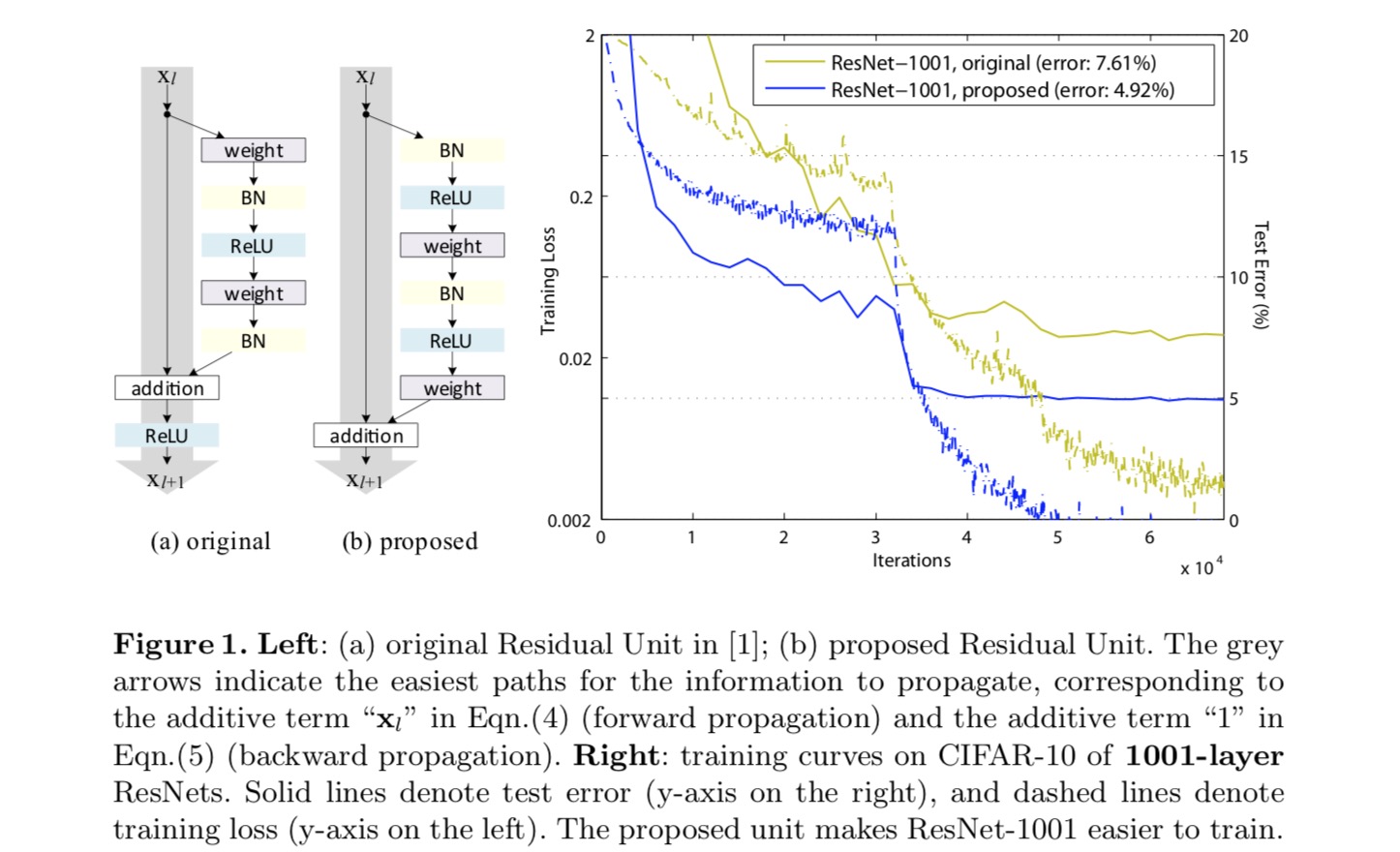
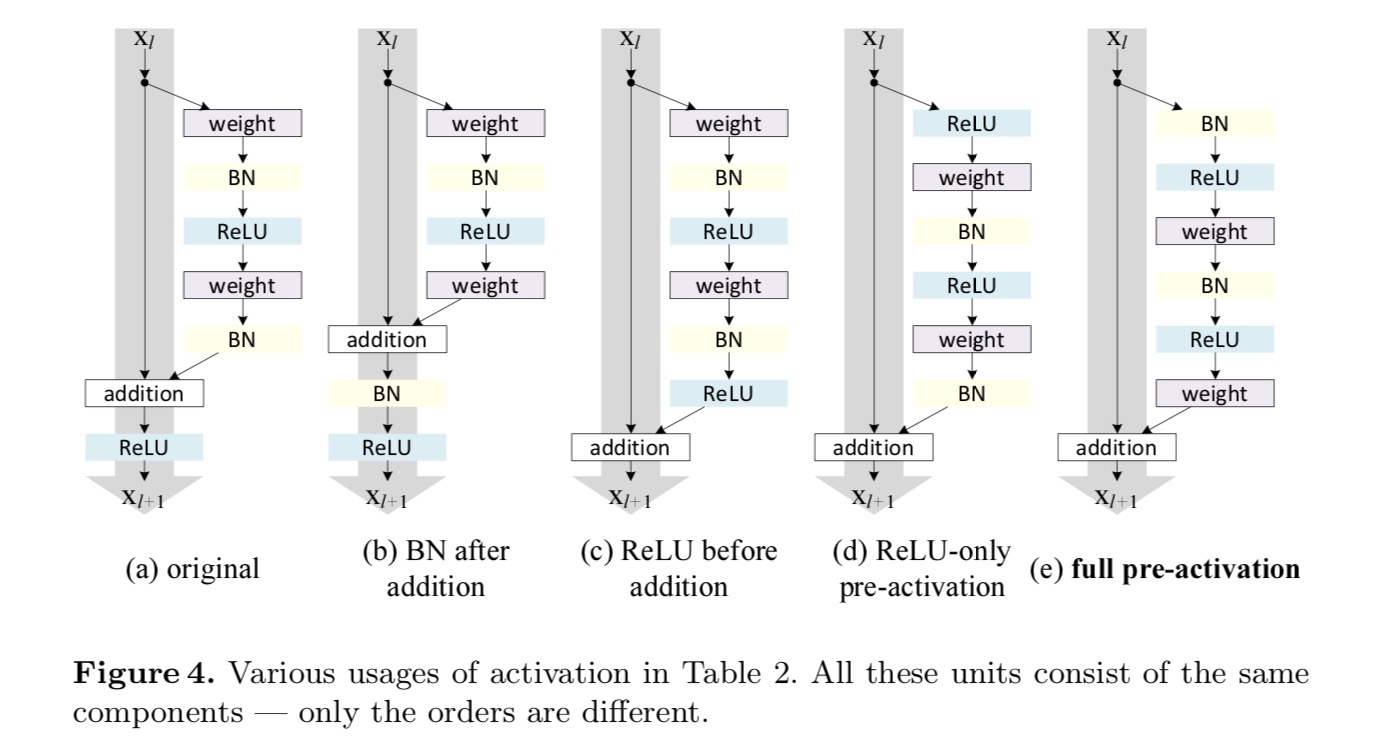
活性化関数(ReLUおよび/またはBN、バッチ正規化)を再配置することによって行われるアイデンティティマッピングを作成したいと考えています。 次の図では、最後の用紙の元の残差単位は図の形状をしています。 なお、図4(a)−bnは、各重み層の後に用いられ、残差単位の最後のReluが要素単位加算(=Relu)後であることを除いて、Bnの後にReluが採用される。 図1.1.1. 図4(b-e)は、我々が調査した代替案を示す。
活性化に関する実験
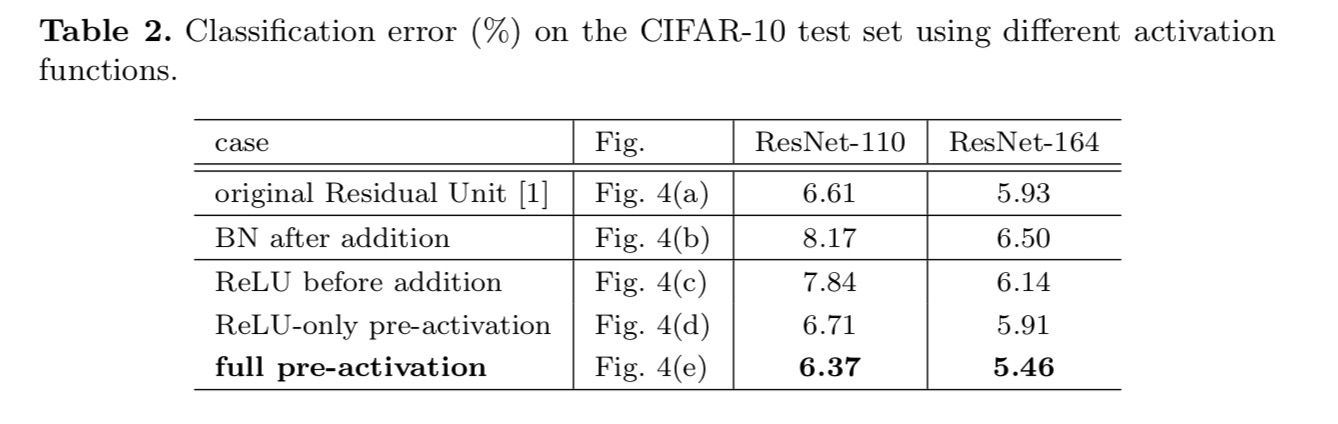
このセクションでは、ResNet-110と164層のボトルネックアーキテクチャ(ResNet-164と表記)を実験します。 ボトルネック残差ユニットは、寸法を低減するための1×1層、3×3層、および寸法を復元するための1×1層からなる。 最後の論文で設計されているように、その計算の複雑さは、2つの3×3残差単位に似ています。
活性化後または活性化前?
元の計画では、活性化は次の残差単位の両方のパスに影響します: . 次に、活性化が任意のパスにのみ影響する非対称形式を開発します。 表記法の名前を変更することにより、次の形式が得られます。
上の式のように、この新しい残差単位については、新しい加算後活性化は恒等写像にな この設計は、新しい添加後活性化が非対称的に採用される場合、それは次の残留ユニットの活性化前として再キャストすることと同等であることを これを次の図に示します:
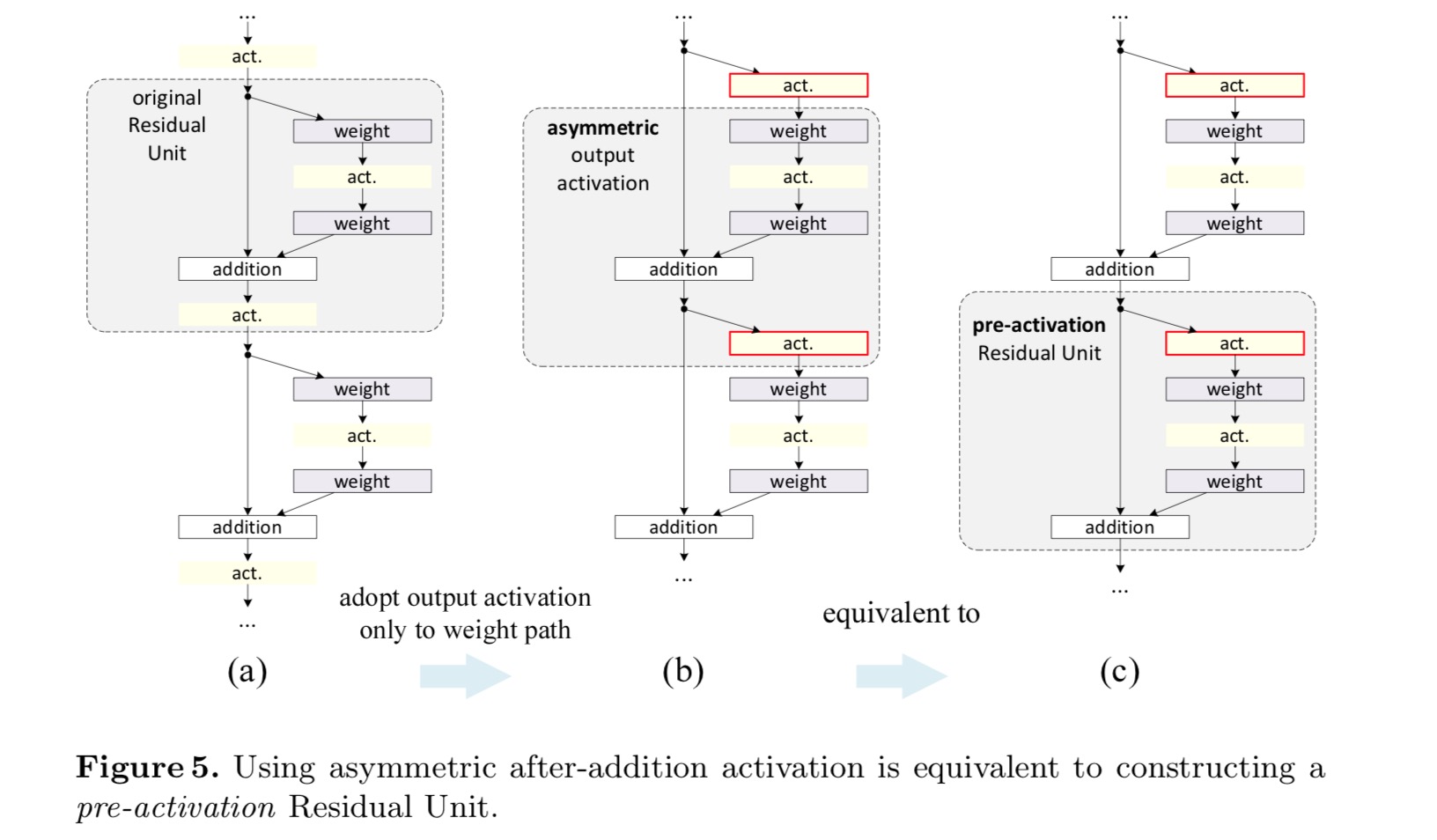
ポストアクティベーション/プリアクティベーションの区別は、要素ごとの加算の存在によって引き起こされます。 N層を持つプレーンなネットワークの場合、N−1活性化(BN/ReLU)があり、それらを活性化後または活性化前と考えるかどうかは問題ではありません。 しかし、加算によってマージされた分岐層のために、活性化の位置が重要です。 アクティベーションのさまざまな使用法を図4に示します。
このような2つのデザインを試してみます。
: (1)ReLUだけ前活発化および(2)BNおよびReLUが両方とも重量の層の前に採用される完全な前活発化。 どういうわけか驚くべきことに、BNとReLUの両方が活性化前として使用されると、結果は健全なマージンによって改善されます
私たちは、活性化前の影 まず、fはアイデンティティマッピングであるため、最適化がさらに緩和されます(ベースラインResNetと比較して)。 第二に、事前活性化としてBNを使用すると、モデルの正則化が改善されます。
結論
この論文では、深い残留ネットワークの接続メカニズムの背後にある伝播定式化を調査します。 この導出は,情報伝達を円滑にするためには,アイデンティティショートカット接続とアイデンティティ付加後活性化が不可欠であることを示唆している。 アブレーション実験は我々の導出と一致しているphenom-enaを示しています。 我々はまた、簡単に訓練し、改善された精度を達成することができる1000層の深いネットワークを提示します。
深いニューラルネットワークのための集約残差変換
はじめに
視覚認識に関する研究は、”特徴工学”から”ネットワーク工学”への移行を 人間の努力は、表現を学習するためのより良いネットワークアーキテクチャを設計する
アーキテクチャの設計は、特に多くの層がある場合、ハイパーパラメータの数が増えるにつれてますます困難になります。 VGG網は非常に深いネットワークを組み立てる簡単でけれども有効な作戦を表わす:同じ形のブロックを積み重ねる。 この戦略は、同じトポロジのモジュールをスタックするResnetによって継承されます。 この単純な規則はハイパーパラメータの自由選択を減少させ,深さはニューラルネットワークにおける本質的な次元として露出している。 さらに,このルールの単純さは,ハイパーパラメータを特定のデータセットに過度に適応させるリスクを減らす可能性があると主張した。 VGGネットとレスネットのロバスト性は,様々な視覚認識タスクと音声と言語を含む非視覚タスクによって証明されている。
VGG-netsとは異なり、インセプション-モデルのファミリは、慎重に設計されたトポロジーが理論的な複雑さが低く説得力のある精度を達成できることを インセプション-モデルは時間の経過とともに進化してきましたが、重要な共通の特性は分割変換マージ戦略です。 Inceptionモジュールでは、入力はいくつかの低次元埋め込み(1×1畳み込み)に分割され、特殊なフィルタのセット(3×3、5×5など)によって変換されます。)、および連結によってマージされます。 インセプション-モジュールの分割-変換-マージ挙動は,大きくて緻密な層の表現力に近づくが,計算の複雑さはかなり低いと予想される。
精度が良いにもかかわらず、インセプション-モデルの実現には一連の複雑な要因が伴っています。 これらのコンポーネントの慎重な組み合わせは優れたニューラルネットワークレシピをもたらすが、特に設計する多くの要因とハイパーパラメータがある場合、インセプションアーキテクチャを新しいデータセット/タスクに適応させる方法は一般的に不明である。
本稿では、vgg/ResNetsの繰り返し層戦略を採用し、split-transform-merge戦略を簡単に拡張可能な方法で利用する簡単なアーキテクチャを提示します。 このネットワーク内のモジュールは,それぞれが低次元埋め込み上で一連の変換を実行し,その出力は総和によって集約される。 私たちは、このアイデアの単純な実現を追求します—集約される変換はすべて同じトポロジーです。 この設計は私達が専門にされた設計なしであらゆる多数の変形に拡張することを可能にする。
計算の複雑さとモデルサイズを維持するという制限された条件下であっても、集計された変換が元のResNetモジュールよりも優れていることを経験的に 我々は、容量を増やすことによって精度を高めることは比較的容易であるが(より深くまたはより広い)、複雑さを維持しながら精度を高める方法は、文献ではまれであることを強調している。
私たちの方法は、基数(変換のセットのサイズ)は、幅と深さの次元に加えて、中心的に重要な具体的で測定可能な次元であることを示しています。 実験は、特に深さと幅が既存のモデルのリターンを減少させ始めるときに、基数を増やすことは、より深くまたはより広く行くよりも精度を得るための
ResNeXtという名前のニューラルネットワーク(次の次元を示唆しています)は、ImageNet分類データセットでResNet-101/152、ResNet-200、Inception-v3、およびInception-ResNet-v2より優れています。 特に、101層のResNeXtはResNet-200よりも優れた精度を達成できますが、複雑さはわずか50%です。 さらに、ResNeXtはすべてのInceptionモデルよりもかなりシンプルなデザインを示しています。
メソッド
VGG/ResNetsに続いて高度にモジュール化された設計を採用しています。 このネットワークは残差ブロックのスタックで構成されている。 (1)同じサイズの空間マップを生成する場合、ブロックは同じハイパーパラメータ(幅とフィルタサイズ)を共有し、(2)空間マップが2倍にダウンサンプリングされるたびに、ブロックの幅に2倍に乗算されます。 第二のルールは、計算の複雑さは、フロップ(浮動小数点演算、乗算加算の#)の面で、すべてのブロックでほぼ同じであることを保証します。
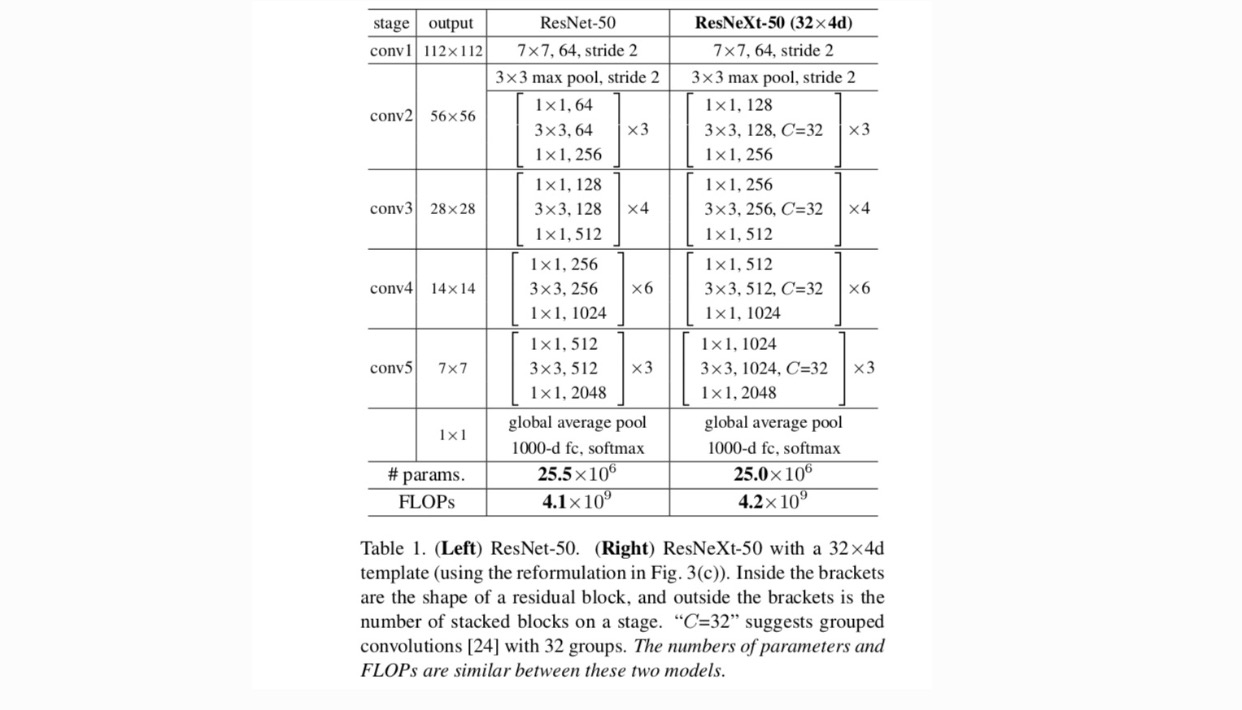
これら二つのルールでは、我々は唯一のテンプレートモジュールを設計する必要があり、ネットワーク内のすべてのモジュールは、それに応じて決定するこ だから、これら二つのルールは大幅に設計スペースを絞り込むと、私たちはいくつかの重要な要因に焦点を当てることができます。 これらのルールによって構築されたネットワークを表1に示します。
人工ニューラルネットワークにおける最も単純なニューロンは、完全に接続された畳み込み層によって行われる基本変換である内積(重上記の操作は、分割、変換、および集約の組み合わせとして再キャストできます。 (1):分割:ベクトルは低次元埋め込みとしてスライスされ、上記では単一次元部分空間である(2)変換:低次元表現は変換され、上記では単純にスケーリングされる:(3)集約:すべての埋め込みにおける変換はによって集約される。
単純なニューロンの上記の分析を考えると、基本変換(w_i、x_i)をより一般的な関数に置き換えることを検討します。 形式的には、集約された変換を次のように提示します。
ここで、任意の関数にすることができます。 単純なニューロンに類似して、(必要に応じて低次元の)埋め込みに投影し、それを変換する必要があります。
私たちは基数と呼んでいます。 はinと同様の位置にありますが、等しくする必要はなく、任意の数にすることができます。 基数は本質的な次元であり,幅と深さの次元よりも効果的であることを実験によって示した。
本稿では、変換関数を設計する簡単な方法を考えてみましょう:すべてが同じトポロジーを持っています。 これにより、同じ形状のレイヤーを繰り返すVGGスタイルの戦略が拡張されます。 個々の変換を図に示すボトルネック型アーキテクチャに設定しました。 1(右)。 この場合、それぞれの最初の1×1層は低次元埋め込みを生成する。p>
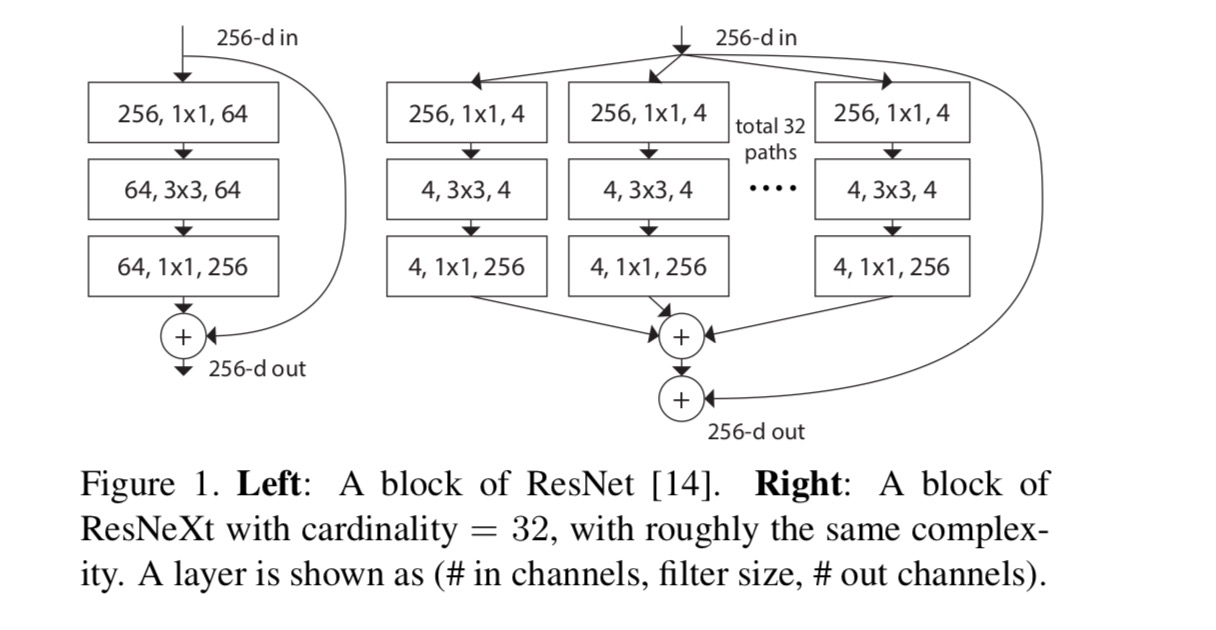
最後の方程式の集計変換は、残差関数として機能します。
ここで、出力です。
ResNeXtとInception-ResNet/Grouped-Convolutionsの関係を次の図に示します:
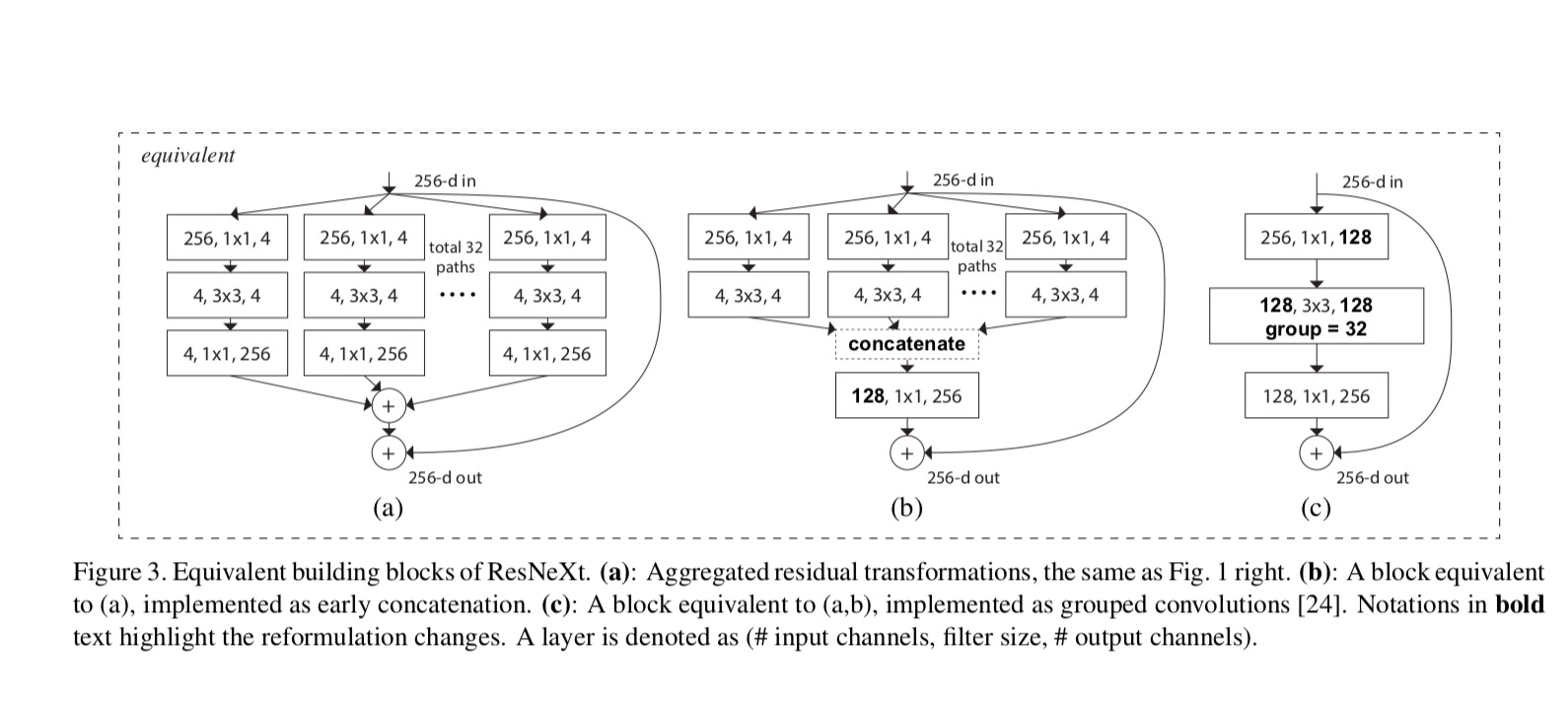
複雑さを維持しながら異なる基数を評価する場合、他のハイパーパラメータの変更を最小限に抑えたいと考えています。 ブロックの入力と出力から分離できるため、ボトルネックの幅を調整することを選択します(図1(右)の4-dなど)。 この戦略では、他のハイパーパラメータ(ブロックの深さや入力/出力の幅)に変更を加えないため、基数の影響に焦点を当てるのに役立ちます。
図中に。 図1(左)に示すように、元のResNetボトルネックブロックにはパラメータと比例フロップがあります(同じフィーチャマップサイズ上にあります)。 ボトルネック幅では、図中のテンプレート。 1(右)は、パラメータと比例フロップを持っています。 ときと、この番号。 次の表は、基数とボトルネック幅の関係を示しています。p>

実験
基数対幅。 まず、表2に記載されているように保存された複雑さの下で、基数とボトルネック幅の間のトレードオフを評価します。 その結果を表3に示す。 ResNet-50と比較すると、32×4d ResNeXt-50の検証誤差は22.2%であり、ResNetベースラインの23.9%よりも1.7%低い。 複雑さを維持しながら基数が1から32に増加すると、エラー率は減少し続けます。 さらに、32×4d ResNeXtはResNet countetpartよりも訓練誤差がはるかに低く、ゲインは正則化によるものではなく、より強い表現によるものであることを示唆しています。p>
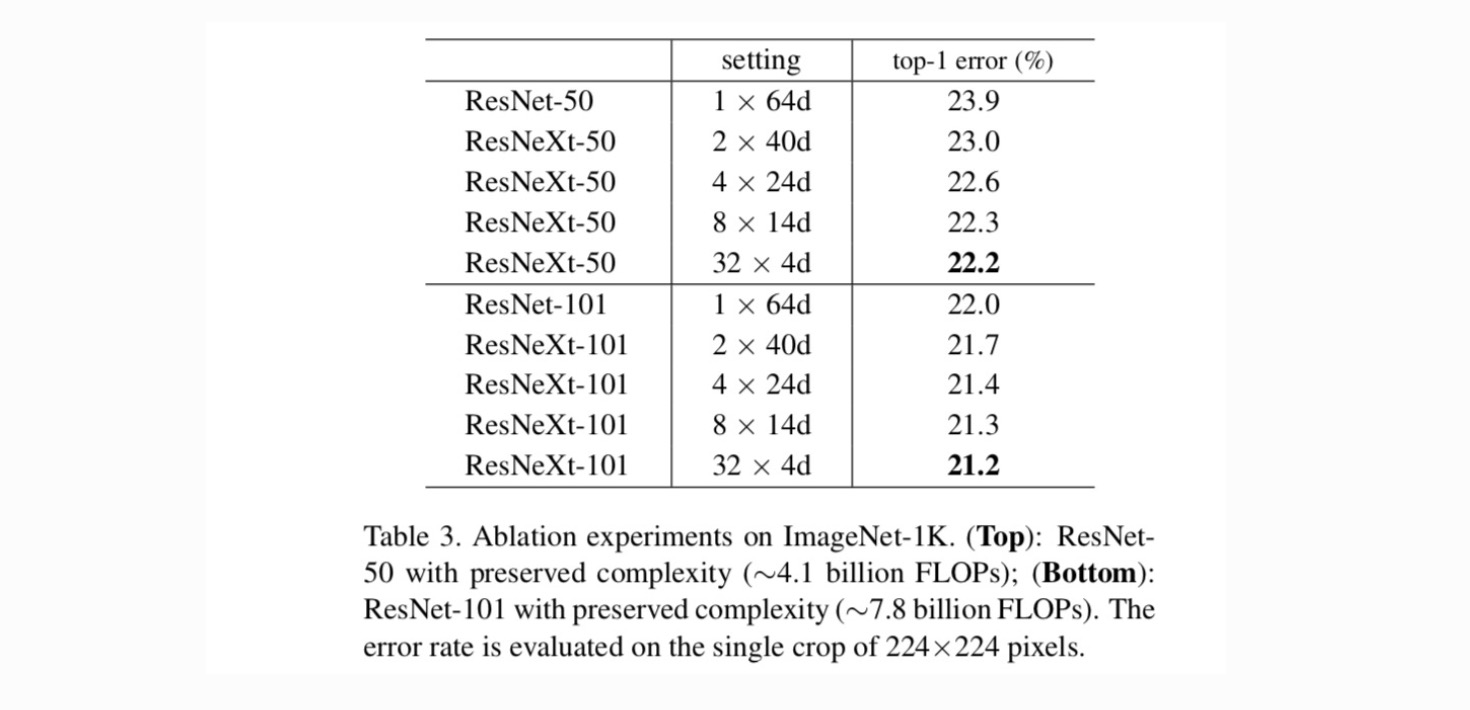
基数の増加とより深い/より広い。次に、基数Cを増やしたり、深さや幅を増やしたりすることで、複雑さの増加を調べます。 以下の亜種(1)を200層まで比較します。 私達はResNet-200を採用します。 (2)ボトルネック幅を大きくすることにより、より広く行く。 (3)cを倍増させることによって基数を増加させる
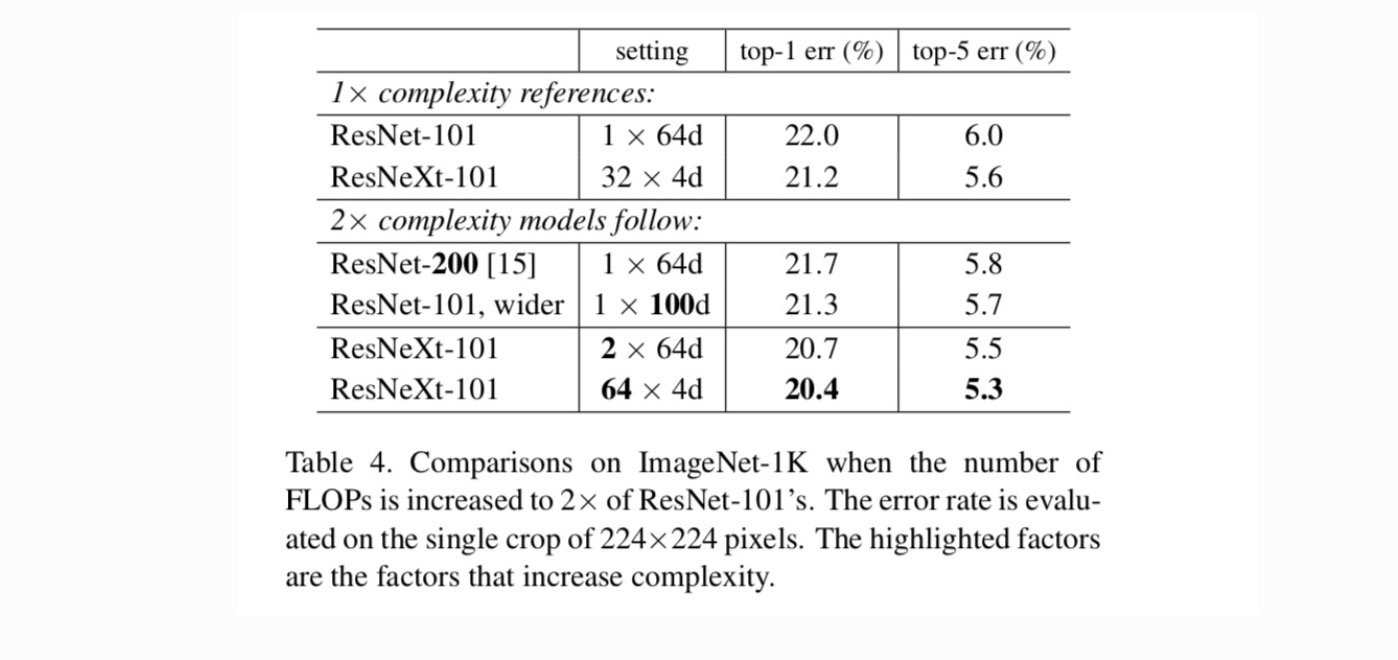
表4は、複雑さを2倍にすると、ResNet-101ベースライン(22.0%)に対して誤差が一貫して減少することを示しています。
しかし、より深く(ResNet-200、0.3%)またはより広い(より広いResNet-101、0.7%)になると、改善は小さくなります。 逆に、基数Cの増加は、より深くまたはより広く行くよりもはるかに良い結果を示します。
最先端の結果との比較。 表5に、ImageNet検証セットでのシングルクロップテストの結果を示します。 私達の結果はResNet、開始V3/v4および開始ResNet v2と好意的に比較し、4.4%の単一穀物のtop-5誤り率を達成する。 さらに、私達の建築設計はすべての開始モデルより大いに簡単で、かなり少数の超変数が手で置かれるように要求する。