投稿June2008.
測量の数学に関する2つの列の2番目(最初はここにあります)。 …
Bill Casselman
ブリティッシュコロンビア大学、バンクーバー、カナダ
cass at math.ubc.ca
John Eggers
カリフォルニア大学サンディエゴ校
jeggers at ucsd.edu
 友人にメール 友人にメール |
 この記事を印刷する この記事を印刷する |
平面計は、地域、通常は地図や写真上の不規則な領域の領域を測定するた 彼らはかつて一般的でしたが、現在は主にデジタルツールに置き換えられています。次の図は、セットアップのいくつかのアイデアを与えます。
棒の腕はテーブルで固定される棒のまわりで自由に回ります。 トレーサーアームはピボットの周りを回転し、ピボットはポーラーアームと結合します。 トレーサーを使って時計回りの曲線をトレースし、そうすると測定ホイールが転がり、それが転がる総距離がダイヤルに蓄積されます。 サポート車輪はfloppingからの事を保つ。 最後に、ダイヤルから番号を読み取り、平面計の特定の構成にのみ依存する係数で乗算した後、曲線の内側の領域を取得します。p>

次の図は、メカニズムのより良いビューを提供します。

キャリッジを車輪、ダイヤル、ピボットのアセンブリと呼びます。 次の写真では、それをよりよく見て、測定ホイールが動くにつれてダイヤルを回転させるワームドライブを見ることができます。ここでは、それを導入したJakob Amslerの記事から、元のplanimeterの図です。
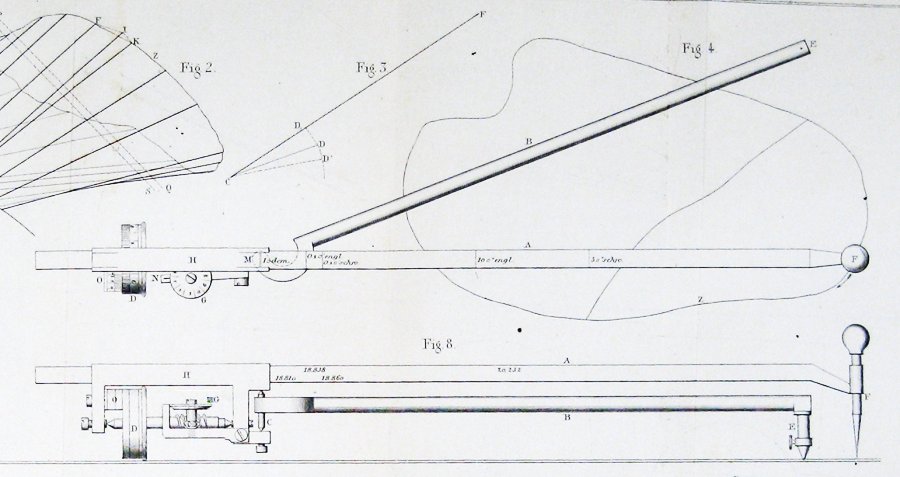
このような単純なものはどのように面積を測定できますか?
平面計の幾何学
平面計の時計回りの動きは、数学者が正の回転でなければならないと決めた方向とは反対の方向です。 この規則に違反するのではなく、私たちはこれから数学者の平面計を使って反時計回りに動くようにします。 他の数学者の空想のように、地球上には何もありません!トレースしたい曲線に対して平面計を配置する方法にはいくつかの制限があります。
トレースしたい曲線に対して平面計を配置する方法にはいくつかの制限があります。
キャリッジはトレーサアームに沿ってスライドさせることができるが、すべての場合において、トレーサアームの長さlは、ポールアームの長さrよりも小さい。 これはトレーサーが棒の間隔r-lの内で決して得ることができないことを意味する。 したがって、トレースされる曲線は、半径r-l、もう一方のr+lを持つ二つの円の間の環内になければならない。実際には、腕を完全に伸ばすべきではないことがすぐに明らかになるはずですので、トレースする曲線は完全に輪の内側になければなりません。 さらに、通常、ポールは曲線の外側に配置されます。

環内の特定の点について、その点にトレーサーを配置する平面計の正確に二つの可能な構成があります。 一方の点またはもう一方の点を選択することは、平方根の符号を選択することを意味します。 私たちはこれをplanimeterの向きを選択すると呼んでいます。 平方根が正の場合は正です。 方向が選択されると、腕が完全に拡張されない限り、それは同じままになります。 これは決して起こってはいけません。 あなたのカーブが環状の内に完全にある限り、planimeterの構成はトレーサーの道と滑らかにそして独特に変わる。
次に行うことは、測定ホイールの動きについていくつかのことを理解することです。 次の図が示すように、車輪が直線で距離Cを移動すると、車輪は角度θ=C/Rを通って回転します。Rはその半径です。したがって、ホイールの回転とトレーサーアームの移動距離が互いに何らかの関係を持っていることは本当に事実です。

したがって、ホイールの回転とトレーサーアームの移動距離が互いに何らかの関係を持っていることは本当に事実です。 しかし、この関係は少し微妙です。 腕がちょうど距離Cをまっすぐに動かすと、掃引された領域はlCになりますが、それ自体に平行にシフトすると、掃引された領域は0になります。 最初のケースでは、車輪の円周上の点は距離Cを移動します。 また、腕が斜めに移動すると、車輪は腕で覆われた平行四辺形の高度に等しい距離を回転させます。 腕がそれ自身に平行に翻訳するすべての場合では、ピボットとトレーサー間のトレーサーの腕の部分によって掃除される区域はcが車輪の回転によって測定される間隔であるlCと等しくなる。 これは測定の車輪の動きに腕の動きを関連させる基本的な事実である。

これを正確に表現する方法は、腕がどのように動いても、車輪によって測定された距離は経路積分であるということです

そして、tは進行方向を指す単位ベクトルである(例えば、腕がそれ自身に平行に動いている場合、nとtの内積は0である)。Guldinの定理
次に、planimeterの動作を直感的に明確にしようとしていますが、最初に特別な種類のplanimeterを見て、この場合より一般的な結果を証明します。 長さlの自由に動く単一のアームを取り、その中心に半径Rの測定ホイールを取り付けたとします。p>

次に、平面上で腕を動かします。 アームが動き回るときに測定ホイールがθラジアンの全角度で回転する場合、円周上の点が移動する距離はC=θ rです。
Guldin’S Theorem
グルディンの定理 この状況では、アームによって掃引された総面積は製品lCです。
ここの領域は符号で解釈されます。 腕がちょうどその中心の周りを回転すると、腕の半分が前方に移動し、もう一方が後方に移動し、二つがキャンセルされます。guldinのアサーションは、armが翻訳したばかりの場合に有効であることはすでに見てきました。
もちろん、これは常に起こるわけではありません-腕は移動するだけでなく、移動するにつれて回転するかもしれません。 しかし、掃引された領域を次のように切り刻むことで何が起こっているのかを見ることができます:
測定ホイールは腕の中央にあるため、腕が回転すると、一方の側の小さなブロックが他方の側に展開されると、一方の側の小さなブロックが押しつぶされます。 これらの効果は、正確にお互いをキャンセルします。完全に厳密な証明は、二重積分における変数の変化の式と経路積分としての車輪移動の式を使用することによって与えることができる。
ホイールがどこか別の場所に配置されているとします。 その位置がc+vここで、cは腕の中心であり、vは腕に沿ったベクトルであるとします。 Vの長さは固定されたままになります。 ホイールが続く経路はc(t)+v(t)です。 パス積分は現在
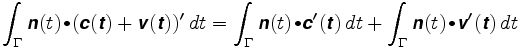
最初の積分は、ホイールが腕の中心にあった場合に移動する距離です。 第二に、ベクトルv(t)は常にnに垂直であり、v(t)は一定の長さを有する。 ベクトルv(t)は、πに等しい半径の円上を移動します。 したがって、nとv'(t)の内積はちょうどv'(t)の符号付き長さであり、第二の積分は腕の全回転のπ倍に等しい。 したがって、:
ホイールが腕の中心からの距離θにある場合、ホイールが測定する距離CはC0、ホイールが中心にある場合に測定される距離に加え、θに腕が回転する全角度θを加えたものである。あなたはすぐにその中心の周りに腕を回転させることによって、この簡単なケースを見ることができます。
これをGuldinの定理と組み合わせると、すべての場合にそれがわかります:
c=C0+ρ θ
area Sweeped out=l c0=l c-l ρ θ
完全な結果
guldinの式は、符号付き領域を与えます-あなたが領域の上に後方に掃引すると、ホイールが後方に行き、あなたがすでにカバーしている領域をキャンセルします。 これをフリーアームが開始した場所に正確に戻ってくる場合に適用すると、lCはアームの右端から左のアームによって掃引された領域の面積を引いた閉じた領域の面積に等しいことがわかります。
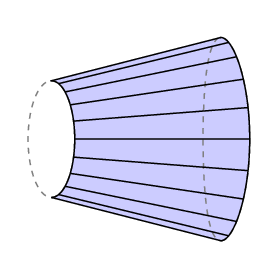
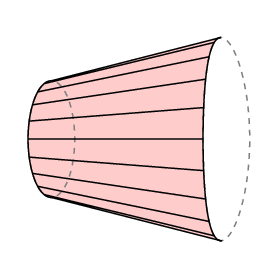

極平面計の場合、アームの底部は極を中心とする半径rの円の円弧に制限されているため、L Cはトレーサ….. さらに、通常、極は測定される領域の外側にあり、この場合、アームの総回転量は0でなければならない。 したがって、この場合、我々は持っています
area of the region traced=lC
ここでは、彼が発明した楽器に関する彼の元の論文でJakob Amsler、発明者によって含まれる図です。
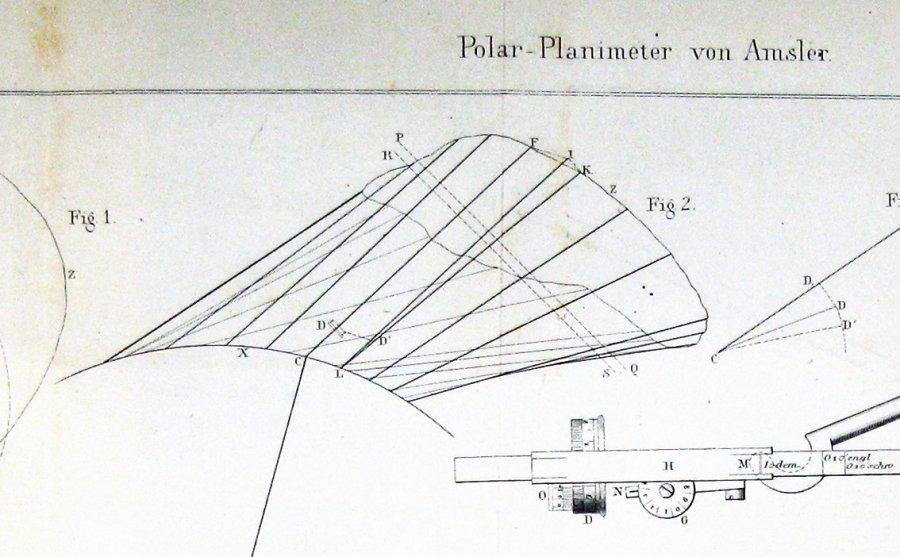
Amslerが何らかの形のGuldinの定理によって彼の構造を導いたことはかなり明らかです。
平面計とグリーンの定理
すでに述べたように、平面計の向きを選択したので、平面計の構成はトレーサ位置の連続関数です。 正の方向を選択したとします。 次に、環の各点に単位ベクトルnを付けることができ、これはトレーサーでトレーサーアームに反時計回りに垂直なものです。
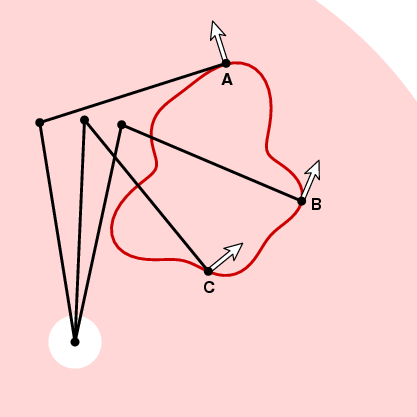
測定ホイールが次の瞬間に曲線に沿った動きにどのように応答するかは、このベクトルと曲線の単位接線ベクトルとの間の角度に 上の写真のAでは、曲線に沿った動きがトレーサーアームに平行であるため、測定ホイールは移動しません。 Bでトレーサーが小さい間隔dsを動かせば、従って測定の車輪は。 そしてcで測定の車輪は0とdsの間で間隔を動かします。 正確には、tが曲線のある点での単位接線ベクトルであると仮定します。 トレーサが曲線に沿って距離dsを移動すると、その時点で測定ホイールは距離d dsを移動します。d=n。 言い換えれば、曲線Θの周りをすべて移動すると、測定ホイールはnの積分に等しい総距離を移動します。 t ds(dot product),or

しかし、環のすべての点は平面計の一意の正の配置に対応するので、環のすべての内部点にベクトルnを割り当てることができ、したがってベクトル場を定義する。 曲線Γはその内部Ωの境界であり、我々の仮定の一つによって、これはnが定義されている領域に完全に含まれています。 グリーンの定理は、この領域の境界の周りの経路積分もΩ上のある積分に等しいことを示しています: したがって、
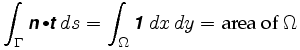
より正確には、グリーンの定理は、
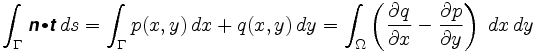
ここで、n=は関与するベクトル場です。 二重積分における被積分関数はベクトル場のカールと呼ばれる。p>
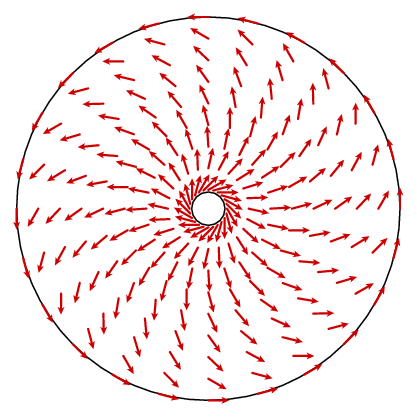
これは非常に遠くに私たちを取得していないようです。 何が起こるべきかは、カールが定数1であるということです。 原理的には、ベクトル場nの式を見つけてそのカールを計算することができますが、それはあまり啓発的ではありません。 しかし、私たちは別の事実を利用することができます。 ベクトル場は円形の対称性を持ち、これはそれが1つの半径上にあるものによって決定されることを意味する。 余弦則は円周成分の簡単な公式を与える。
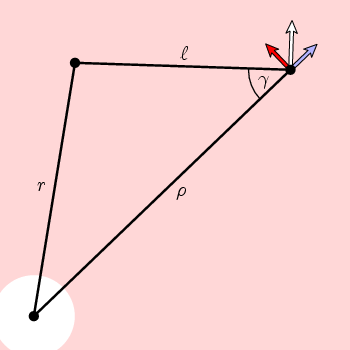
この図の単純な幾何学から、nの円周成分は
f(π)=cos(π)=(π2+l2-r2)/(2π l)
グリーンの定理の本当のポイントは、被積分関数が1であることを確認するためには、適切な小さなパスの周りのパス積分がエリア。 このために、私たちはここのように私たちの地域を選択します:
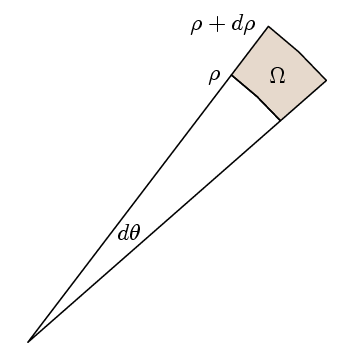
l回の経路積分は
l(ρ+dp)(f(ρ+dp-f(ρ))dθ
または
(θ/2)((ρ+dp)2-ρ2)
する領域の面積Ω.
他の種類の平面計
Guldinの定理は、測定ホイールを持つアームが曲線をトレースするが、一方の端が一次元曲線に制限されているときはいつでも、測定ホイールの動きがトレーサーによってトレースされた領域を伝えることを意味する。 これは、例えば、ピボットが圧延シリンダーにあることによって直線に制限される圧延のplanimeterと起こる。p>

詳細を調べるには
-
 まだplanimetersを作り、販売しています。
まだplanimetersを作り、販売しています。 - 微分および積分微積分ボリュームII、R.クーラント、ブラッキー&息子、1936。 Guldinの公式のセクション(pp.294-298)は、平面計がどのように機能するかについての説明を提供しています。
- アムスラーの元の記事、Vierteljahresschrift der Naturforschenden Gesellschaft In Zuerich、1856。 これは図が欠落していますが、彼らはここにあります:
- Amslerの最初の図
- Amslerの第二の図
記事を見つけてくれたStony Brook大学図書館のDonna Sammisと、図の写真を提供してくれた夫のRobertに感謝します。
アムスラーが設立した会社は、20世紀に入っても楽器を生産していました。 この写真は、プラニメーターのパンタグラフバージョンのロゴを示しています。

- “プラニメーターについて”EngineerSupply。 同社はまた、YouTubeにビデオを投稿しています。
Bill Casselman
ブリティッシュコロンビア大学、バンクーバー、カナダ
cass at math.ubc.ca
John Eggers
カリフォルニア大学サンディエゴ校
jeggers at ucsd.edu
JSTORにアクセスできる人は、上記の論文のいくつかを見つけることができます。 アクセス権を持つ人のために、アメリカ数学会のMathSciNetは、追加の書誌情報といくつかのこれらの材料のレビューを取得するために使用することができま 上記の項目のいくつかは、書誌サービスも提供するACMポータルを介してアクセスできます。