フランク-コンドン原理は、振動遷移の強度、または光子の吸収または放出を記述する。 それは、分子がイオン化のような電子遷移を受けているとき、分子の核配置は有意な変化を経験しないと述べている。 これは、核が電子よりもはるかに巨大であり、電子遷移が核が応答できるよりも速く起こることによるものである。 核が新しい電子配置で再調整されると、理論は振動を受けなければならないと述べている。
基底から励起電子状態への垂直遷移を、空間の所与の領域における核を見つける確率分布を与える振動波動関数から生じるものとして描くと、基底と励起状態における振動波動関数の重なりを与えるオーバーラップ積分\(S_{v’,v}\)から与えられた振動準位の確率を決定することができる。 \(V’\)量子数は基底状態を表し、\(v\)量子数は励起状態を表します。 遷移確率はCondon近似を用いて電子部分と核部分に分けることができる。
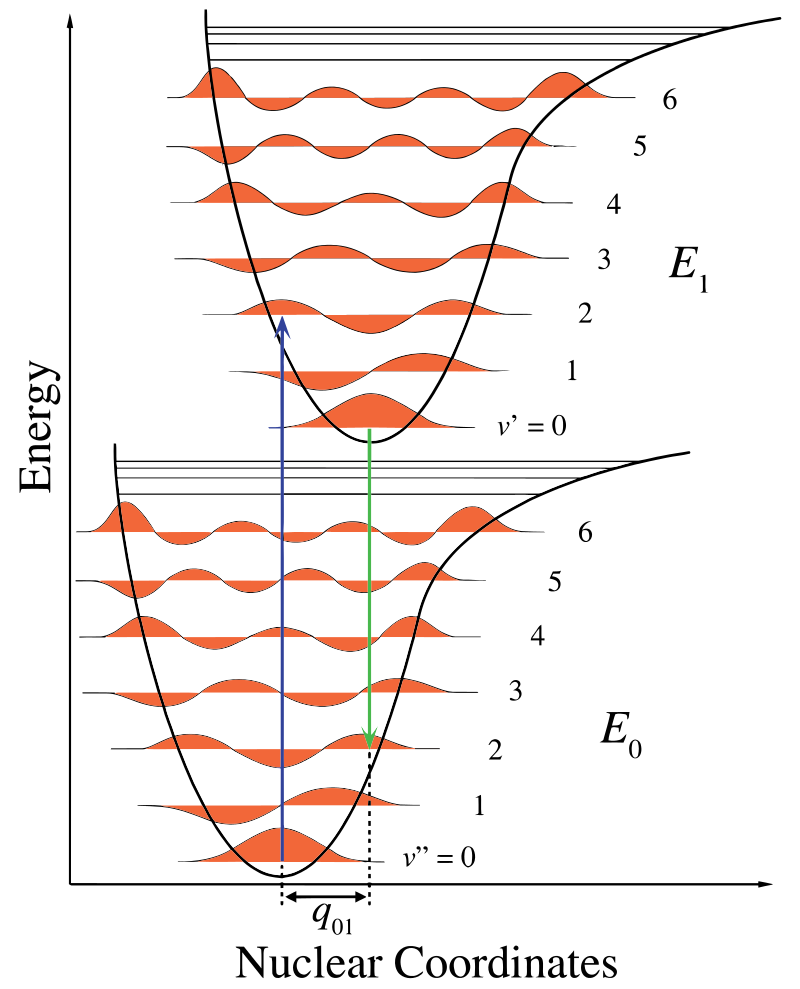
図\(\PageIndex{1}\)では、核軸は核間分離の結果を示し、振動遷移は青と緑の垂直矢印で示されています。 この図は三つのことを示しています:
- 吸収はより高いエネルギー状態につながり、
- 蛍光はより低いエネルギー状態につながり、
- 基底状態と励起状態の間の核座標のシフトは、核相互作用ポテンシャルの新しい平衡位置を示している。 蛍光矢印が吸収よりも短いという事実は、それがより少ないエネルギーを有すること、またはその波長がより長いことを示す。
古典的なコンドン近似
コンドン近似は、電子遷移が核運動に比べて短い時間スケールで発生し、遷移確率が固定された核位置で計算できるという仮定である。
この振動の変化は、急速な電子励起と呼ばれる状態の間に維持される。 結果として得られるクーロン力は、ターニングポイントと呼ばれる核の図に示すように平衡を生成する。 ターニングポイントは、下の曲線の最小値から上の電子状態の交点まで垂直線を描くことによってマッピングすることができます。 この手順は垂直遷移と呼ばれ、以前は光電子分光法(別の電子分光法)の文脈で議論されていました。.
フランク-コンドンの原理は、振動遷移の確率を振動波動関数の重複に関連付けることによって、振動遷移の相対強度を説明します。 振動遷移が起こる確率は、フランク-コンドン重複積分によって重み付けされていると述べています。
\
フランク-コンドン近似内では、核は電子遷移中に”固定”とみなされます。 したがって、電子遷移は、電子ポテンシャルエネルギー曲線上の垂直遷移(図\(\PageIndex{1}\)のvierical遷移)と考えることができる。
量子フランク-コンドンの原理
フランク-コンドンの原理は、古典的なアプリケーションと量子アプリケーションの両方を持っています。 古典的には、Franck–Condonの原理は、分子実体とその環境における核の位置の変化なしに電子遷移が最も起こりやすいという近似である。 結果として得られる状態はFranck–Condon状態と呼ばれ、遷移が関与する垂直遷移と呼ばれます。 この原理の量子力学的定式化は,振動遷移の強度が遷移に関与する二つの状態の振動波動関数間の重複積分の二乗に比例することである。Franc\(q\)とnuclear\(Q\)とnuclear\(q\)とnuclear\(q\)とnuclear\(q\)とnuclear\(Q\)とnuclear\(Q\)とnuclear\(Q\)とnuclear\(Q\)とnuclear\(Q\)とnuclear\(Q\)と.\(Q\)と.\(Q\)と.\(Q\)と.\(Q\)と.\(Q遷移演算子\(\hat{\mu}(q)\)は電子部品のみに依存しているので、核成分は遷移が起こる確率を決定する遷移モーメント積分から分離することができます。\(\hat{\mu}(q)\)は電子部品のみに依存しているので、核成分は遷移が起こる確率を決定する遷移モーメント積分から分離することができます。\(\hat{\mu}(q)\)は電子部品のみに依存しているので、核成分は遷移が起こる確率を決定する遷移モーメント積分から分離することができます。\(\hat{\mu}(q)\)は電子部品のみに依存している。:\langle\psi^{*}_{nuc,f}|\psi_{nuc,i}\rangle}_{\text{核重複}}\langle\psi^{*}_{el,f}|{\boldsymbol{\mu}}|\psi_{el,i}\rangle\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\langle\psi^{*}_{nuc,f}\この遷移の核重畳積分がゼロの場合、電子因子の大きさに関係なく、遷移は観察されません。\rangle\end{align}\]
この遷移の核重畳積分がゼロの場合、電子因子の大きさに関係なく、遷移は観察されません。
\(S_{00}\)高調波発振器モデル内で評価された遷移
ゼロ-ゼロ遷移\(S_{00}\)の核重複は、高調波発振器波動関数のガウス形式の定義を使用して非常に簡ここで、
- \(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、ground alpha=\dfrac{\sqrt{mk}}{\hbar}\(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、excited alpha=\dfrac{\sqrt{mk}}{\hbar}\(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、excited alpha=\dfrac{\sqrt{mk}}{\hbar}\(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、excited alpha=\dfrac{\sqrt{mk}}{\hbar}\(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、excited alpha=\dfrac{\sqrt{mk}}{\hbar}\(\alpha=\dfrac{\sqrt{mk}}{\hbar}\)は、excited alpha=\dfrac{\sqrt{mk}}{\hbar}\(p>核重複積分は
\
式\(\ref{fc1}\)の指数は次のように展開できます
\
式\(\ref{fc1}\)の指数は次のように展開できます
\
式\(\ref{fc1}\)の指数は次のように展開できます
\
式\(\ref{fc1}\)の指数は次のように展開できます
\
\
そして、私たちは使用します
\
そして、
\
積分内の正方形を代入して完成させます。 私たちは表現することができます
\。したがって、式\(\ref{FC2}\)の積分は
\
積分はガウス積分です。 この積分は、積分の表からすでに解かれています。\(\ref{FC3}\)は
\
この積分は、積分の表から、方程式\(\ref{FC3}\)になります
\
この積分はすでに解かれています
\
この積分はすでに解かれています
\
この積分はすでに解かれています
\
この積分はすでに解かれています私たちは、励起状態の最初の励起振動レベルに地面にゼロレベルの振動の重なりを計算するために、同じ手順に従います:\(s_{01}\)。
\(S_{01}\)調和振動子モデル内で評価された遷移
ゼロの基底状態レベル(\(v=0\))と最初の励起状態レベル(\(v’=1\))の重なりを計算するために、励起状態波動関数を記述するためにエルミート多項式\(H_1(x)=2x\)を使用します(調和振動子波動関数のレビューについてはこちらを参照してください)。 ここで、\(x=\sqrt{\alpha}(R-Q_E)\)です。
\
基底電子状態のゼロ点波動関数は
\
励起電子状態の最初の励起状態波動関数は
\
ゼロ点波動関数のオーバーラップは
\
最初の励起状態レベル(式\(\ref{fc01}\))を持つ基底状態レベルは、
\
と
\
積分が次のように書くことができるように、上記と同じ置換を行うことができます(図示せず、宿題の演習で実証される)。 最後の結果は
\
基底状態のゼロレベルとすべてのより高い光振動レベルとの重複を続けて計算することができます:\(S_{02}\)、\(S_{03}\)など。 振動準位は異なるエネルギーを有するので、各項は異なるエネルギーを有する遷移に対応する。 吸収バンドは、それ自身の確率でそれぞれ異なるレベル間の遷移の進行(Franck-Condon進行)の外観を有する。FC因子に対する上記の式の重要性を理解するために、\(T=0\)ケルビンでの基底と励起状態のポテンシャルエネルギー表面を調べてみましょう。 以下に示すのは、エネルギーが8,000cm-1で区切られた二つの状態である。 これは、それらの潜在的な井戸の底部間のエネルギー分離であるが、それぞれのゼロ点エネルギーレベル間のエネルギー分離でもある。 振動モードのumberが1,000cm-1であり、電子が結合軌道から除去され、電子励起時に反結合軌道に置かれるという事実によって結合長が増加すると仮定し
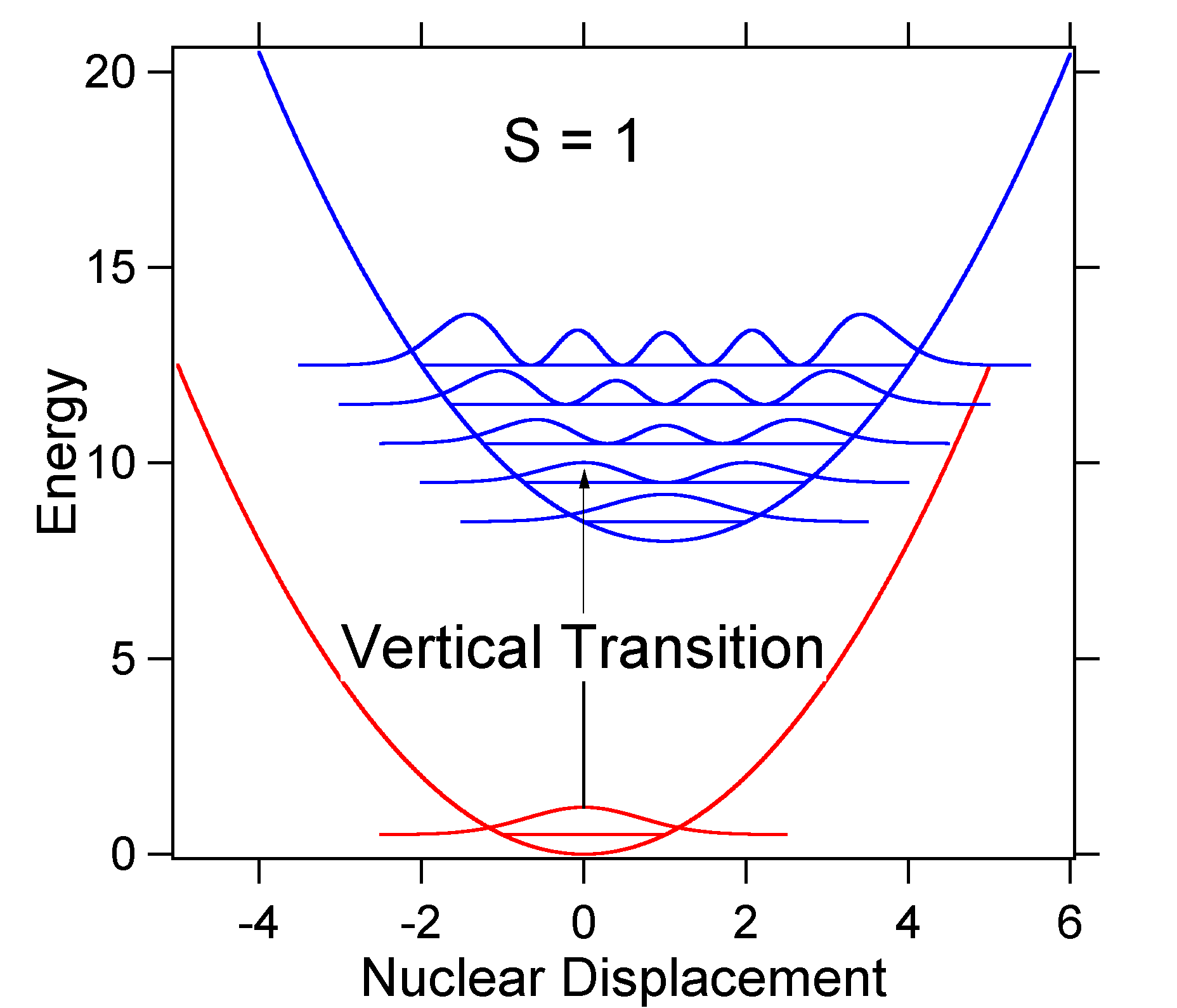
フランク-コンドン因子の上記のモデルによれば、我々は”スティック”スペクトルを生成します(図\(\PageIndex{3}\))各振動遷移は無限に狭く、遷移は\(e=h\nu\)正確に 例えば、ポテンシャルエネルギー面はS=1に対して与えられ、各レベルでの遷移確率は下の図の棒(黒)によって与えられる。p>
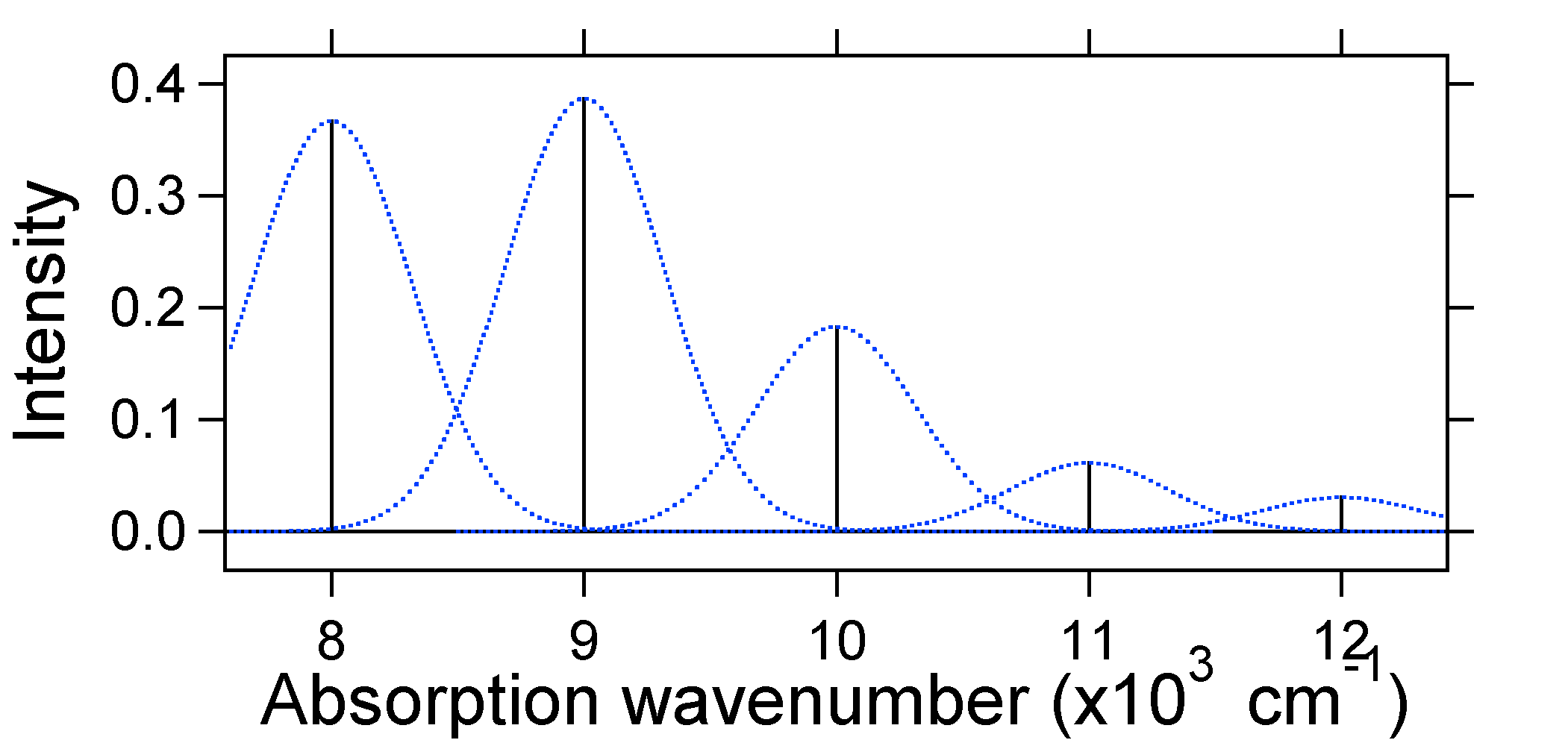
各スティックを囲む点線のガウスは、吸収スペクトルがどのように見えるべきかのより現実的な画像を与えます。 この最初の場所では、各エネルギー準位(スティック)は、状態が有限の寿命を有するという事実によってある程度の幅が与えられる。 このような広がりは、アンサンブル内のすべての分子に同様の方法で影響を与えるため、均質広がりと呼ばれます。 また、各分子の環境に小さな違いがあるために広がっています。 このタイプの広がりは、不均一な広がりと呼ばれます。 起源にかかわらず、上記のモデルはガウス広がりを用いて作成された
基底状態と励起状態の間の核変位は、吸収スペクトルの形状を決定する。 より小さい励起状態変位と大きな励起状態変位の両方を調べてみましょう。 この場合のポテンシャルエネルギー面は次のとおりです。
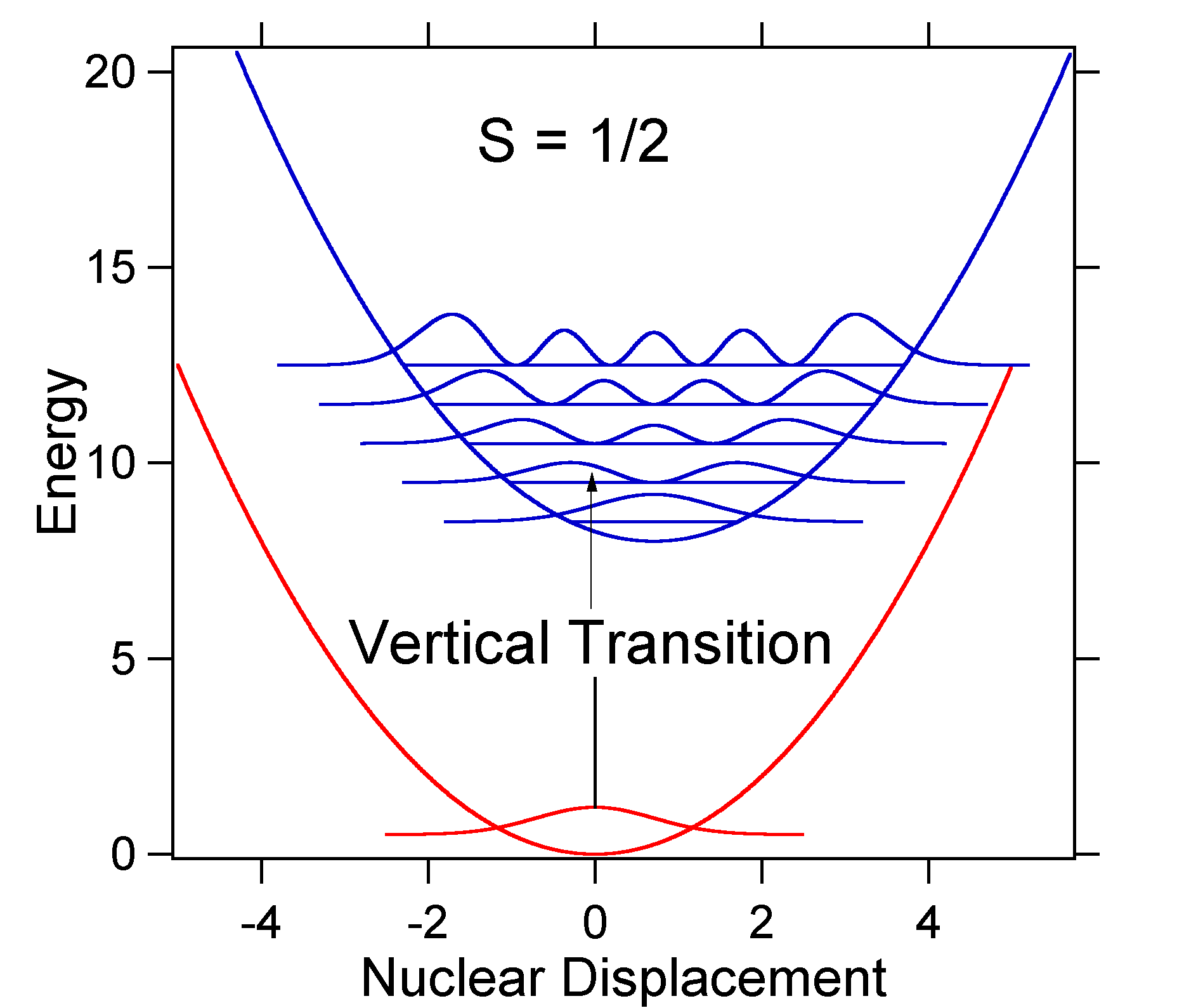
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
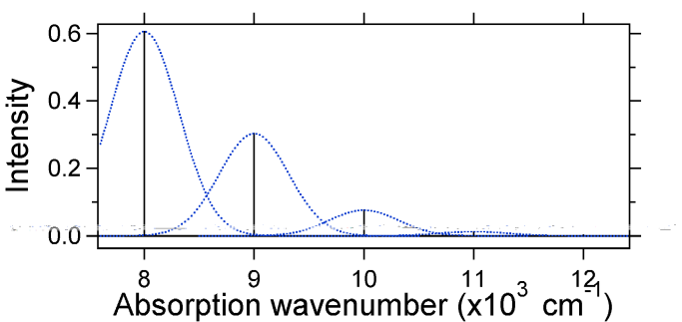
変位が小さい場合、ゼロ-ゼロまたは\(S_{0,0}\)振動遷移は非常に大きいことに注意してください。一般的な経験則として、\(S\)定数は、\(v=2\)遷移の強度と\(v=1\)遷移の強度の比を与えます。\(v=1\)遷移の強度は、\(V=2\)遷移の強度の比を与えます。\(v=1\)遷移の強度の比を与えます。\(V=2\)遷移の強度の比を与えます。 この場合、\(S=0.5\)なので、\(v=2\)遷移は\(v=1\)遷移の強度0.5になります。より大きな変位の例として、S=2のポテンシャルエネルギー面の配置を以下に示します。
より大きな変位の例として、s=2のポテンシャルエネルギー面の配置を以下に示します。
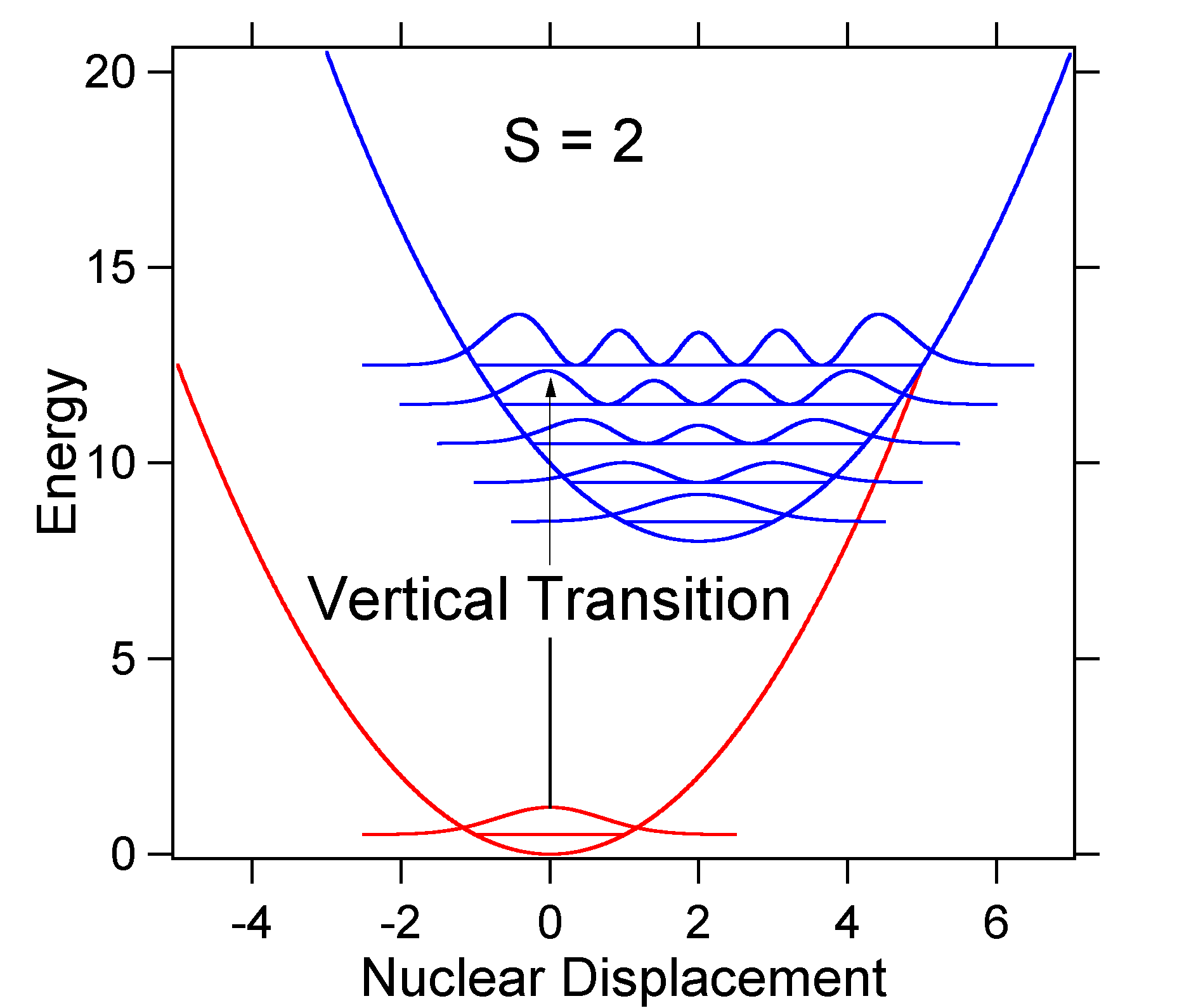
変位が大きいほど、基底状態レベルと励起状態のv=0レベルとの重複が減少します。 最大強度は、スティックスペクトルに示されているように、より高い振動レベルで達成されます。p>
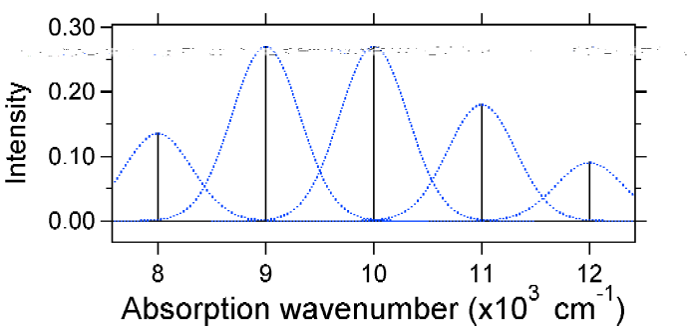
下にプロットされた吸収スペクトルはすべて同じ積分強度を持っていますが、励起状態ポテンシャルエネルギー表面の変位の程度が異
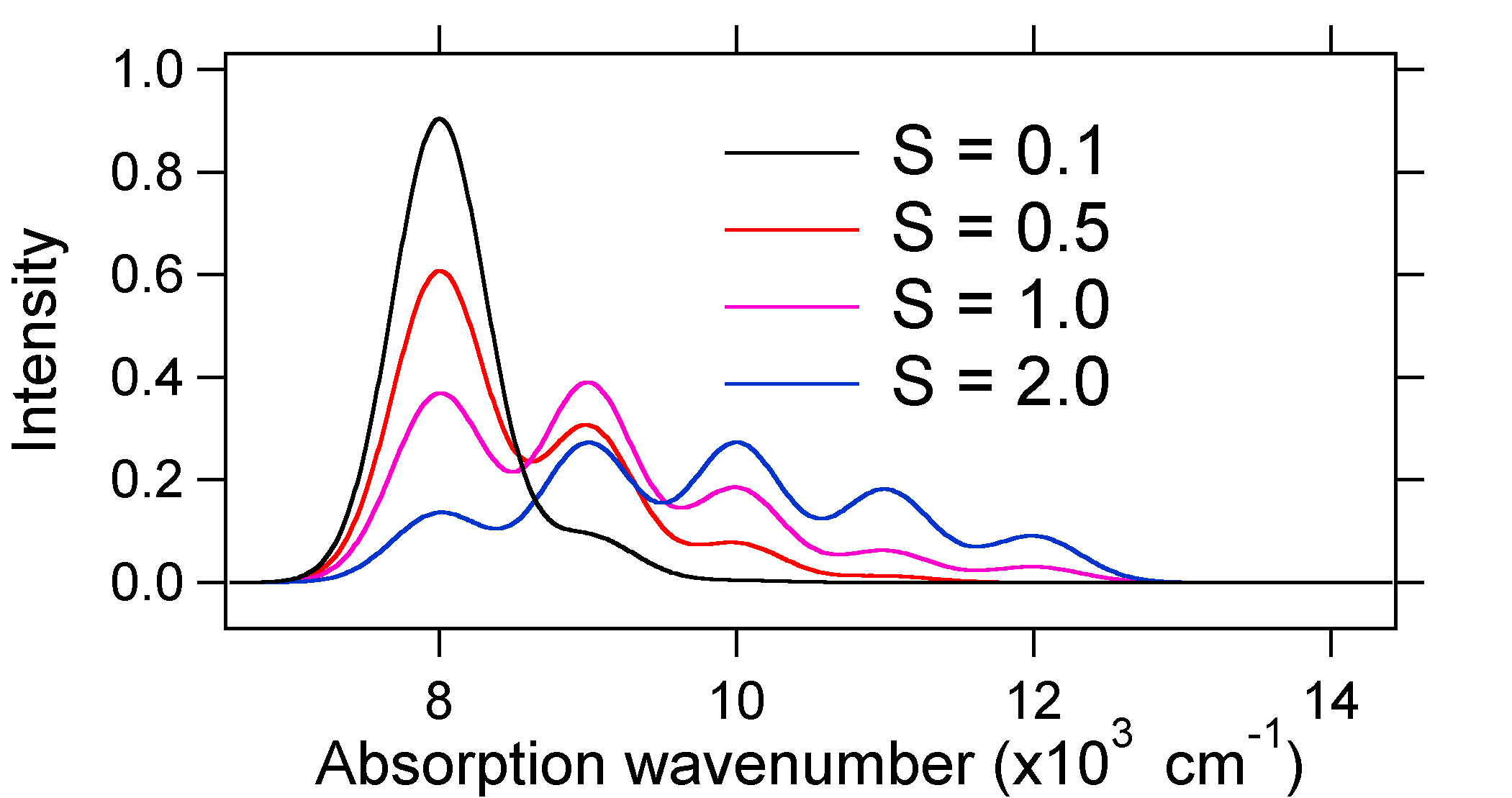
だから、相対的な振動バンド強度の性質は、遷移を伴う平衡核座標の変位があるかどうかを伝えることができます。 結合長が増加するのはいつですか(つまり、\(Q_E>R_E\))? これは、電子が結合分子軌道から非結合または反結合分子軌道に促進されるときに起こる(すなわち、結合秩序が基底状態よりも励起状態にないとき)。
- 非結合分子軌道\(\rightarrow\)結合分子軌道
- 反結合分子軌道\(\rightarrow\)結合分子軌道
- 反結合分子軌道\(\rightarrow\)非結合分子軌道
要するに、結合順序が基底状態よりも励起状態で低い場合、\(Q_E>r_e\);これが発生すると、bondlengthの増加が発生します。
- J.M.Luis、D.M.Bishop、B.Kirtman。 非調和性を含むFranck–Condon因子を計算するための別のアプローチ。 J.Chem. フィス 120(2004),pp.813-822.
- アトキンス、ピーターとフリオ*デ*ポーラ。 生命科学のための物理化学。 2006. ニューヨーク、ニューヨーク:W.H.フリーマンと会社。 p.563-564
- フランク-コンドンの原則。 1996, 68, 2243. IUPAC Compendium Of Chemical Terminology第2版(1997年)。 www.iupac.org/goldbook/F02510.pdf
- E.RabinowitchとGovindjee。 光の吸収とエネルギーの励起の運命。 1969. フランク=コンドンの原理。 http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
貢献者
- Matthe Zi Ziering
-
Stefan Franzen(North Carolina State University)
貢献者
- Matthe Zi Ziering(North Carolina State University)
貢献者
- Matthe Zi Ziering(North Carolina State University)