Het Franck-Condon-principe beschrijft de intensiteit van vibronische overgangen, of de absorptie of emissie van een foton. Het stelt dat wanneer een molecuul een elektronische overgang, zoals ionisatie ondergaat, de nucleaire configuratie van de molecule geen significante verandering ervaart. Dit komt in feite doordat kernen veel massiever zijn dan elektronen en de elektronische overgang sneller plaatsvindt dan de kernen kunnen reageren. Wanneer de kern zich aanpast aan de nieuwe elektronische configuratie, stelt de theorie dat hij een trilling moet ondergaan.
als we ons de verticale overgang van de grond naar de opgewekte elektronische toestand voorstellen als die plaatsvindt vanuit een trillingsgolffunctie die een kansverdeling geeft van het vinden van de kernen in een gegeven ruimtegebied,kunnen we de waarschijnlijkheid van een gegeven trillingsniveau bepalen vanuit de overlapintegraal \(S_{v’, v}\) die de overlap geeft van de trillingsgolffunctie in de grond en de opgewekte toestand. De\ (v’\) kwantumgetallen verwijzen naar de grondtoestand en de\ (v\) kwantumgetallen verwijzen naar de opgewekte toestand. De kans op overgang kan worden gescheiden in elektronische en nucleaire delen met behulp van de Condon benadering.
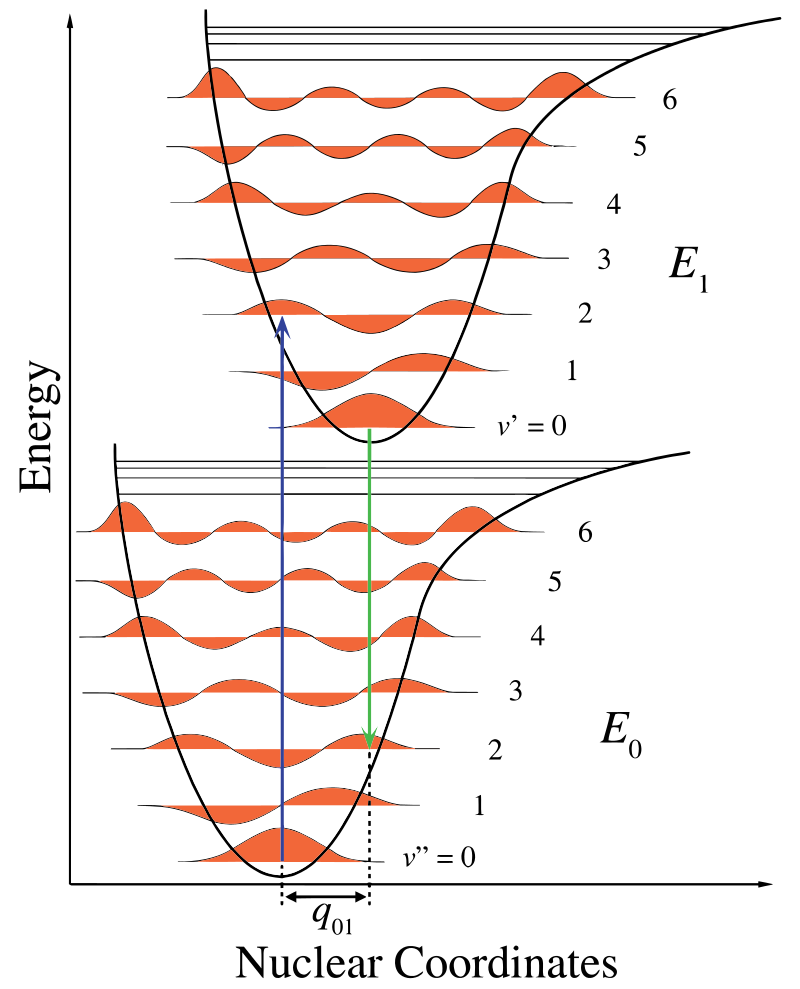
in Figuur \(\Paginindex{1}\) toont de kernas een gevolg van de internucleaire scheiding en wordt de vibronische overgang aangegeven door de blauwe en groene verticale pijlen. Dit cijfer toont drie dingen:
- een absorptie leidt tot een hogere energietoestand,
- fluorescentie leidt tot een lagere energietoestand, en
- de verschuiving in nucleaire coördinaten tussen de grondtoestand en de opgewekte toestand wijst op een nieuwe evenwichtspositie voor het kerninteractiepotentieel. Het feit dat de fluorescentiepijl korter is dan de absorptie wijst erop dat het minder energie heeft, of dat zijn golflengte langer is.
de klassieke condonbenadering
Condonbenadering is de aanname dat de elektronische overgang plaatsvindt op een korte tijdschaal in vergelijking met nucleaire beweging, zodat de kans op overgang op een vaste nucleaire positie kan worden berekend.
Deze verandering in trilling wordt gehandhaafd tijdens een toestand die de snelle elektronische excitatie wordt genoemd. De resulterende Coulombische krachten produceren een evenwicht zoals getoond in de figuur voor de kernen genoemd een keerpunt. Het keerpunt kan in kaart worden gebracht door een verticale lijn te trekken van het minimum van de lagere kromme tot het snijpunt van de hogere elektronische toestand. Deze procedure wordt genoemd een verticale overgang en werd eerder besproken in de context van Photo-elektron spectroscopie (een andere elektronische spectroscoy)..
Het Franck-Condon-Principe verklaart de relatieve intensiteit van vibronovergangen door de waarschijnlijkheid van een trillingsovergang te relateren aan de overlapping van de trillingsgolffuncties. Het stelt dat de kans op een trillingsovergang wordt gewogen door de Franck-Condon-overlappingsintegraal:
\
binnen de Franck-Condon-benadering worden de kernen tijdens elektronische overgangen als “vast” beschouwd. Elektronische overgangen kunnen dus worden beschouwd als verticale overgangen op elektronische potentiaalenergiekrommen (vierische overgangen in Figuur \(\Paginindex{1}\)).
Het Quantum Franck-Condon Principe
Het Franck-Condon principe heeft zowel een klassieke als een Kwantumtoepassing. Klassiek is het Franck-Condon principe de benadering dat een elektronische overgang het meest waarschijnlijk zal plaatsvinden zonder veranderingen in de posities van de kernen in de moleculaire entiteit en haar omgeving. De resulterende staat heet een Franck-Condon staat, en de overgang betrokken, een verticale overgang. De kwantummechanische formulering van dit principe is dat de intensiteit van een vibronische overgang evenredig is met het kwadraat van de overlappingsintegraal tussen de trillingsgolffuncties van de twee toestanden die betrokken zijn bij de overgang.
Het Franck-Condon principe is gebaseerd op de born-Oppenheimer benadering, die scheiding mogelijk maakt van de elektronische \(q\) en nucleaire \(Q\) golffunctie gegeven de totale golffunctie.
\
aangezien de transitie-operator, \(\hat{\mu}(q)\), alleen afhankelijk is van de elektronische component, kunnen de nucleaire componenten worden gescheiden van de transitiemoment-integraal die de waarschijnlijkheid van de transitie bepaalt:
&= \underbrace{ \langle \psi^{*}_{noc, f} | \psi_{noc, i} \rangle}_{\text{nucleaire overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, ik} \rangle \end{align}\]
Als de nucleaire overlap integraal is nul voor deze overgang, dan is de overgang zal niet in acht worden genomen, ongeacht de omvang van de elektronische factor.
\(s_{00}\) overgang geëvalueerd binnen harmonische Oscillator model
de nucleaire overlap voor de nul-nul overgang \(S_{00}\) kan eenvoudig worden berekend met behulp van de definitie van de Gaussiaanse vorm van de harmonische oscillator golffuncties.
Het nul-punt wavefunction in de grond elektronische toestand is
\
Het nul-punt wavefunction in de opgewonden elektronische toestand is
\
waar
- \(\alpha = \dfrac{\sqrt{mk}}{\hbar}\)
- \(R_e\) is het evenwicht band lengte in de grond elektronische staat
- \(Q_e\) is het evenwicht band lengte in de opgewonden elektronische staat
De nucleaire overlap integraal
\
De exponent in Vergelijking \(\ref{VV 1}\) kan worden uitgebreid
\
en we gebruiken
\
en
\
om het vierkant binnen de integraal te vervangen en te voltooien. We kunnen
\.\]
De integraal in vergelijking \(\ref{FC2}\) is dus
\
De integraal is een Gaussiaanse integraal. Je kunt laten zien dat als we \(z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}\) dan \(dz = \sqrt{\alpha} dR\) en de integraal wordt
\
deze integraal is al opgelost, uit een tabel met integralen wordt vergelijking \(\ref{FC3}\)
\
We zouden dezelfde procedure volgen om die overlapping van de nulde trilling in de grond te berekenen naar het eerste opgewonden trillingsniveau van de opgewonden toestand: \(s_{01}\).
\(S_{01}\) overgang geëvalueerd binnen harmonische Oscillator model
om de overlap van nulth ground state level (\(v=0\)) te berekenen met het eerste geëxciteerde state level (\(v’ = 1\)) gebruiken we de Hermite polynoom \(H_1 (x) = 2x\) voor het beschrijven van de geëxciteerde state golffunction (zie hier voor een overzicht van harmonische oscillator wavefunctions). Hier \(x = \sqrt{\alpha} (R – Q_e)\).
\
met het nul-punt wavefunction in de grond elektronische toestand is
\
De eerste aangeslagen toestand wavefunction in de opgewonden elektronische toestand is
\
De overlap van nulde grond niveau met de eerste aangeslagen toestand niveau (Vergelijking \(\ref{FC01}\)) is dan
\
en
\
hetzelfde vervangingen kunnen worden gemaakt als boven, zodat de integraal kan worden geschreven als (niet weergegeven en aangetoond te worden in een huiswerk-oefeningen) en het eindresultaat is
\
We kunnen doorgaan en berekenen dat het Nulde niveau in de grondtoestand overlapt met alle hogere licht trillingsniveaus: \(s_{02}\), \(S_{03}\), enz. Elke term komt overeen met een overgang met een andere energie omdat de trillingsniveaus verschillende energieën hebben. De absorptieband heeft dan het uiterlijk van een progressie (een Franck-Condon progressie) van overgangen tussen verschillende niveaus elk met zijn eigen waarschijnlijkheid.
Franck-Condon progressies
om de Betekenis van de bovenstaande formule voor de FC-factor te begrijpen, laten we een aardoppervlak en een opgewekte toestand van potentiële energie-oppervlak op \(T = 0\) Kelvin onderzoeken. Hieronder zijn twee toestanden gescheiden door 8.000 cm-1 in energie. Dit is energiescheiding tussen de bodems van hun potentiële putten, maar ook tussen de respectieve nulpuntsenergieniveaus. Laten we aannemen dat het wavengetal van de trillingsmodus 1.000 cm-1 is en dat de bindingslengte wordt verhoogd omdat een elektron uit een bindingsbaan wordt verwijderd en in een anti-bindingsbaan wordt geplaatst bij elektronische excitatie.
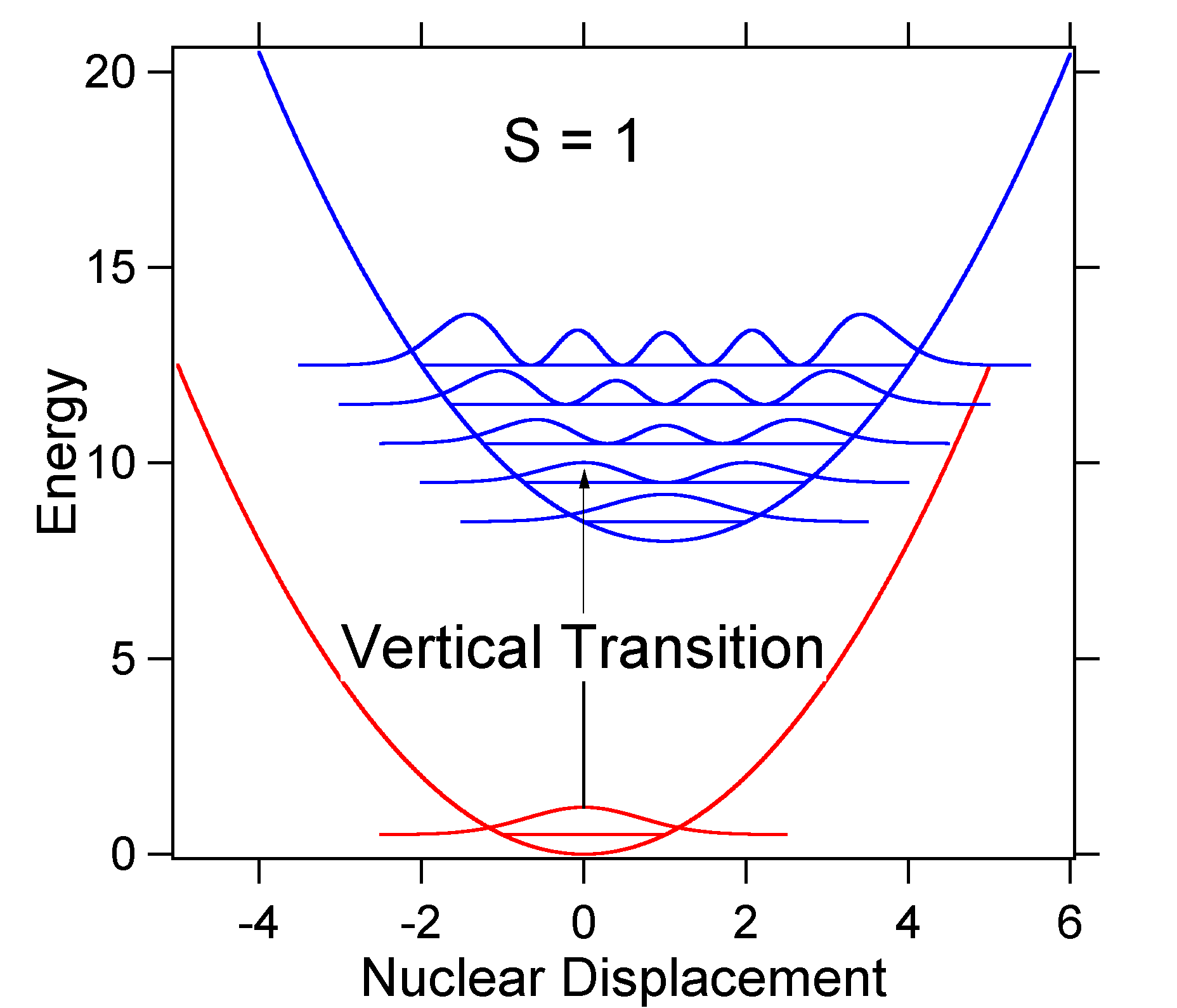
volgens het bovenstaande model voor de Franck-Condon factor zouden we een” stick ” spectrum genereren (figuur \(\Paginindex{3}\)) waarbij elke trillingsovergang oneindig smal is en overgang alleen kan plaatsvinden wanneer \(E = H\nu\) precies. Bijvoorbeeld, de potentiële energieoppervlakken werden gegeven voor S = 1 en de overgangswaarschijnlijkheid op elk niveau wordt gegeven door de stokken (zwart) in de onderstaande figuur.
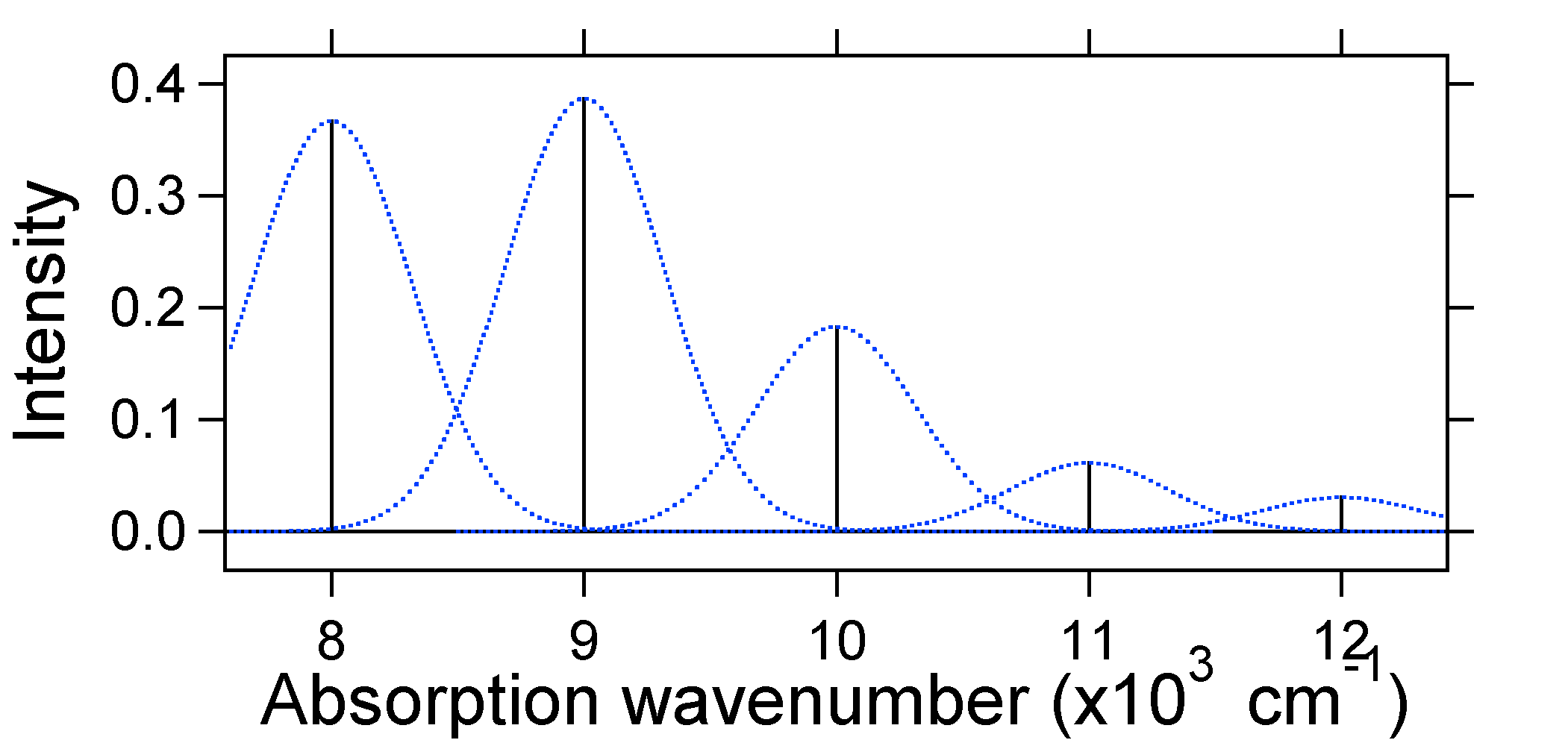
de gestippelde Gaussianen rond elke stick geven een realistischer beeld van hoe het absorptiespectrum eruit moet zien. In deze eerste plaats zal elk energieniveau (stok) enige breedte gegeven worden door het feit dat de toestand een eindige levensduur heeft. Een dergelijke verbreding wordt homogene verbreding genoemd omdat het alle moleculen in het ensemble op een vergelijkbare manier beïnvloedt. Er is ook verbreding toe te schrijven aan kleine verschillen in het milieu van elke molecule. Dit type verbreding wordt inhomogene verbreding genoemd. Ongeacht de oorsprong van het bovenstaande model is gemaakt met behulp van een Gaussiaanse verbreding
de nucleaire verplaatsing tussen de grond en de opgewekte toestand bepaalt de vorm van het absorptiespectrum. Laten we zowel een kleinere als een grote opgewekte toestand verplaatsing onderzoeken. Als \(S=½\) en de potentiële energieoppervlakken in dit geval:
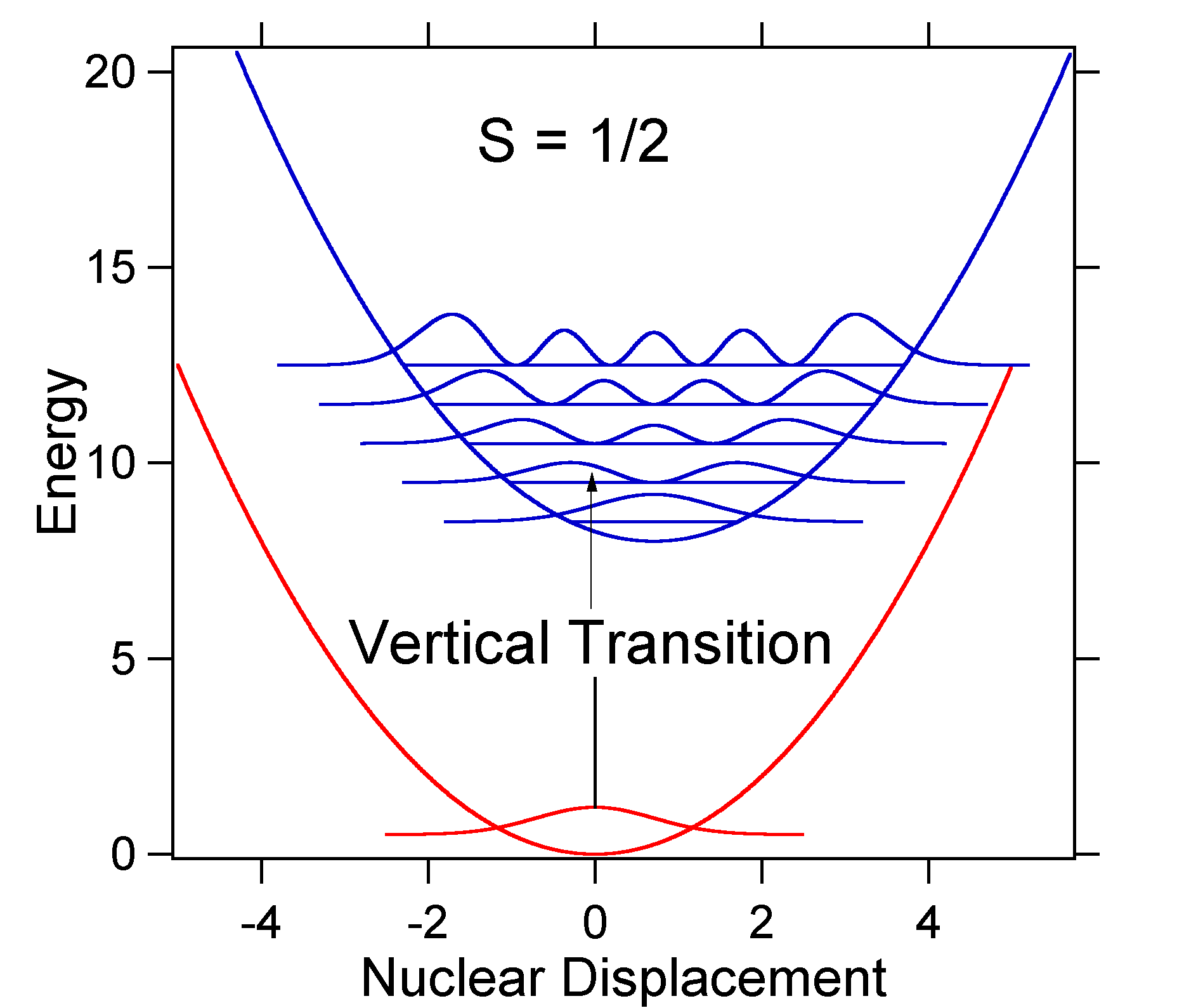
For this case the “stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
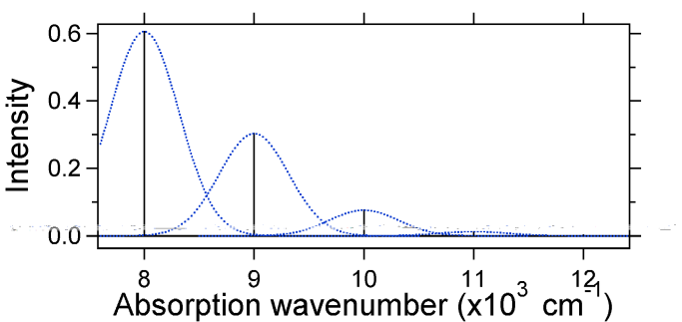
merk op dat de nul-nul of \(s_{0,0}\) trillingsovergang veel groot is in het geval dat de verplaatsing klein is.
als algemene vuistregel geeft de \(S\) constante de verhouding van de intensiteit van de \(v = 2\) overgang naar de \ (v = 1\) overgang. In dit geval is de \(v = 2\) overgang sinds \(S=0.5\) 0,5 de intensiteit van \(v=1\) overgang.
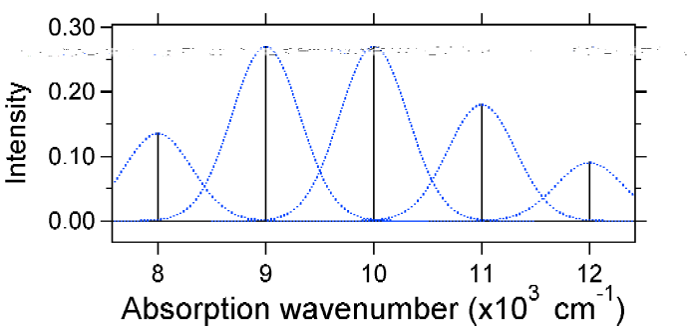
als voorbeeld van een grotere verplaatsing wordt de dispositie van de potentiële energieoppervlakken voor S = 2 hieronder weergegeven.
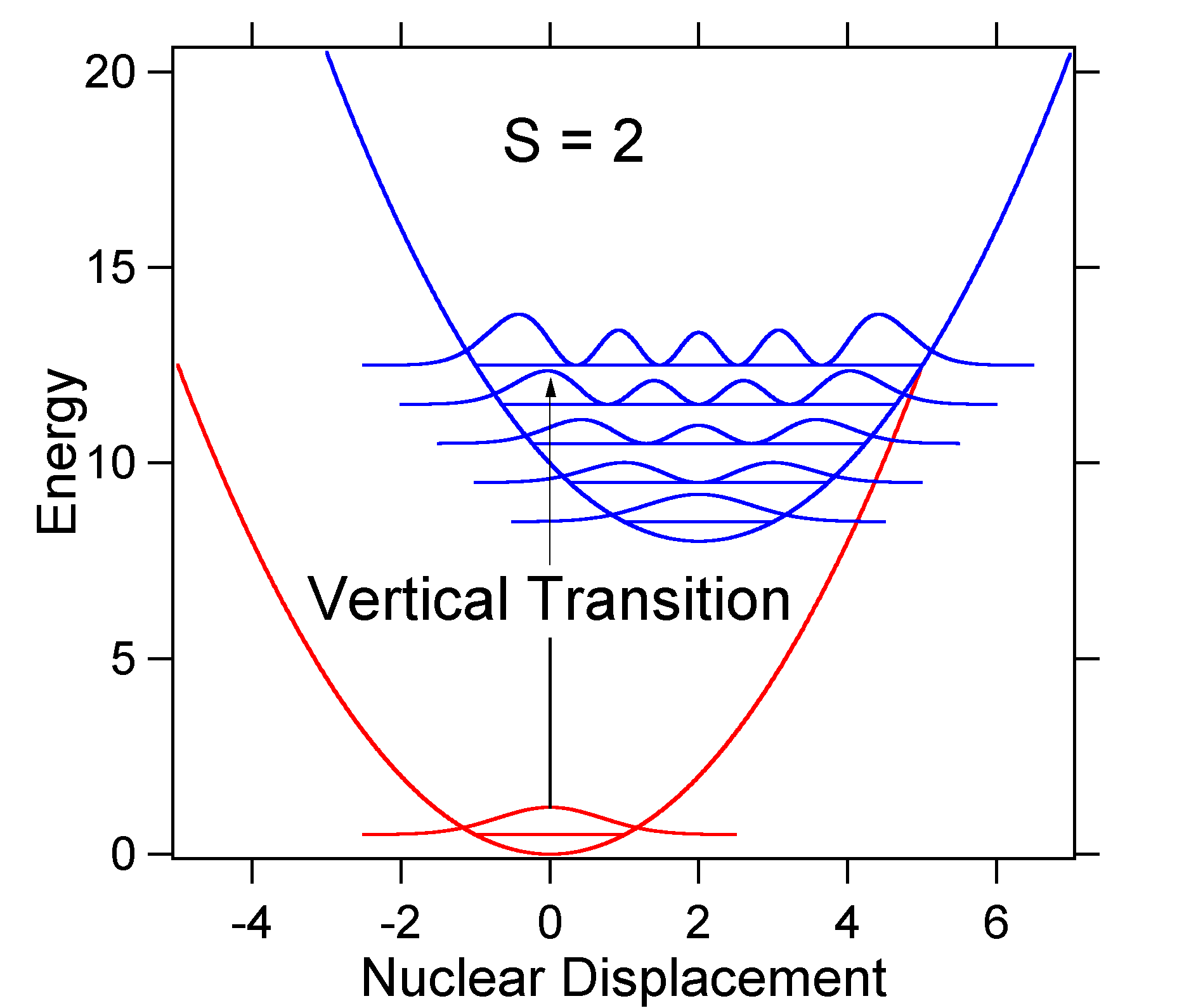
de grotere verplaatsing resulteert in een verminderde overlap van het niveau van de grondtoestand met het niveau v = 0 van de opgewekte toestand. De maximale intensiteit zal worden bereikt in hogere trillingsniveaus zoals aangegeven in het stokspectrum.
de hieronder afgebeelde absorptiespectra hebben allemaal dezelfde geïntegreerde intensiteit, maar hun vorm wordt gewijzigd door de verschillende mate van verplaatsing van het potentiële energieoppervlak van de opgewekte toestand.
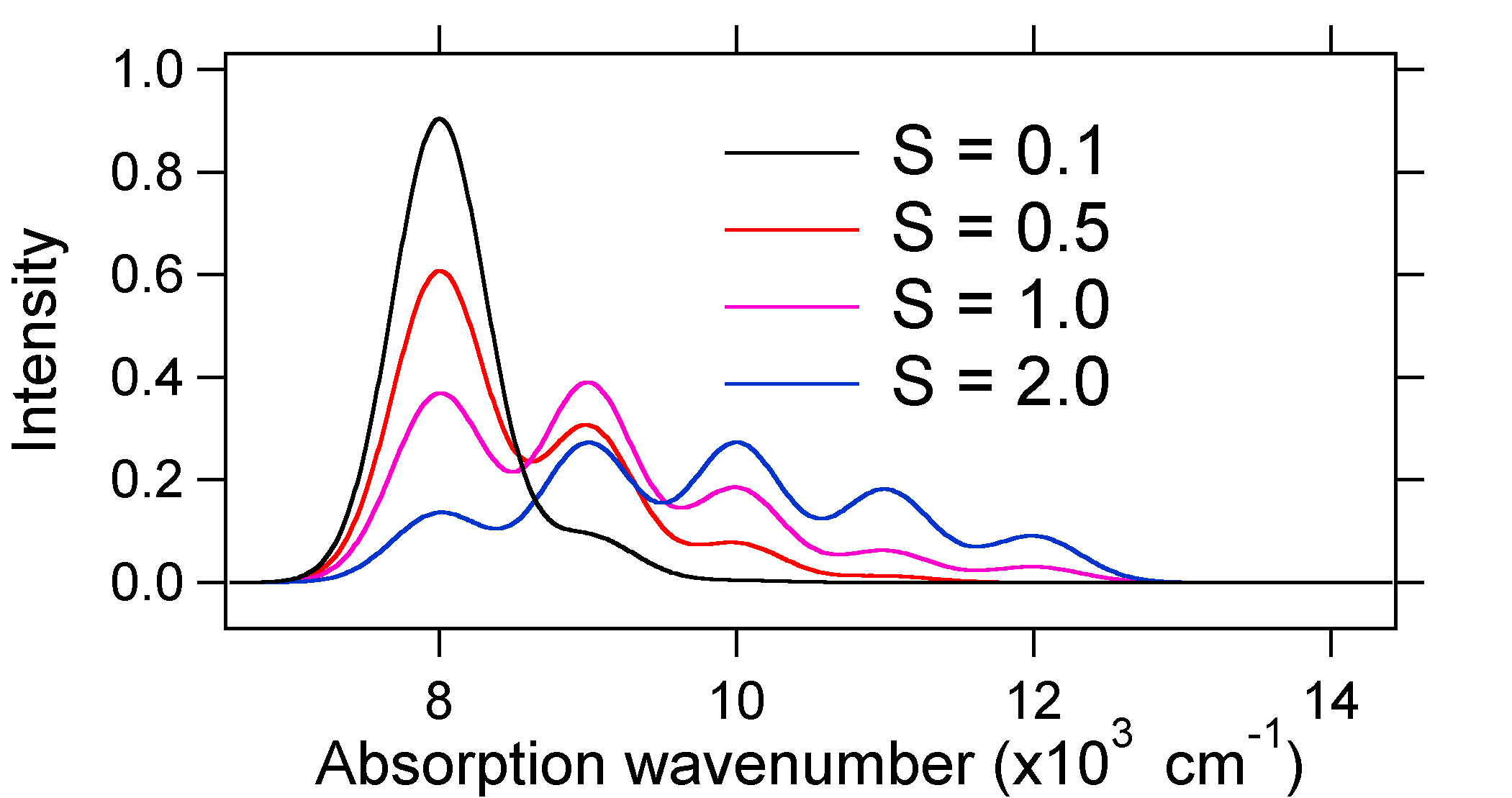
dus de aard van de relatieve vibronische bandintensiteit kan ons vertellen of er een verplaatsing van de evenwichtskerncoördinaat is die een overgang vergezelde. Wanneer zal er een toename in obligatielengte zijn (d.w.z. \(Q_e > R_e\))? Dit gebeurt wanneer een elektron wordt bevorderd van een binding moleculaire orbitaal naar een niet-Binding of anti-binding moleculaire orbitalen (dat wil zeggen, wanneer de binding orde is minder in de opgewonden toestand dan de grond toestand).
- Non-bonding moleculaire orbitaal \(\rightarrow\) lijmen moleculaire orbitaal
- Anti-bonding moleculaire orbitaal \(\rightarrow\) lijmen moleculaire orbitaal
- Anti-bonding moleculaire orbitaal \(\rightarrow\) non-bonding moleculaire orbitaal
In het kort, wanneer de bond om lager in de aangeslagen toestand dan in de grond staat, dan \(Q_e > R_e\); een toename in bondlength zal optreden wanneer dit gebeurt.
- J. M. Luis, D. M. Bishop, B. Kirtman. Een andere benadering voor het berekenen van Franck-Condon factoren, waaronder anharmoniciteit. J. Chem. Phys., 120 (2004), pp.813-822.Atkins, Peter en Julio De Paula. Fysische chemie voor de biowetenschappen. 2006. New York, NY: W. H. Freeman and Company. P. 563-564
- Franck-Condon Principle. 1996, 68, 2243. IUPAC Compendium of Chemical Terminology 2nd Edition (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowitch and Govindjee. Lichtabsorptie en het lot van opwinding van energie. 1969. Franck-Condon Principe. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
bijdragers
- Matthe Zi Ziering
-
Stefan Franzen (North Carolina State University)