de wiskunde van landmeetkunde: Deel II. de Planimeter

geplaatst in juni 2008.

de tweede van twee kolommen over de wiskunde van landmeetkunde (de eerste is hier). …

Bill Casselman
Universiteit van British Columbia, Vancouver, Canada
cass at math.ubc.ca

John Eggers
University of California, San Diego
jeggers at ucsd.edu

e-Mail naar een vriend

Print dit artikel

Een planimeter is een table-top instrument voor het meten van gebieden, meestal de gebieden van onregelmatige regio ‘ s op een kaart of foto. Ze waren ooit gebruikelijk, maar zijn nu grotendeels vervangen door digitale tools.

de volgende afbeelding geeft een idee van de instelling. De poolarm draait vrij rond de paal, die op de tafel is bevestigd. De tracer arm draait rond de pivot, dat is waar het zich aansluit bij de polaire arm. Je volgt met de tracer een curve in de richting van de klok mee, en terwijl je dat doet rolt het meetwiel mee, en de totale afstand die het rolt wordt verzameld op de wijzerplaat. Het steunwiel zorgt ervoor dat het ding niet omvalt. Aan het einde lees je een getal af van de wijzerplaat, en na vermenigvuldiging met een factor die alleen afhankelijk is van de specifieke configuratie van de planimeter, krijg je het gebied binnen de curve.

de volgende figuur geeft een beter beeld van het mechanisme.

we noemen de drager de assemblage van wielen, draaiknop en draaiknop. In de volgende foto krijg je een betere blik op het, en kan de worm rijden die ervoor zorgt dat de wijzerplaat te draaien als het meetwiel beweegt zien.

Hier is het diagram van de oorspronkelijke planimeter, uit het artikel van Jakob Amsler dat het introduceerde:

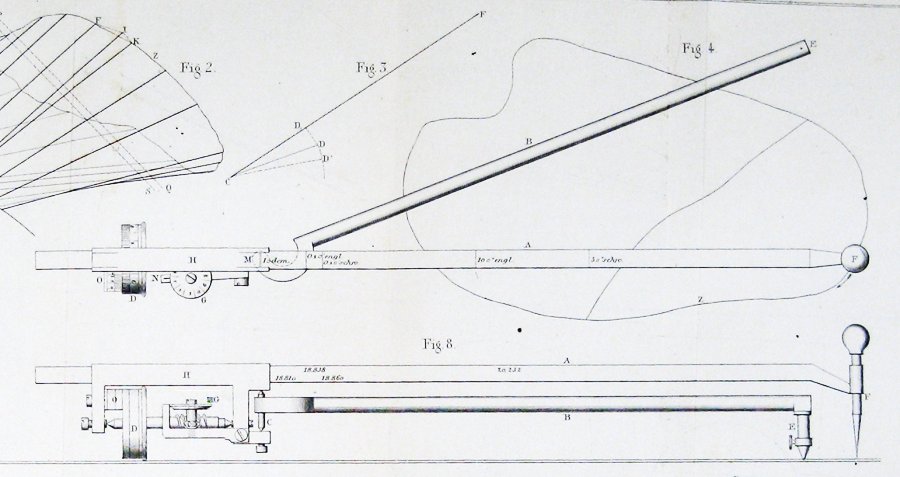
Hoe kan zo ‘ n eenvoudig ding gebieden meten?

meetkunde van de planimeter

De beweging met de klok mee van de planimeter is de richting die tegengesteld is aan wat wiskundigen hebben besloten positieve rotatie te zijn. In plaats van deze conventie te schenden, gaan we vanaf nu werken met de planimeter van een wiskundige, waarin je tegen de klok in beweegt. Net als andere wiskundigen fantasieën, er zijn geen op de planeet!

Er zijn enkele beperkingen voor het plaatsen van de planimeter ten opzichte van de curve die u wilt traceren. De drager kan langs de tracerarm worden geschoven, maar in alle gevallen is de lengte l van de tracerarm kleiner dan de lengte r van de poolarm. Dit betekent dat de tracer nooit binnen een afstand r – l van de paal kan komen. Aan de andere kant, wanneer het volledig uitgeschoven is, kan de tracer nooit verder reiken dan r + l. dus moet de te traceren kromme binnen de annulus liggen tussen twee cirkels, één met straal r – l, de andere r + l.

in feite zou het in een moment duidelijk moeten worden dat de armen nooit volledig uitgeschoven mogen worden, zodat de curve die moet worden getraceerd volledig in de annulus moet liggen. Bovendien wordt de paal normaal gesproken aan de buitenkant van de bocht geplaatst.

voor een bepaald punt in de annulus zijn er precies twee mogelijke configuraties van de planimeter die de tracer op dat punt plaatsen. Het kiezen van een punt of het andere betekent het kiezen van een teken voor een vierkantswortel. We noemen dit het kiezen van een oriëntatie voor de planimeter. Het is positief als de vierkantswortel positief is. Zodra een oriëntatie is gekozen, blijft deze hetzelfde, tenzij de arm volledig is uitgeschoven. Dit mag nooit gebeuren. Zolang je curve zich volledig binnen de annulus bevindt, zullen de configuraties van de planimeter soepel en uniek variëren met het pad van de tracer.

het volgende wat je moet doen is een paar dingen begrijpen over de beweging van het meetwiel. Zoals de volgende afbeelding laat zien, draait het wiel in een rechte lijn A afstand C door een hoek θ = C/R waarbij R de straal is.

Het is dus waar dat de rotatie van het wiel en de afstand die de tracer-arm aflegt een relatie met elkaar hebben. Maar deze relatie is een beetje subtiel. Als de arm gewoon recht vooruit een afstand C, het gebied geveegd zal lC, maar als het verschuift evenwijdig aan zichzelf het gebied geveegd zal zijn 0. In het eerste geval zal een punt op de omtrek van het wiel afstand C verplaatsen.in het tweede geval zal het wiel helemaal niet bewegen. En als de arm schuin vertaalt, zal het wiel een afstand draaien die gelijk is aan de hoogte van het parallellogram dat door de arm wordt bedekt. In alle gevallen waarin de arm evenwijdig aan zichzelf vertaalt, is het door het deel van de indicatorgam tussen het draaipunt en de tracer weggevaagd gebied gelijk aan lC, waarbij C de afstand is die door de rotatie van het wiel wordt gemeten. Dit is het basisfeit dat de armbeweging relateert aan de beweging van het meetwiel.

de manier om dit precies uit te drukken is dat ongeacht hoe de arm beweegt, de door het wiel gemeten afstand de integraal van het pad is

waarbij Γ het pad is dat wordt afgelegd door het punt van de arm waar het meetwiel is bevestigd, n de eenheidsvector loodrecht op de arm op elk moment; en T is de eenheidsvector die in de rijrichting wijst (zodat, bijvoorbeeld, als de arm evenwijdig aan zichzelf beweegt, het puntproduct van n en T 0 is).

de Stelling van Guldin

vervolgens gaan we proberen het gedrag van de planimeter intuïtief duidelijk te maken, maar eerst gaan we kijken naar een speciaal soort planimeter, en in dit geval een meer algemeen resultaat bewijzen. Stel dat we een enkele vrij bewegende arm van lengte l nemen en er een meetwiel van straal R aan bevestigen in het midden.

dan bewegen we de arm rond op het vlak. Als het meetwiel door een totale hoek van θ radialen draait terwijl de arm beweegt, is de afstand die een punt op de omtrek aflegt C = θR.

De Stelling van Guldin. In deze situatie is het totale oppervlak dat door de arm wordt weggevaagd het product lC.

gebied hier wordt geïnterpreteerd met een teken. Als de arm gewoon rond het midden draait, gaat de ene helft van de arm naar voren en de andere naar achteren, en de twee annuleren.

We hebben al gezien dat Guldin ‘ s bewering geldig is in het geval dat de arm enkel vertaalt. Natuurlijk gebeurt dit niet altijd – de arm kan draaien als hij beweegt en vertalen. Maar we kunnen zien wat er gebeurt door het geveegd gebied als volgt te hakken:

omdat het meetwiel zich in het midden van de arm bevindt, drukt het de kleine blokken aan de ene kant samen terwijl het ze aan de andere kant uitzet. Deze effecten neutraliseren elkaar precies.

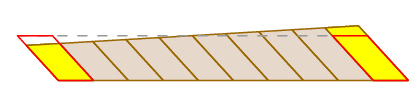
een volledig rigoureus bewijs kan worden geleverd door gebruik te maken van de formule voor verandering van variabelen in een dubbele integraal en de uitdrukking voor wielweg als een padintegraal.

stel nu dat het wiel ergens anders wordt geplaatst. Stel dat de positie c + v is waar c het centrum van de arm is, en v een vector langs de arm. De lengte van v blijft vast, bijvoorbeeld bij ρ. Het pad dat het wiel volgt is c(t) + v (t). De padintegraal is nu

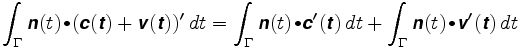
de eerste integraal is de afstand die het wiel zou afleggen als het zich in het midden van de arm bevond. In de tweede staat de vector v(t) altijd loodrecht op n, en heeft v(t) een constante lengte. De vector v (t) beweegt zich rond op een straalcirkel gelijk aan ρ. Daarom is het puntproduct van n en v ‘(t) gewoon de ondertekende lengte van v'(t), en de tweede integraal is gelijk aan ρ maal de totale rotatie van de arm. Vandaar:

als het wiel zich op afstand ρ van het midden van de arm bevindt, is de afstand C die het wiel meet C0 , de afstand die zou worden gemeten als het wiel zich in het midden bevond, plus ρ maal de totale hoek θ waarin de arm draait.

u kunt onmiddellijk een eenvoudig geval hiervan zien door de arm om het midden te draaien. Als we dit combineren met de Stelling van Guldin, zien we dat in alle gevallen:

c = C0 + ρ θ
oppervlakte weggevaagd = l C0 = l C – L ρ θ

het volledige resultaat

Guldin ‘ s formule geeft een getekende oppervlakte-als je achterwaarts over een gebied veegt, gaat het wiel achteruit en annuleer je gebied dat je al hebt bedekt. Als we dit toepassen op het geval waar de vrije arm precies terug komt naar waar het begon, zien we dat lC gelijk is aan de oppervlakte van het gesloten gebied dat wordt getraceerd door het rechter uiteinde van de arm minus die van het gebied dat wordt weggevaagd door de linker.

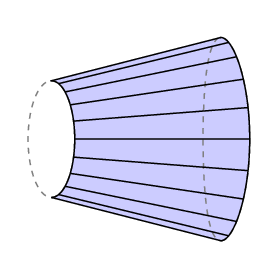
in het geval van de polaire planimeter is de onderkant van de arm beperkt tot een boog van de cirkel met straal r met een middelpunt op de pool, vandaar dat L C het gebied is dat door de tracer wordt getraceerd. Bovendien ligt de pool normaal gesproken buiten het te meten gebied, en in dit geval moet de totale rotatie van de arm 0 zijn. Dus in dit geval hebben we

oppervlakte van de regio getraceerd = lC

Hier is de figuur opgenomen door Jakob Amsler, de uitvinder, in zijn oorspronkelijke artikel over het instrument dat hij uitvond:

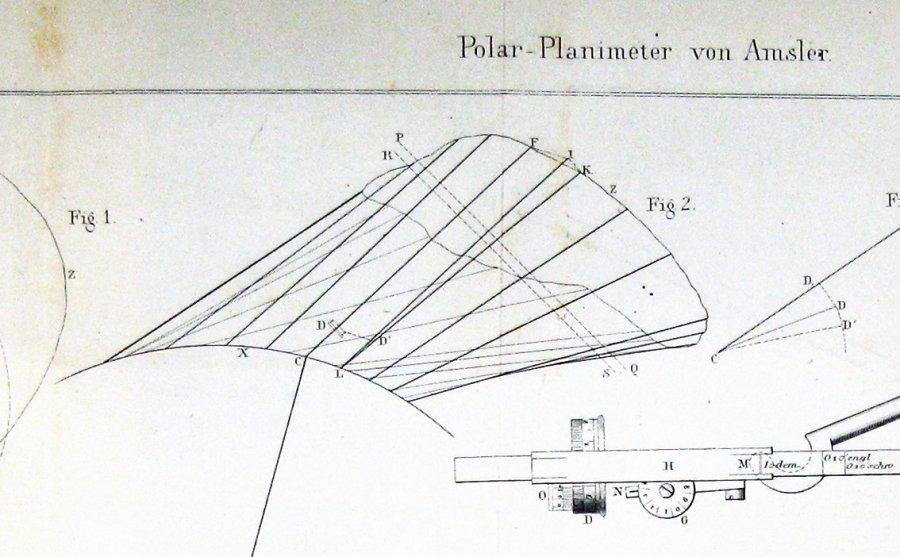
Het lijkt vrij duidelijk dat Amsler zijn constructie ontleende aan een of andere vorm van de stelling van Guldin.

Planimeters en de Stelling van Green

zoals we al hebben gezegd, is de planimeterconfiguratie een continue functie van de positie van de tracer. Stel dat we de positieve oriëntatie kiezen. Dan kunnen we aan elk punt van de annulus een eenheidsvector n bevestigen, die tegen de klok in wijst en loodrecht staat op de tracerarm bij de tracer.

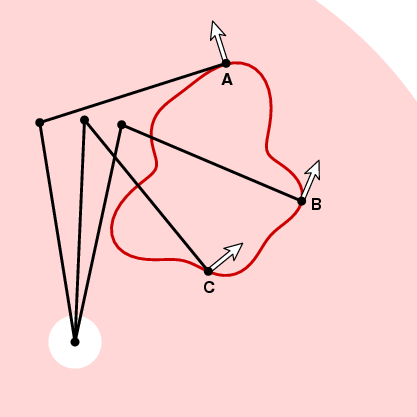
hoe het meetwiel zal reageren op beweging langs de kromme in het volgende moment hangt af van de hoek tussen deze vector en de eenheidsraakvector van de kromme. Bij A in de afbeelding hierboven gaat het meetwiel niet bewegen omdat de beweging langs de curve evenwijdig is aan de tracerarm. Bij B als de tracer een kleine afstand DS beweegt, zal het meetwiel dat ook doen. En bij C beweegt het meetwiel enige afstand tussen 0 en ds. Om precies te zijn, stel dat t de eenheidsraakvector is op een bepaald punt van de kromme. Als de tracer afstand ds langs de curve beweegt, zal op dat punt het meetwiel een afstand D ds bewegen, waarbij d = n . t, het puntproduct van de eenheidsvectoren t en n. met andere woorden, als we rondom de kromme Γ bewegen, zal het meetwiel een totale afstand bewegen die gelijk is aan de integraal van n . t ds (dot product), of

maar omdat elk punt van de annulus overeenkomt met een unieke positieve configuratie van de planimeter, kunnen we een vector n toewijzen aan elk interieur punt van de annulus, en daarom definieert het een vectorveld. De Kromme Γ is de grens van zijn inwendige Ω, en door een van onze veronderstellingen is dit volledig opgenomen in het gebied waar n is gedefinieerd. De Stelling van Green vertelt ons dat de integraal van het pad rond de grens van dit gebied ook gelijk is aan een bepaalde integraal Over Ω: Daarom vertelt De Stelling van Green ons dat

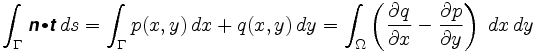
waarbij n = het betrokken vectorveld is. De integrand in de dubbele integraal wordt de krul van het vectorveld genoemd.

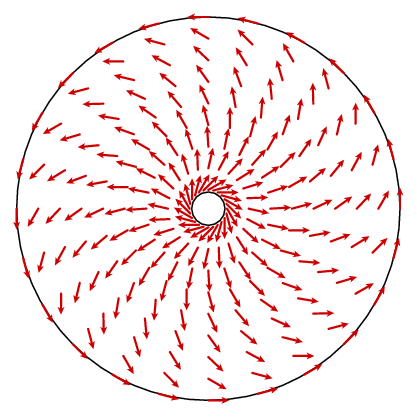
Dit lijkt ons niet erg ver te brengen. Wat er zou moeten gebeuren is dat de krul een constante 1 is. In principe kunnen we een formule vinden voor het vectorveld n en de krul berekenen, maar dat is niet erg verhelderend. We kunnen echter profiteren van een ander feit. Het vectorveld heeft cirkelvormige symmetrie, wat betekent dat het wordt bepaald door wat het op één straal is. De cosinus wet geeft ons een eenvoudige formule voor de omtrekcomponent.

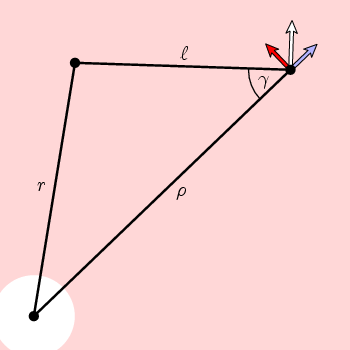
uit de eenvoudige meetkunde in deze figuur volgt dat de circumferentiële component van n

f(ρ) = cos(γ) = (ρ 2 + l 2 – r 2)/(2 ρ l)

het reële punt van de Stelling van Green is dat om te controleren of de integrand 1 is, het volstaat om te controleren of de integraal van het pad rond geschikte kleine paden de hetzelfde als het gebied. Hiervoor kiezen we onze regio ‘ s om zo hier te zijn:

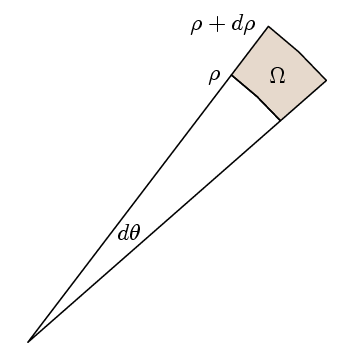
dan L keer de integraal van het pad is

l (ρ + dp) (f(ρ+dp) – f(ρ)) dθ

of

(θ/2) ((ρ + dp) 2 – ρ 2)

wat de oppervlakte van de regio Ω is.

andere soorten planimeters

De Stelling van Guldin impliceert dat de beweging van een meetwiel u het door de tracer getraceerde gebied zal vertellen wanneer de arm met een meetwiel erop een kromme traceert maar één uiteinde beperkt heeft tot een eendimensionale kromme. Dit gebeurt bijvoorbeeld met de rolplanimeter, waarbij het draaipunt tot een rechte lijn wordt beperkt door zich op een rolcilinder te bevinden.

om meer te weten te komen

• maakt en verkoopt nog steeds planimeters.
• Differential and Integral Calculus Volume II, R. Courant, Blackie & Son, 1936. De sectie over Guldin ‘ s Formule (PP.294-298) geeft een uitleg van hoe de planimeter werkt.het oorspronkelijke artikel van Amsler, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Hier ontbreken de diagrammen, maar ze zijn hier:
  • Amsler ’s eerste diagram
  • Amsler’ s tweede diagram

  onze dank aan Donna Sammis van de Stony Brook University Library voor het lokaliseren van het artikel en aan haar echtgenoot Robert voor het leveren van foto ‘ s van de figuren.het bedrijf dat Amsler oprichtte, produceerde tot ver in de 20e eeuw instrumenten. Deze foto toont het logo op een stroomafnemerversie van de planimeter:

  

• “over Planimeters,” EngineerSupply. Het bedrijf heeft ook een video op YouTube geplaatst.

Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca

John Eggers
University of California, San Diego
jeggers at ucsd.edu

degenen die toegang hebben tot JSTOR kunnen enkele van de hierboven genoemde papers daar vinden. Voor degenen die toegang hebben, kan het MathSciNet van de American Mathematical Society worden gebruikt om aanvullende bibliografische informatie en reviews van sommige van deze materialen te krijgen. Sommige van de bovenstaande items zijn toegankelijk via de ACM Portal, die ook bibliografische diensten biedt.