
Een Kunstmatig Neuraal Netwerk (ANN) is gemaakt van de vele onderling verbonden neuronen:
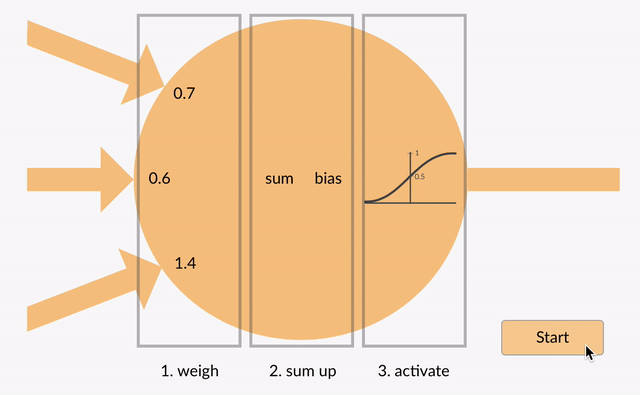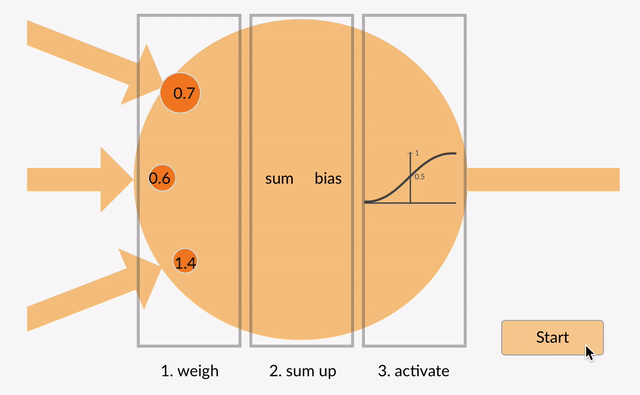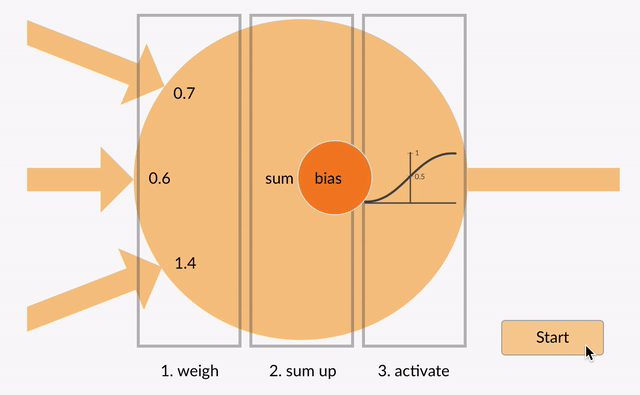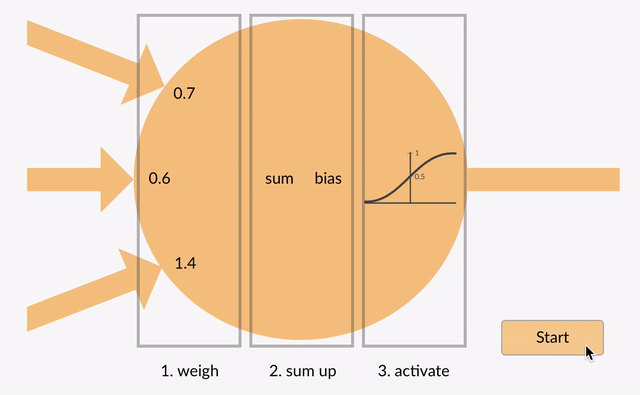
Elk neuron neemt in sommige floating point getallen (bijv. 1.0, 0.5, -1.0) en vermenigvuldigt ze met enkele andere drijvende-kommagetallen (bijvoorbeeld 0,7, 0,6, 1,4) die bekend staan als gewichten (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). De gewichten fungeren als een mechanisme om zich te concentreren op, of te negeren, bepaalde inputs.

Het gewogen ingangen vervolgens bij elkaar opgeteld (bijv. 0.7 + 0.3 + -1.4 = -0.4) samen met een bias waarde (bijvoorbeeld -0,4 + -0,1 = -0,5).
de samengevoegde waarde (x) wordt nu omgezet in een uitgangswaarde (y) volgens de activeringsfunctie van het neuron (y = f(x)). Sommige populaire activering functies worden hieronder getoond:

bijvoorbeeld -0.5 → -0.05 als we het Lek Verholpen Lineaire Eenheid (Lekkende ReLU) activering van de functie: y = f(x) = f(-0.5) = max(0.1*-0.5, -0.5) = max(-0.05, -0.5) = -0.05
de uitgangswaarde van het neuron (bijvoorbeeld -0,05) is vaak een input voor een ander neuron.
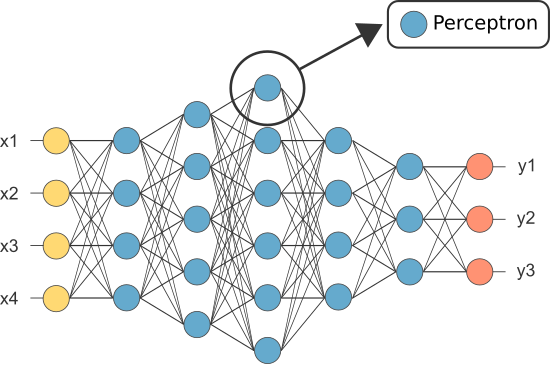
Echter, een van de eerste armen hingen langs was bekend als het perceptron en het bestond uit slechts een enkel neuron.

De output van het (enige) Neuron van de percepttron fungeert als de laatste voorspelling.

laat onze eigen perceptron coderen:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(Nota: wij zijn niet inbegrepen eventuele learning algoritme in ons voorbeeld — wij bestrijken het leren van algoritmes in een andere tutorial)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

dus waarom hebben we zoveel neuronen nodig in een ANN als er één voldoende is (als classifier)?

helaas zijn individuele neuronen alleen in staat om lineair scheidbare gegevens te classificeren.

echter, door neuronen te combineren, combineren we in wezen hun beslissingsgrenzen. Daarom is een ANN samengesteld uit vele neuronen in staat om complexe, niet-lineaire beslissingsgrenzen te leren.

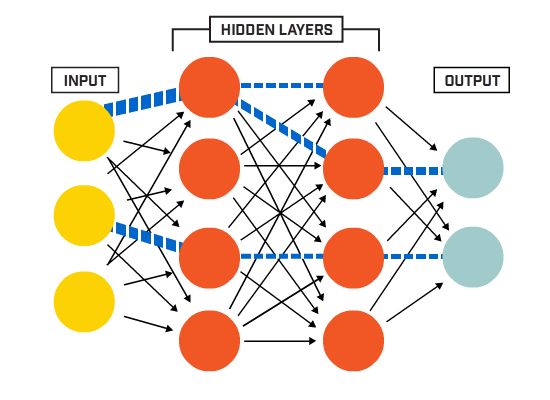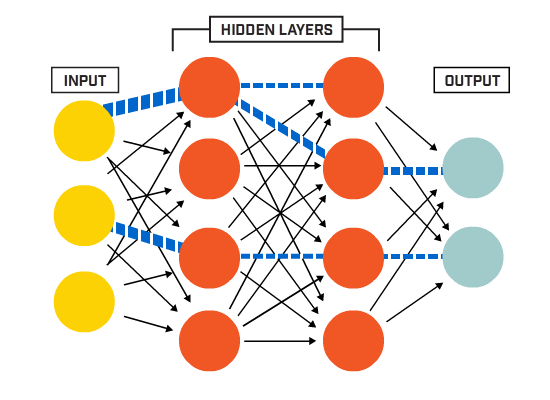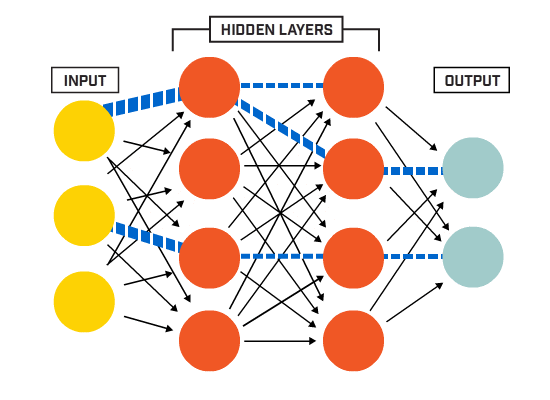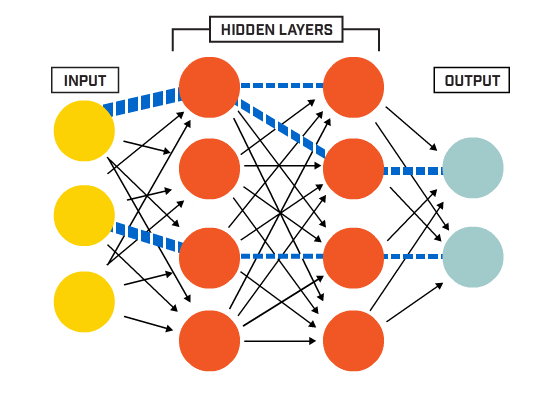
neuronen zijn met elkaar verbonden volgens een specifieke netwerkarchitectuur. Hoewel er verschillende architecturen zijn, bevatten ze bijna allemaal lagen. (NB: Neuronen in dezelfde laag niet verbinden met elkaar).
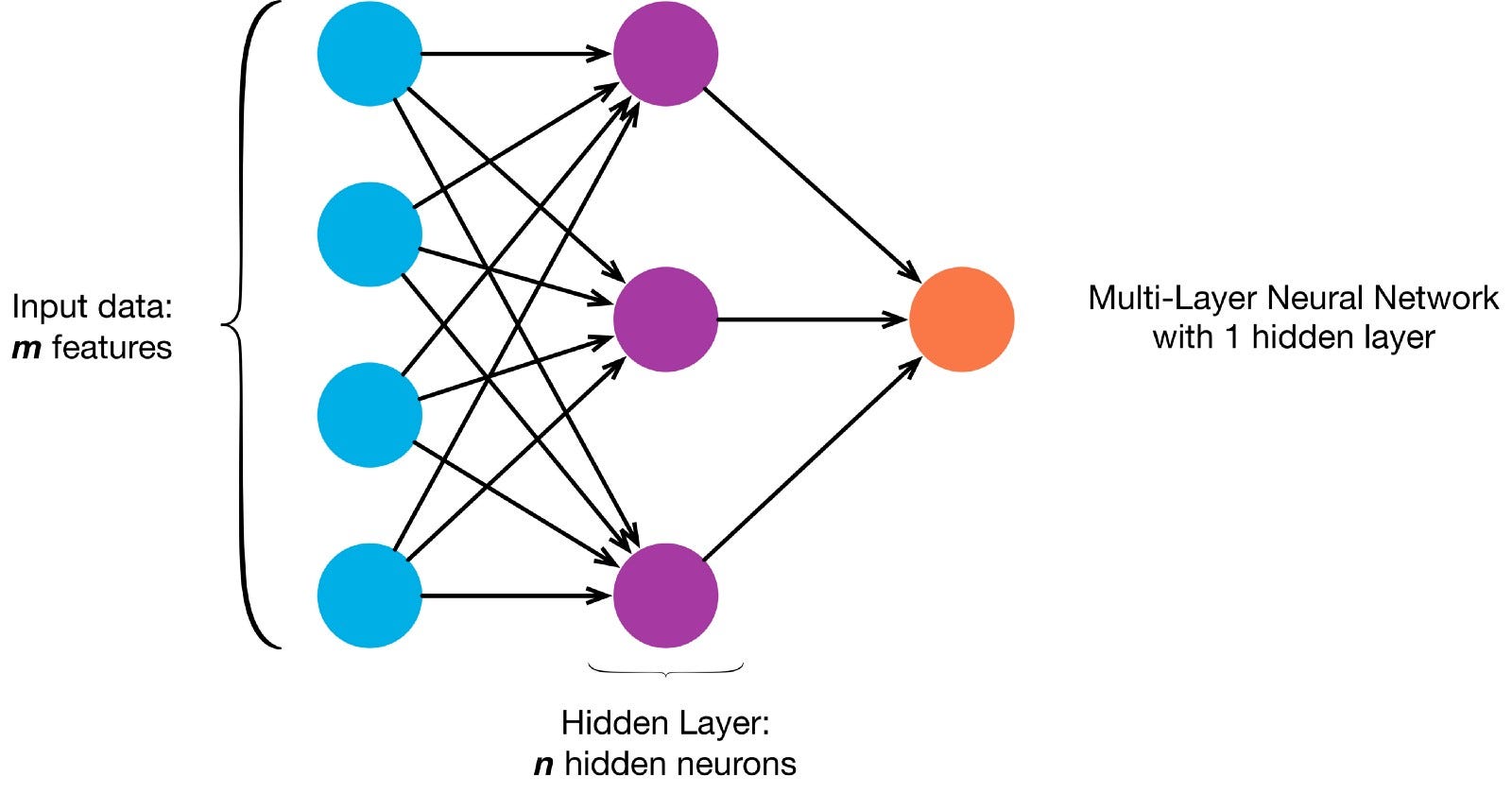
Er is meestal een input-laag (met een aantal neuronen gelijk aan het aantal input functies in de gegevens), een uitgang laag (met een aantal neuronen gelijk aan het aantal klassen) en een verborgen laag (met een willekeurig aantal neuronen).

Er kan meer dan één verborgen laag zijn om het neurale net in staat te stellen complexere beslissingsgrenzen te leren (elk neuraal net met meer dan een verborgen laag wordt beschouwd als een diep neuraal net).
laten we een diepe NN maken om deze afbeelding te tekenen:

hier Kunt downloaden van de afbeelding en het laden van de pixels in een array
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
Nu leer ons ANN schilderen is een begeleid leren taak, dus we moeten maken van een etiket voorzien opleiding ingesteld (Onze training gegevens heeft ingangen en de verwachte output etiketten voor elke ingang). De trainingsingangen hebben 2 waarden (de X,y coördinaten van elke pixel).
gezien de eenvoud van de afbeelding, kunnen we dit probleem op twee manieren benaderen. Een classificatieprobleem (waarbij het neurale net voorspelt of een pixel behoort tot de” blauwe “klasse of de” grijze ” klasse, gegeven zijn xy coördinaten) of een regressie probleem (waarbij het neurale net voorspelt RGB waarden voor een pixel gegeven zijn coördinaten).
als dit wordt behandeld als een regressieprobleem: de trainingsresultaten zullen 3 waarden hebben (de genormaliseerde r,g,b-waarden voor elke pixel). – Laten we deze methode gebruiken voor nu.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
Nu kunt maken van onze ANN:

- Het moet 2 neuronen in de input laag (omdat er 2 waarden te nemen: x & y-coördinaten).
- Het zou 3 neuronen in de uitvoerlaag moeten hebben (aangezien er 3 waarden zijn om te leren: r, g, b).
- het aantal verborgen lagen en het aantal neuronen in elke verborgen laag zijn twee hyperparameters om mee te experimenteren (evenals het aantal tijdperken waarvoor we het zullen trainen, de activeringsfunctie, enz.) — Ik zal 10 verborgen lagen gebruiken met 100 neuronen in elke verborgen laag (waardoor dit een diep neuraal netwerk is)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
het getrainde netwerk kan nu de genormaliseerde RGB-waarden voorspellen voor elke coördinaten (bijv. x,y = 1,1).
ann.predict(])
array(])
laten we de ANN om het voorspellen van de rgb-waarden voor elk coördinaat en laat het display de voorspelde rgb-waarden voor het gehele beeld om te zien hoe goed het deed (kwalitatief — we laten de evaluatie-gegevens voor een andere tutorial)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

Probeer het wijzigen van de hyperparameters om betere resultaten te krijgen.
Als in plaats van het behandelen dit als een regressie probleem, wij beschouwen dit als een classificatie probleem, dan is de training uitgangen hebben 2 waarden (de waarschijnlijkheid van de pixel die behoren bij elk van de twee klassen: de “blauwe” en “grijze”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
We kunnen de wederopbouw van ons ANN als een binaire classifier met 2 neuronen in de invoerlaag 2 neuronen in de uitgang laag en 100 neuronen in de verborgen laag (met 10 verborgen lagen)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
We kunnen nu gebruik maken van de opgeleide ANN om het voorspellen van de klasse waarin elke pixel behoort (0: “grijs” of 1: “blauw”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: “grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

