in de praktijk van machine en deep learning zijn modelparameters de eigenschappen van trainingsgegevens die op zichzelf zullen leren tijdens de training door de classifier of een ander ML-model. Bijvoorbeeld, gewichten en vooroordelen, of split points in Decision Tree.
Model Hyperparameters zijn in plaats daarvan eigenschappen die het gehele trainingsproces bepalen. Ze omvatten variabelen die de netwerkstructuur bepalen (bijvoorbeeld het aantal verborgen eenheden) en de variabelen die bepalen hoe het netwerk wordt getraind (bijvoorbeeld Leersnelheid). Model hyperparameters worden ingesteld voor de training (voor het optimaliseren van de gewichten en bias).
bijvoorbeeld, hier zijn enkele model ingebouwde configuratievariabelen:
- Leersnelheid
- Aantal tijdperken
- verborgen lagen
- verborgen eenheden
- Activeringsfuncties
Hyperparameters zijn belangrijk omdat ze direct het gedrag van de trainingsalgo bepalen, wat een belangrijke invloed heeft op de prestaties van het model tijdens de training.
het kiezen van geschikte hyperparameters speelt een sleutelrol in het succes van neurale netwerkarchitecturen, gezien de impact op het geleerde model. Bijvoorbeeld, als het leerpercentage te laag is, zal het model de belangrijke patronen in de gegevens missen; omgekeerd, als het hoog is, kan het botsingen hebben.
het kiezen van goede hyperparameters biedt twee belangrijke voordelen:
- efficiënt zoeken in de ruimte van mogelijke hyperparameters; en
- eenvoudiger beheer van een grote reeks experimenten voor hyperparameterafstelling.
Hyperparameters kunnen ruwweg worden verdeeld in 2 categorieën:
1. Optimizer hyperparameters,
2. Modelspecifieke hyperparameters
ze houden meer verband met het optimalisatie-en opleidingsproces.
1.1. Leersnelheid:
als de leersnelheid van het model veel te kleiner is dan de optimale waarden, zal het veel langer duren (honderden of duizenden) tijdperken om een ideale toestand te bereiken. Aan de andere kant, als de leersnelheid veel groter is dan de optimale waarde, dan zou het de ideale toestand overschrijden en zou het algoritme niet convergeren. Een redelijke start Leersnelheid = 0,001.
belangrijk om te bedenken dat:
A) het model honderden en duizenden parameters zal hebben, elk met zijn eigen foutcurve. En Leersnelheid moet ze allemaal herleiden
b) foutcurves zijn geen schone u-vormen; in plaats daarvan hebben ze meestal complexere vormen met lokale minima.
1.2. Mini-Batchgrootte:
batchgrootte heeft op een niet-triviale manier invloed op de resourcevereisten van het trainingsproces, de snelheid en het aantal herhalingen.
historisch gezien is er een discussie geweest over stochastische training waarbij u een enkel voorbeeld van de dataset past bij het model en, gebruikmakend van slechts één voorbeeld, een forward pass uitvoert, de fout berekent / backpropagate & aangepaste waarden voor alle hyperparameters instelt. En doe dit dan opnieuw voor elk voorbeeld in de dataset.
of, misschien beter om de volledige gegevens aan de trainingsstap toe te voegen en de gradiënt te berekenen met behulp van de fout die wordt gegenereerd door te kijken naar alle voorbeelden in de dataset. Dit wordt batch training genoemd.
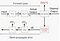
vaak gebruikte techniek vandaag is het instellen van een mini-batch grootte. Stochastische Training is wanneer de minibatch Maat =1, en Batch Training is wanneer de mini-batch maat = aantal voorbeelden in de training set. Aanbevolen startwaarden voor experimenten: 1, 2, 4, 8, 16, 32, 64, 128, 256.
een grotere mini-batchgrootte maakt computationele boosts mogelijk die gebruik maken van matrixvermenigvuldiging in de trainingsberekeningen . Het gaat echter ten koste van meer geheugen nodig voor het trainingsproces. Een kleinere mini-batchgrootte veroorzaakt meer ruis in foutberekeningen , vaak nuttiger om te voorkomen dat het trainingsproces stopt bij lokale minima. Een reële waarde voor mini-batchgrootte = 32.
dus, terwijl de computationele boost ons drijft om de mini-batchgrootte te vergroten, stimuleert dit praktische algoritmische voordeel om het eigenlijk kleiner te maken.
1.3. Aantal tijdperken:
om het juiste aantal tijdperken voor de trainingsstap te kiezen, moeten we letten op de validatiefout.
De intuïtieve handmatige manier is om de modeltrein voor zo veel aantal herhalingen zolang validatiefout blijft verminderen.
Er is een techniek die kan worden gebruikt met de naam Early stoping om te bepalen wanneer het trainen van het model moet worden gestopt; het gaat erom het trainingsproces te stoppen als de validatiefout in de afgelopen 10 of 20 tijdperken niet is verbeterd.
2. Model Hyperparameters
zij zijn meer betrokken bij de structuur van het model:
2.1. Aantal verborgen eenheden:
aantal verborgen eenheden is een van de meer mysterieuze hyperparameters. Laten we niet vergeten dat neurale netwerken universele functie-benaderingen zijn, en om te leren om een functie (of een voorspellingstaak) te benaderen , moeten ze voldoende ‘capaciteit’ hebben om de functie te leren kennen. Het aantal verborgen eenheden is de belangrijkste maatstaf voor het leervermogen van het model.
voor een eenvoudige functie heeft het mogelijk minder verborgen eenheden nodig. Hoe complexer de functie, hoe meer leercapaciteit het model nodig heeft.
iets meer aantal eenheden dan het optimale aantal is geen probleem, maar een veel groter aantal zal leiden tot overfitting (d.w.z. Als u een model met te veel capaciteit voorziet, kan het de neiging hebben om de dataset te “onthouden”, waardoor de capaciteit om te generaliseren wordt beïnvloed)
2.2. Eerste Verborgen laag:
een andere heuristiek met betrekking tot de eerste Verborgen laag is dat het instellen van het aantal verborgen eenheden groter is dan het aantal inputs, volgens empirische observatie betere resultaten in het aantal taken mogelijk maakt.
2.3. Aantal lagen:
Het is vaak het geval dat neuraal netwerk met 3 lagen beter zal presteren dan een neuraal netwerk met 2 lagen. Maar nog dieper gaan helpt zelden veel meer. (uitzondering zijn convolutionele neurale netwerken, waar hoe dieper ze zijn, hoe beter ze presteren).
hyperparameters optimalisatietechnieken
het proces om de meest optimale hyperparameters te vinden in machine learning wordt hyperparameteroptimalisatie genoemd.
gemeenschappelijke algoritmen omvatten:
- Rasterzoek
- Random Search
- Bayesiaanse optimalisatie
Rasterzoek
Rasterzoek is een traditionele techniek voor het implementeren van hyperparameters. Het gaat een beetje over brute kracht alle combinaties. Raster zoeken vereist het creëren vantwee set van hyperparameters:
- Leersnelheid
- aantal lagen
Grid search traint het algoritme voor alle combinaties met behulp van de twee set hyperparameters (Leersnelheid en aantal lagen) en meet de prestaties met behulp van kruisvalidatietechniek. Deze validatietechniek zorgt ervoor dat het getrainde model de meeste patronen uit de dataset haalt (een van de beste methoden om validatie uit te voeren met behulp van “K-Fold Cross Validation” die helpt om voldoende gegevens te verschaffen voor het trainen van het model en voldoende gegevens voor validaties).
De Rasterzoekmethode is een eenvoudiger algoritme om te gebruiken, maar het lijdt als gegevens een hoge dimensionale ruimte hebben die de vloek van dimensionaliteit wordt genoemd.
willekeurig zoeken
willekeurig monsters van de zoekruimte en evalueert sets uit een gespecificeerde kansverdeling. In plaats van alle 100.000 monsters te controleren, bijvoorbeeld, kunnen we 1.000 willekeurige parameters controleren.
het nadeel van het willekeurige zoekalgoritme is echter dat het geen informatie uit eerdere experimenten gebruikt om de volgende set te selecteren. Bovendien is het moeilijk om de volgende experimenten te voorspellen.

Bayesian optimalisatie
hyperparameter instelling maximaliseert de prestaties van het model op een validatieset. ML algos vereisen vaak fine-tuning van model hyperparameters. Helaas wordt die afstemming vaak ‘zwarte functie’ genoemd omdat het niet in een formule kan worden geschreven (afgeleiden van de functie zijn onbekend).
een aantrekkelijker manier om & hyperparameters af te stellen, houdt in dat geautomatiseerde modelafstemming mogelijk wordt-bijvoorbeeld door Bayesiaanse optimalisatie te gebruiken. Het model dat wordt gebruikt voor het benaderen van de objectieve functie wordt surrogaatmodel genoemd. Een populair surrogaatmodel voor Bayesiaanse optimalisatie is Gaussian process (GP). Bayesiaanse optimalisatie werkt meestal door aan te nemen dat de onbekende functie werd bemonsterd uit een Gaussiaans proces (GP) en handhaaft een posterieure verdeling voor deze functie als waarnemingen worden gedaan.
Er zijn twee belangrijke keuzes die gemaakt moeten worden bij het uitvoeren van Bayesiaanse optimalisatie:
- selecteer functies die voorafgaan aan functies die veronderstellingen weergeven over de functie die geoptimaliseerd wordt. Hiervoor kiezen we Gaussian Process prior;
- vervolgens moeten we een acquisitiefunctie kiezen die wordt gebruikt om een utiliteitsfunctie te construeren uit het model posterior, zodat we het volgende te evalueren punt kunnen bepalen.
Gaussiaans proces
een Gaussiaans proces definieert de eerdere verdeling over functies die kan worden omgezet in een posterieure over functies zodra we enkele gegevens hebben gezien. Het Gaussiaanse proces maakt gebruik van covariantie matrix om ervoor te zorgen dat waarden die dicht bij elkaar liggen. De covariantiematrix samen met een gemiddelde µ-functie om de verwachte waarde F(x) uit te voeren definieert een Gaussiaans proces.
1. Gaussiaans proces zal gebruikt worden als een prior voor Bayesiaanse gevolgtrekking;
2. Het berekenen van de posterieure maakt het mogelijk om voorspellingen te doen voor ongeziene testcases.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Populaire acquisitiefuncties zijn
- maximale kans op verbetering (MPI)
- verwachte verbetering (EI)
- Upper Confidence Bound (UCB)
De verwachte verbetering (EI) is een populaire en gedefinieerd als:
EI(x)=𝔼
waarbij ƒ(x ) de huidige optimale set hyperparameters is. Het maximaliseren van de hyperparameters zal verbeteren op ƒ.
