Inleiding tot Bewegingsschatting met optische Flow

in deze handleiding duiken we in de fundamenten van optische Flow, kijken we naar enkele van de toepassingen ervan en implementeren we de twee belangrijkste varianten (dun en dicht). We bespreken ook kort meer recente benaderingen met behulp van deep learning en veelbelovende toekomstige richtingen.

recente doorbraken in computervisieonderzoek hebben machines in staat gesteld de omringende wereld waar te nemen door middel van technieken zoals objectdetectie voor het detecteren van instanties van objecten die tot een bepaalde klasse behoren en semantische segmentatie voor pixel-wise classificatie.

echter, voor het verwerken van real-time video-invoer, richten de meeste implementaties van deze technieken zich alleen op relaties van objecten binnen hetzelfde frame \((x, y)\) zonder rekening te houden met tijdinformatie \((t)\). Met andere woorden, ze her-evalueren elk frame onafhankelijk, alsof het volledig ongerelateerde beelden, voor elke run. Maar wat als we de relaties tussen opeenvolgende frames nodig hebben, bijvoorbeeld, we willen de beweging van voertuigen over frames volgen om de huidige snelheid te schatten en de positie in het volgende frame te voorspellen?

of, als alternatief, wat als we informatie nodig hebben over menselijke pose relaties tussen opeenvolgende frames om menselijke handelingen zoals Boogschieten, Honkbal en basketbal te herkennen?

In deze tutorial zullen we leren wat Optical Flow is, hoe de uitvoering van zijn twee belangrijke varianten (dun en dik), en ook een grote foto van een meer recente benaderingen waarbij diep leren en veelbelovende toekomst routebeschrijvingen.

Wat is optische stroom?
implementatie van dunne optische Flow
implementatie van dichte optische Flow
Deep learning en verder

Wat is optische flow?

laten we beginnen met een begrip van optische flow op hoog niveau. Optische stroom is de beweging van objecten tussen opeenvolgende frames van volgorde, veroorzaakt door de relatieve beweging tussen het object en de camera. Het probleem van de optische stroom kan worden uitgedrukt als:

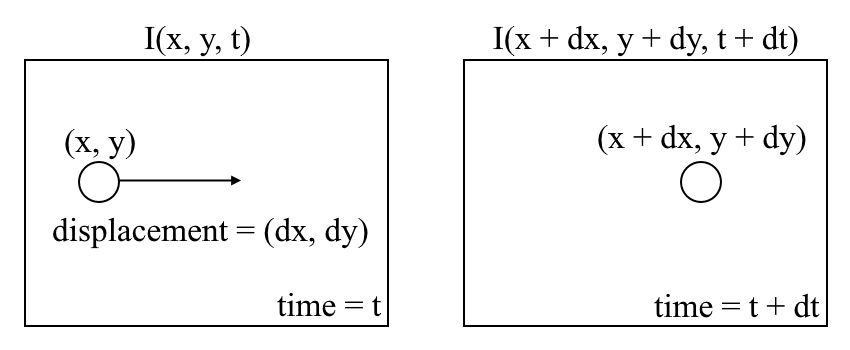
waar tussen opeenvolgende frames de afbeeldingsintensiteit \((i)\) kan worden uitgedrukt als functie van ruimte \((x, y)\) en tijd \((t)\). Met andere woorden, als we de eerste afbeelding \(I(X, y, t)\) nemen en de pixels verplaatsen met \((dx, dy)\) over \(t\) tijd, krijgen we de nieuwe afbeelding \(I(x + dx, y + dy, t + dt)\).

ten eerste nemen we aan dat pixelintensiteiten van een object constant zijn tussen opeenvolgende frames.

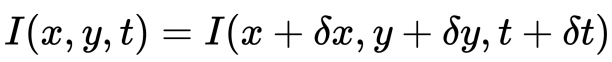
ten tweede nemen we de Taylor-serie benadering van de RHS en verwijderen we gemeenschappelijke termen.

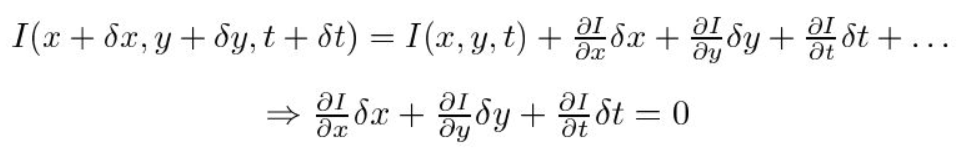
Ten derde delen we door \(dt\) om de optische stroomvergelijking af te leiden:

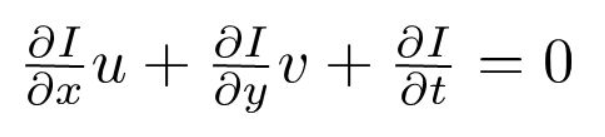
waarbij \(u = dx/dt\) en \(v = dy / dt\).

\(dI/dx, dI/dy\), en \(dI / dt\) zijn de gradiënten van de afbeelding langs de horizontale as, de verticale as en de tijd. Vandaar dat we besluiten met het probleem van optische stroom, dat wil zeggen het oplossen van \(u (dx/dt)\) en \(v (dy/dt)\) om beweging in de tijd te bepalen. Je zult merken dat we de optische stroomvergelijking voor \(u\) en \(v\) niet direct kunnen oplossen omdat er maar één vergelijking is voor twee onbekende variabelen. We zullen een aantal methoden implementeren, zoals de Lucas-Kanade methode om dit probleem aan te pakken.

Sparse vs Dense Optical Flow

Sparse optical flow geeft de stroomvectoren van enkele “interessante eigenschappen” (bijvoorbeeld enkele pixels die de randen of hoeken van een object weergeven) binnen het frame, terwijl dichte optische flow, die de stroomvectoren van het gehele frame (alle pixels) geeft – tot één stroomvector per pixel. Zoals je zou hebben geraden, dichte optische stroom heeft een hogere nauwkeurigheid ten koste van het zijn langzaam / computationeel duur.

Implementing Sparse Optical Flow

Sparse optical flow selecteert een sparse feature set van pixels (bijvoorbeeld interessante features zoals randen en hoeken) om de snelheidsvectoren (beweging) te volgen. De geëxtraheerde functies worden doorgegeven in de optische flow-functie van frame naar frame om ervoor te zorgen dat dezelfde punten worden gevolgd. Er zijn verschillende implementaties van sparse optical flow, waaronder de Lucas-Kanade methode, De Horn–Schunck methode, de Buxton–Buxton methode, en meer. We zullen de Lucas-Kanade methode gebruiken met OpenCV, een open source bibliotheek van computer vision algoritmes, voor implementatie.

uw omgeving instellen

als OpenCV nog niet geïnstalleerd is, Open Terminal en voer uit:

pip install opencv-python

nu, clone de tutorial repository door het uitvoeren van:

git clone https://github.com/chuanenlin/optical-flow.git

volgende, open sparse-starter.py met je Teksteditor. We zullen alle code in dit Python bestand schrijven.

OpenCV configureren om een video te lezen en parameters instellen

shi-Tomasi Corner Detector – de pixels selecteren om

te volgen voor de implementatie van sparse optical flow, volgen we alleen de beweging van een feature set van pixels. Functies in afbeeldingen zijn punten van belang die rijke beeld inhoud informatie te presenteren. Dergelijke functies kunnen bijvoorbeeld punten in de afbeelding zijn die invariant zijn voor vertaling, schaal, rotatie en intensiteitsveranderingen zoals hoeken.

De shi-Tomasi Hoekdetector is zeer vergelijkbaar met de populaire Harris Hoekdetector die kan worden geïmplementeerd door de volgende drie procedures:

1. bepaal vensters (kleine beeldvlakken) met grote gradiënten (variaties in beeldintensiteit) wanneer vertaald in zowel \(x\) als \(y\) richtingen.
2. bereken voor elk venster een score \(R\).
3. afhankelijk van de waarde van \(R\) wordt elk venster geclassificeerd als plat, rand of hoek.

Als u meer wilt weten over een stap-voor-stap wiskundige uitleg van de Harris Corner Detector, aarzel dan niet om door deze dia ‘ s te gaan.

Shi en Tomasi maakten later een kleine maar effectieve aanpassing aan de Harris Corner Detector in hun papier goede eigenschappen te volgen.

de wijziging is de vergelijking waarin score \(R\) wordt berekend. In de Harris Hoekdetector wordt de scorefunctie gegeven door:

$$
\begin{array}{c}{R=\operatorname{det} M-k(\operatorname{trace} M)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$

in Plaats daarvan, Shi-Tomasi voorgesteld de score-functie, zoals:

$$
R=\min \left(\lambda_{1}, \lambda_{2}\right)
$$

dit betekent dat als \(R\) groter is dan een bepaalde drempel, wordt het geclassificeerd als een hoek. Het volgende vergelijkt de scoringsfuncties van Harris (links) en Shi-Tomasi (rechts) in \(λ1-λ2\) ruimte.

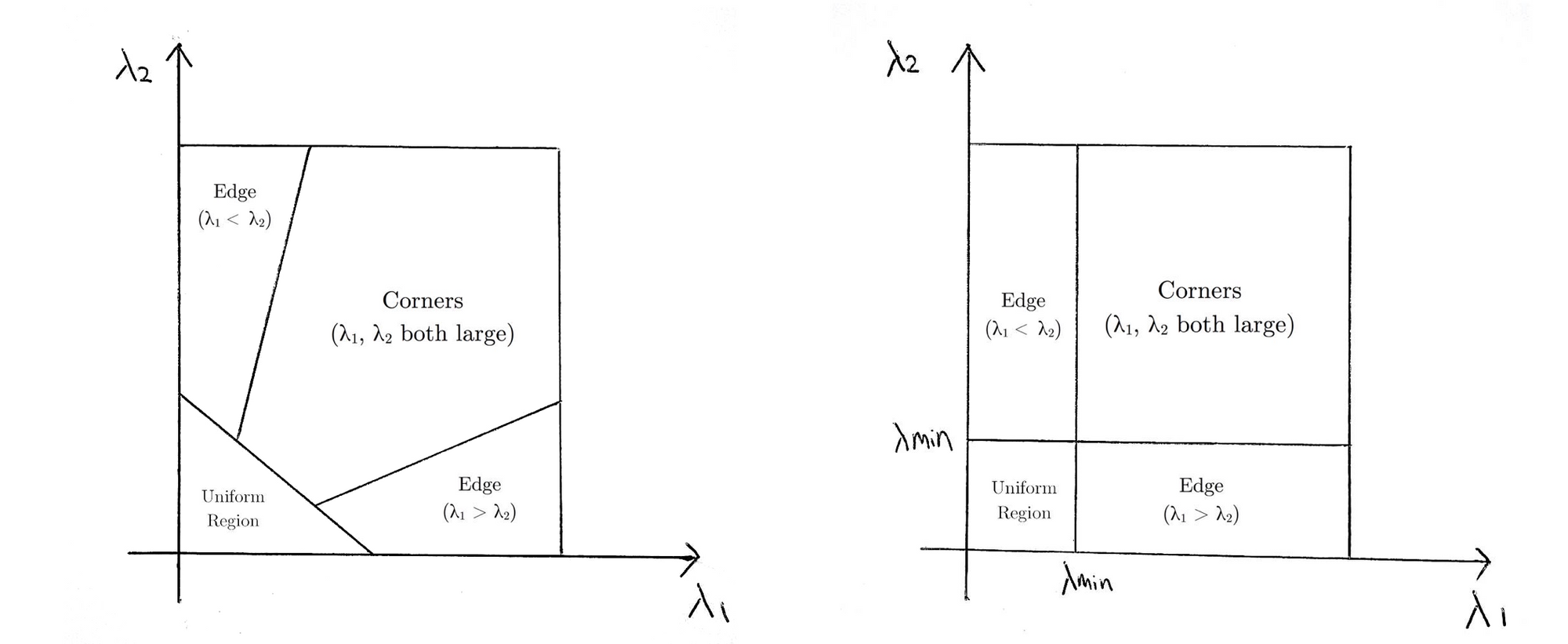
Voor Shi-Tomasi wordt het venster alleen geclassificeerd als \(λ1\) en \(λ2\) boven een minimumdrempel \(λmin\) liggen.

de documentatie van OpenCV ’s implementatie van Shi-Tomasi via goodFeaturesToTrack() kan hier worden gevonden.

specifieke objecten volgen

Er kunnen scenario ‘ s zijn waarin u alleen een specifiek object wilt volgen (bijvoorbeeld een bepaalde persoon volgen) of een categorie objecten (zoals alle Tweewielers in het verkeer). U kunt de code eenvoudig wijzigen om de pixels van het object(en) te volgen door de variabele prev te wijzigen.

U kunt objectdetectie ook combineren met deze methode om alleen de stroom van pixels binnen de gedetecteerde bounding boxes te schatten. Op deze manier kunt u alle objecten van een bepaald type/categorie in de video volgen.

Lucas-Kanade: Sparse Optical Flow

Lucas en Kanade stelden een effectieve techniek voor om de beweging van interessante eigenschappen te schatten door twee opeenvolgende frames in hun paper een iteratieve Beeldregistratietechniek te vergelijken met een toepassing op Stereo Vision. De Lucas-Kanade methode werkt onder de volgende veronderstellingen:

1. twee opeenvolgende frames worden gescheiden door een kleine tijdverhoging (\(dt\)) zodat objecten niet significant worden verplaatst (met andere woorden, de methode werkt het beste met langzaam bewegende objecten).
2. een frame toont een “natuurlijke” scène met gestructureerde objecten die grijstinten vertonen die soepel veranderen.

ten eerste, onder deze aannames, kunnen we een klein 3×3 venster (buurt) nemen rond de eigenschappen die door Shi-Tomasi worden gedetecteerd en aannemen dat alle negen punten dezelfde beweging hebben.

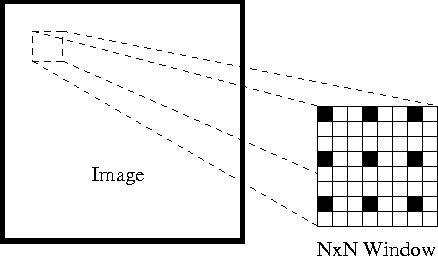
Dit kan worden weergegeven als

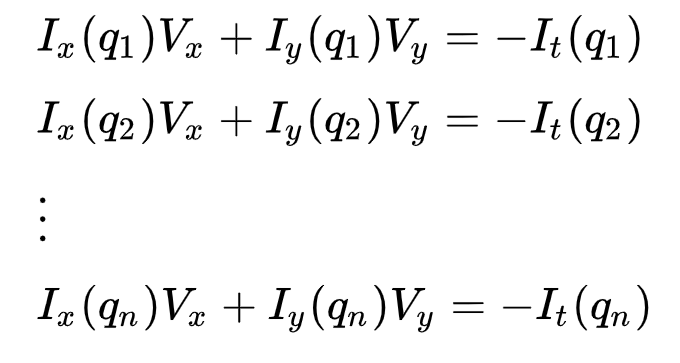
waar \(q_1, q_2, …, q_n\) geven de pixels binnen het venster (bijvoorbeeld \(n\) = 9 voor een 3×3-venster) en \(I_x(q_i)\), \(I_y(q_i)\) en \(I_t(q_i)\) geven de partiële afgeleiden van image \I\) met betrekking tot de positie \((x, y)\) en tijd \(t\), voor pixel \(q_i\) bij de huidige tijd.

Dit is gewoon de optische Stroomvergelijking (die we eerder beschreven) voor elk van de n pixels.

de verzameling vergelijkingen kan worden weergegeven in de volgende matrixvorm waarin \(Av = b\):

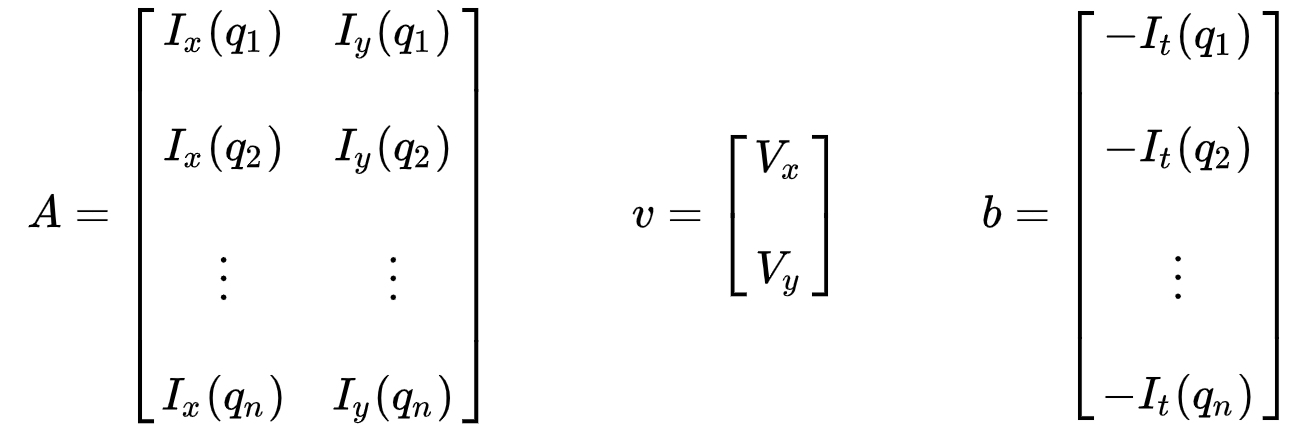
merk op dat eerder (zie “Wat is optische stroom?”sectie), we geconfronteerd met de kwestie van het hebben op te lossen voor twee onbekende variabelen met één vergelijking. We worden nu geconfronteerd met het oplossen van twee onbekenden (\(V_x\) en \(V_y\)) met negen vergelijkingen, die over-bepaald zijn.

ten Tweede, om de over-bepaald probleem, we passen de kleinste kwadraten montage te verkrijgen in de volgende twee-vergelijking-twee-onbekend probleem:

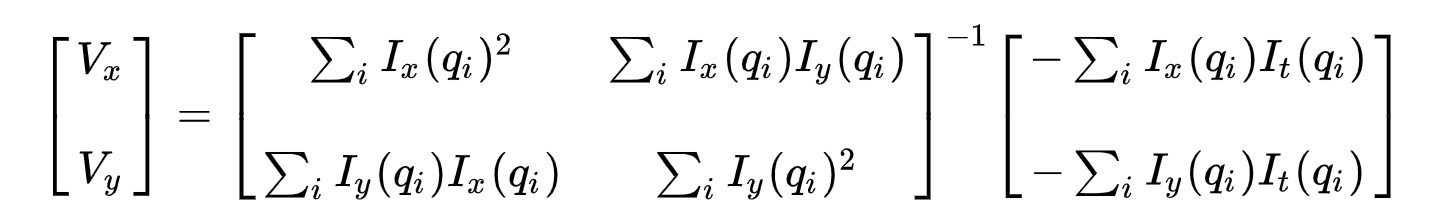
waar \(Vx = u = dx/dt\) geeft de beweging van \(x\) over tijd en \(Vy = v = dy/dt\) geeft de beweging van y in de tijd. Het oplossen van de twee variabelen completeert het optische stroomprobleem.

In een notendop identificeren we enkele interessante functies om de optische stroomvectoren van deze punten te volgen en iteratief te berekenen. Echter, het gebruik van de Lucas-Kanade methode werkt alleen voor kleine bewegingen (vanuit onze eerste aanname) en faalt als er grote beweging is. Daarom neemt de OpenCV-implementatie van de Lucas-Kanade-methode piramides aan.

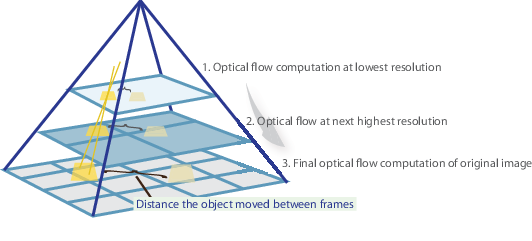
in een weergave op hoog niveau worden kleine bewegingen verwaarloosd terwijl we de piramide op gaan en worden grote bewegingen gereduceerd tot kleine bewegingen-we berekenen optische stroom samen met schaal. Een uitgebreide wiskundige uitleg van OpenCV ’s implementatie kan worden gevonden in bouguet’ s notities en de documentatie van OpenCV ‘ s implementatie van de Lucas-Kanade methode via calcOpticalFlowPyrLK() kan hier worden gevonden.

visualiseren

en dat is het! Open Terminal en voer

python sparse-starter.py

uit om uw spaarzame implementatie van optische stroom te testen. 👏

indien u een code hebt gemist, kunt u de volledige code vinden in sparse-solution.py.

implementatie van dichte optische Flow

we hebben eerder de optische flow berekend voor een schaarse feature set van pixels. Dichte optische flow probeert de optische flow vector te berekenen voor elke pixel van elk frame. Hoewel een dergelijke berekening langzamer kan zijn, geeft het een nauwkeuriger resultaat en een dichter resultaat geschikt voor toepassingen zoals leerstructuur van beweging en video segmentatie. Er zijn verschillende implementaties van dichte optische stroom. We zullen de Farneback methode gebruiken, een van de meest populaire implementaties, met OpenCV, een open source bibliotheek van computer vision algoritmen, voor implementatie.

uw omgeving instellen

Als u dit nog niet hebt gedaan, volg dan Stap 1 van het implementeren van sparse optical flow om uw omgeving in te stellen.

volgende, openen dense-starter.py met je Teksteditor. We zullen alle code in dit Python bestand schrijven.

OpenCV configureren om een video te lezen

Farneback Optical Flow

Gunnar Farneback stelde een effectieve techniek voor om de beweging van interessante functies te schatten door twee opeenvolgende frames te vergelijken in zijn paper Two-Frame Motion Estimation gebaseerd op polynomiale expansie.

ten eerste benadert de methode de vensters (zie Lucas Kanade sectie van sparse optical flow implementatie voor meer details) van beeldframes door kwadratische veeltermen door middel van polynoom expansietransformatietransformatie. Ten tweede, door te observeren hoe de veelterm transformeert onder translation (motion), wordt een methode gedefinieerd om verplaatsingsvelden te schatten uit veelterm expansiecoëfficiënten. Na een reeks verfijningen wordt dichte optische stroom berekend. Farneback ‘ s paper is vrij beknopt en eenvoudig te volgen, dus ik raad ten zeerste aan om door het papier te gaan als u een beter begrip van de wiskundige afleiding wilt.

voor de implementatie van OpenCV berekent het de grootte en richting van de optische stroom uit een 2-kanaals array van stroomvectoren \((dx/dt, dy/dt)\), het optische stroomprobleem. Het visualiseert dan de hoek (richting) van de stroom door tint en de afstand (magnitude) van de stroom door waarde van HSV kleurweergave. De sterkte van HSV is altijd ingesteld op een maximum van 255 voor een optimaal zicht. De documentatie van OpenCV ‘ s implementatie van de Farneback methode via calcOpticalFlowFarneback() kan hier worden gevonden.

visualiseren

en dat is het! Open Terminal en voer

python dense-starter.py

uit om de implementatie van uw dichte optische stroom te testen. 👏

indien u een code hebt gemist, kunt u de volledige code vinden in dense-solution.py.

optische Flow met behulp van Deep Learning

hoewel het probleem van optische flow historisch gezien een optimalisatieprobleem is geweest, hebben recente benaderingen door toepassing van deep learning indrukwekkende resultaten opgeleverd. In het algemeen nemen dergelijke benaderingen twee videoframes als input om de optische stroom (kleurgecodeerde afbeelding) uit te voeren, die kan worden uitgedrukt als:

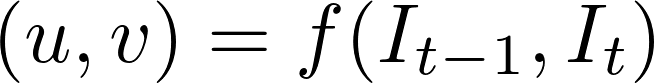
waarbij \(u\) de beweging in de \(x\) richting is, \(v\) de beweging in de \(y\) richting, en \(f\) een neuraal netwerk is dat twee opeenvolgende frames \(I_{T-1}\) (frame op tijd = \(t-1)\) en \(I_t\) (frame op tijd = \(T)\) als input.

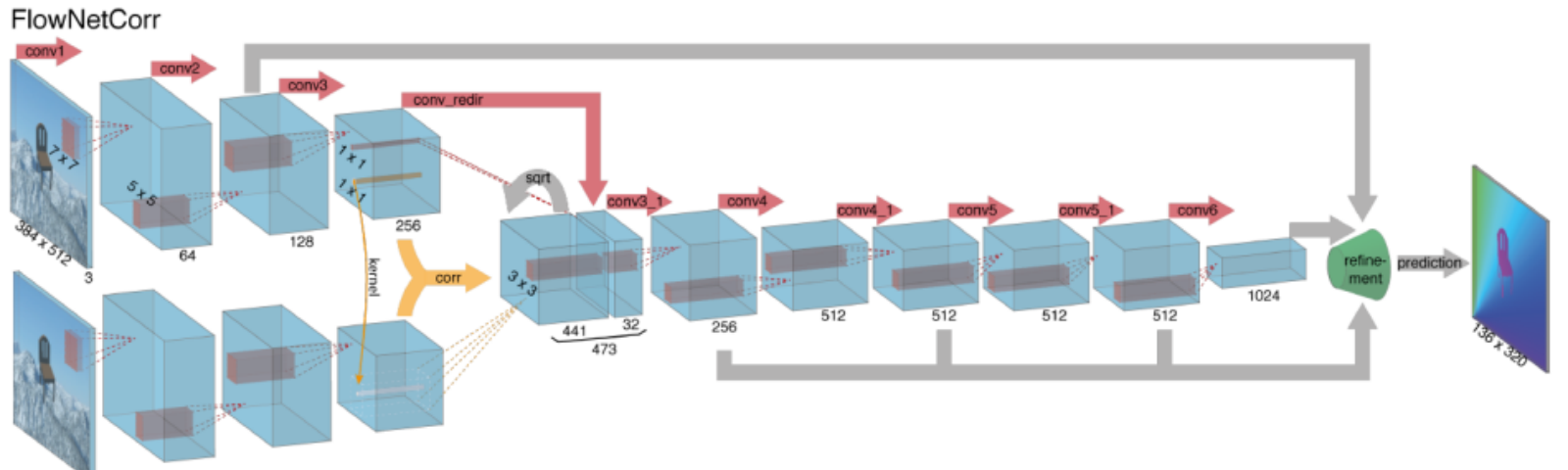
Het berekenen van optische flow met diepe neurale netwerken vereist grote hoeveelheden trainingsgegevens die bijzonder moeilijk te verkrijgen zijn. Dit komt omdat het etiketteren van videobeelden voor optische flow het nauwkeurig uitzoeken van de exacte beweging van elk punt van een afbeelding tot subpixel nauwkeurigheid vereist. Om het probleem van het etiketteren van trainingsgegevens aan te pakken, gebruikten onderzoekers computergraphics om enorme realistische werelden te simuleren. Omdat de werelden worden gegenereerd door instructie, is de beweging van elk punt van een beeld in een video-reeks bekend. Enkele voorbeelden van dergelijke omvatten MPI-Sintel, een open-source CGI-film met optische flow-etikettering weergegeven voor verschillende sequenties, en vliegende stoelen, een dataset van vele stoelen vliegen over Willekeurige achtergronden ook met optische flow-etikettering.

het oplossen van optische stroomproblemen met deep learning is momenteel een zeer hot topic, met varianten van FlowNet, SPyNet, PWC-Net en meer die elk beter presteren dan elkaar op verschillende benchmarks.

Optische Stroomtoepassing: semantische segmentatie

het optische stroomveld is een uitgebreide informatiebron voor de waargenomen scène. Aangezien de technieken van het nauwkeurig bepalen van optische stroom verbeteren, is het interessant om toepassingen van optische stroom in verbinding met verscheidene andere fundamentele computervisies taken te zien. De taak van semantische segmentatie is bijvoorbeeld om een afbeelding te verdelen in reeksen regio ‘ s die overeenkomen met unieke objectklassen, maar dicht geplaatste objecten met identieke texturen zijn vaak moeilijk voor single frame segmentatietechnieken. Als de objecten afzonderlijk worden geplaatst, kunnen de afzonderlijke bewegingen van de objecten echter zeer nuttig zijn wanneer discontinuïteit in het dichte optische stroomveld overeenkomt met grenzen tussen objecten.

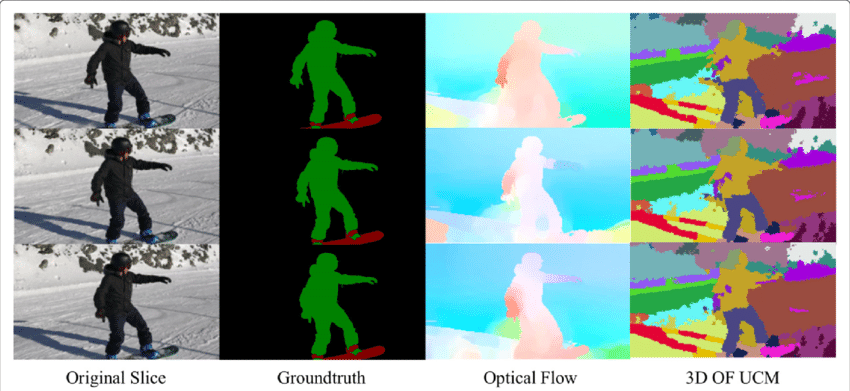
Optische Stroomtoepassing: objectdetectie & Tracking

een andere veelbelovende toepassing van optische stroom kan zijn met objectdetectie en tracking of, in een vorm van hoog niveau, met het bouwen van real-time systemen voor het volgen en analyseren van voertuigen en verkeer. Aangezien sparse optical flow gebruik maakt van het volgen van punten van belang, kunnen dergelijke real-time systemen worden uitgevoerd door feature-based optische flow technieken van ofwel van een stationaire camera of camera ‘ s bevestigd aan voertuigen.

conclusie

fundamenteel functioneren optische stroomvectoren als input voor een groot aantal taken op hoger niveau die inzicht in videosequenties vereisen, terwijl deze taken verder kunnen fungeren als bouwstenen voor nog complexere systemen zoals analyse van gezichtsuitdrukkingen, autonome voertuignavigatie en nog veel meer. Nieuwe toepassingen voor optische stroom die nog ontdekt moeten worden, worden alleen beperkt door de vindingrijkheid van de ontwerpers.

Lazy to code, wilt u niet uitgeven aan GPU ‘ s? Ga naar Nanonets en bouw gratis computer vision modellen!