Inzicht in Deep Residual Networks

Deep residual networks (ResNet) nam de deep learning wereld door storm toen Microsoft Research bracht Deep Residual Learning voor beeldherkenning. Deze netwerken leidden tot de eerste plaats winnende inzendingen in alle vijf de belangrijkste tracks van de ImageNet en COCO 2015 wedstrijden, die beeldclassificatie, objectdetectie en semantische segmentatie behandeld. De robuustheid van ResNets is sindsdien bewezen door verschillende visuele herkenningstaken en door niet-visuele taken met betrekking tot spraak en taal. Ik heb ook ResNet gebruikt naast andere deep learning modellen in mijn promotieonderzoek.

deze post zal een samenvatting geven van de drie papers hieronder, die allemaal zijn geschreven of co-geschreven door ResNet ‘ s uitvinder Kaiming He, omdat ik geloof dat de originele papers de meest intuïtieve en gedetailleerde uitleg geven van het model/netwerken. Hopelijk, dit bericht kan u helpen een beter begrip van de essentie van resterende netwerken te krijgen.

• Deep Residual Learning for Image Recognition
• Identity mappings in Deep Residual Networks
• geaggregeerde residuele transformatie voor Deep Neural Networks

Intuition on Deep Residual Network (stackoverflow ref)

een restblok wordt als volgt weergegeven:

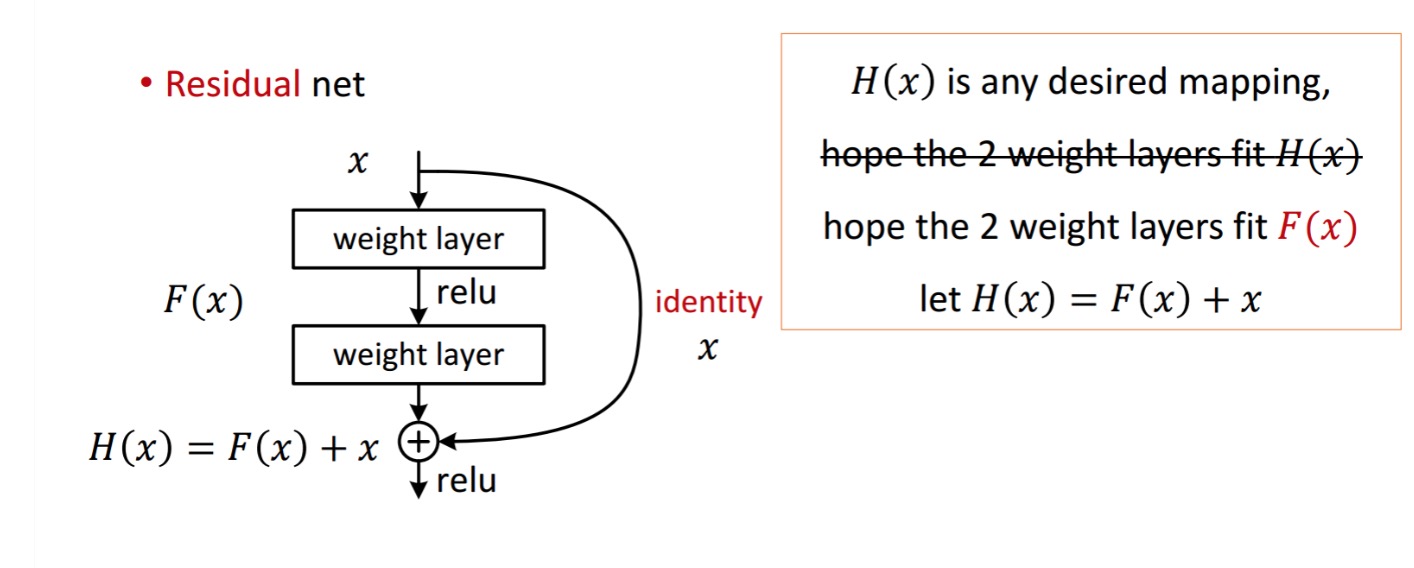
So the De getoonde resteenheid verkrijgt door verwerking met twee gewichtslagen. Dan draagt het bij aan te verkrijgen . Nu, veronderstel dat is uw ideaal voorspelde output die overeenkomt met uw grond waarheid. Sinds, het verkrijgen van de gewenste hangt af van het krijgen van de perfecte . Dat betekent dat de twee gewichtslagen in de resteenheid eigenlijk in staat moeten zijn om het gewenste te produceren , dan is het verkrijgen van het ideale gegarandeerd.

wordt verkregen uit:

wordt verkregen uit:

De auteurs veronderstellen dat de residuele mapping (d.w.z. ) gemakkelijker te optimaliseren is dan . Om te illustreren met een eenvoudig voorbeeld, veronderstellen dat het ideaal . Dan voor een directe mapping zou het moeilijk zijn om een identiteit mapping leren als er een stapel van niet-lineaire lagen als volgt.

dus, het benaderen van de identiteit mapping met al deze gewichten en ReLUs in het midden zou moeilijk zijn.

als we nu de gewenste toewijzing definiëren, dan hebben we alleen maar get als volgt nodig.

het bereiken van het bovenstaande is eenvoudig. Stel gewoon een gewicht op nul en je krijgt een nul output. Voeg terug en je krijgt de gewenste mapping.

Deep Rest Learning for Image Recognition

probleem

wanneer diepere netwerken beginnen te convergeren, is een degradatieprobleem aan het licht gekomen: met een toenemende netwerkdiepte raakt de nauwkeurigheid verzadigd en degradeert snel.

zien hoe degraderen in Actie:

laten we een ondiep netwerk en zijn diepere tegenhanger nemen door er meer lagen aan toe te voegen.

Worst case scenario: de vroege lagen van het dieper model kunnen worden vervangen door ondiep netwerk en de resterende lagen kunnen gewoon fungeren als een identiteitsfunctie (Input gelijk aan output).

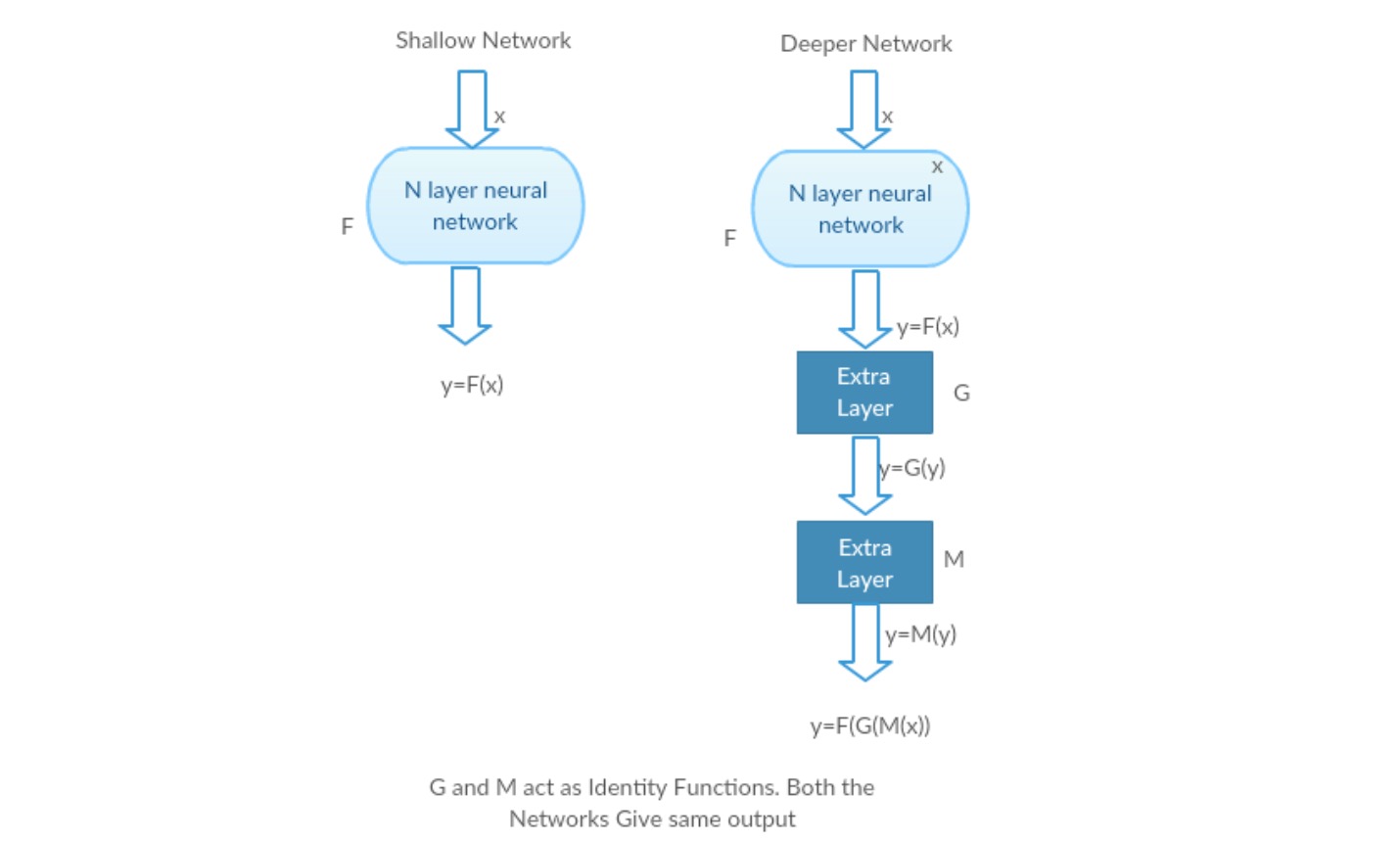
belonend scenario: in het diepere netwerk benaderen de extra lagen de toewijzing beter dan het ondiepere teller deel en vermindert de fout met een significante marge.

Experiment: In het ergste geval moeten zowel het ondiepe netwerk als de diepere variant ervan dezelfde nauwkeurigheid geven. In het belonende scenario zou het diepere model een betere nauwkeurigheid moeten geven dan het ondiepere tegendeel. Maar experimenten met onze huidige oplossers tonen aan dat diepere modellen niet goed presteren. Het gebruik van diepere netwerken vermindert dus de prestaties van het model. Deze papers proberen dit probleem op te lossen met behulp van diepe resterende leerraamwerk.

hoe op te lossen?

in plaats van het leren van een directe toewijzing van met een functie (een paar gestapelde niet-lineaire lagen). Laten we de resterende functie definiëren met behulp van , die kan worden geherframd in, waar en vertegenwoordigt de gestapelde niet-lineaire lagen en de identiteit functie(input=output) respectievelijk.

de hypothese van de auteur is dat het eenvoudig is om de residuele mapping functie te optimaliseren dan om de originele, niet-gerefereerde mapping te optimaliseren .

Intuã tie achter Restblokken:

laten we de Identity mapping als voorbeeld nemen (bijvoorbeeld ). Als de identity mapping optimaal is, kunnen we de reststoffen eenvoudig naar nul () duwen dan om een identity mapping () te passen door een stapel niet-lineaire lagen. In eenvoudige taal is het heel gemakkelijk om te komen met een oplossing als in plaats van het gebruik van stack van niet-lineaire CNN lagen als functie (denk erover na). Dus deze functie is wat de auteurs residuele functie noemden.

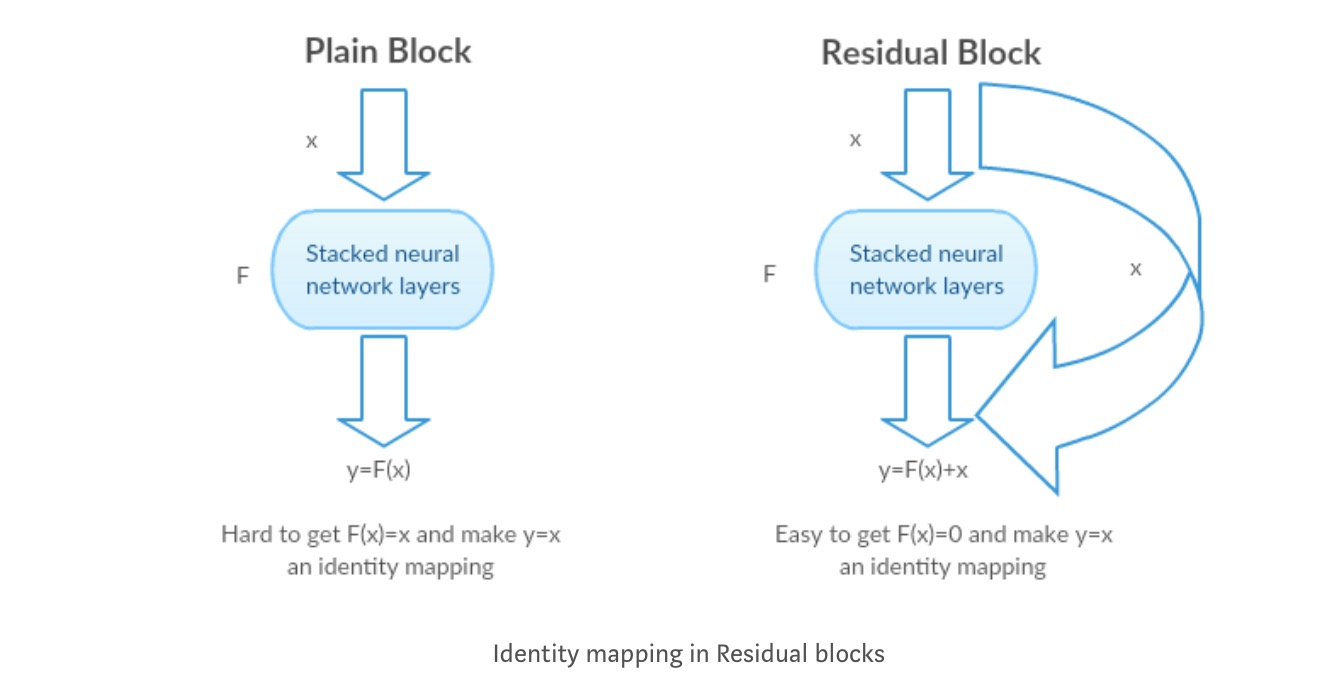
De auteurs deden verschillende tests om hun hypothese te testen. Laten we ze nu bekijken.

testcases:

neem een gewoon netwerk (VGG kind 18 layer network) (Network-1) en een diepere variant daarvan (34-layer, Network-2) en voeg Restlagen toe aan Network-2 (34 laag met restverbindingen, Network-3).

het netwerk ontwerpen:

1. gebruik meestal 3 * 3 filters.
2. Down bemonstering met CNN-lagen met stride 2.
3. globale gemiddelde poolingslaag en een 1000-weg volledig verbonden laag met Softmax op het einde.

Er zijn twee soorten resterende verbindingen:

I. de identity shortcuts () kunnen direct worden gebruikt wanneer de input () en output () van dezelfde afmetingen zijn.

II. wanneer de dimensies veranderen, a) voert de snelkoppeling nog steeds identity mapping uit, met extra nul items opgevuld met de grotere dimensie. B) de projectie sneltoets wordt gebruikt om de dimensie te matchen (gedaan door 1*1 conv) met behulp van de volgende formule

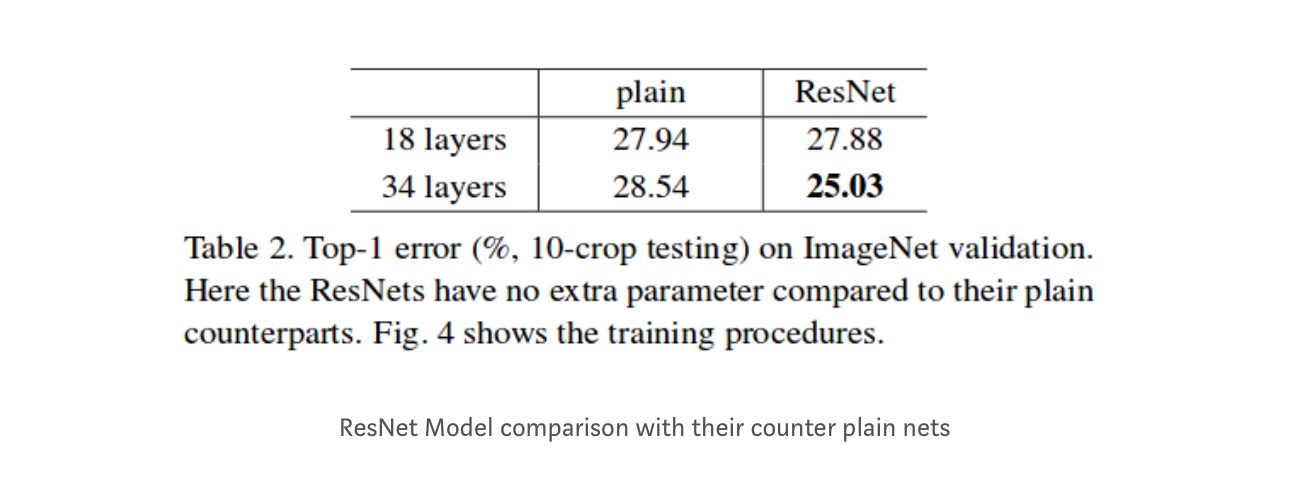
resultaten

hoewel het 18-lagennetwerk slechts de subruimte in 34-lagennetwerk is, presteert het nog steeds beter. ResNet presteert met een aanzienlijke marge beter in het geval het netwerk dieper is

diepere studies

bovendien worden meer netwerken bestudeerd:

elk Resnetblok is ofwel 2 lagen diep (gebruikt in kleine netwerken zoals ResNet 18, 34) of 3 lagen diep( ResNet 50, 101, 152).

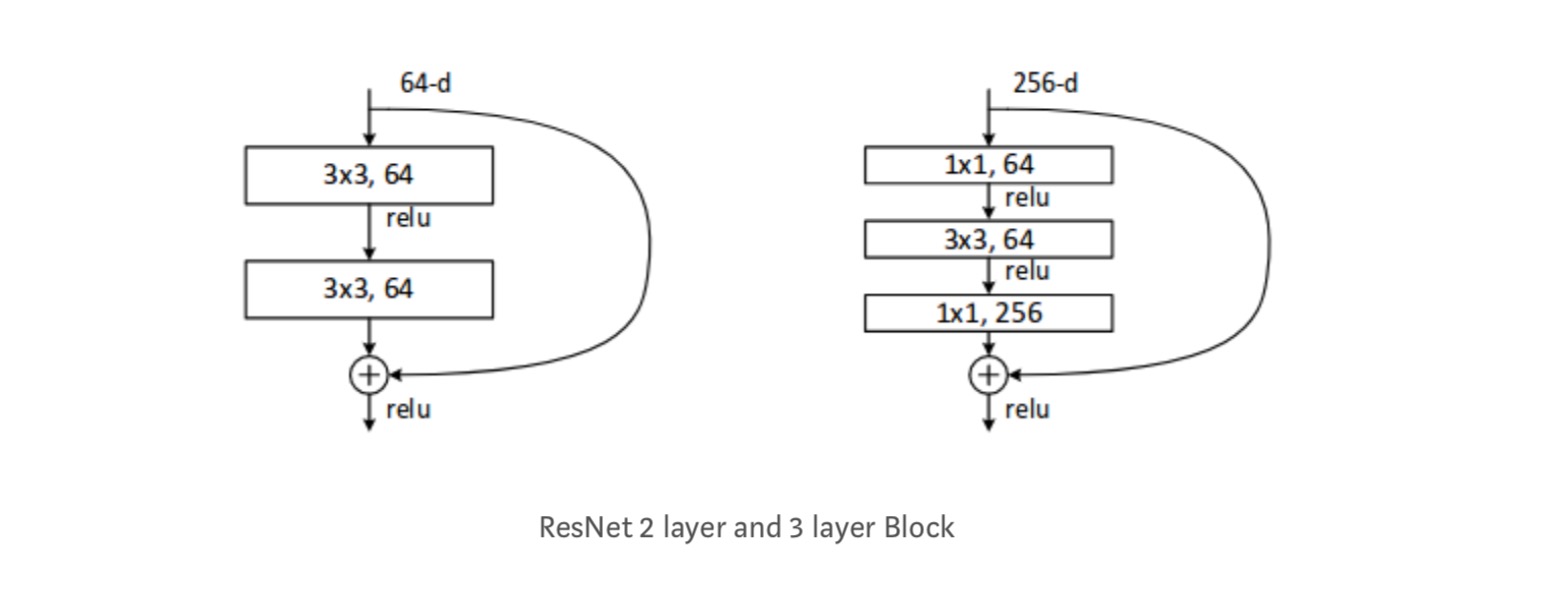
waarnemingen

1. Het ResNet-netwerk convergeert sneller dan het gewone teller-deel ervan.
2. Identity vs Projection shorcuts. Zeer kleine incrementele winsten met behulp van projectie snelkoppelingen (vergelijking-2) in alle lagen. Alle ResNet-blokken gebruiken dus alleen Identity shortcuts met projecties shortcuts die alleen worden gebruikt wanneer de dimensies veranderen.
3. ResNet-34 bereikte een top-5 validatiefout van 5,71% beter dan BN-inception en VGG. ResNet-152 behaalt een top-5 validatiefout van 4,49%. Een ensemble van 6 modellen met verschillende dieptes behaalt een top-5 validatiefout van 3,57%. Het winnen van de 1e plaats in ILSVRC-2015

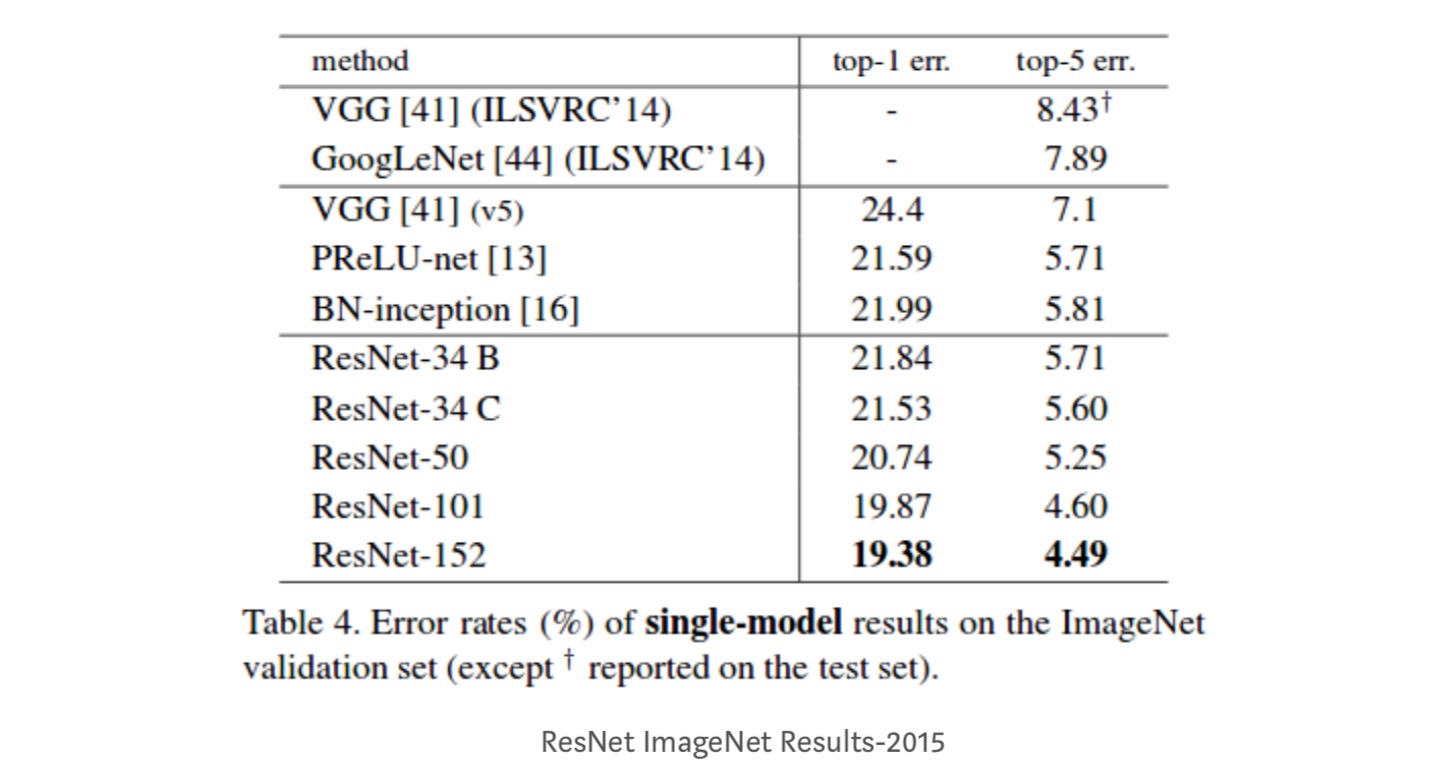
Identity mappings in Deep Residual Networks

Dit artikel geeft het theoretische inzicht waarom verdwijnend gradiëntprobleem niet aanwezig is in Restnetwerken en de rol van skip verbindingen (skip verbindingen betekenen de invoer of ) door Identity mapping (x) te vervangen door verschillende functies.

Inleiding

diepe restnetwerken bestaan uit vele gestapelde “Resteenheden”. Elke eenheid kan worden uitgedrukt in een algemene vorm:

waar en zijn input en output van de eenheid, en is een resterende functie. In de laatste paper, is een identiteit mapping en is een ReLU functie.

het centrale idee van ResNets is het leren van de additieve residuele functie met betrekking tot , met een belangrijke keuze van het gebruik van een identity mapping . Dit wordt gerealiseerd door het aansluiten van een identiteit overslaan verbinding (“snelkoppeling”).

in dit artikel analyseren we diepe restnetwerken door ons te richten op het creëren van een “direct” pad voor het verspreiden van informatie — niet alleen binnen een resteenheid, maar door het hele netwerk. Onze afleidingen laten zien dat als beide en zijn identiteit mappings, het signaal direct kan worden doorgegeven van de ene eenheid naar een andere eenheden, in zowel vooruit als achteruit passen. Onze experimenten laten empirisch zien dat training in het algemeen gemakkelijker wordt als de architectuur dichter bij de bovenstaande twee voorwaarden staat.

om de rol van skip-verbindingen te begrijpen, analyseren en vergelijken we verschillende soorten . We vinden dat de identiteit mapping gekozen in de laatste paper zorgt voor de snelste foutreductie en het laagste trainingsverlies van alle varianten die we onderzocht, terwijl overslaan verbindingen van scaling, gating , en 1×1 kronkels leiden tot een hogere training verlies en fouten. Deze experimenten suggereren dat het houden van een “schoon” informatiepad nuttig is voor het vergemakkelijken van optimalisatie.

om een identity mapping te construeren, zien we de activeringsfuncties (ReLU en BN) als “pre-activering” van de gewichtlagen, in tegenstelling tot de conventionele wijsheid van “post-activering”. Dit standpunt leidt tot een nieuwe resteenheid ontwerp, weergegeven in de volgende figuur. Op basis van deze eenheid presenteren we concurrerende resultaten op CIFAR-10/100 met een 1001-laag ResNet, dat veel gemakkelijker te trainen is en beter generaliseert dan het originele ResNet. Verder rapporteren we verbeterde resultaten op ImageNet met behulp van een 200-laag ResNet, waarvoor de tegenhanger van het laatste papier begint te overfit. Deze resultaten suggereren dat er veel ruimte is om de dimensie van netwerkdiepte te benutten, een sleutel tot het succes van modern deep learning.

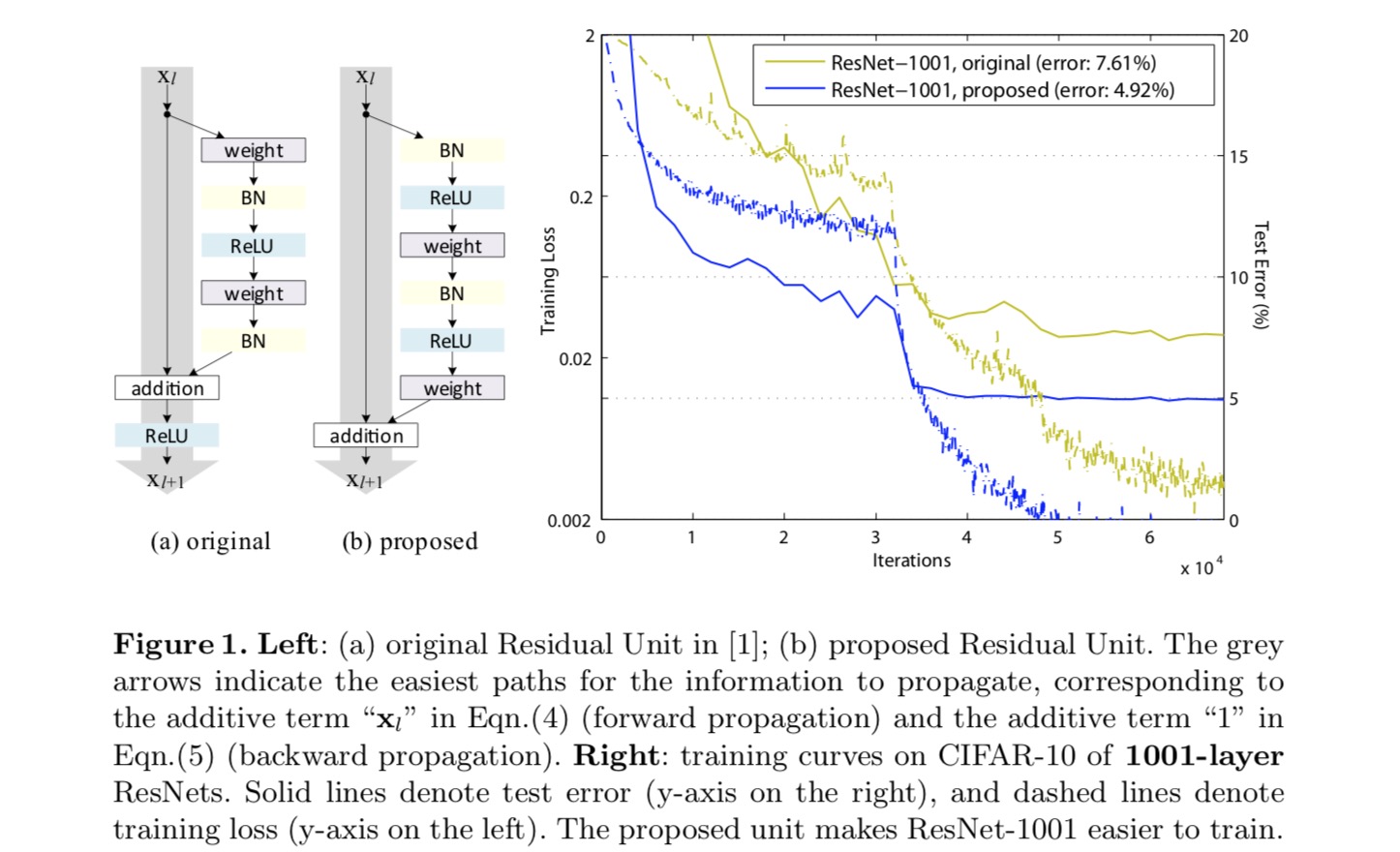
analyse van diepe Restnetwerken

De ResNets die in het laatste artikel zijn ontwikkeld, zijn modularized architecturen die bouwstenen van dezelfde verbindende vorm stapelen. In dit artikel noemen we deze blokken “Resteenheden”. De oorspronkelijke Resteenheid in het laatste papier voert de volgende berekening uit:

Hier is de invoerfunctie voor de-de Resteenheid. is een set van gewichten ( en vooroordelen) geassocieerd met de-de resterende eenheid, en is het aantal lagen in een resterende eenheid (is 2 of 3 in het laatste papier). geeft de resterende functie aan, e.g., een stapel van twee 3×3 convolutionele lagen in het laatste papier. De functie is de operatie na element-wise toevoeging, en in het laatste papier is ReLU. De functie is ingesteld als een identity mapping: .

als het ook een identity mapping is, kunnen we:

recursief verkrijgen we zullen:

hebben voor elke diepere eenheid en elke ondiepere eenheid . Deze vergelijking vertoont een aantal mooie eigenschappen. (1) het kenmerk van een diepere eenheid kan worden weergegeven als het kenmerk van een ondiepere eenheid plus een resterende functie in een vorm van , wat aangeeft dat het model is in een resterende manier tussen alle eenheden en . (2) de eigenschap , van om het even welke diepe eenheid , is de optelling van de outputs van alle voorafgaande resterende functies (plus). Dit in tegenstelling tot een” gewoon netwerk ” waar een functie is een reeks van matrix-Vector producten, laten we zeggen, (het negeren van BN En ReLU).

De Bovenstaande vergelijking leidt ook tot mooie achterwaartse propagatie-eigenschappen. Die de verliesfunctie aangeeft als, uit de kettingregel van de backpropagatie hebben we:

De Bovenstaande vergelijking geeft aan dat de gradiënt kan worden ontleed in twee additieve termen: een term daarvan verspreidt informatie direct zonder betrekking te hebben op gewichtslagen, en een andere term daarvan verspreidt zich door de gewichtslagen. De additieve term of zorgt ervoor dat de informatie direct wordt doorgegeven aan een ondiepere eenheid l. De Bovenstaande vergelijking suggereert ook dat het onwaarschijnlijk is dat de gradiënt wordt geannuleerd voor een mini-batch, omdat in het algemeen de term niet altijd -1 kan zijn voor alle monsters in een mini-batch. Dit houdt in dat de gradiënt van een laag niet verdwijnt, zelfs wanneer de gewichten willekeurig klein zijn.

de bovenstaande twee vergelijkingen suggereren dat het signaal direct kan worden doorgegeven van elke eenheid naar een andere, zowel vooruit als achteruit. De basis van de eerste bovenstaande twee vergelijkingen is twee identity mappings: (1) de identity skip verbinding , en (2) de voorwaarde dat een identity mapping.

belang van identity skip verbindingen

laten we een eenvoudige wijziging overwegen, , om de Identity shortcut te breken:

waar een modulerende scalar is (voor de eenvoud nemen we nog steeds aan dat het identiteit is). Recursief toepassen van deze formulering krijgen we een vergelijking vergelijkbaar met de bovenstaande:

waarbij de notatie de scalaren absorbeert in de resterende functies. Op dezelfde manier hebben we backpropagatie van de volgende vorm:

In tegenstelling tot de vorige vergelijking wordt in deze vergelijking de eerste additieve term gemoduleerd door een factor . Voor een extreem diep netwerk (is groot), als voor allen , kan deze factor exponentieel groot zijn; als voor allen, kan deze factor exponentieel klein zijn en verdwijnen, wat het backpropagated signaal van de snelkoppeling blokkeert en dwingt om door de gewichtlagen te stromen. Dit resulteert in optimalisatie moeilijkheden zoals we laten zien door experimenten.

in de bovenstaande analyse wordt de oorspronkelijke identity skip-verbinding vervangen door een eenvoudige schaling . Als de skip-verbinding meer gecompliceerde transformaties (zoals gating en 1×1 convoluties) vertegenwoordigt, wordt in de bovenstaande vergelijking de eerste term waar de afgeleide van is . Dit product kan ook de verspreiding van informatie belemmeren en de trainingsprocedure belemmeren, zoals blijkt uit de volgende experimenten.

experimenten met Skip verbindingen

we experimenteren met het 110-laags ResNet op CIFAR-10. Deze extreem diepe ResNet-110 heeft 54 twee-laags residuele eenheden (bestaande uit 3×3 convolutionele lagen) en is uitdagend voor optimalisatie. Verschillende soorten skip verbindingen worden geëxperimenteerd. Zie de volgende afbeelding:

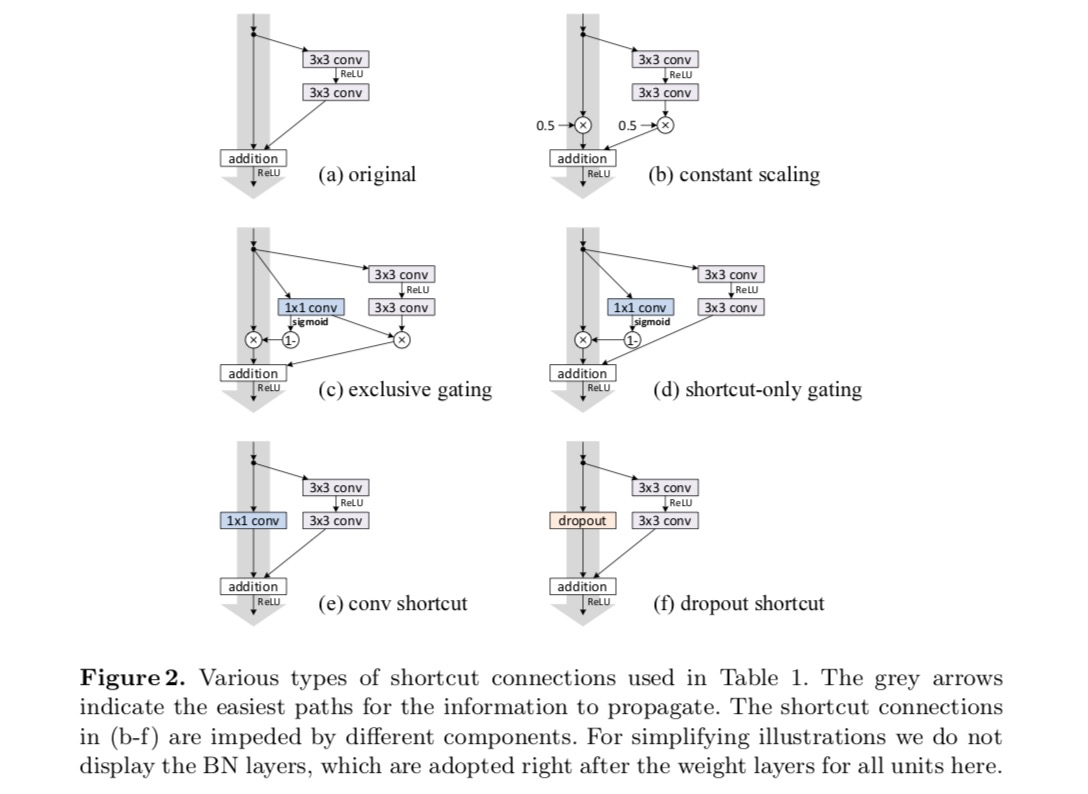
De classificatieresultaten worden weergegeven in de volgende tabel:

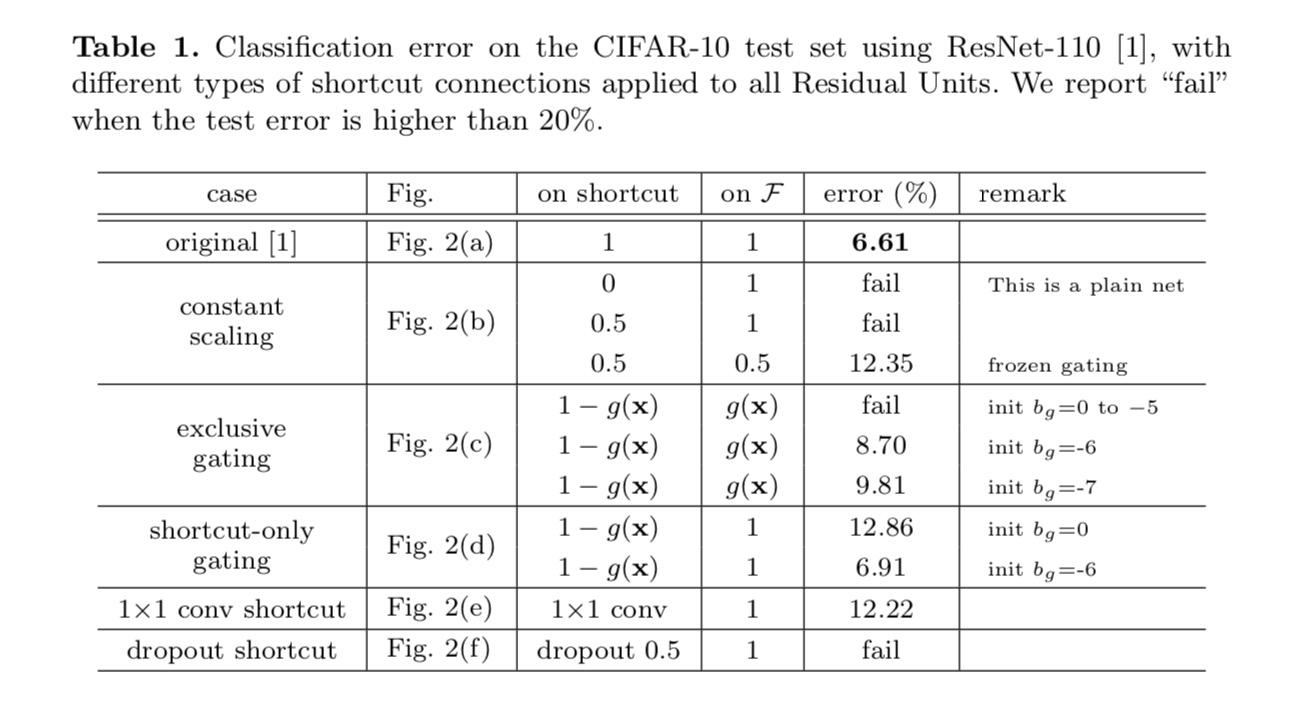
zoals aangegeven door de grijze pijlen in de bovenstaande afbeelding, zijn de snelkoppelingen de meest directe paden voor de informatie om te verspreiden. Multiplicatieve manipulaties (schalen, gating, 1×1 kronkels, en dropout) op de snelkoppelingen kunnen informatie propagatie belemmeren en leiden tot optimalisatie problemen.

Het is opmerkelijk dat de gating en 1×1 convolutionele snelkoppelingen meer parameters introduceren, en sterkere representationele vaardigheden moeten hebben dan identiteits snelkoppelingen. In feite, de shortcut-only gating en 1×1 convolution dekken de oplossing ruimte van identity shortcuts (dat wil zeggen, ze kunnen worden geoptimaliseerd als identity shortcuts). Hun trainingsfout is echter hoger dan die van identity shortcuts, wat aangeeft dat de degradatie van deze modellen wordt veroorzaakt door optimalisatieproblemen, in plaats van representationele vaardigheden.

gebruik van Activeringsfuncties

experimenten in het bovenstaande gedeelte gaan ervan uit dat de activering na toevoeging de identiteitskaarten is. Maar in de bovenstaande experimenten is ReLU zoals ontworpen in de eerste paper. Vervolgens onderzoeken we de impact van .

we willen een identity mapping maken, die wordt gedaan door de activeringsfuncties te herschikken (ReLU en/of BN, batch normalisatie). In de volgende figuur heeft de oorspronkelijke Resteenheid in het laatste papier een vorm in Fig. 4 (a) – BN wordt na elke gewichtslaag gebruikt en ReLU wordt na BN gebruikt, behalve dat de laatste ReLU in een Resteenheid na elementgewijze toevoeging is ( = ReLU). Fig. 4 (b-e) tonen de alternatieven die we hebben onderzocht.

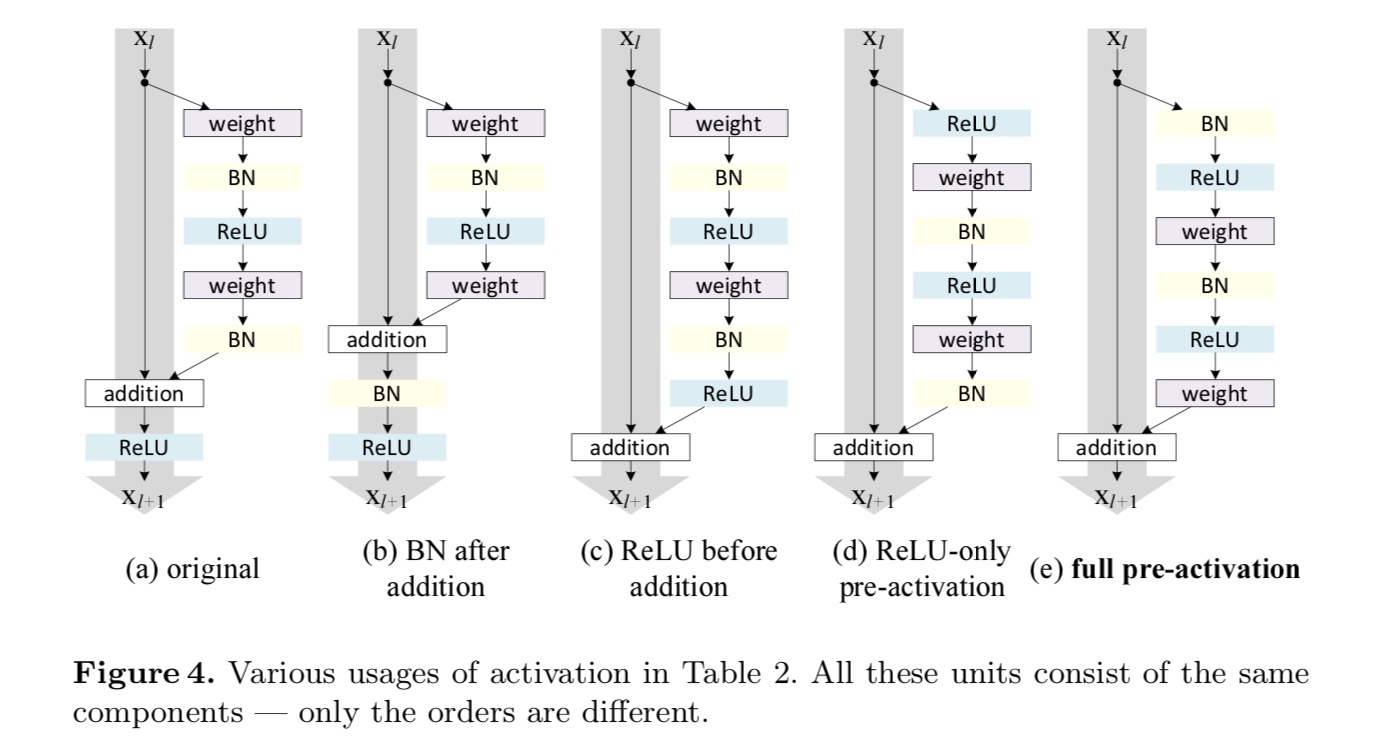
experimenten met activering

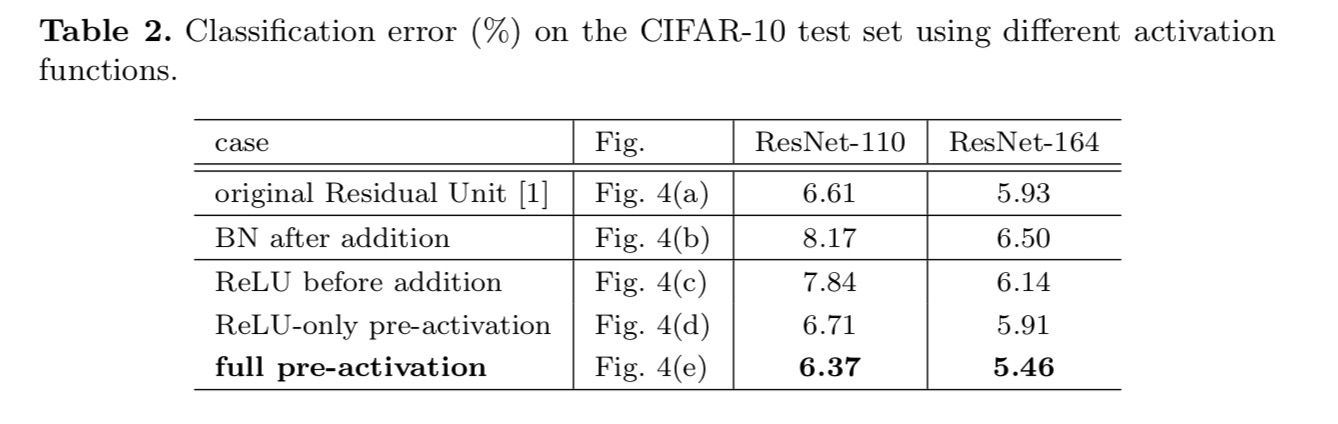
In deze sectie experimenteren we met ResNet-110 en een 164-layer Bottleneck architectuur (aangeduid als ResNet-164). Een bottleneck Resteenheid bestaat uit een 1×1 laag voor het verminderen van dimensie, een 3×3 laag, en een 1×1 laag voor het herstellen van dimensie. Zoals ontworpen in de laatste paper, de computationele complexiteit is vergelijkbaar met de twee-3×3 resterende eenheid.

Post-activering of pre-activering?

in het oorspronkelijke ontwerp beïnvloedt de activering beide paden in de volgende Resteenheid: . Vervolgens ontwikkelen we een asymmetrische vorm waarbij een activering alleen het pad beïnvloedt: , voor elke. Door de notaties te hernoemen, hebben we de volgende vorm:

voor deze nieuwe residuele eenheid zoals in de bovenstaande vergelijking, wordt de nieuwe activering na de toevoeging een identiteitstoewijzing. Dit ontwerp betekent dat als een nieuwe activering na toevoeging asymmetrisch wordt toegepast, deze gelijk staat aan herschikking als de preactivering van de volgende Resteenheid. Dit wordt geïllustreerd in de volgende figuur:

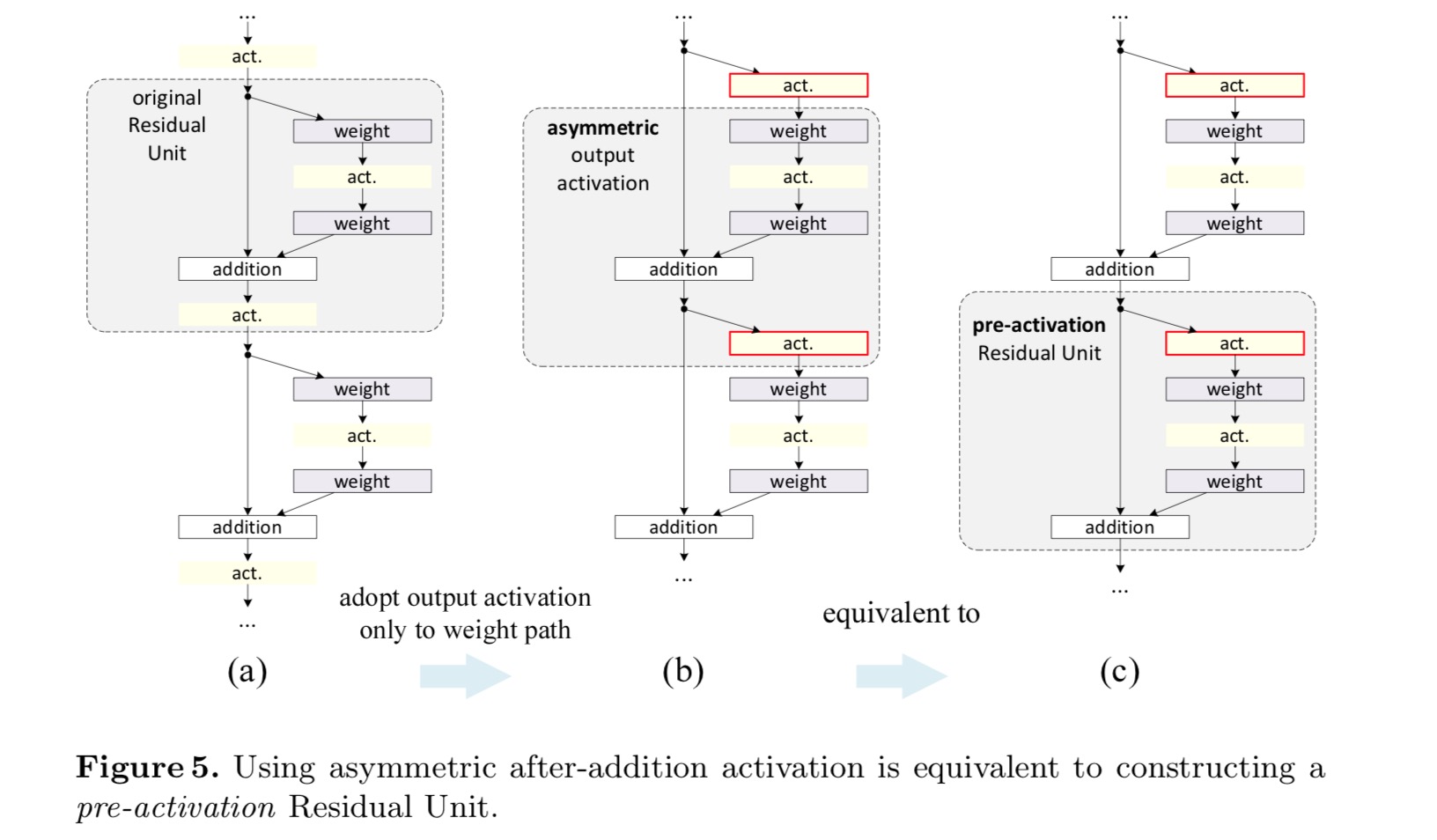
het onderscheid tussen post-activering / pre-activering wordt veroorzaakt door de aanwezigheid van de element-wijze toevoeging. Voor een gewoon netwerk dat N lagen heeft, zijn er n-1 activeringen (BN / ReLU), en het maakt niet uit of we ze als post – of pre-activeringen beschouwen. Maar voor vertakte lagen samengevoegd door toevoeging, is de positie van activering van belang. De verschillende gebruiksmogelijkheden van activering worden weergegeven in Figuur 4.

we experimenteren met twee van zulke ontwerpen: (1) pre-activering alleen voor ReLU en (2) volledige pre-activering waarbij BN en ReLU beide vóór gewichtslagen worden toegepast. Op een of andere manier verrassend, wanneer BN En ReLU beide worden gebruikt als pre-activering, de resultaten worden verbeterd door gezonde marges

we vinden de impact van pre-activering is tweeledig. Ten eerste wordt de optimalisatie verder vergemakkelijkt (in vergelijking met de baseline ResNet) omdat f een identity mapping is. Ten tweede verbetert het gebruik van BN als pre-activering de regularisatie van de modellen.

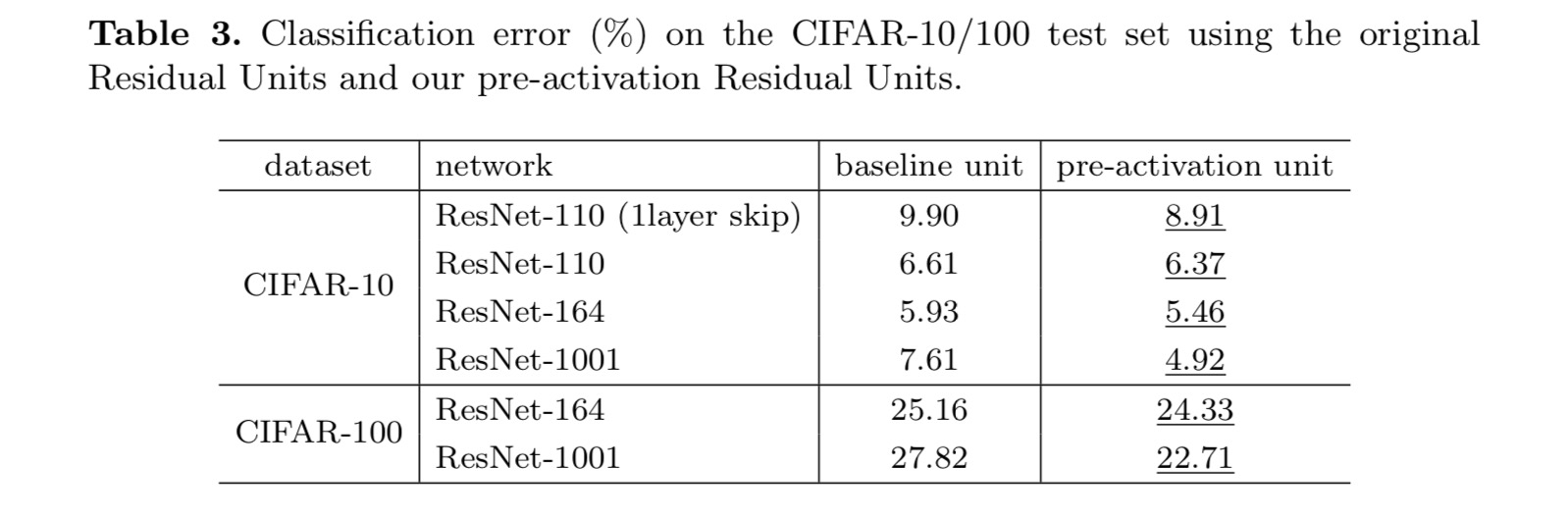
conclusie

Dit Document onderzoekt de voortplantingsformuleringen achter de verbindingsmechanismen van diepe restnetwerken. Onze afleidingen impliceren dat identity short – cut verbindingen en identity after-additie activering essentieel zijn voor het soepel maken van informatieverspreiding. Ablatie-experimenten tonen fenom-ena aan die consistent zijn met onze afleidingen. We presenteren ook 1000-laag diepe netwerken die gemakkelijk kunnen worden getraind en een verbeterde nauwkeurigheid bereiken.

geaggregeerde Resttransformatie voor diepe neurale netwerken

Inleiding

onderzoek naar visuele herkenning ondergaat een overgang van “feature engineering” naar “network engineering”. Menselijke inspanningen zijn verschoven naar het ontwerpen van betere netwerkarchitecturen voor het leren van representaties.

het ontwerpen van architecturen wordt steeds moeilijker met het groeiende aantal hyper-parameters, vooral wanneer er veel lagen zijn. De VGG-netten vertonen een eenvoudige maar effectieve strategie om zeer diepe netwerken te bouwen: het stapelen van bouwstenen van dezelfde vorm. Deze strategie wordt geërfd door ResNets die modules van dezelfde topologie stapelen. Deze eenvoudige regel vermindert de vrije keuzes van hyper parameters, en diepte wordt blootgesteld als een essentiële dimensie in neurale netwerken. Bovendien stellen we dat de eenvoud van deze regel het risico van overmatige aanpassing van de hyperparameters aan een specifieke dataset kan verminderen. De robuustheid van VGG-netten en ResNets is bewezen door verschillende visuele herkenningstaken en door niet-visuele taken met betrekking tot spraak en taal.

In tegenstelling tot VGG-net ‘ s hebben de familie van Inceptiemodellen aangetoond dat zorgvuldig ontworpen topologieën overtuigende nauwkeurigheid kunnen bereiken met een lage theoretische complexiteit. De Beginmodellen zijn in de loop van de tijd geëvolueerd, maar een belangrijke gemeenschappelijke eigenschap is een split-transform-merge strategie. In een Inceptiemodule wordt de input opgesplitst in een paar lagerdimensionale inbeddingen (door 1×1 windingen), getransformeerd door een set gespecialiseerde filters (3×3, 5×5, enz.), en samengevoegd door aaneenschakeling. Het split-transform-merge gedrag van Inceptiemodules zal naar verwachting de representationele kracht van grote en dichte lagen benaderen, maar met een aanzienlijk lagere computationele complexiteit.

ondanks goede nauwkeurigheid is de realisatie van Beginmodellen gepaard gegaan met een reeks complicerende factoren. Hoewel zorgvuldige combinaties van deze componenten uitstekende neurale netwerkrecepten opleveren, is het over het algemeen onduidelijk hoe de Beginselarchitecturen moeten worden aangepast aan nieuwe datasets/taken, vooral wanneer er veel factoren en hyper-parameters moeten worden ontworpen.

in dit artikel presenteren we een eenvoudige architectuur die VGG / ResNets’ strategie van het herhalen van lagen aanneemt, terwijl de split-transform-merge strategie op een eenvoudige, uitbreidbare manier wordt benut. Een module in ons netwerk voert een reeks transformaties uit, elk op een laagdimensionale inbedding, waarvan de output wordt samengevoegd door optelling. We streven naar een eenvoudige realisatie van dit idee — de transformaties die moeten worden samengevoegd zijn allemaal van dezelfde topologie. Dit ontwerp stelt ons in staat om uit te breiden tot een groot aantal transformaties zonder gespecialiseerde ontwerpen.

We tonen empirisch aan dat onze geaggregeerde transformaties beter presteren dan de oorspronkelijke ResNet-module, zelfs onder de beperkte voorwaarde van het handhaven van computationele complexiteit en modelgrootte. We benadrukken dat hoewel het relatief eenvoudig is om de nauwkeurigheid te verhogen door de capaciteit te verhogen (dieper of breder), methoden die de nauwkeurigheid verhogen met behoud (of vermindering) complexiteit zeldzaam zijn in de literatuur.

onze methode geeft aan dat kardinaliteit (de grootte van de reeks transformaties) een concrete, meetbare dimensie is die van centraal belang is, naast de afmetingen van breedte en diepte. Experimenten tonen aan dat toenemende kardinaliteit een effectievere manier is om nauwkeurigheid te verkrijgen dan dieper of breder te gaan, vooral wanneer diepte en breedte afnemende rendementen beginnen te geven voor bestaande modellen.

onze neurale netwerken, genaamd ResNeXt (wat de volgende dimensie suggereert), presteren beter dan ResNet-101/152, ResNet-200, Inception-v3 en Inception-ResNet-v2 op de ImageNet classificatiedataset. Met name een 101-laags ResNeXt is in staat om een betere nauwkeurigheid te bereiken dan ResNet-200, maar heeft slechts 50% complexiteit. Bovendien vertoont ResNeXt aanzienlijk eenvoudiger ontwerpen dan alle Inception-modellen.

methode

we hanteren een sterk gemoduleerd ontwerp na VGG / ResNets. Ons netwerk bestaat uit een stapel restblokken. Deze blokken hebben dezelfde topologie, en zijn onderworpen aan twee eenvoudige regels geïnspireerd door VGG/ResNets: (1) als het produceren van ruimtelijke kaarten van dezelfde grootte, de blokken delen dezelfde hyper-parameters (breedte en filtergrootte), en (2) elke keer als de ruimtelijke kaart wordt gedemonstreerd met een factor 2, wordt de breedte van de blokken vermenigvuldigd met een factor 2. De tweede regel zorgt ervoor dat de computationele complexiteit, in termen van FLOPs (floating-point operaties, in #van multiply-adds), ongeveer hetzelfde is voor alle blokken.

Met deze twee regels hoeven we alleen een template module te ontwerpen, en alle modules in een netwerk kunnen dienovereenkomstig worden bepaald. Deze twee regels beperken de ontwerpruimte sterk en stellen ons in staat om ons te concentreren op een paar belangrijke factoren. De door deze regels geconstrueerde netwerken staan in Tabel 1.

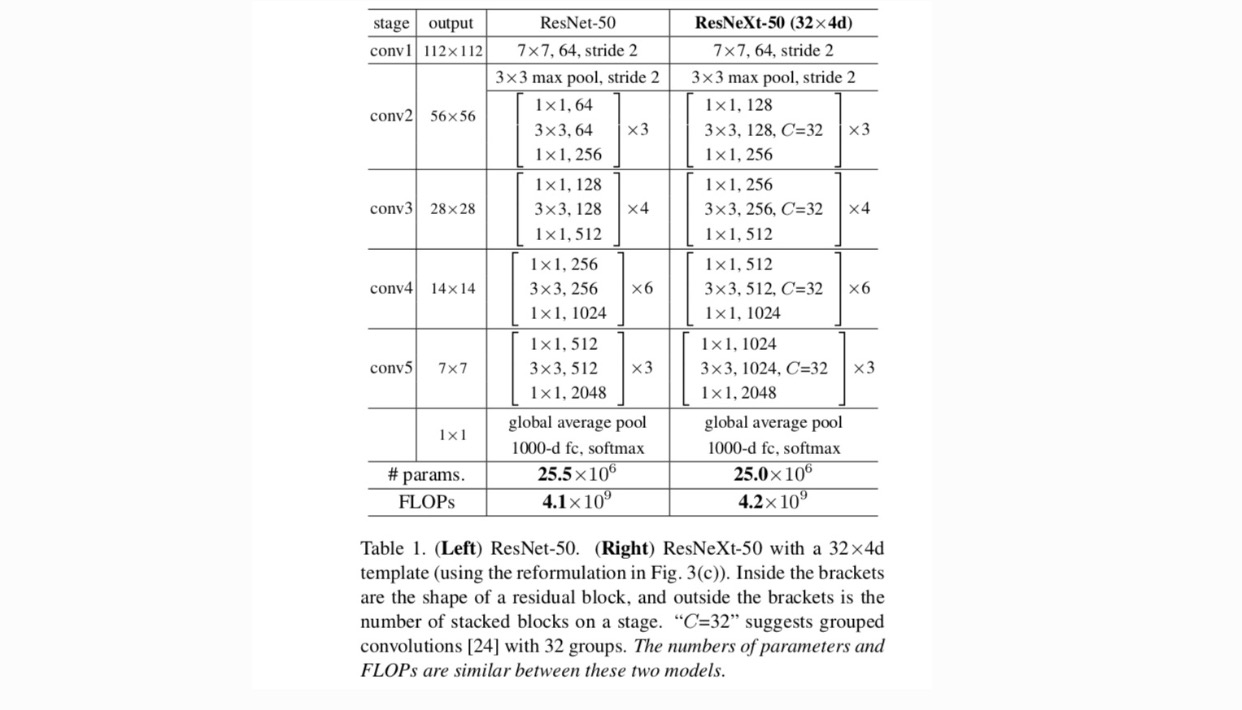
De eenvoudigste neuronen in kunstmatige neurale netwerken voeren innerlijke product (gewogen som), dat is de elementaire transformatie gedaan door volledig verbonden en convolutionele lagen.

bovenstaande bewerking kan worden herschikt als een combinatie van splitsen, transformeren en aggregeren. (1): splitsen: de vector wordt gesneden als een laag-dimensionale inbedding, en in het bovenstaande, het is een single-dimensionale subruimte (2) transformeren: de laag-dimensionale representatie wordt getransformeerd, en in het bovenstaande, het is gewoon geschaald: (3) aggregeren: de transformaties in alle inbeddingen worden geaggregeerd door .

gegeven de bovenstaande analyse van een eenvoudig neuron, overwegen we de elementaire transformatie (w_i, x_i) te vervangen door een meer generieke functie, die op zichzelf ook een netwerk kan zijn. Formeel presenteren we geaggregeerde transformaties als:

waar een willekeurige functie kan zijn. Analoog aan een eenvoudig neuron, moet projecteren in een (optioneel laag-dimensionale) inbedding en dan transformeren.

we verwijzen naar cardinaliteit. is in een positie vergelijkbaar met in, maar hoeft niet gelijk en kan een willekeurig getal zijn. Door experimenten laten we zien dat kardinaliteit een essentiële dimensie is en effectiever kan zijn dan de afmetingen van breedte en diepte.

in dit artikel beschouwen we een eenvoudige manier om de transformatiefuncties te ontwerpen: alle functies hebben dezelfde topologie. Dit breidt de VGG-stijl strategie van het herhalen van lagen van dezelfde vorm. We stellen de individuele transformatie als de bottleneck-vormige architectuur in Fig. 1 (rechts). In dit geval, de eerste 1×1 laag in elke produceert de laag-dimensionale inbedding.

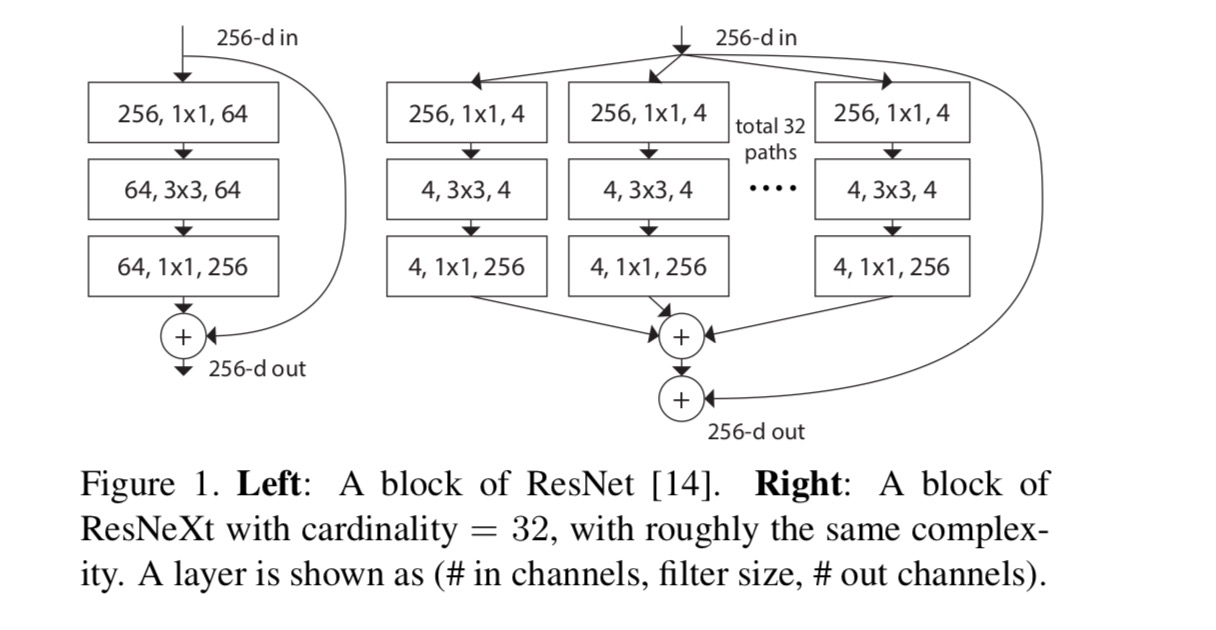
de geaggregeerde transformatie in de laatste vergelijking dient als de residuele functie:

waarbij de output is.

de relaties tussen Resnext en Inception-ResNet / Grouped-Convolutions worden weergegeven in de volgende figuur:

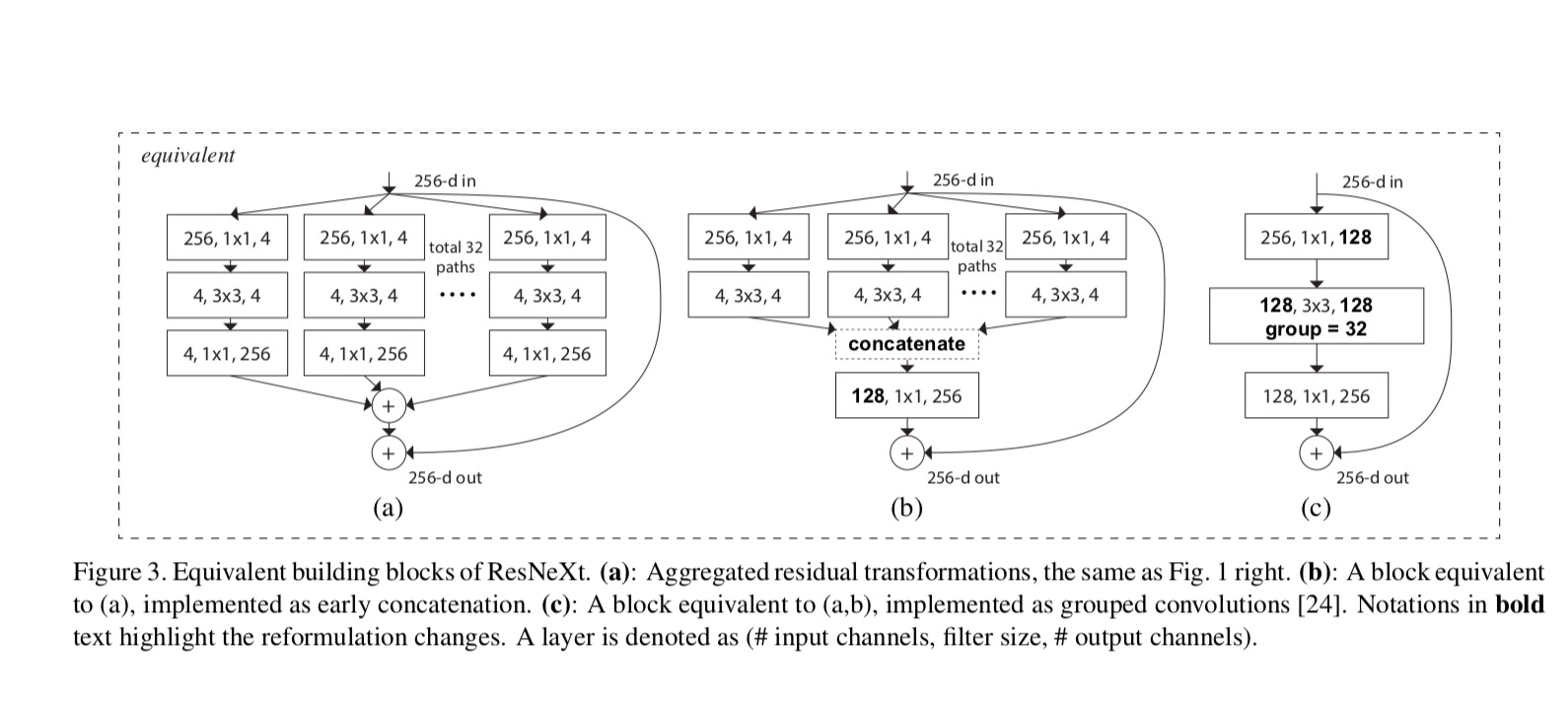
wanneer we verschillende kardinaliteiten evalueren met behoud van complexiteit, willen we de wijziging van andere hyper-parameters minimaliseren. We kiezen ervoor om de breedte van de bottleneck aan te passen (bijvoorbeeld 4-d in Fig.1(rechts)), omdat deze geïsoleerd kan worden van de input en output van het blok. Deze strategie introduceert geen verandering aan andere hyper-parameters (diepte of input/output breedte van blokken), dus is nuttig voor ons om zich te concentreren op de impact van kardinaliteit.

in Fig. 1 (Links), de oorspronkelijke ResNet bottleneck blok heeft parameters en proportionele FLOPs (op dezelfde functie Kaart grootte). Met flessenhals breedte, onze sjabloon in Fig. 1 (rechts) heeft: parameters en proportionele FLOPs. Wanneer en, dit nummer . De volgende tabel toont de relatie tussen kardinaliteit en flessenhals breedte .

experimenten

kardinaliteit vs.breedte. We evalueren eerst de trade-off tussen kardinaliteit en bottleneck breedte, onder behouden complexiteit zoals vermeld in Tabel 2. Tabel 3 geeft de resultaten weer. In vergelijking met ResNet-50 heeft de 32×4d ResNeXt-50 een validatiefout van 22,2%, wat 1,7% lager is dan de 23,9% baseline van het ResNet. Doordat de kardinaliteit toeneemt van 1 naar 32 terwijl de complexiteit wordt behouden, blijft het foutenpercentage afnemen. Bovendien heeft de 32×4d ResNeXt ook een veel lagere trainingsfout dan de ResNet countetpart, wat suggereert dat de voordelen niet afkomstig zijn van regularisatie, maar van sterkere representaties.

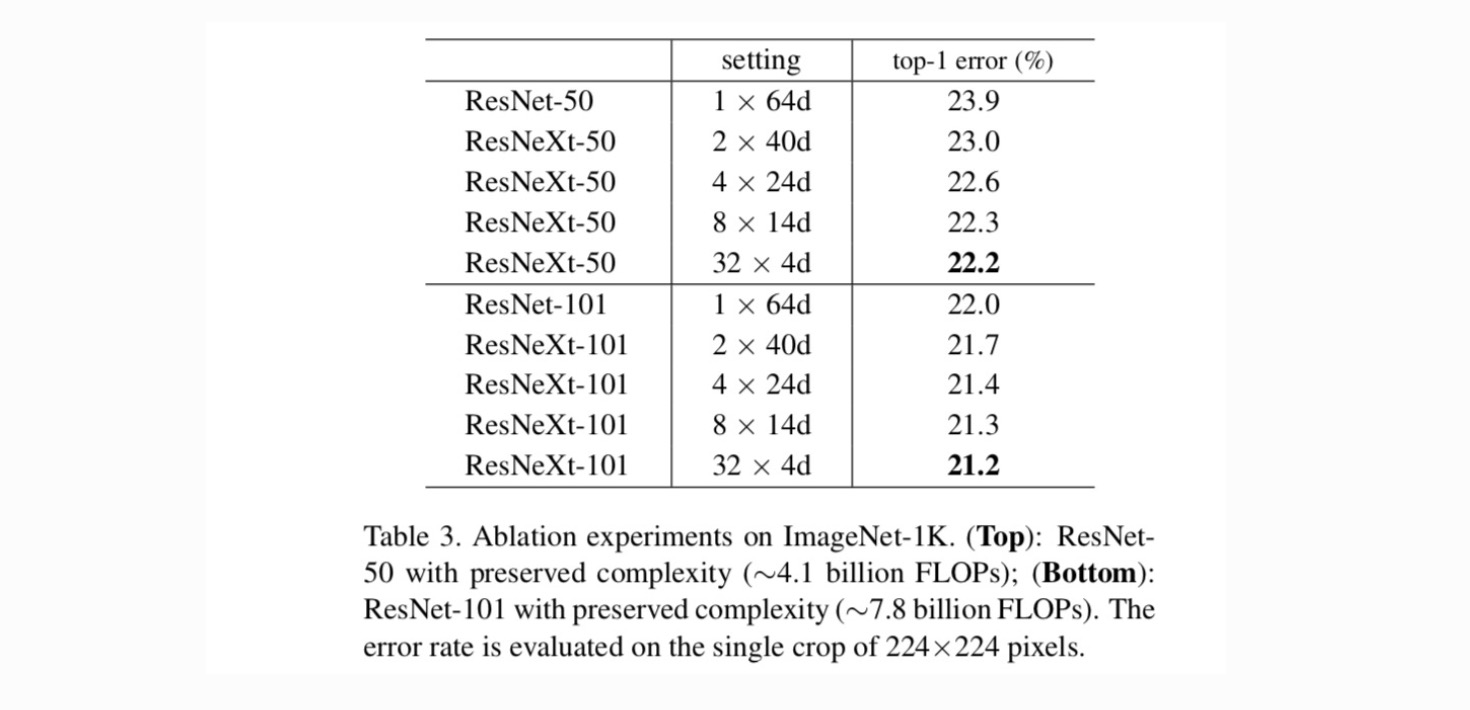
toenemende kardinaliteit vs.dieper / breder.

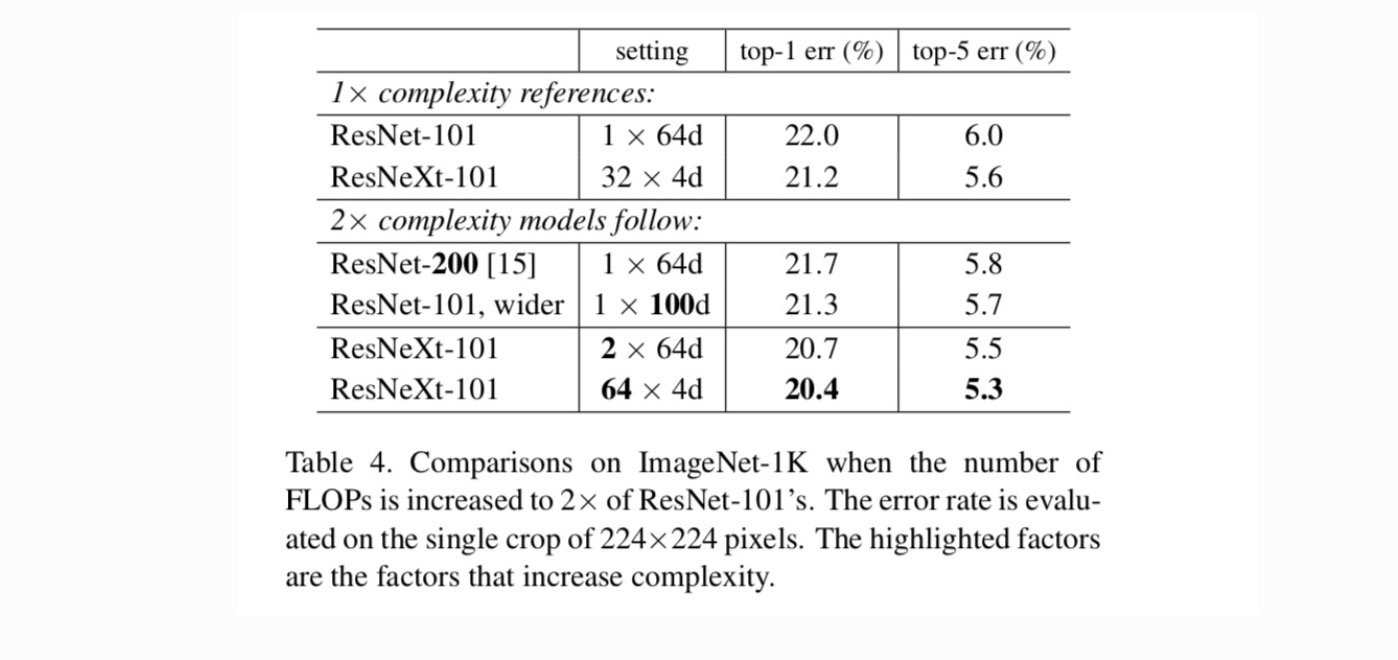
vervolgens onderzoeken we de toenemende complexiteit door cardinaliteit C of diepte of breedte te verhogen. We vergelijken de volgende varianten (1) die dieper gaan naar 200 lagen. We nemen de ResNet-200 aan. (2) breder gaan door het vergroten van de bottleneck breedte. (3) toename van de kardinaliteit door verdubbeling van C.

Tabel 4 toont aan dat een toename van de complexiteit met 2× consistent fouten vermindert ten opzichte van de basislijn van ResNet-101 (22,0%). Maar de verbetering is klein wanneer dieper (ResNet-200, met 0,3%) of breder (bredere ResNet-101, met 0,7%). Integendeel, toenemende kardinaliteit C laat veel betere resultaten zien dan dieper of breder gaan.

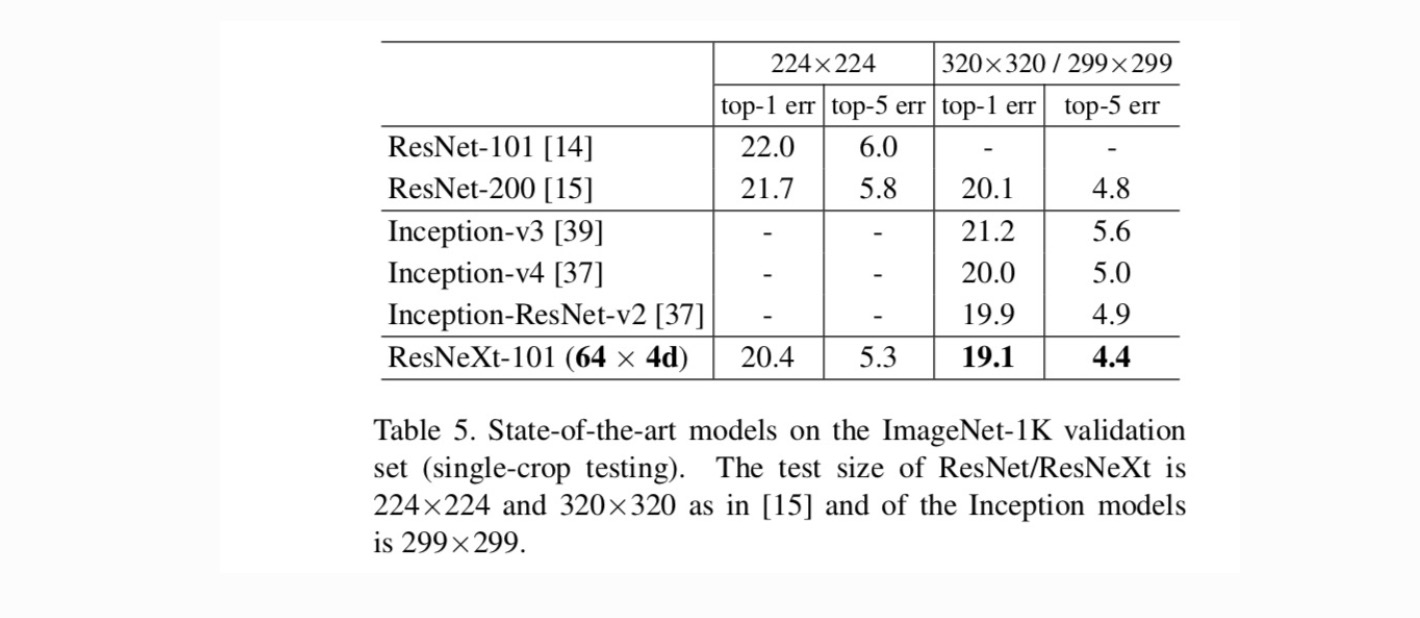
vergelijkingen met state-of-the-art resultaten. Tabel 5 toont meer resultaten van testen met één gewas op de Validatieset ImageNet. Onze resultaten zijn gunstig vergeleken met ResNet, Inception-v3/v4 en Inception-ResNet-v2, waardoor een single-crop top-5 foutenpercentage van 4,4% wordt bereikt. Bovendien is ons architectuurontwerp veel eenvoudiger dan alle Inception-modellen en vereist het aanzienlijk minder hyper-parameters die met de hand moeten worden ingesteld.