unsupervised Bayesian Inference (reducing dimensions and unearthing features)

eindelijk, het moment waarop u allen hebt gewacht, de volgende in onze niet-gecontroleerde Bayesiaanse gevolgtrekking serie: Onze (niet zo) diepe duik in de Sobel Operator.
een echt magisch algoritme voor randdetectie, het maakt low-level functie-extractie en dimensionaliteitsreductie mogelijk, waardoor ruis in de afbeelding wordt verminderd. Het is vooral nuttig geweest in gezichtsherkenning toepassingen.het liefdeskind uit 1968 van Irwin Sobel en Gary Feldman (Stanford Artificial Intelligence Laboratory), dit algoritme was de inspiratie van vele moderne technieken voor randdetectie. Door twee tegengestelde kernels of maskers over een gegeven afbeelding te convolveren (bijv. zie linksonder) (elk in staat om zowel horizontale als verticale randen te detecteren), kunnen we een minder lawaaierige, gladgestreken voorstelling maken (zie rechtsonder).
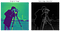
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel waarden (meestal Luminantie) door het verschil tussen elke pixel (de ankerpixel) en de omringende pixels te differentiëren (in wezen de afgeleide van een afbeelding benaderen).
Dit resulteert in het gladmaken van de originele afbeelding en het produceren van een lagere dimensie uitvoer, waar low-level geometrische kenmerken duidelijker kunnen worden gezien. Deze uitgangen kunnen dan worden gebruikt als input in meer complexe classificatie algoritmen, of als voorbeelden gebruikt voor unsupervised probabilistic clustering via Kullback-Leibler Divergence (KLD) (zoals te zien in mijn recente blog op LBP).
het genereren van onze uitvoer met een lagere dimensie vereist dat we de afgeleide van de afbeelding nemen. Eerst berekenen we het derivaat in zowel de x-als y-richtingen. We creëren twee 3×3 kernels (zie matrices), met nullen langs het midden van de corresponderende as, twee in de middenvierkant loodrecht op het centrale nulpunt en enen in elk van de hoeken. Elk van de niet-nulwaarden moet positief zijn boven / rechts van de nullen (afhankelijk van de as) en negatief op hun corresponderende zijde. Deze kernels worden Gx en Gy genoemd.
deze worden weergegeven in het formaat:
Deze kernels zullen dan over onze afbeelding convolveren, waarbij de centrale pixel van elke kernel over elke pixel in de afbeelding wordt geplaatst. We gebruiken matrixvermenigvuldiging om de intensiteitswaarde te berekenen van een nieuwe corresponderende pixel in een uitvoerafbeelding, voor elke kernel. Daarom eindigen we met twee uitvoerbeelden (één voor elke Cartesiaanse richting).
Het doel is om het verschil/verandering te vinden tussen de pixel in de afbeelding en alle pixels in de gradiëntmatrix (kernel) (Gx en Gy). Wiskundig gezien kan dit worden uitgedrukt als.
Side note:
We zijn technisch niet convolving iets. Hoewel we graag verwijzen naar’ convolutions ‘ in AI en machine learning Cirkels, een convolution zou inhouden het omdraaien van de originele afbeelding. Wiskundig gesproken, als we verwijzen naar convoluties, berekenen we echt de correlatie tussen elk 3×3 gebied van de invoer en het masker voor elke pixel. De uitvoerafbeelding is de totale covariantie tussen het masker en de invoer. Zo worden de randen gedetecteerd.
terug naar onze Sobel uitleg…
de berekende waarden voor elke matrixvermenigvuldiging tussen het masker en 3×3 sectie van de invoer worden opgeteld om de uiteindelijke waarde voor de pixel in de uitvoerafbeelding te produceren. Dit genereert een nieuwe afbeelding die informatie bevat over de aanwezigheid van verticale en horizontale randen in de oorspronkelijke afbeelding. Dit is een geometrische weergave van de originele afbeelding. Verder, omdat deze operator gegarandeerd elke keer dezelfde output produceert, zorgt deze techniek voor stabiele randdetectie voor beeldsegmentatietaken.
op basis Van deze resultaten, kunnen we berekenen zowel de omvang en het verloop van de gradiënt richting (met de arctangens (operator) op een gegeven pixel (x,y):
Uit dit kunnen we vaststellen dat de pixels met een grote omvang hebben meer kans om een voorsprong in de afbeelding, terwijl de richting informeert ons over de rand van de oriëntatie (hoewel de richting is niet nodig voor het genereren van onze uitvoer).
een eenvoudige implementatie:
Hier is een eenvoudige implementatie van de Sobel operator in python (met behulp van NumPy) om je een gevoel voor het proces te geven (voor alle beginnende programmeurs die er zijn).
Deze implementatie is een python variant van het Wikipedia pseudocode voorbeeld, met als doel te laten zien hoe je dit algoritme zou kunnen implementeren, terwijl je ook de verschillende stappen in het proces demonstreert.
wat kan ons dat schelen?
hoewel de gradiëntbenadering die door deze operator wordt geproduceerd relatief ruw is, biedt deze een uiterst rekenefficiënte methode voor het berekenen van randen, hoeken en andere geometrische kenmerken van afbeeldingen. Op zijn beurt heeft het de weg geëffend voor een aantal dimensionaliteitsreductie en extractietechnieken, zoals lokale binaire patronen (zie mijn andere blog voor meer details over deze techniek).
Als u uitsluitend op geometrische kenmerken vertrouwt, loopt u het risico belangrijke informatie te verliezen tijdens het coderen van onze gegevens, maar de trade-off is wat een snelle voorbewerking van de gegevens en op zijn beurt een snelle training mogelijk maakt. Daarom is deze techniek vooral nuttig in scenario ‘ s waar textuur en geometrische kenmerken kunnen worden beschouwd als zeer belangrijk bij het definiëren van de input. Daarom kan de gezichtsherkenning met de Sobel-operator met een relatief hoge nauwkeurigheid worden voltooid. Deze techniek is echter misschien niet de beste keuze als men probeert inputs te classificeren of te groeperen die kleur als hun belangrijkste onderscheidende factor gebruiken.
deze methode is nog steeds zeer effectief voor het verkrijgen van een laag-dimensionale representatie van geometrische kenmerken en een uitstekend uitgangspunt voor dimensionaliteit en ruisonderdrukking, voorafgaand aan het gebruik van andere classifiers of voor gebruik in Bayesiaanse inferentiemethodologieën.