Inleiding
Principal Components Analysis (PCA) is een dimensionaliteitsreductiealgoritme dat kan worden gebruikt om uw unsupervised feature learning algoritme aanzienlijk te versnellen. Nog belangrijker, het begrijpen van PCA zal ons in staat stellen om later whitening implementeren, dat is een belangrijke pre-processing stap voor veel algoritmen.
stel dat u uw algoritme traint op afbeeldingen. Dan zal de invoer enigszins redundant zijn, omdat de waarden van aangrenzende pixels in een afbeelding sterk gecorreleerd zijn. Concreet, stel dat we trainen op 16×16 grijswaarden image patches. Dan zijn\textstyle x \in \ re^{256} 256 dimensionale vectoren, met één eigenschap \textstyle x_j die overeenkomt met de intensiteit van elke pixel. Vanwege de correlatie tussen aangrenzende pixels, zal PCA ons in staat stellen om de invoer te benaderen met een veel lagere dimensionale, terwijl er zeer weinig fout optreedt.
voorbeeld en wiskundige achtergrond
voor ons lopende voorbeeld gebruiken we een dataset \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} met \textstyle n=2 dimensionale inputs, zodat \textstyle x^{(i)} \in \Re^2. Stel dat we de gegevens willen reduceren van 2 dimensies naar 1. (In de praktijk willen we misschien gegevens verminderen van 256 naar 50 dimensies, bijvoorbeeld; maar met behulp van lagere dimensionale gegevens in ons voorbeeld stelt ons in staat om de algoritmen beter te visualiseren.) Hier is onze dataset:
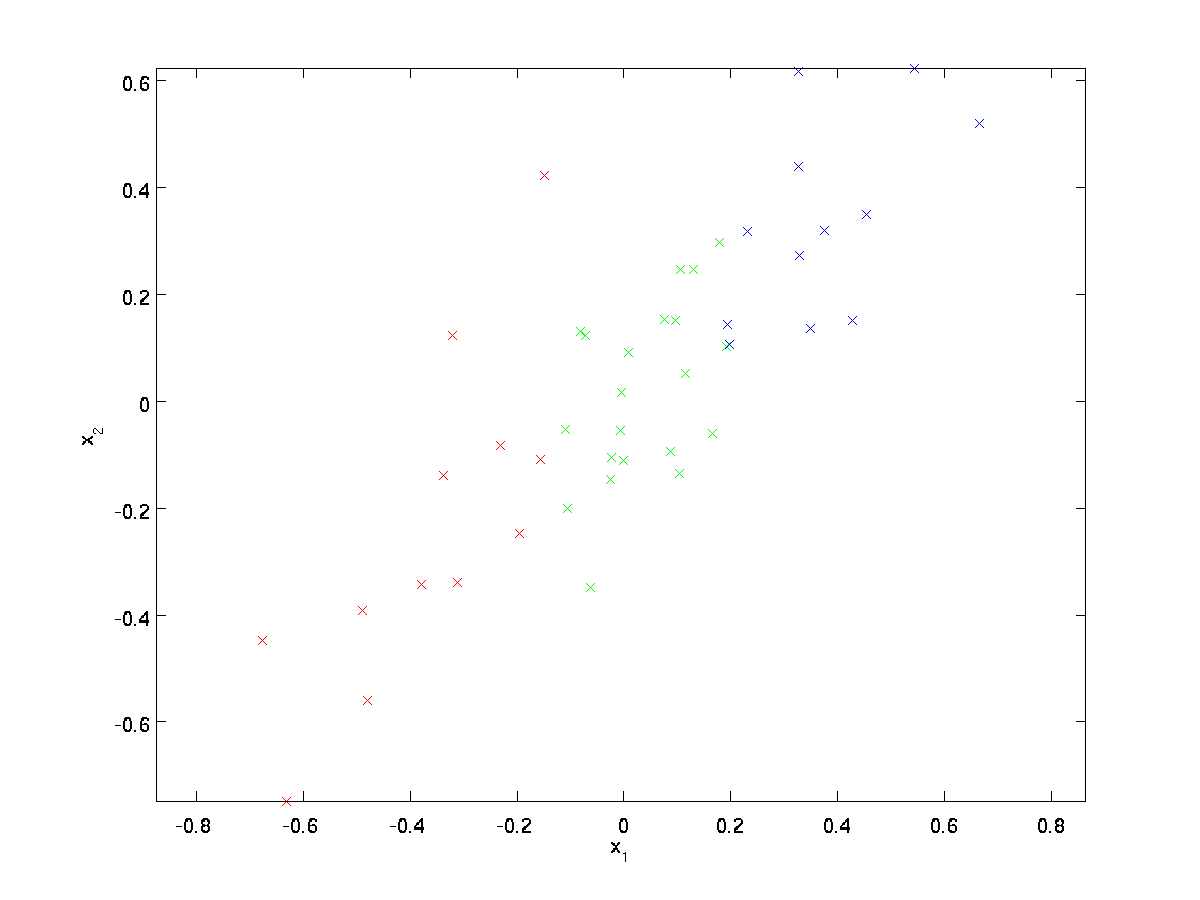
deze gegevens zijn al vooraf verwerkt zodat elk van de eigenschappen \textstyle x_1 en \textstyle x_2 ongeveer hetzelfde gemiddelde (nul) en variantie hebben.
ter illustratie hebben we elk van de punten ook een van de drie kleuren ingekleurd, afhankelijk van hun \ textstyle x_1 waarde; deze kleuren worden niet gebruikt door het algoritme, en zijn alleen ter illustratie.
PCA zal een lagere-dimensionale subruimte vinden waarop onze gegevens kunnen worden geprojecteerd.
uit visueel onderzoek van de gegevens blijkt dat \ textstyle u_1 de belangrijkste variatierichting van de gegevens is, en \textstyle u_2 de secundaire variatierichting:
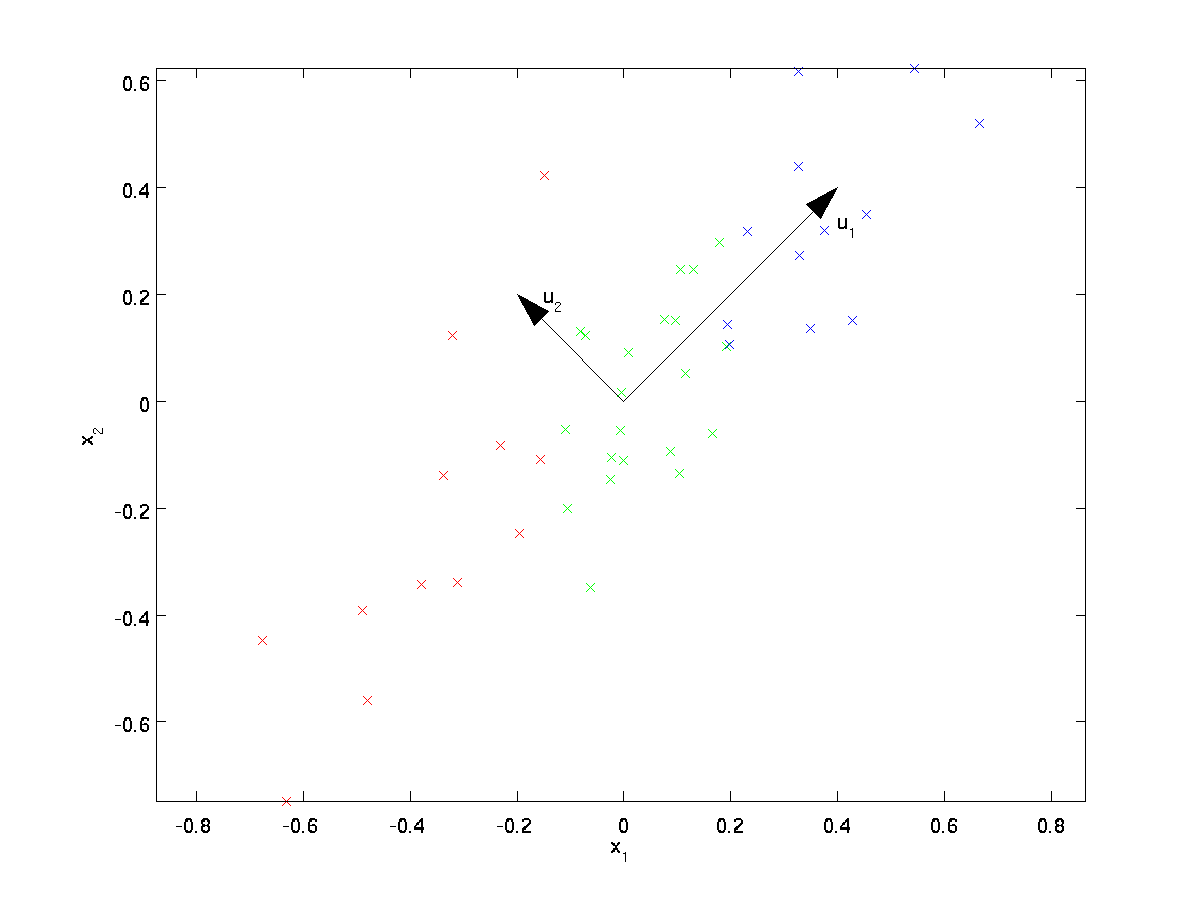
d.w.z. de gegevens variëren veel meer in de richting \textstyle u_1 dan \textstyle u_2. Om de richtingen \textstyle u_1 en \textstyle u_2 formeler te vinden, berekenen we eerst de matrix \textstyle \Sigma als volgt:
\begin{align}\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}
als \textstyle x nulgemiddelde heeft, dan is \textstyle \Sigma precies de covariantiematrix van \textstyle x. (het symbool “\textstyle \Sigma”, uitgesproken als “Sigma”, is de standaardnotatie voor het aangeven van de covariantie.matrix. Helaas lijkt het net op het sommatiesymbool, zoals in \ sum_{i = 1}^n i; maar dit zijn twee verschillende dingen.)
dan kan worden aangetoond dat \ textstyle u_1—de belangrijkste variatierichting van de gegevens—de bovenste (hoofd) eigenvector van \textstyle \Sigma is, en \textstyle u_2 de tweede eigenvector is.
Opmerking: Als u geïnteresseerd bent in een meer formele wiskundige afleiding/rechtvaardiging van dit resultaat, zie de CS229 (Machine Learning) lecture notes op PCA (link onderaan deze pagina). U hoeft dit echter niet te doen om deze cursus te volgen.
u kunt standaard numerieke lineaire algebra software gebruiken om deze eigenvectoren te vinden (zie implementation Notes). Laten we concreet de eigenvectoren van \textstyle \Sigma berekenen en de eigenvectoren in kolommen stapelen om de matrix \textstyle U te vormen:
\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}
Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.
de vectoren \ textstyle u_1 en \ textstyle u_2 in ons voorbeeld vormen een nieuwe basis waarin we de gegevens kunnen vertegenwoordigen. Concreet, laat \ textstyle x \in \ Re^2 een trainingsvoorbeeld zijn. Dan is \textstyle u_1^Tx de lengte (magnitude) van de projectie van \textstyle x op de vector \textstyle u_1.
evenzo is \ textstyle u_2^Tx de magnitude van \ textstyle x geprojecteerd op de vector \ textstyle u_2.
roteren van de Data
dus kunnen we \textstyle x in de \textstyle (u_1, u_2)-basis weergeven door
\begin{align}te berekenen x_{\rm rot} = u^Tx = \begin{bmatrix} u_1^Tx \\ u_2^TX \end{bmatrix} \end{align}
(het subscript “rot” komt van de waarneming dat dit overeenkomt met een rotatie (en mogelijk reflectie) van de oorspronkelijke gegevens.) Laten we de hele trainingsset nemen, en berekenen \textstyle x_{\RM rot}^{(i)} = u^Tx^{(i)} voor elke \ textstyle i. plotten deze getransformeerde data \ textstyle x_ {\RM rot}, krijgen we:

Dit is de trainingsset geroteerd in de \textstyle u_1,\textstyle u_2 basis. In het algemene geval zal \textstyle u^Tx de trainingsset zijn die wordt geroteerd op basis \ textstyle u_1,\textstyle u_2,…, \textstyle u_n.
een van de eigenschappen van \textstyle U is dat het een “orthogonale” matrix is, wat betekent dat het voldoet aan \ textstyle U^T = uu^t = I. Dus als je ooit van de geroteerde vectoren \textstyle x_{\RM rot} terug moet naar de oorspronkelijke data \textstyle x, kun je
\begin{align}X = u x_{\rm rot} ,\end{align}
berekenen omdat \textstyle U x_{\rm rot} = uu^T x = x.
de Gegevensdimensie
reduceert,zien we dat de belangrijkste variatierichting van de gegevens is de eerste dimensie \textstyle x_{\rm rot, 1} van deze geroteerde gegevens. Dus, als we deze gegevens tot één dimensie willen reduceren, kunnen we
\begin{align}\tilde{x}^{(i)} = x_{\RM rot,1}^{(i)} = u_1^TX^{(i)} \in \Re instellen.\end{align}
meer in het algemeen, als \textstyle x \in \Re^n en we willen het reduceren tot een \textstyle K dimensionale representatie \textstyle \tilde{x} \in \Re^k (waarbij k < n), nemen we de eerste \textstyle k componenten van \textstyle x_{\RM rot}, die overeenkomen met de bovenste \textstyle k richtingen van variatie.
een andere manier om PCA uit te leggen is dat \textstyle x_{\RM rot} een \textstyle n dimensionale vector is, waarbij de eerste componenten waarschijnlijk groot zijn (bijv. in ons voorbeeld zagen we dat \textstyle x_ {\RM rot, 1}^{(i)} = u_1^TX^{(i)} redelijk grote waarden heeft voor de meeste voorbeelden \textstyle i), en dat de latere componenten waarschijnlijk klein zijn (bijvoorbeeld, in ons voorbeeld, \textstyle x_{\RM rot, 2}^{(i)} = u_2^TX^{(i)} was waarschijnlijker klein). Wat PCA doet het laat de latere (kleinere) componenten van \textstyle x_{\rm rot} vallen, en benadert ze gewoon met 0 ‘ s. concreet kan onze definitie van \textstyle \tilde{x} ook worden bereikt door gebruik te maken van een benadering van \textstyle x_{\rm rot} waar alle behalve de eerste \textstyle k componenten nullen zijn. In andere woorden, we hebben:
\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\ca \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\rm rot,k} \\x_{\rm rot,k+1} \\\vdots \\ x_{\rm rot,n} \end{bmatrix}= x_{\rm rot} \end{align}
In ons voorbeeld, dit geeft ons het volgende perceel van \textstyle \tilde{x} (met behulp van \textstyle n=2, k=1):

echter, omdat de uiteindelijke \textstyle n-k componenten van \textstyle \tilde{x} zoals hierboven gedefinieerd altijd nul zouden zijn, is het niet nodig om deze nullen rond te houden, en dus definiëren we \textstyle \tilde{x} als een \textstyle k-dimensionale vector met alleen de eerste \textstyle k (niet-nul) componenten.
Dit verklaart ook waarom we onze gegevens wilden uitdrukken in de \textstyle u_1, u_2, \ ldots, u_n basis: beslissen welke componenten te houden wordt gewoon het houden van de bovenste \ textstyle k componenten. Wanneer we dit doen, zeggen we ook dat we “behoud van de top \textstyle k PCA (of principal) componenten.”
herstellen van een benadering van de gegevens
nu is \ textstyle \ tilde{x} \in \ Re^k een lagerdimensionale, “gecomprimeerde” representatie van de oorspronkelijke \ textstyle x \in \ Re^n. gegeven \ textstyle \ tilde{x}, hoe kunnen we een benadering \textstyle \hat{x} herstellen tot de oorspronkelijke waarde van \ textstyle x? Uit een eerdere sectie weten we dat \ textstyle x = u x_ {\RM rot}. Verder kunnen we \textstyle \tilde{x} zien als een benadering van \textstyle x_{\RM rot}, waarbij we de laatste \textstyle n-k componenten op nullen hebben gezet. Dus, gegeven \textstyle \tilde{x} \in \Re^k, kunnen we het pad uit met \textstyle n-k nullen om onze onderlinge aanpassing aan \textstyle x_{\rm rot} \in \Re^n. Eindelijk, we pre-vermenigvuldigen met \textstyle U aan voor onze aanpassing aan de \textstyle x. Concreet, we krijgen
\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}
de uiteindelijke gelijkheid hierboven komt van de definitie van \ textstyle U die eerder gegeven is. (In een praktische implementatie zouden we eigenlijk geen pad \textstyle \tilde{x} op nul zetten en dan vermenigvuldigen met \ textstyle U, omdat dat zou betekenen dat we veel dingen vermenigvuldigen met nullen; in plaats daarvan zouden we \textstyle \tilde{x} \in \Re^k vermenigvuldigen met de eerste \textstyle K kolommen van \textstyle U zoals in de uiteindelijke expressie hierboven.) Door dit toe te passen op onze dataset, krijgen we de volgende plot voor \ textstyle \hat{x}:
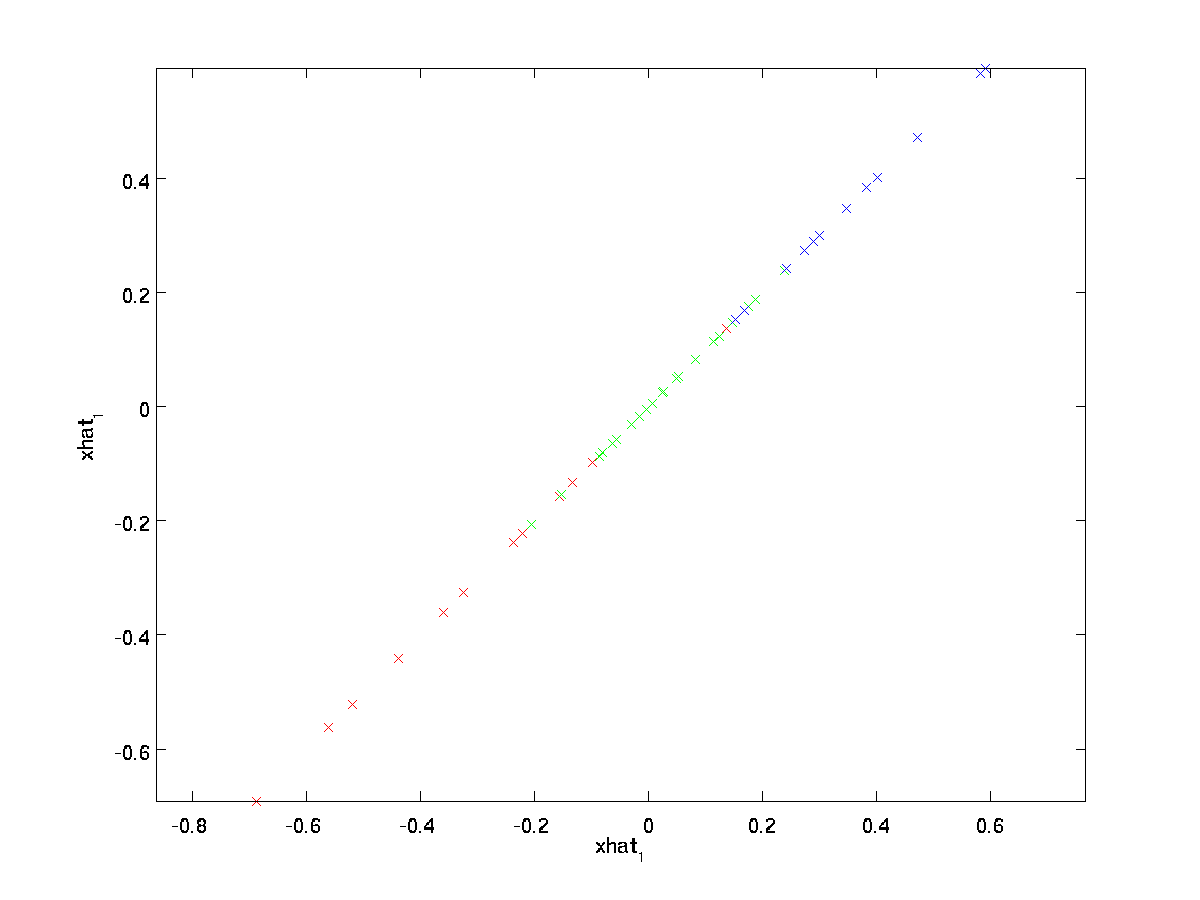
we gebruiken dus een 1-dimensionale benadering van de oorspronkelijke dataset.
Als u een auto-encoder of ander unsupervised feature learning algoritme traint, zal de looptijd van uw algoritme afhangen van de dimensie van de invoer. Als u \textstyle \tilde{x} \in \Re^k invoert in uw leeralgoritme in plaats van \ textstyle x, dan traint u op een lagerdimensionale invoer, waardoor uw algoritme aanzienlijk sneller kan werken. Voor veel datasets kan de lagere dimensionale \textstyle \tilde{x} representatie een zeer goede benadering zijn van het origineel, en het gebruik van PCA op deze manier kan uw algoritme aanzienlijk versnellen terwijl u zeer weinig benaderingsfout introduceert.
aantal te behouden componenten
hoe stellen we \textstyle k in; d.w.z., hoeveel PCA-componenten moeten we behouden? In ons eenvoudige 2 dimensionale voorbeeld leek het natuurlijk om 1 van de 2 componenten te behouden, maar voor hoger dimensionale gegevens is deze beslissing minder triviaal. Als \textstyle k te groot is, dan zullen we de gegevens niet veel comprimeren; in de limiet van \ textstyle k=n, dan gebruiken we gewoon de originele gegevens (maar geroteerd in een andere basis). Omgekeerd, als \textstyle k te klein is, dan kunnen we een zeer slechte benadering van de gegevens gebruiken.
om te beslissen hoe \textstyle k wordt ingesteld, zullen we meestal kijken naar het”‘ percentage van variantie behouden “‘ voor verschillende waarden van \textstyle k. concreet, als \textstyle k=n, dan hebben we een exacte benadering van de gegevens, en we zeggen dat 100% van de variantie behouden blijft. Dat wil zeggen:, alle variatie van de oorspronkelijke gegevens wordt bewaard. Omgekeerd, als \textstyle k=0, dan benaderen we alle gegevens met de nulvector, en dus wordt 0% van de variantie behouden.
meer in het algemeen, laat \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n de eigenwaarden zijn van \textstyle \Sigma (gesorteerd in afnemende volgorde), zodat \textstyle \lambda_j de eigenwaarde is die overeenkomt met de eigenvector \textstyle u_j. als we dan \textstyle k belangrijkste componenten behouden, wordt het percentage van de variantie gegeven door:
\begin{align} \ frac {\sum_{j = 1}^k \ lambda_j} {\sum_{j = 1}^n \ lambda_j}.\ end{align}
in ons eenvoudige 2D voorbeeld hierboven, \ textstyle \ lambda_1 = 7.29, en \textstyle \ lambda_2 = 0.69. Dus, door alleen \textstyle k=1 hoofdcomponenten te behouden, behielden we \textstyle 7.29/(7.29+0.69) = 0.913, of 91,3% van de variantie.
een meer formele definitie van variantiepercentage is buiten het bereik van deze noten. Het is echter mogelijk aan te tonen dat \textstyle \lambda_j =\sum_{i=1}^m x_{\rm rot,j}^2. Dus, als \textstyle \lambda_j \approx 0,dat laat zien dat \textstyle x_{\rm rot, j} is meestal in de buurt van 0 toch, en we verliezen relatief weinig door het benaderen met een constante 0. Dit verklaart ook waarom we de bovenste hoofdcomponenten behouden (die overeenkomen met de grotere waarden van \textstyle \lambda_j) in plaats van de onderste. De bovenste hoofdcomponenten \textstyle x_{\rm rot,j} zijn degenen die variabeler zijn en grotere waarden aannemen, en waarvoor we een grotere benaderingsfout zouden maken als we ze op nul zouden zetten.
in het geval van afbeeldingen is een veelvoorkomende heuristiek het kiezen van \ textstyle k om 99% van de variantie te behouden. Met andere woorden, we kiezen de kleinste waarde van \textstyle k die voldoet aan
\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}
afhankelijk van de toepassing, als u bereid bent om een extra fout op te lopen, worden soms ook waarden in het bereik van 90-98% gebruikt. Als je aan anderen beschrijft hoe je PCA hebt toegepast, zal zeggen dat je \textstyle k hebt gekozen om 95% van de variantie te behouden ook een veel gemakkelijker te interpreteren beschrijving zijn dan zeggen dat je 120 (of welk ander aantal) componenten hebt behouden.
PCA op afbeeldingen
om PCA te laten werken, willen we meestal dat elk van de functies \textstyle x_1, x_2, \ldots, x_n een vergelijkbaar bereik van waarden heeft als de andere (en een gemiddelde van bijna nul hebben). Als u PCA eerder op andere toepassingen hebt gebruikt, kunt u daarom elke functie afzonderlijk hebben voorbehandeld om een nulgemiddelde en eenheidsvariantie te hebben, door afzonderlijk het gemiddelde en de variantie van elke functie \textstyle x_j te schatten. Dit is echter niet de voorbewerking die we op de meeste soorten afbeeldingen zullen toepassen. In het bijzonder, stel dat we ons algoritme trainen op “‘natuurlijke afbeeldingen”‘, zodat \textstyle x_j de waarde is van pixel \textstyle j. met” natuurlijke afbeeldingen ” bedoelen we informeel het type afbeelding dat een typisch dier of persoon tijdens zijn leven zou kunnen zien.
opmerking: Meestal gebruiken we afbeeldingen van buiten scènes met gras, bomen, enz., en knip kleine (zeg 16×16) afbeelding patches willekeurig uit deze om het algoritme te trainen. Maar in de praktijk zijn de meeste feature learning-algoritmen extreem robuust voor het exacte type beeld waarop het is getraind, dus de meeste beelden die met een normale camera zijn gemaakt, zolang ze niet overdreven wazig zijn of vreemde artefacten hebben, zouden moeten werken.
bij het trainen op natuurlijke afbeeldingen heeft het weinig zin om een afzonderlijke gemiddelde en variantie voor elke pixel te schatten, omdat de statistieken in een deel van de afbeelding (theoretisch) hetzelfde moeten zijn als elk ander deel.
Deze eigenschap van afbeeldingen wordt “‘ stationariteit genoemd.”‘
in detail, om PCA goed te laten werken, vereisen we informeel dat (i) de functies ongeveer nul gemiddelde hebben, en (ii) de verschillende functies vergelijkbare verschillen met elkaar hebben. Met natuurlijke beelden, (ii) is al tevreden, zelfs zonder variantie normalisatie, en dus zullen we geen variantie normalisatie uit te voeren.
(Als u traint op audio data-zeg, op spectrograms-of op tekst data-zeg, bag-of-word vectoren-zullen we meestal ook geen variantie normalisatie uitvoeren.)
In feite is PCA invariant voor de schaling van de data, en zal dezelfde eigenvectoren retourneren, ongeacht de schaling van de input. Formeler, als je elke feature Vector \textstyle x vermenigvuldigt met een positief getal (dus elke feature in elk trainingsvoorbeeld schalen met hetzelfde getal), zal PCA ‘ s output eigenvectoren niet veranderen.
dus we zullen geen variantie normalisatie gebruiken. De enige normalisatie die we dan moeten uitvoeren is gemiddelde normalisatie, om ervoor te zorgen dat de functies een gemiddelde rond nul hebben. Afhankelijk van de toepassing zijn we vaak niet geïnteresseerd in hoe helder het totale invoerbeeld is. Bij objectherkenningstaken heeft de totale helderheid van de afbeelding bijvoorbeeld geen invloed op welke objecten er in de afbeelding zijn. Formeel gezien zijn we niet geïnteresseerd in de gemiddelde intensiteitswaarde van een afbeeldingspatch; dus kunnen we deze waarde aftrekken, als een vorm van gemiddelde normalisatie.
concreet, als \textstyle x^{(i)} \in \Re^{n} de (grijswaarden) intensiteitswaarden zijn van een 16×16 afbeeldingspatch (\textstyle n=256), kunnen we de intensiteit van elke afbeelding \textstyle x^{(i)} als volgt normaliseren:
\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}
voor alle \textstyle j
merk op dat de twee bovenstaande stappen afzonderlijk worden gedaan voor elke afbeelding \textstyle x^{(i)}, en dat \textstyle \mu^{(i)} hier de gemiddelde intensiteit van de afbeelding \textstyle x^{(i)} is. In het bijzonder is dit niet hetzelfde als het afzonderlijk schatten van een gemiddelde waarde voor elke pixel \textstyle x_j.
Als u uw algoritme traint op andere afbeeldingen dan natuurlijke afbeeldingen (bijvoorbeeld afbeeldingen van handgeschreven tekens, of afbeeldingen van afzonderlijke Geïsoleerde Objecten gecentreerd tegen een witte achtergrond), kunnen andere vormen van normalisatie het overwegen waard zijn, en kan de beste keuze applicatie-afhankelijk zijn. Maar bij het trainen op natuurlijke beelden, het gebruik van de per-image gemiddelde normalisatie methode zoals gegeven in de vergelijkingen hierboven zou een redelijke standaard.
Whitening
we hebben PCA gebruikt om de dimensie van de gegevens te verkleinen. Er is een nauw verwante preprocessing stap genoemd whitening (of, in sommige andere literatuur, sphering) die nodig is voor sommige algoritmen. Als we trainen op afbeeldingen, is de ruwe invoer redundant, omdat aangrenzende pixelwaarden sterk gecorreleerd zijn. Het doel van whitening is om de input minder redundant te maken; formeler is onze wens dat onze leeralgoritmen een trainingsinput zien waarbij (i) de functies minder gecorreleerd zijn met elkaar, en (ii) de functies allemaal dezelfde variantie hebben.
2D voorbeeld
We zullen eerst whitening beschrijven met behulp van ons vorige 2D voorbeeld. Vervolgens beschrijven we hoe dit gecombineerd kan worden met smoothing, en tenslotte hoe dit gecombineerd kan worden met PCA.
Hoe kunnen we onze invoerfuncties niet met elkaar in verband brengen? We hadden dit al gedaan bij het berekenen van \ textstyle x_ {\RM rot}^{(i)} = u^Tx^{(i)}.
Het herhalen van onze vorige figuur, onze plot voor \textstyle x_{\RM rot} was:

de covariantiematrix van deze gegevens wordt gegeven door:
\begin{align}\begin{bmatrix}7.29 && 0,69\end{bmatrix}.\ end{align}
(opmerking: Technisch gezien zullen veel van de uitspraken in deze sectie over de “covariantie” alleen waar zijn als de gegevens een nulgemiddelde hebben. In de rest van deze sectie, zullen we deze veronderstelling Als impliciet in onze verklaringen. Maar zelfs als het gemiddelde van de gegevens niet precies nul is, zijn de intuïties die we hier presenteren nog steeds waar, en dus is dit niet iets waar je je zorgen over moet maken.)
Het is geen toeval dat de diagonale waarden \textstyle \lambda_1 en \textstyle \lambda_2 zijn. Verder zijn de off-diagonale ingangen nul; \textstyle x_{\RM rot, 1} en \textstyle x_ {\rm rot, 2} zijn dus niet gecorreleerd, wat beantwoordt aan een van onze wensen voor whitened data (dat de kenmerken minder gecorreleerd zijn).
om elk van onze invoerfuncties eenheidsvariantie te laten hebben,kunnen we eenvoudig elke eigenschap \textstyle x_{\rm rot, i} herschalen met \textstyle 1/\sqrt{\lambda_i}. Concreet definiëren we onze whitened data \textstyle x_{\rm PCAwhite} \in \Re^n als volgt:
\begin{align}x_{\rm PCAwhite, i} = \frac{x_{\RM rot, i}} {\sqrt {\lambda_i}}. \ end{align}
plotten \textstyle x_ {\rm PCAwhite}, krijgen we:

deze gegevens hebben nu covariantie gelijk aan de identiteitsmatrix \textstyle I. we zeggen dat \textstyle x_{\rm PCAwhite} onze PCA whitened versie van de gegevens is: de verschillende componenten van \textstyle x_{\rm PCAwhite} zijn niet gecorreleerd en hebben eenheidsvariantie.
Whitening gecombineerd met dimensionaliteitsreductie. Als u gegevens wilt hebben die wit zijn en die lager dimensionaal zijn dan de oorspronkelijke invoer, kunt u optioneel ook alleen de bovenste \textstyle k-componenten van \textstyle x_{\rm PCAwhite} behouden. Wanneer we PCA whitening combineren met regularisatie (later beschreven), zullen de laatste paar componenten van \textstyle x_{\rm PCAwhite} toch bijna nul zijn, en dus veilig kunnen worden gedropt.
ZCA Whitening
ten slotte blijkt dat deze manier om de gegevens covariantie-identiteit \textstyle I te geven niet uniek is. Concreet, als \textstyle R een orthogonale matrix is, zodat het voldoet aan \textstyle RR^T = R^T = I( minder formeel, als \textstyle R een rotatie / reflectie matrix is), dan zal \textstyle R\, x_{\rm PCAwhite} ook identiteitscovariantie hebben.
In ZCA bleken, kiezen we \textstyle R = U. We definiëren
\begin{align}x_{\rm ZCAwhite} = U x_{\rm PCAwhite}\end{align}
het Plotten \textstyle x_{\rm ZCAwhite}, krijgen we:

Het kan worden aangetoond dat van alle mogelijke keuzes voor \textstyle R, deze keuze van de rotatie veroorzaakt \textstyle x_{\rm ZCAwhite} om zo dicht mogelijk bij de oorspronkelijke input data \textstyle x.
Bij het gebruik van ZCA bleken (in tegenstelling tot de PCA witten), we meestal alle \textstyle n afmetingen van de gegevens, en probeer niet om het verminderen van de afmetingen.
Regularizaton
bij het implementeren van PCA whitening of ZCA whitening in de praktijk, zal soms een deel van de eigenwaarden \textstyle \lambda_i numeriek dicht bij 0 liggen, en dus zou de schaalstap waarbij we delen door \sqrt{\lambda_i} het delen door een waarde dicht bij nul inhouden; dit kan ertoe leiden dat de gegevens opblazen (grote waarden aannemen) of anderszins numeriek onstabiel zijn. In de praktijk implementeren we daarom deze schaalstap met een kleine hoeveelheid regularisatie, en voegen een kleine constante \ textstyle \epsilon toe aan de eigenwaarden voordat we hun vierkantswortel en inverse nemen:
\begin{align}x_ {\rm PCAwhite, i} = \ frac{x_{\RM rot, i}} {\sqrt{\lambda_i + \Epsilon}}.\end{align}
wanneer \textstyle x waarden neemt rond \textstyle, kan een waarde van \textstyle \Epsilon \approx 10^{-5} typisch zijn.
voor het geval van afbeeldingen heeft het toevoegen van \textstyle \epsilon ook het effect dat de invoerafbeelding iets gladder (of low-pass filtering) wordt. Dit heeft ook een wenselijk effect van het verwijderen van aliasing artefacten veroorzaakt door de manier waarop pixels worden aangelegd in een afbeelding, en kan de geleerde functies verbeteren (details vallen buiten het bereik van deze noten).
ZCA whitening is een vorm van voorbewerking van de gegevens die het afbeeldt van \textstyle x naar \textstyle x_{\rm ZCAwhite}. Het blijkt dat dit ook een ruw model is van hoe het biologische oog (het netvlies) beelden verwerkt. In het bijzonder, als je oog beelden waarneemt, zullen de meeste aangrenzende “pixels” in je oog zeer vergelijkbare waarden waarnemen, omdat aangrenzende delen van een afbeelding de neiging hebben om sterk gecorreleerd te zijn in intensiteit. Het is dus verspillend voor uw oog om elke pixel afzonderlijk (via uw oogzenuw) naar uw hersenen te moeten verzenden. In plaats daarvan voert uw netvlies een decorrelatie operatie (dit wordt gedaan via retinale neuronen die een functie genaamd berekenen “on center, off surround/off center, on surround”) die vergelijkbaar is met die uitgevoerd door ZCA. Dit resulteert in een minder redundante weergave van het invoerbeeld, dat vervolgens naar je hersenen wordt overgebracht.
implementatie van PCA Whitening
in deze sectie vatten we de algoritmen PCA, PCA whitening en ZCA whitening samen, en beschrijven we ook hoe je ze kunt implementeren met behulp van efficiënte lineaire algebra bibliotheken.
eerst moeten we ervoor zorgen dat de gegevens (ongeveer) nul-gemiddelde hebben. Voor natuurlijke beelden bereiken we dit (ongeveer) door de gemiddelde waarde van elke afbeelding af te trekken.
We bereiken dit door het gemiddelde voor elke patch te berekenen en af te trekken voor elke patch. In Matlab kunnen we dit doen met
avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);vervolgens moeten we \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. als je dit implementeert in Matlab (of zelfs als je dit implementeert in C++, Java, enz., maar toegang hebben tot een efficiënte lineaire algebra bibliotheek), het doen als een expliciete som is inefficiënt. In plaats daarvan kunnen we dit in één klap berekenen als
sigma = x * x' / size(x, 2);(controleer de wiskunde zelf op juistheid.) Hier nemen we aan dat x een gegevensstructuur is die één trainingsvoorbeeld per kolom bevat (dus x is een \textstyle n-by-\textstyle m matrix).
vervolgens berekent PCA de eigenvectoren van \Sigma. Men zou dit kunnen doen met behulp van de Matlab eig-functie. Omdat \Sigma echter een symmetrische positieve semi-definitieve matrix is, is het numeriek betrouwbaarder om dit te doen met behulp van de svd-functie. Concreet, als u
= svd(sigma);implementeert, dan zal de matrix U de eigenvectoren van \Sigma bevatten (één eigenvector per kolom, gesorteerd in volgorde van boven naar beneden eigenvector), en de diagonale items van de matrix S zullen de overeenkomstige eigenwaarden bevatten (ook gesorteerd in afnemende volgorde). De matrix V zal gelijk zijn aan U, en kan veilig genegeerd worden.
(Noot: De svd-functie berekent eigenlijk de enkelvoudige vectoren en enkelvoudige waarden van een matrix, die voor het speciale geval van een symmetrische positieve semi-definitieve matrix—dat is alles waar we het hier over hebben—gelijk is aan zijn eigenvectoren en eigenwaarden. Een volledige bespreking van enkelvoud vectoren vs. eigenvectoren valt buiten het bereik van deze noten.)
tenslotte kunt u \textstyle x_{\RM rot} en \textstyle \tilde{x} als volgt berekenen:
xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keepDit geeft uw PCA-weergave van de gegevens in termen van \textstyle \tilde{x} \in \Re^k. Overigens, als x een \textstyle n-by-\textstyle m matrix is die al je trainingsgegevens bevat, is dit een vectorized implementatie, en de bovenstaande uitdrukkingen werken ook voor het berekenen van x_{\rm rot} en \tilde{x} voor je hele trainingsset in één keer. De resulterende x_ {\RM rot} en \tilde{x} zullen één kolom hebben die overeenkomt met elk trainingsvoorbeeld.
berekenen met de PCA witter data \textstyle x_{\rm PCAwhite}, gebruikt
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;Sinds S de diagonaal bevat de eigenwaarden \textstyle \lambda_i, dit blijkt een compacte manier van computing \textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,ik} }{\sqrt{\lambda_i}} tegelijkertijd voor alle \textstyle ik.
tot slot, u kunt ook berekenen van het ZCA witter data \textstyle x_{\rm ZCAwhite} als:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;