zasada Francka-Condona opisuje intensywności przejść wibronicznych, czyli absorpcję lub emisję fotonu. Stwierdza, że gdy cząsteczka przechodzi transformację elektroniczną, taką jak jonizacja, konfiguracja jądrowa cząsteczki nie doświadcza znaczących zmian. Wynika to z faktu, że jądra są znacznie bardziej masywne niż elektrony, a przejście elektroniczne odbywa się szybciej niż jądra mogą reagować. Kiedy jądro zrównuje się z nową konfiguracją elektroniczną, teoria stwierdza, że musi przejść wibrację.
jeśli wyobrazimy sobie pionowe przejście od ziemi do wzbudzonego stanu elektronowego jako występujące z wibracyjnej funkcji falowej,która daje rozkład prawdopodobieństwa znalezienia jąder w danym obszarze przestrzeni, możemy określić prawdopodobieństwo danego poziomu wibracyjnego z całki nakładającej się \(s_{v’, v}\), która daje nakładanie się wibracyjnej funkcji falowej w stanie wzbudzonym i ziemi. Liczby kwantowe \(v’\) odnoszą się do stanu podstawowego, a liczby kwantowe \(v\) odnoszą się do stanu wzbudzonego. Prawdopodobieństwo przejścia można podzielić na części elektroniczne i jądrowe za pomocą aproksymacji kondona.
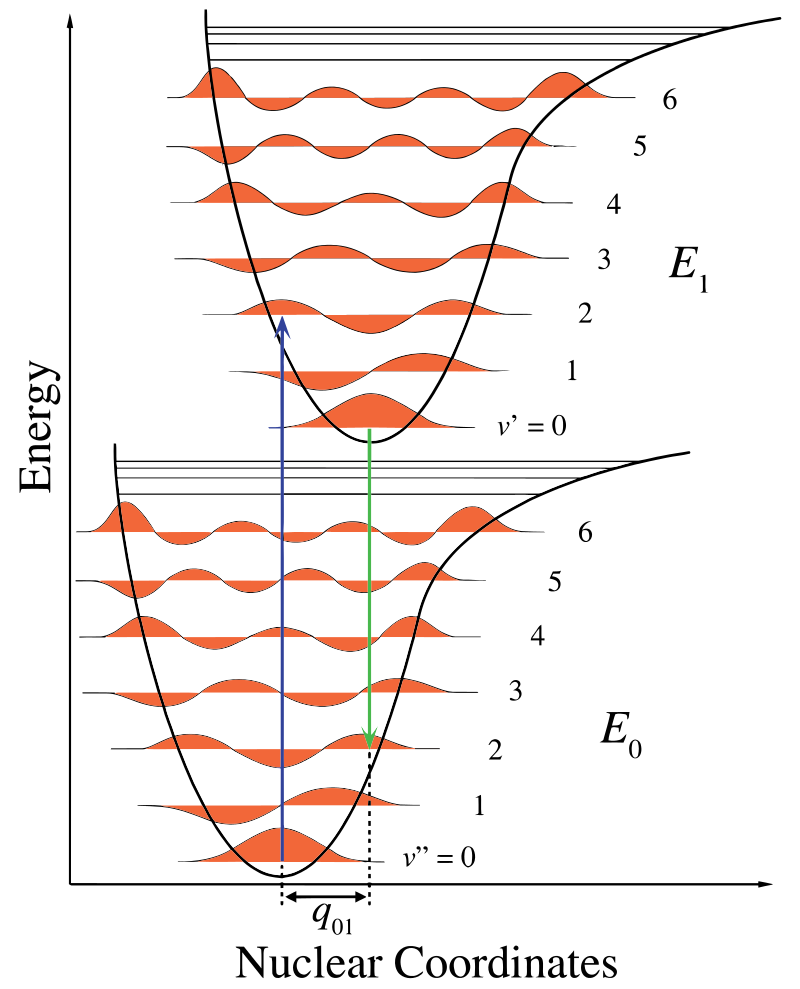
na rysunku \(\PageIndex{1}\) oś jądrowa pokazuje konsekwencję separacji międzyjądrowej, a przejście wibroniczne jest oznaczone niebieskimi i zielonymi pionowymi strzałkami. Ta liczba pokazuje trzy rzeczy:
- absorpcja prowadzi do wyższego stanu energetycznego,
- fluorescencja prowadzi do niższego stanu energetycznego, a
- przesunięcie współrzędnych jądrowych między Ziemią a stanem wzbudzonym wskazuje na nową pozycję równowagi potencjału oddziaływań jądrowych. Fakt, że strzałka fluorescencji jest krótsza niż absorpcja wskazuje, że ma mniej energii, lub że jego długość fali jest dłuższa.
Klasyczne przybliżenie kondona
przybliżenie kondona to założenie, że przejście elektronowe zachodzi w krótkim czasie w porównaniu z ruchem jądrowym, dzięki czemu prawdopodobieństwo przejścia można obliczyć w ustalonej pozycji jądrowej.
ta zmiana drgań jest utrzymywana w stanie określanym jako szybkie wzbudzenie elektroniczne. Powstałe siły Kulombiczne wytwarzają równowagę, jak pokazano na rysunku dla jąder zwanych punktem zwrotnym. Punkt zwrotny można odwzorować, rysując pionową linię od minimum dolnej krzywej do przecięcia wyższego stanu elektronicznego. Procedura ta jest określana jako przejście pionowe i była omawiana wcześniej w kontekście spektroskopii fotoelektronowej (Inna spektroskopia elektroniczna)..
zasada Francka-Condona wyjaśnia względne natężenie przejść wibracyjnych, odnosząc prawdopodobieństwo przejścia wibracyjnego do nakładania się funkcji fal wibracyjnych. Stwierdza, że prawdopodobieństwo przejścia wibracyjnego jest ważone przez całkę pokrywającą Francka-Condona:
\
w ramach przybliżenia Francka-Condona jądra są uważane za „stałe” podczas przejść elektronicznych. Tak więc przejścia elektroniczne można uznać za przejścia pionowe na krzywych energii potencjalnej elektroniki (przejścia vieryczne na rysunku \(\PageIndex{1}\)).
kwantowa zasada Francka-Condona
zasada Francka-Condona ma zarówno klasyczne, jak i kwantowe zastosowanie. Klasycznie zasada Francka-Condona jest przybliżeniem, że przejście elektronowe najprawdopodobniej zachodzi bez zmian położenia jąder w jednostce molekularnej i jej otoczeniu. Powstały stan nazywa się stanem Francka-Condona, a związane z nim przejście-przejściem pionowym. Kwantowo mechaniczne sformułowanie tej zasady polega na tym, że intensywność przejścia wibronowego jest proporcjonalna do kwadratu całki zachodzącej między falami wibracyjnymi dwóch stanów biorących udział w przejściu.
zasada Francka-Condona opiera się na aproksymacji Borna-Oppenheimera, która pozwala na rozdzielenie funkcji falowych elektronowych \(q\) i atomowych \(Q\), biorąc pod uwagę całkowitą funkcję falową.
\
ponieważ operator przejścia, \(\hat {\mu}(q)\), jest zależny tylko od komponentu elektronicznego, składniki jądrowe można oddzielić od całki momentu przejścia, która dyktuje prawdopodobieństwo wystąpienia przejścia:
&= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{Nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align}\]
jeśli Całka jądrowa jest zerowa dla tego przejścia, to przejście nie będzie obserwowane, niezależnie od wielkości współczynnika elektronowego.
\(S_{00}\) Przejście ocenione w modelu oscylatora harmonicznego
jądrowe nakładanie się przejścia zero-zero \(S_{00}\) można obliczyć po prostu za pomocą definicji postaci Gaussa funkcji falowych oscylatora harmonicznego.
falowanie punktu zerowego w stanie uziemienia jest
\
falowanie punktu zerowego w wzbudzonym stanie elektronicznym jest
\
gdzie
- \(\alpha = \dfrac{\sqrt{MK}}{\hbar}\)
- \(r_e\) jest długością wiązania równowagowego w stanie elektronowym ziemi
- \(q_e\) jest długością wiązania równowagowego w stanie elektronowym wzbudzonym
Całka pokrywająca się z energią jądrową to
\
wykładnik w równaniu \(\ref{FC1}\) może być rozszerzony jako
\
i używamy
\
i
\
do zastąpienia i uzupełnienia kwadratu wewnątrz całki. Możemy wyrazić
\.\]
zatem Całka w równaniu \(\ref{FC2}\) jest
\
Całka jest całką Gaussa. Możesz pokazać, że jeśli pozwolimy \(z = \sqrt{\alpha}\{r-1/2(R_e + Q_e)\}\) to \(dz = \sqrt{\alpha} dR\) i Całka stanie się
\
ta Całka została już rozwiązana, z tabeli całek równanie \(\ref{FC3}\) staje się
\
Wykonalibyśmy tę samą procedurę, aby obliczyć nakładanie się wibracji poziomu zerowego w ziemi na pierwszy wzbudzony poziom wibracji stanu wzbudzonego: \(s_{01}\).
\(S_{01}\) Transition Evaluated within Harmonic Oscillator Model
aby obliczyć nakładanie się zera poziomu stanu ziemi (\(v=0\)) z pierwszym poziomem stanu wzbudzonego (\(v’=1\)) używamy wielomianu Hermite ’ a \(H_1(x) =2x\) do opisania funkcji falowej stanu wzbudzonego (patrz tutaj, aby zapoznać się z funkcjami falowymi oscylatora harmonicznego). Tutaj \(x = \sqrt{\alpha} (R – Q_e)\).
\
z funkcją falowania punktu zerowego w stanie uziemienia jest
\
pierwsza funkcja falowania w stanie wzbudzonym w stanie wzbudzonym jest
\
nakładanie się zera na poziom stanu podstawowego z pierwszym poziomem stanu wzbudzonego (równanie \(\ref{FC01}\)) jest wtedy
\
i
\
takie same podstawienia mogą być wykonane jak powyżej, tak aby całka mogła być zapisana jako (nie pokazana i do zademonstrowania w ćwiczeniach domowych) oraz wynik końcowy to
\
możemy kontynuować i obliczyć, że poziom zerowy w stanie podstawowym pokrywa się ze wszystkimi wyższymi poziomami wibracji światła: \(s_{02}\), \(S_{03}\) itd. Każdy termin odpowiada przejściu z inną energią, ponieważ poziomy wibracyjne mają różne energie. Pasmo absorpcji ma wówczas postać progresji (progresji Francka-Condona) przejścia między różnymi poziomami, każdy z własnym prawdopodobieństwem.
progresje Francka-Condona
aby zrozumieć znaczenie powyższego wzoru dla współczynnika FC, zbadajmy powierzchnię potencjalnej energii stanu wzbudzonego i wzbudzonego w \(T = 0\) Kelvinie. Poniżej pokazane są dwa stany oddzielone energią 8000 cm – 1. Jest to separacja energetyczna między dnami ich potencjalnych studni, ale także między odpowiednimi poziomami energii punktu zerowego. Załóżmy, że liczba falowa trybu wibracyjnego wynosi 1000 cm-1 i że długość wiązania jest zwiększona z powodu faktu, że elektron jest usuwany z orbitalu wiążącego i umieszczany w orbitalu antywibracyjnym po wzbudzeniu elektronicznym.
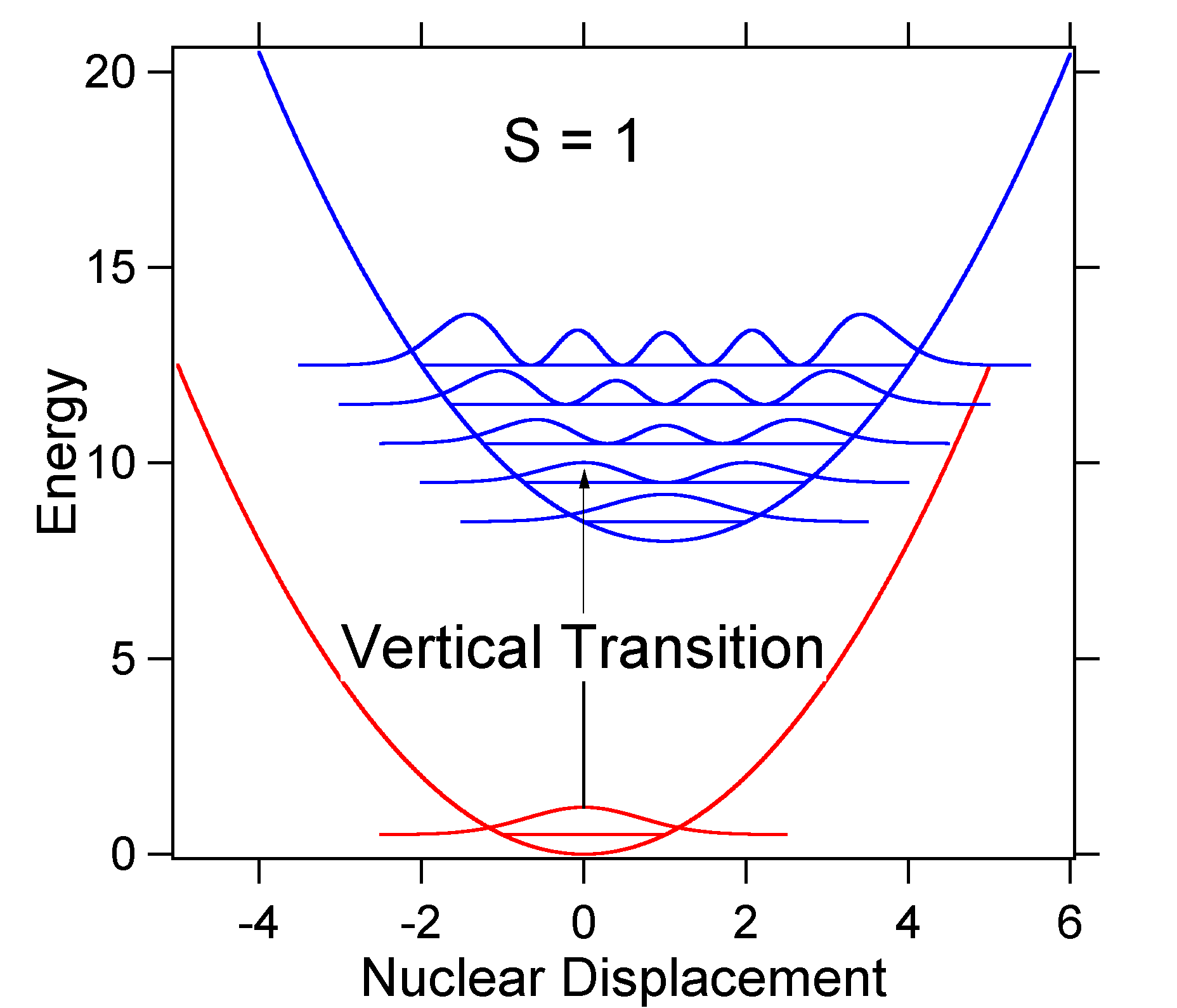
zgodnie z powyższym modelem dla współczynnika Francka-Condona wygenerowalibyśmy widmo „stick” (rysunek \(\PageIndex{3}\)), gdzie każde przejście wibracyjne jest nieskończenie wąskie i przejście może nastąpić tylko wtedy, gdy \(E = h\nu\) dokładnie. Na przykład, powierzchnie energii potencjalnej zostały podane dla S = 1, A prawdopodobieństwo przejścia na każdym poziomie jest podane przez kije (czarne) na rysunku poniżej.
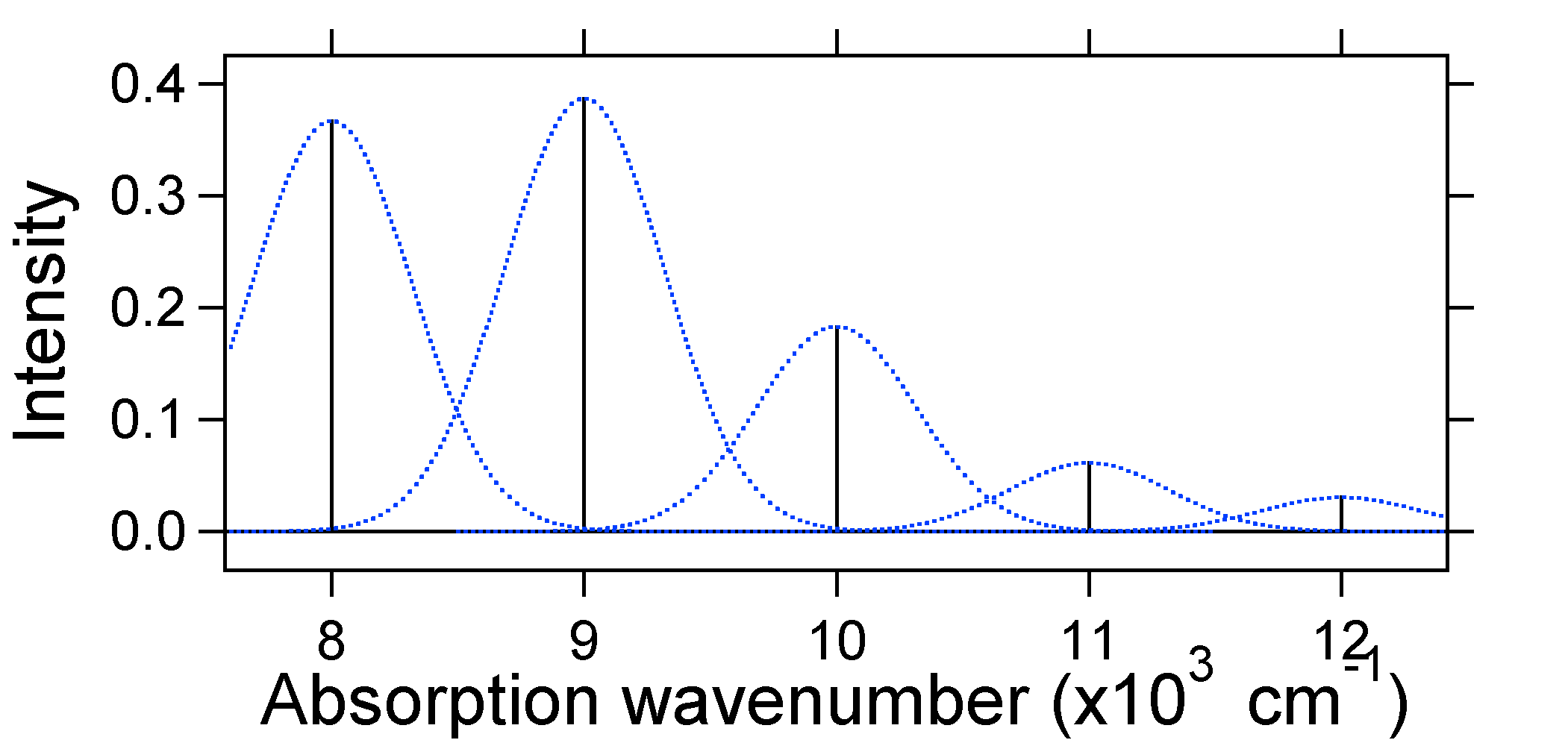
kropkowane Gaussy otaczające każdy kij dają bardziej realistyczny obraz tego, jak powinno wyglądać widmo absorpcji. W tym pierwszym miejscu każdy poziom energii (kij) będzie mieć pewną Szerokość przez fakt, że stan ma skończoną żywotność. Takie poszerzenie nazywa się jednorodnym poszerzeniem, ponieważ w podobny sposób wpływa na wszystkie cząsteczki w zespole. Istnieje również poszerzenie ze względu na niewielkie różnice w środowisku każdej cząsteczki. Ten rodzaj poszerzenia nazywany jest poszerzeniem niejednorodnym. Niezależnie od pochodzenia powyższy model został stworzony za pomocą Gaussa poszerzenia
przesunięcie jądrowe między Ziemią a stanem wzbudzonym determinuje kształt widma absorpcyjnego. Zbadajmy zarówno mniejsze, jak i duże przesunięcie stanu wzbudzonego. Jeśli \(S=½\) i powierzchnie energii potencjalnej w tym przypadku są następujące:
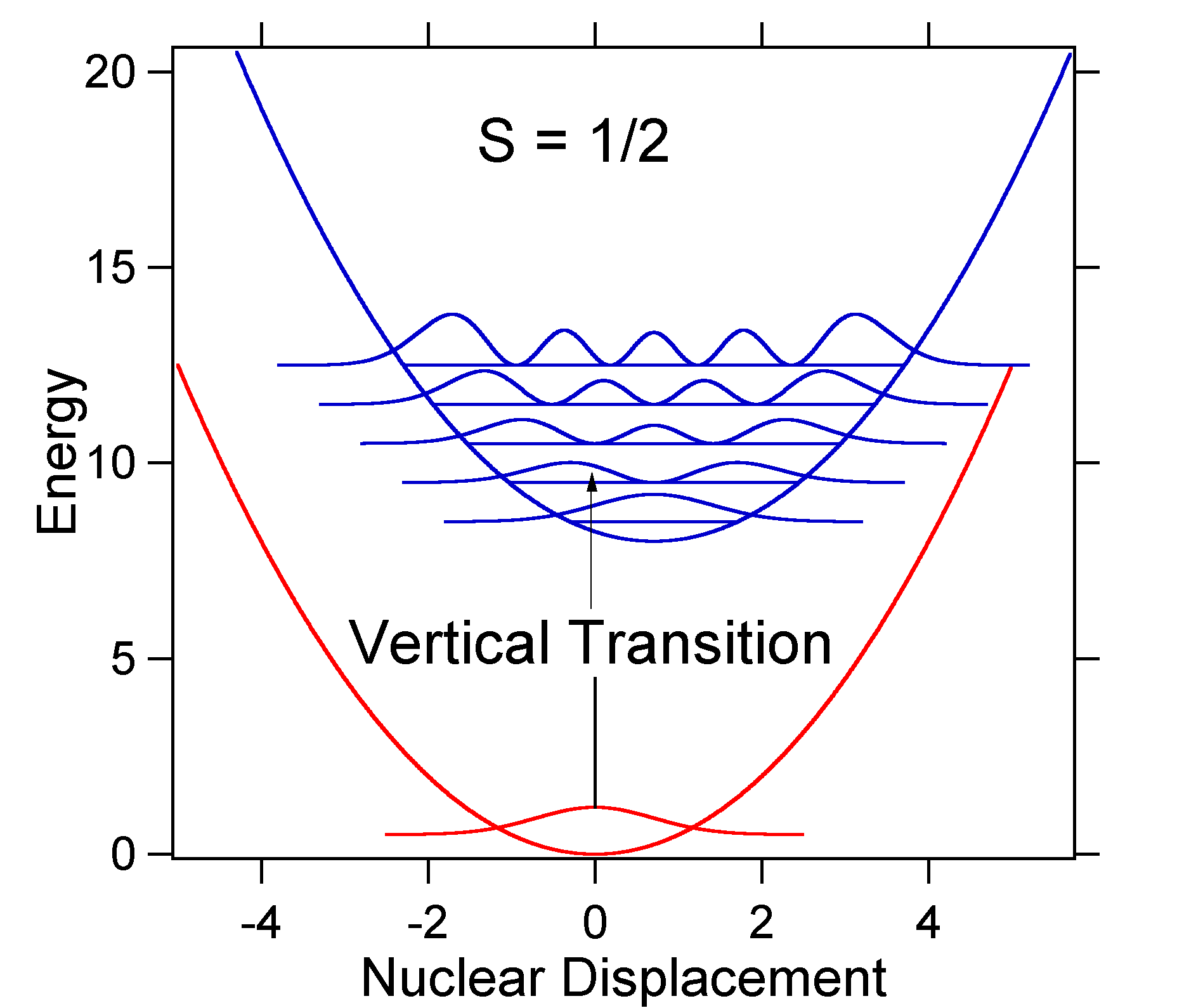
For this case the „stick” spectrum has the appearance in Figure \(\PageIndex{5}\)
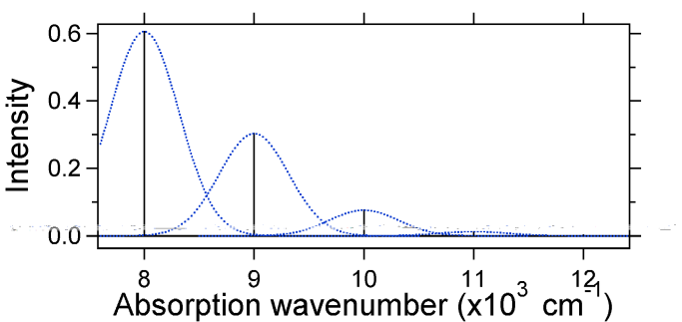
zauważ, że zerowe lub \(s_{0,0}\) Przejście wibracyjne jest znacznie duże w przypadku, gdy przemieszczenie jest małe.
jako ogólna zasada stała \(s\) podaje stosunek intensywności przejścia \(v = 2\) do przejścia \(v = 1\). W tym przypadku, ponieważ \(S = 0.5\), Przejście \(v=2\) jest 0.5 natężeniem przejścia \(v=1\).
jako przykład większego przemieszczenia poniżej przedstawiono rozmieszczenie powierzchni energii potencjalnej dla S = 2.
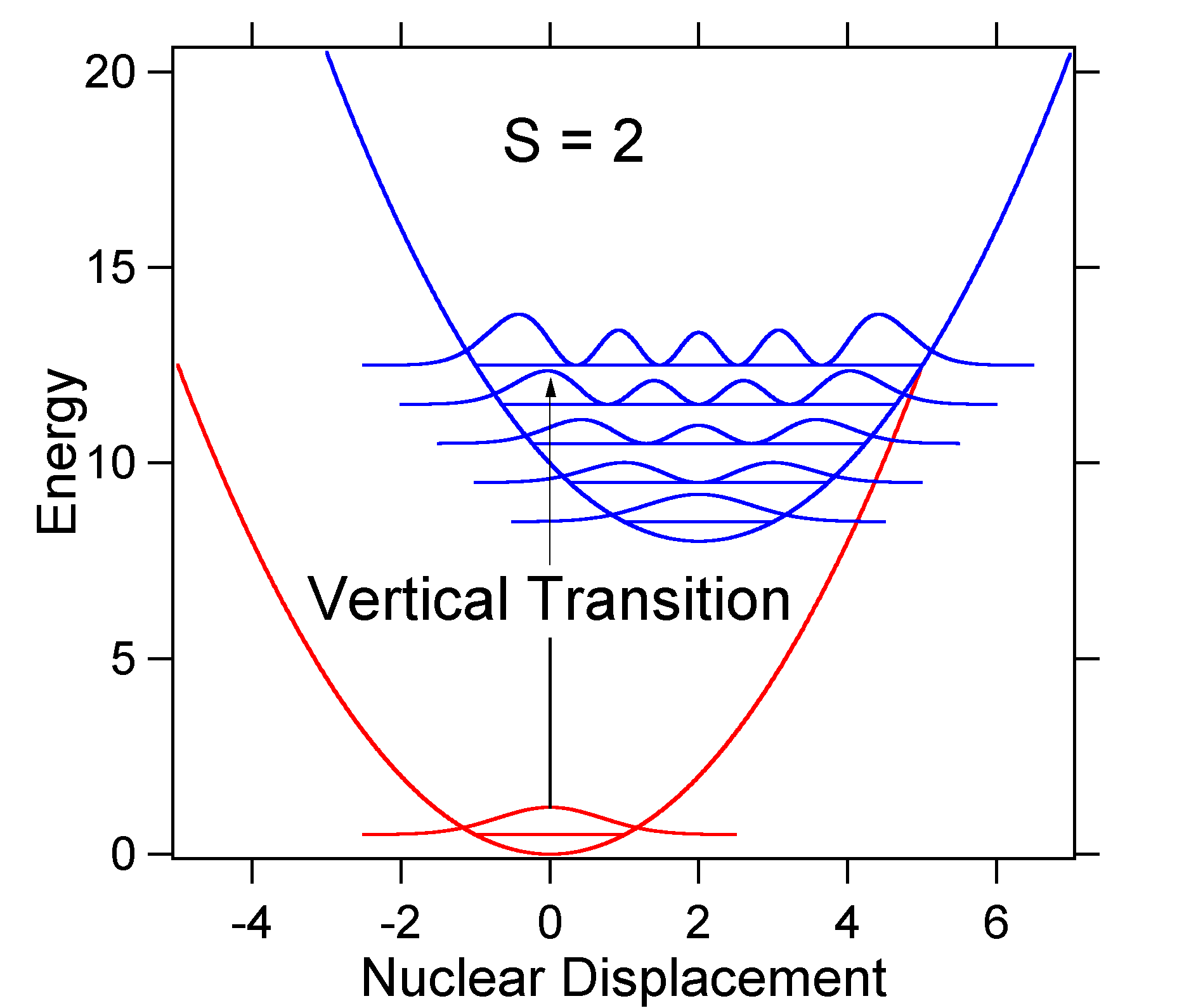
większe przemieszczenie powoduje zmniejszone nakładanie się poziomu stanu podłoża z poziomem V = 0 stanu wzbudzonego. Maksymalna intensywność zostanie osiągnięta w wyższych poziomach wibracji, jak pokazano w widmie drążka.
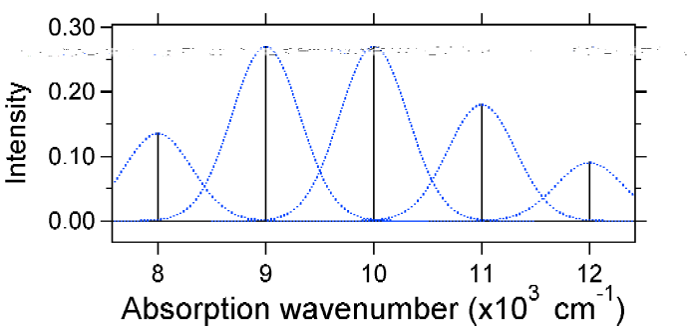
widma absorpcji przedstawione poniżej mają taką samą intensywność zintegrowaną, jednak ich kształty są zmienione ze względu na różny stopień przesunięcia powierzchni energii potencjalnej stanu wzbudzonego.
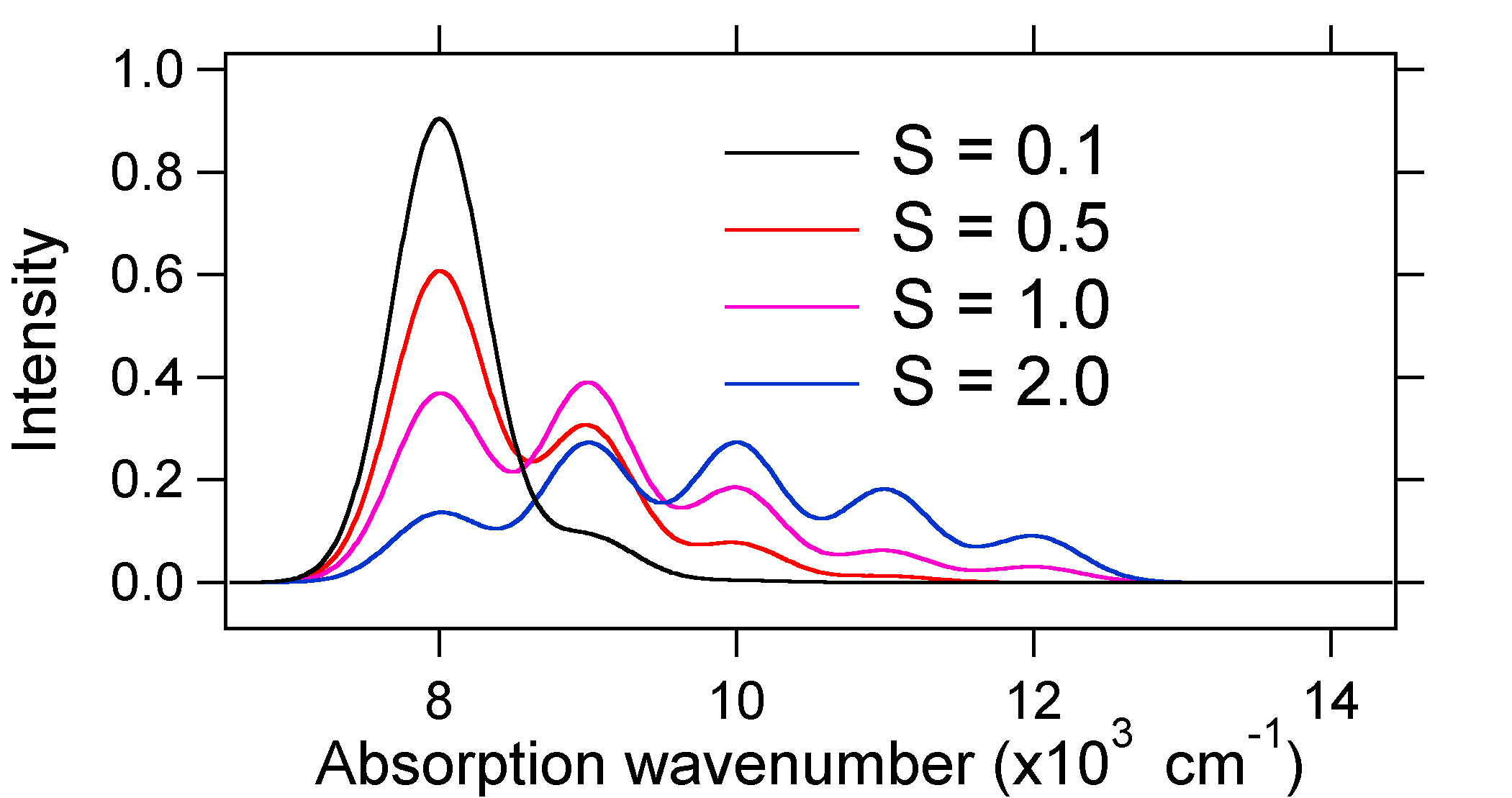
więc natura względnej intensywności pasma wibronowego może nam powiedzieć, czy istnieje przemieszczenie równowagi atomowej, które towarzyszyło przemianie. Kiedy nastąpi zwiększenie długości wiązania (np. \(Q_e > R_e\))? Dzieje się tak, gdy elektron jest promowany z wiązania orbitalu molekularnego do nie wiązania lub anty-wiązania orbitali molekularnych (to znaczy, gdy kolejność wiązania jest mniejsza w stanie wzbudzonym niż w stanie podstawowym).
- niezwiązany orbital cząsteczkowy \(\rightarrow\) Wiązanie orbital cząsteczkowy
- Antyzwiązkowy orbital cząsteczkowy \(\rightarrow\) Wiązanie orbital cząsteczkowy
- Antyzwiązkowy orbital cząsteczkowy \(\rightarrow\) niezwiązany orbital cząsteczkowy
krótko mówiąc, gdy kolejność wiązania jest niższa w stanie wzbudzonym niż w stanie podstawowym, to \(Q_e> r_e\); w takim przypadku nastąpi zwiększenie długości wiązania.
- J. M. Luis, D. M. Bishop, B. Kirtman. Inne podejście do obliczania czynników Francka-Condona, w tym anharmoniczności. J. Chem. Phys., 120 (2004), s. 813-822.
- Atkins, Peter and Julio de Paula. Chemia Fizyczna dla nauk przyrodniczych. 2006. New York, NY: W. H. Freeman and Company. P. 563-564
- zasada Francka-Condona. 1996, 68, 2243. IUPAC Compendium of Chemical Terminology 2nd Edition (1997). www.iupac.org/goldbook/F02510.pdf
- E. Rabinowicz i Govindjee. Pochłanianie światła i Los wzbudzenia energii. 1969. Zasada Francka-Condona. http://www.life.uiuc.edu/govindjee/b…em494/Abs.html
Contributors
- Matthew Ziering
-
Stefan Franzen (North Carolina State University)