Co To jest model ARIMAX?

czym jest model ARIMAX?

jeśli czytałeś naszą serię samouczków na blogu na temat modeli szacowania danych szeregów czasowych, znasz już 3 główne podejścia – autoregresję, średnie kroczące i integrację.

Jaki jest wspólny motyw tych wszystkich modeli?

opierały się wyłącznie na jednej zmiennej.

jednak model może również brać pod uwagę więcej niż tylko przeszłe ceny lub przeszłe pozostałości.

i są to tak zwane modele „MAX”, przy czym ARMAX jest wersją niezintegrowaną, a arimax-jej zintegrowanym odpowiednikiem.

w tym samouczku zbadamy, jak wyglądają i pokażemy, jak krok po kroku zaimplementować je w Pythonie.

zaczynajmy, dobrze?

dlaczego ARMAX i ARIMAX nazywają się modelami „MAX”?

nazwy ARMAX i ARIMAX pochodzą jako rozszerzenia ARMA i ARIMA odpowiednio. X dodany na końcu oznacza „egzogenny”. Innymi słowy, sugeruje dodanie osobnej zmiennej zewnętrznej, aby pomóc zmierzyć naszą zmienną endogenną.

równanie modelu ARMAX i ARIMAX:

ponieważ jedyną różnicą między ARMAX i ARIMAX jest to, że jeden jest zintegrowany, a drugi nie, możemy zbadać jeden z nich, a następnie podkreślić, jak różni się drugi.

zbadaliśmy model zintegrowany w naszym ostatnim artykule na blogu (ARIMA), więc zobaczmy, jak wygląda równanie ARIMAX.

ΔPt = c+ßX + ϕ1 ΔPt – 1 + θ1tt-1+ϵt

oczywiście równanie dla ARMAX byłoby takie samo, z tym że użylibyśmy zmiennej rzeczywistej, powiedzmy P, zamiast jej delta.

Pt=c+ßX+ϕ1 Pt-1+ θ1tt-1 +ϵt

rozkładając równanie ARIMAKSA:

możemy myśleć o ARIMAKSIE jako szczególnym przypadku arimaksu, gdzie kolejność całkowania wynosi 0.

w dalszej części tutoriala skupimy się na ARIMAXIE.

i zaczniemy od rozbicia różnych części w nim. Na początek, Pt i Pt-1 reprezentują wartości odpowiednio w bieżącym okresie i 1 okresie temu.

podobnie, ϵt i ϵt-1 są terminami błędów dla tych samych dwóch okresów. I, oczywiście, c jest tylko podstawowym stałym czynnikiem.

dwa parametry, ϕ1 i θ1, wyrażają, jakie części wartości Pt-1 i błąd ϵt-1 ostatniego okresu są istotne w szacowaniu bieżącego.

teraz dwa nowe dodatki do modelu to ” X ” i jego współczynnik β. Podobnie jak ϕ, β jest współczynnikiem, który będzie szacowany na podstawie wyboru modelu i danych. Ale co z X?

co to jest zmienna egzogenna?

Cóż, X jest zmienną egzogenną i może być dowolną zmienną, którą jesteśmy zainteresowani.

może to być pomiar zmienny w czasie, taki jak stopa inflacji lub cena innego indeksu. Lub zmienna kategoryczna oddzielająca różne dni tygodnia. Może to być również logiczne rozliczanie specjalnych okresów świątecznych. Wreszcie może oznaczać kombinację kilku różnych czynników zewnętrznych.

chodzi o to, że może to być każda inna zmienna lub zmienne, które mogą wpływać na ceny, o ile mamy dostępne dane.

takie czynniki zewnętrzne są znane jako zmienne egzogenne w naszej regresji. Używamy ich wartości, aby przewidzieć i wyjaśnić ten, który nas interesuje, czyli w naszym przypadku aktualne ceny.

jak zaimplementować modele ARMAX i ARIMAX w Pythonie?

Pakiet statsmodels zawiera metodę Arima, która jest w pełni zdolna do obsługi takich dodatkowych wejść.

zaczynamy od określenia charakterystyki modelu i kolejności modelu:

Po tym, jak to zrobimy, musimy również podać exogeneous argument o nazwie „exog”.

wartość, którą chcemy przekazać, musi być jakąś tablicą, ponieważ chcemy mieć wartości powiązane z każdym okresem czasu.

na przykład możemy użyć s&ceny P jako tej zmiennej egzogennej, ponieważ mamy je już w naszych danych.

teraz jesteśmy gotowi dopasować model ARIMAX (1,1,1).

upewnij się, że nazwa zmiennej modelu różni ją od podobnych modeli. W tym przypadku wybieramy, aby to zrobić, dodając „X, spx” na końcu, aby wskazać, że zmienna egzogenna jest S&P.

następnie, jak widać z fragmentów, ustawiamy ją równą metodzie ARIMA jak poprzednio, dodajemy szereg czasowy i kolejność, jak jesteśmy przyzwyczajeni. Na koniec, między tymi dwoma, ustawiamy argument” exog „równy” DF SPX”, który wskazuje S&ceny P.

Jeśli zmieścimy ten model i wydrukujemy jego tabelę podsumowującą, zobaczymy, że otrzymamy dodatkowy wiersz dla Ceny s&P.

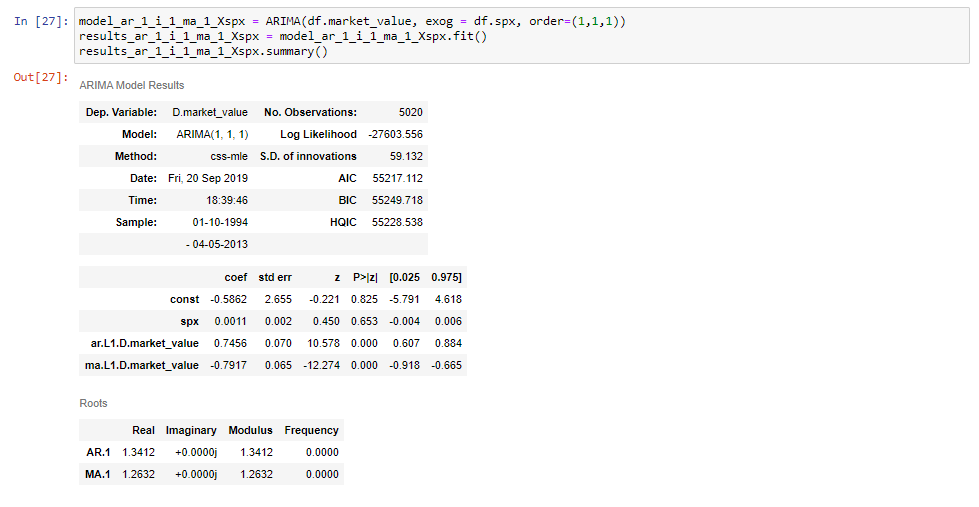
i to wszystko!

udało nam się zaimplementować model ARIMAX w Pythonie.

Jeśli chcesz dowiedzieć się więcej o ARIMAX i innych modelach serii czasowych w Pythonie, sprawdź nasze samouczki Pythona krok po kroku. Jeśli jesteś nowy w Pythonie i chcesz dowiedzieć się więcej, ten obszerny artykuł na temat nauki programowania w Pythonie poprowadzi cię od instalacji, przez Pythonowe IDE, Biblioteki i frameworki, po najlepsze ścieżki kariery i perspektywy pracy w Pythonie.

gotowy na kolejny krok w kierunku kariery w data science?

sprawdź już dziś kompletny program do nauki danych. Zacznij od podstaw z naszymi kursami statystycznymi, matematycznymi i Excel. Zbuduj doświadczenie krok po kroku z SQL, Python, R, Power BI i Tableau. Ulepsz swój zestaw umiejętności za pomocą uczenia maszynowego, głębokiego uczenia, modelowania ryzyka kredytowego, analizy szeregów czasowych i analizy klientów w Pythonie. Nadal nie jesteś pewien, czy chcesz przekształcić swoje zainteresowanie nauką o danych w karierę? Możesz poznać program nauczania lub zapisać się na 15 godzin od początkującego do zaawansowanego wideo za darmo, klikając przycisk poniżej.