
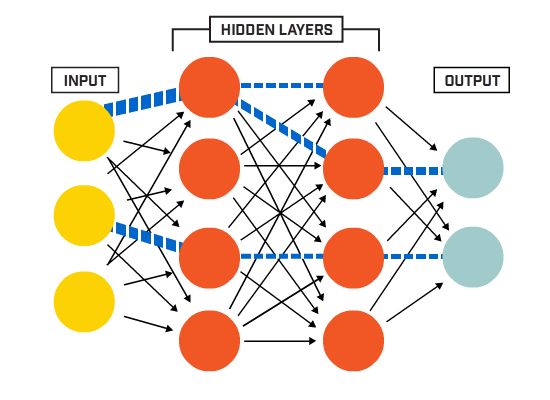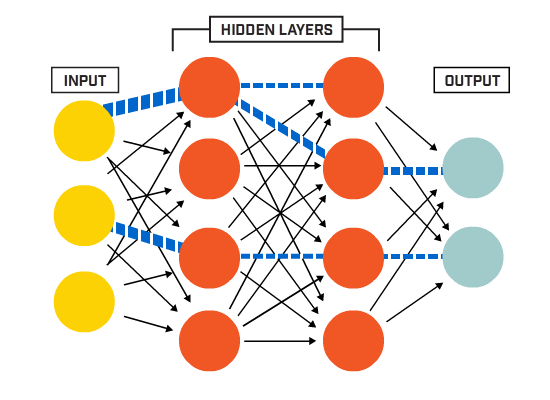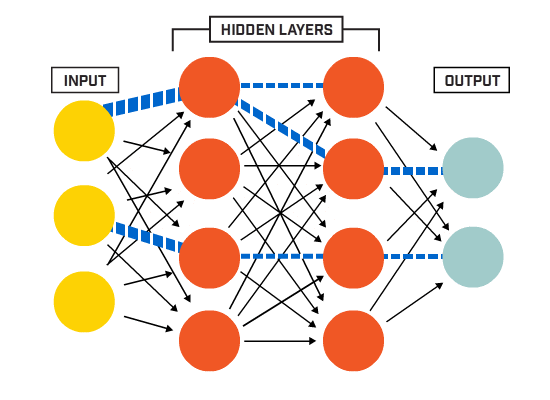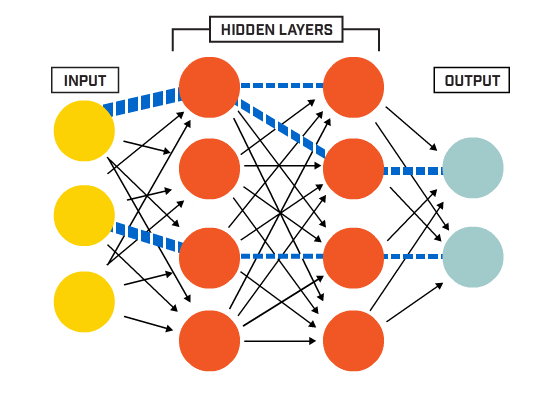
sztuczna sieć neuronowa (Ann) składa się z wielu połączonych ze sobą neuronów:
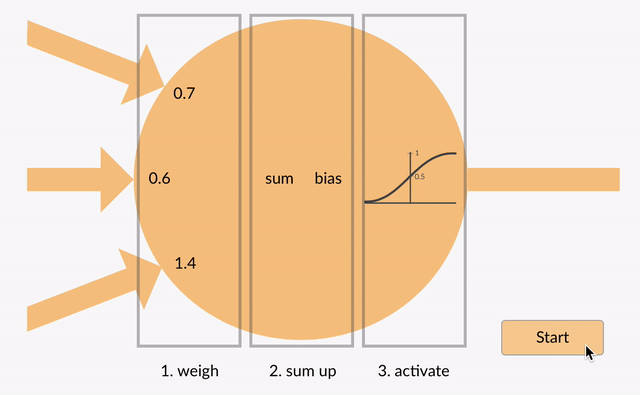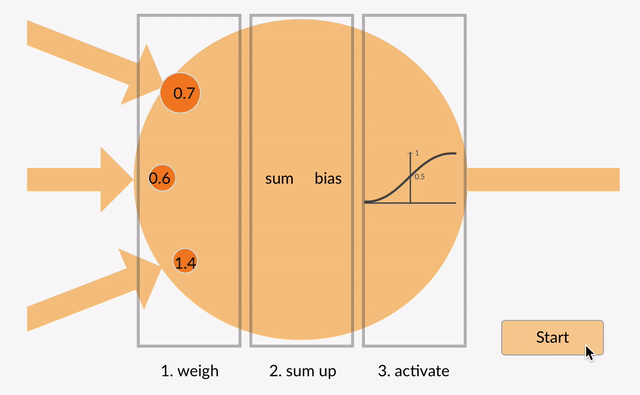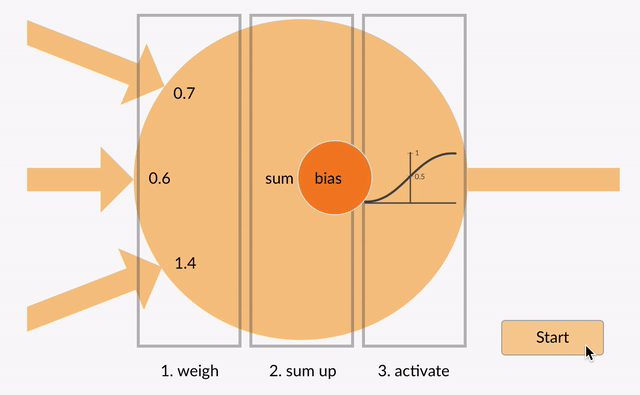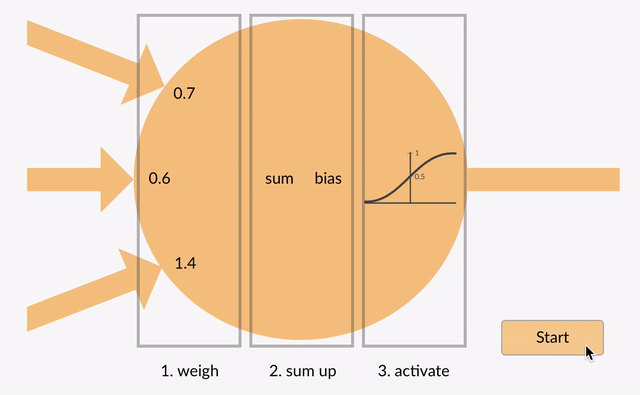
każdy neuron przyjmuje pewne liczby zmiennoprzecinkowe (np.0) i mnoży je przez inne liczby zmiennoprzecinkowe (np. 0.7, 0.6, 1.4) znane jako wagi (1.0 * 0.7 = 0.7, 0.5 * 0.6 = 0.3, -1.0 * 1.4 = -1.4). Wagi działają jako mechanizm skupiania się na określonych wejściach lub ich ignorowania.

ważone dane wejściowe są sumowane (np. 0.7 + 0.3 + -1.4 = -0.4) wraz z wartością odchylenia (np. -0.4 + -0.1 = -0.5).
zsumowana wartość (x) jest teraz przekształcana w wartość wyjściową (y) zgodnie z funkcją aktywacji neuronu (y = f(x)). Niektóre popularne funkcje aktywacji są pokazane poniżej:

np. -0.5 → -0.05 jeśli użyjemy funkcji aktywacji nieszczelnej rektyfikowanej jednostki liniowej (leaky Relu): Y = F(X) = F(-0,5) = max(0,1*-0,5, -0,5) = Max(-0,05, -0,5) = -0.05
wartość wyjściowa neuronu (np. -0,05) jest często wejściem dla innego neuronu.
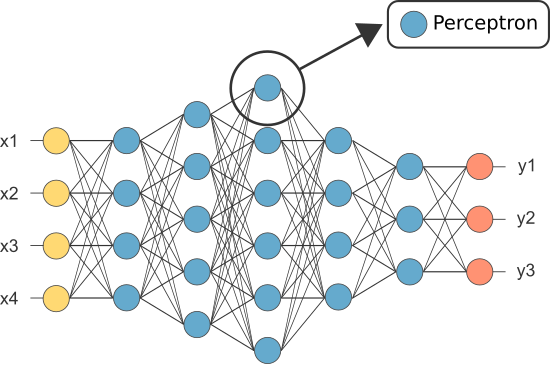
jednak jedna z pierwszych Ann była znana jako Perceptron i składała się tylko z jednego neuronu.pojedynczy neuron.

wynik (tylko) neuronu perceptronu działa jako ostateczna prognoza.

:
import numpy as npclass Neuron:
def __init__(self, n_inputs, bias = 0., weights = None):
self.b = bias
if weights: self.ws = np.array(weights)
else: self.ws = np.random.rand(n_inputs)
def __call__(self, xs):
return self._f(xs @ self.ws + self.b)
def _f(self, x):
return max(x*.1, x)
(uwaga: nie uwzględniliśmy żadnego algorytmu uczenia się w naszym powyższym przykładzie — omówimy algorytmy uczenia się w innym samouczku)
perceptron = Neuron(n_inputs = 3, bias = -0.1, weights = )perceptron()

więc po co nam tyle neuronów w ANN, jeśli wystarczy (jako klasyfikator)?

Niestety poszczególne neurony są w stanie klasyfikować tylko liniowo rozdzielne dane.

jednak łącząc neurony, zasadniczo łączymy ich granice decyzyjne. Dlatego ANN złożona z wielu neuronów jest w stanie nauczyć się złożonych, nieliniowych granic decyzji.

neurony są połączone ze sobą zgodnie z określoną architekturą sieci. Chociaż istnieją różne architektury, prawie wszystkie z nich zawierają warstwy. (NB: Neurony w tej samej warstwie nie łączą się ze sobą)
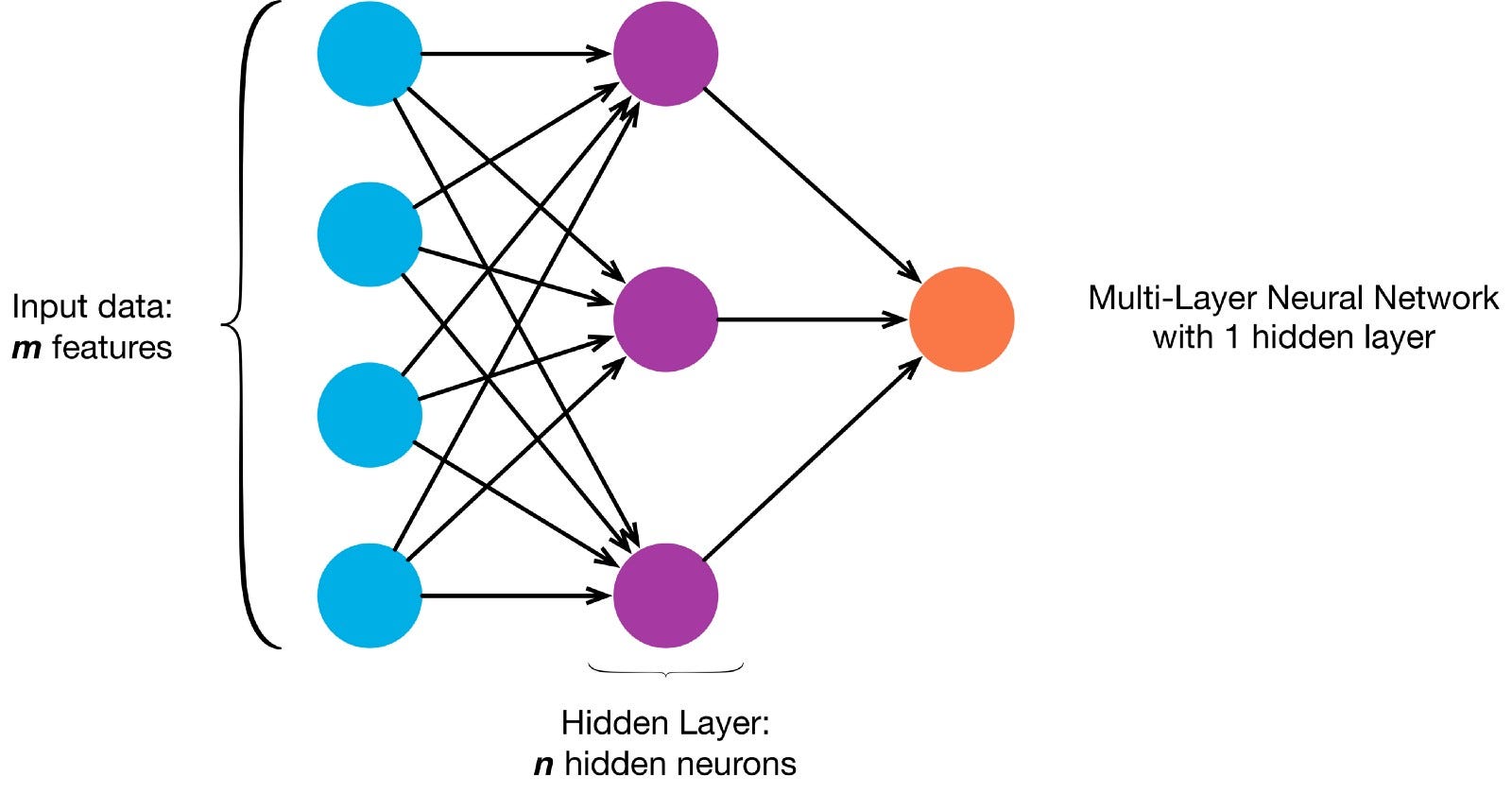
zazwyczaj istnieje warstwa wejściowa (zawierająca kilka warstw). neurony równe liczbie funkcji wejściowych w danych), warstwa wyjściowa (zawierająca liczbę neuronów równą liczbie klas) i warstwa ukryta (zawierająca dowolną liczbę neuronów).

może istnieć więcej niż jedna ukryta warstwa, aby umożliwić sieci neuronowej poznanie bardziej złożonych granic decyzji (dowolne sieć z więcej niż jedną warstwą ukrytą jest uważana za głęboką sieć neuronową).
Lets build a deep NN to paint this picture:

pozwala pobrać obraz i załaduj jego piksele do tablicy
!curl -O https://pmcvariety.files.wordpress.com/2018/04/twitter-logo.jpg?w=100&h=100&crop=1from PIL import Image
image = Image.open('twitter-logo.jpg?w=100')import numpy as np
image_array = np.asarray(image)
teraz uczenie Ann malowania jest zadaniem nadzorowanym, więc musimy utworzyć oznakowany zestaw treningowy (nasze dane szkoleniowe będą miały etykiety wejściowe i oczekiwane etykiety wyjściowe dla każdego wejścia). Wejścia treningowe będą miały 2 wartości (współrzędne X, y każdego piksela).
biorąc pod uwagę prostotę obrazu, moglibyśmy podejść do tego problemu na jeden z dwóch sposobów. Problem klasyfikacji (gdzie sieć neuronowa przewiduje, czy piksel należy do klasy „niebieskiej” czy „szarej”, biorąc pod uwagę jego współrzędne xy) lub problem regresji (gdzie sieć neuronowa przewiduje wartości RGB dla piksela, biorąc pod uwagę jego współrzędne).
jeśli potraktujesz to jako problem regresji: wyniki treningu będą miały 3 wartości (znormalizowane wartości r, g, b dla każdego piksela). – Użyjmy tej metody na razie.
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
r,g,b = rgb
training_outputs.append((r/255,g/255,b/255))
teraz stwórzmy naszą ANN:

- powinien mieć 2 neurony w warstwie wejściowej (ponieważ są 2 wartości do przyjęcia: x& współrzędne y).
- powinien mieć 3 neurony w warstwie wyjściowej (ponieważ są 3 wartości do nauczenia: r, g, b).
- liczba ukrytych warstw i liczba neuronów w każdej ukrytej warstwie to dwa hiperparametry do eksperymentowania (jak również liczba epok, dla których będziemy ją trenować, funkcja aktywacji itp.) — użyję 10 ukrytych warstw ze 100 neuronami w każdej ukrytej warstwie (co czyni z tego głęboką sieć neuronową)
from sklearn.neural_network import MLPRegressorann = MLPRegressor(hidden_layer_sizes= tuple(100 for _ in range(10)))ann.fit(training_inputs, training_outputs)
wyszkolona sieć może teraz przewidzieć znormalizowane wartości rgb dla dowolnej warstwy. współrzędne (np. X,Y = 1,1).
ann.predict(])
array (])
pozwala używać ANN do przewidywania wartości RGB dla każdej współrzędnej i pozwala wyświetlić przewidywane wartości rgb dla całego obrazu, aby zobaczyć, jak dobrze się sprawdził (jakościowo — zostawimy metryki oceny dla innego samouczka)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
r,g,b = predicted_outputs
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

spróbuj zmienić hiperparametry, aby uzyskać lepsze wyniki.
Jeśli zamiast traktować to jako problem regresji, traktujemy to jako problem klasyfikacji, To wyniki treningu będą miały 2 wartości (prawdopodobieństwo piksela należącego do każdej z dwóch klas: „blue” i „grey”)
training_inputs,training_outputs = ,
for row,rgbs in enumerate(image_array):
for column,rgb in enumerate(rgbs):
training_inputs.append((row,column))
if sum(rgb) <= 600:
label = (0,1) #blue class
else:
label = (1,0) #grey class
training_outputs.append(label)
możemy odbudować naszą ANN jako klasyfikator binarny z 2 neuronami w warstwie wejściowej, 2 neuronami w warstwie wyjściowej i 100 neuronami w warstwie ukrytej (z 10 ukrytymi warstwami)
from sklearn.neural_network import MLPClassifier
ann = MLPClassifier(hidden_layer_sizes= tuple(100 for _ in range(10)))
ann.fit(training_inputs, training_outputs)
możemy teraz użyć wytrenowanej ann do przewidzenia klasy, do której należy każdy piksel (0: „szary” lub 1: „Niebieski”). The argmax function is used to find which class has the highest probability
np.argmax(ann.predict(]))
(this indicates the pixel with xy-coordinates 1,1 is most likely from class 0: „grey”)
predicted_outputs = ann.predict(training_inputs)predicted_image_array = np.zeros_like(image_array)
i = 0
for row,rgbs in enumerate(predicted_image_array):
for column in range(len(rgbs)):
prediction = np.argmax(predicted_outputs)
if prediction == 0:
predicted_image_array =
else:
predicted_image_array =
i += 1
Image.fromarray(predicted_image_array)

