w praktyce machine I deep learning parametry modelu są właściwościami danych treningowych, które będą uczyć się samodzielnie podczas treningu przez klasyfikator lub inny model ML. Na przykład, wagi i uprzedzenia, lub podzielić punkty w drzewie decyzji.
Hiperparametry modelu są zamiast tego właściwościami, które rządzą całym procesem treningowym. Obejmują one zmienne, które określają strukturę sieci (na przykład liczbę ukrytych jednostek) oraz zmienne, które określają sposób szkolenia sieci (na przykład szybkość uczenia się). Hiperparametry modelowe ustawiane są przed treningiem (przed optymalizacją ciężarów i biasu).
na przykład, oto niektóre wbudowane zmienne konfiguracyjne modelu :
- szybkość uczenia się
- liczba epok
- ukryte warstwy
- Ukryte jednostki
- aktywacje funkcje
Hiperparametry są ważne, ponieważ bezpośrednio kontrolują zachowanie algo treningowego, mając istotny wpływ na wydajność modelu w trakcie treningu.
wybór odpowiednich hiperparametrów odgrywa kluczową rolę w sukcesie architektur sieci neuronowych, biorąc pod uwagę wpływ na poznany model. Na przykład, jeśli wskaźnik uczenia się jest zbyt niski, model ominie ważne wzorce w danych; odwrotnie, jeśli jest wysoki, może mieć kolizje.
wybór dobrych hiperparametrów zapewnia dwie główne korzyści:
- efektywne wyszukiwanie w przestrzeni możliwych hiperparametrów; i
- łatwiejsze zarządzanie dużym zestawem eksperymentów do strojenia hiperparametrów.
Hiperparametry można z grubsza podzielić na 2 kategorie:
1. Hiperparametry optymalizatora,
2. Hiperparametry specyficzne dla Modelu
są one bardziej związane z procesem optymalizacji i szkolenia.
1.1. Wskaźnik uczenia się:
Jeśli wskaźnik uczenia się modelu jest zbyt mniejszy niż wartości optymalne, osiągnięcie idealnego stanu zajmie znacznie więcej czasu (setki lub tysiące) epok. Z drugiej strony, jeśli szybkość uczenia się jest znacznie większa niż wartość optymalna, to przekroczyłaby stan idealny i algorytm może się nie zbiegać. Rozsądny początkowy wskaźnik uczenia = 0,001.
ważne, aby wziąć pod uwagę, że:
a) model będzie miał setki i tysiące parametrów, każdy z własną krzywą błędów.
b) krzywe błędów nie są czystymi u-kształtami; zamiast tego mają tendencję do bardziej złożonych kształtów z lokalnymi minimami.
1.2. Mini-Wielkość Partii:
wielkość partii ma wpływ na zapotrzebowanie na zasoby procesu szkoleniowego, szybkość i liczbę iteracji w nietrywialny sposób.
historycznie dyskutowano o szkoleniu stochastycznym, w którym dopasowuje się jeden przykład zestawu danych do modelu i, używając tylko jednego przykładu, wykonuje przejście do przodu, oblicza błąd/backpropagate& ustawia skorygowane wartości dla wszystkich hiperparametrów. Następnie zrób to ponownie dla każdego przykładu w zbiorze danych.
lub, być może, lepiej przekazać całe dane do etapu szkolenia i obliczyć gradient za pomocą błędu generowanego przez przeglądanie wszystkich przykładów w zbiorze danych. To się nazywa trening wsadowy.
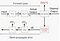
obecnie powszechnie stosowaną techniką jest ustawienie wielkości mini partii. Trening stochastyczny jest wtedy , gdy rozmiar Mini-batch =1, A Trening wsadowy jest wtedy, gdy rozmiar Mini-batch = liczba przykładów w zestawie treningowym. Zalecane wartości początkowe do eksperymentów: 1, 2, 4, 8, 16, 32, 64, 128, 256.
większy rozmiar mini-partii pozwala na zwiększenie obliczeniowe, które wykorzystuje mnożenie macierzy w obliczeniach treningowych . Jednak chodzi kosztem konieczności więcej pamięci dla procesu szkolenia. Mniejszy rozmiar mini-partii powoduje większy hałas w obliczeniach błędów, często bardziej przydatny w zapobieganiu zatrzymywaniu się procesu szkolenia na lokalnych minimach. Wartość godziwa dla wielkości mini partii= 32.
tak więc, podczas gdy obliczeniowy boost napędza nas do zwiększenia rozmiaru mini-partii, ta praktyczna korzyść algorytmiczna zachęca do faktycznego zmniejszenia.
1.3. Liczba epok:
aby wybrać odpowiednią liczbę epok dla etapu szkolenia, metryką, na którą powinniśmy zwrócić uwagę, jest błąd walidacji.
intuicyjny, ręczny sposób polega na tym, że model pociągu ma tyle iteracji, ile błędów walidacji maleje.
istnieje technika, której można użyć o nazwie Early stoping, aby określić, kiedy przerwać szkolenie modelu; chodzi o zatrzymanie procesu szkolenia w przypadku, gdy błąd walidacji nie poprawił się w ciągu ostatnich 10 lub 20 epok.
2. Hiperparametry Modelu
są one bardziej zaangażowane w strukturę Modelu:
2.1. Liczba ukrytych jednostek:
liczba ukrytych jednostek jest jednym z bardziej tajemniczych hiperparametrów. Pamiętajmy, że sieci neuronowe są uniwersalnymi aproksymatorami funkcji i aby mogły nauczyć się przybliżać funkcję (lub zadanie przewidywania) , muszą mieć wystarczającą „pojemność”, aby nauczyć się tej funkcji. Liczba ukrytych jednostek jest główną miarą zdolności uczenia się modelu.
dla prostej funkcji może potrzebować mniejszej liczby ukrytych jednostek. Im bardziej złożona funkcja, tym więcej zdolności uczenia się będzie potrzebował model.
nieco większa liczba jednostek niż liczba optymalna nie stanowi problemu, ale znacznie większa liczba doprowadzi do przepełnienia (tj. jeśli podasz model o zbyt dużej pojemności, może on mieć tendencję do przepełnienia, próbując „zapamiętać” zestaw danych, co wpływa na zdolność do uogólniania)
2.2. Pierwsza ukryta warstwa:
kolejna heurystyka obejmująca pierwszą warstwę ukrytą polega na tym, że ustawienie liczby ukrytych jednostek większej niż liczba wejść pozwala na lepsze wyniki w liczbie zadań, zgodnie z obserwacją empiryczną.
2.3. Liczba warstw:
często zdarza się, że 3-warstwowa sieć neuronowa przewyższy 2-warstwową. Ale zejście jeszcze głębiej rzadko pomaga o wiele bardziej. (wyjątkiem są Konwolucyjne Sieci neuronowe, gdzie im głębsze są, tym lepiej działają).
techniki optymalizacji Hiperparametrów
proces znajdowania najbardziej optymalnych hiperparametrów w uczeniu maszynowym nazywa się optymalizacją hiperparametrów.
typowe algorytmy obejmują:
- Wyszukiwanie Siatkowe
- Wyszukiwanie losowe
- Optymalizacja bayesowska
Wyszukiwanie Siatkowe
wyszukiwanie siatkowe jest tradycyjną techniką implementacji hiperparametrów. Jest to nieco o brute force wszystkie kombinacje. Wyszukiwanie siatki wymaga utworzenia dwóch zestawów hiperparametrów:
- szybkość uczenia się
- liczba warstw
Wyszukiwanie Siatkowe trenuje algorytm dla wszystkich kombinacji za pomocą dwóch zestawów hiperparametrów (szybkość uczenia się i liczba warstw) i mierzy wydajność za pomocą techniki weryfikacji krzyżowej. Ta technika walidacji zapewnia, że wyszkolony model pobiera większość wzorców ze zbioru danych (jedna z najlepszych metod przeprowadzania walidacji za pomocą „K-Fold cross Validation”, która pomaga dostarczyć obszernych danych do szkolenia modelu i obszernych danych do walidacji).
metoda wyszukiwania siatki jest prostszym algorytmem w użyciu, ale cierpi, jeśli dane mają dużą przestrzeń wymiarową zwaną przekleństwem wymiarowości.
losowe Wyszukiwanie
losowo próbki przestrzeni wyszukiwania i ocenia zestawy z określonego rozkładu prawdopodobieństwa. Zamiast próbować sprawdzić wszystkie 100 000 próbek, na przykład, możemy sprawdzić 1000 losowych parametrów.
wadą korzystania z algorytmu wyszukiwania losowego jest jednak to, że nie wykorzystuje informacji z wcześniejszych eksperymentów do wyboru następnego zestawu. Co więcej, trudno jest przewidzieć następny z eksperymentów.

optymalizacja Bayesa
ustawienie hiperparametru maksymalizuje wydajność modelu na zestawie walidacyjnym. Ml algos często wymaga dostrojenia hiperparametrów modelowych. Niestety, strojenie to często nazywa się „funkcją czarną”, ponieważ nie można go zapisać do wzoru (pochodne funkcji są nieznane).
bardziej atrakcyjny sposób optymalizacji& precyzyjne hiperparametry pociąga za sobą włączenie automatycznego podejścia do strojenia modelu-na przykład za pomocą optymalizacji bayesowskiej. Model używany do przybliżania funkcji celu nazywa się modelem zastępczym. Popularnym modelem zastępczym dla optymalizacji Bayesa jest proces Gaussa (GP). Optymalizacja bayesowska zazwyczaj działa poprzez założenie, że nieznana funkcja została pobrana z procesu Gaussa (GP) i utrzymuje tylny rozkład dla tej funkcji w miarę dokonywania obserwacji.
istnieją dwa główne wybory, które należy podjąć podczas wykonywania optymalizacji bayesowskiej:
- Wybierz wcześniej funkcje, które wyrażą założenia dotyczące funkcji optymalizowanej. W tym celu wybieramy najpierw proces Gaussa;
- następnie musimy wybrać funkcję akwizycji, która jest używana do konstruowania funkcji użytkowej z modelu tylnego, co pozwala nam określić następny punkt do oceny.
proces Gaussa
proces Gaussa definiuje wcześniejszy rozkład nad funkcjami, który można przekształcić w tylny nad funkcjami, gdy tylko zobaczymy jakieś dane. Proces Gaussa wykorzystuje macierz kowariancji, aby zapewnić, że wartości są blisko siebie. Macierz kowariancji wraz ze średnią funkcją µ do wyprowadzenia wartości oczekiwanej ƒ (x) definiuje proces Gaussa.
1. Proces Gaussa będzie użyty jako preform dla wnioskowania Bayesa;
2. Obliczenie tylnej umożliwia jej wykorzystanie do przewidywania niewidocznych przypadków testowych.

Acquisition Function
Introducing sampling data into the search space is done by acquisition functions. It helps to maximize the acquisition function to determine the next sampling point. Popularne funkcje akwizycji to
- maksymalne prawdopodobieństwo poprawy (MPI)
- oczekiwana poprawa (ei)
- górna granica ufności (UCB)
oczekiwana poprawa (ei) jest popularna i zdefiniowana jako:
EI(x)=𝔼
Gdzie ƒ(x ) jest bieżącym optymalnym zestawem hiperparametrów. Maksymalizacja hiperparametrów poprawi się po ƒ.
