bez nadzoru wnioskowanie Bayesa (zmniejszanie wymiarów i odkrywanie cech)
wykrywanie cech niskiego poziomu za pomocą krawędzi

wreszcie, moment, na który wszyscy czekaliście, następny w naszym bez nadzoru bayesowska seria wnioskowania: nasze (nie tak) głębokie zanurzenie w operatorze Sobela.
prawdziwie magiczny algorytm wykrywania krawędzi, umożliwia niskopoziomową ekstrakcję funkcji i redukcję wymiarowości, zasadniczo redukując szumy w obrazie. Jest szczególnie przydatny w aplikacjach do rozpoznawania twarzy.
ten algorytm, dziecko miłości Irwina Sobela i Gary ’ ego Feldmana (Stanford Artificial Intelligence Laboratory) z 1968 roku, był inspiracją dla wielu nowoczesnych technik wykrywania krawędzi. Przez zawijanie dwóch przeciwstawnych jąder lub masek nad danym obrazem (np. patrz niżej-po lewej) (każdy zdolny do wykrywania poziomych lub pionowych krawędzi), możemy stworzyć mniej hałaśliwą, wygładzoną reprezentację (patrz poniżej-po prawej).
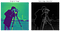
Presented as a discrete differential operator technique for gradient approximation computation of the image intensity function, in plain English, the algorithm detects changes in pixel channel wartości (Zwykle luminancja) poprzez różnicowanie różnicy między każdym pikselem (piksel kotwicy) a otaczającymi go pikselami (zasadniczo przybliżając pochodną obrazu).
powoduje to wygładzenie oryginalnego obrazu i uzyskanie niższego wymiaru, gdzie niskopoziomowe cechy geometryczne mogą być wyraźniej widoczne. Wyjścia te mogą być następnie wykorzystane jako wejścia do bardziej złożonych algorytmów klasyfikacji lub jako przykłady używane do nienadzorowanego grupowania probabilistycznego za pomocą dywergencji Kullbacka-Leiblera (KLD) (jak widać na moim niedawnym blogu na LBP).
generowanie wyjścia o niższym wymiarze wymaga od nas wzięcia pochodnej obrazu. Najpierw obliczamy pochodną w kierunku x i Y. Tworzymy dwa jądra 3×3 (patrz macierze), z zerami wzdłuż środka odpowiedniej osi, dwójkami w środku kwadratów prostopadłych do centralnego zera i jedynkami w każdym z rogów. Każda z niezerowych wartości powinna być dodatnia na górze / na prawo od zer (w zależności od osi) i ujemna na odpowiadającej im stronie. Jądra te noszą nazwy Gx i Gy.
pojawiają się one w formacie:
te jądra będą się wtedy obracać nad naszym obrazem, umieszczając centralny piksel każdego jądra nad każdym pikselem obrazu. Używamy mnożenia macierzy do obliczenia wartości intensywności nowego odpowiadającego piksela w obrazie wyjściowym, dla każdego jądra. W związku z tym otrzymujemy dwa obrazy wyjściowe (po jednym dla każdego kierunku kartezjańskiego).
celem jest znalezienie różnicy/zmiany między pikselem na obrazie a wszystkimi pikselami w macierzy gradientowej (jądrze) (Gx i Gy). Bardziej matematycznie można to wyrazić jako.
notka boczna:
technicznie niczego nie zawijamy. Chociaż lubimy odnosić się do „splotów” w kręgach sztucznej inteligencji i uczenia maszynowego, sploty polegałyby na odwróceniu oryginalnego obrazu. Matematycznie mówiąc, Kiedy mówimy o splotach, naprawdę obliczamy korelację krzyżową między każdym obszarem 3×3 wejścia i maską dla każdego piksela. Obraz wyjściowy jest ogólną kowariancją między maską a wejściem. W ten sposób wykrywane są krawędzie.
powrót do naszego wyjaśnienia Sobel…
obliczone wartości dla każdego mnożenia macierzy między maską a sekcją 3×3 wejścia są sumowane, aby uzyskać końcową wartość piksela na obrazie wyjściowym. Generuje to nowy obraz, który zawiera informacje o obecności pionowych i poziomych krawędzi obecnych w oryginalnym obrazie. Jest to geometryczna reprezentacja cech oryginalnego obrazu. Ponadto, ponieważ operator ten jest gwarantowany do produkcji tego samego wyjścia za każdym razem, technika ta pozwala na stabilne wykrywanie krawędzi Dla zadań segmentacji obrazu.
na podstawie tych wyników możemy obliczyć zarówno wielkość gradientu, jak i kierunek gradientu (przy użyciu operatora arctangent) dla dowolnego piksela (x,y):
Z to możemy stwierdzić, że te piksele o dużych powiększeniach są bardziej prawdopodobne, aby być krawędzią obrazu, podczas gdy kierunek informuje nas o orientacji krawędzi (chociaż kierunek nie jest potrzebny do generowania naszego wyjścia).
prosta implementacja:
oto prosta implementacja operatora Sobel w Pythonie (używającego NumPy), aby dać ci odczucie procesu (dla wszystkich początkujących programistów).
Ta implementacja jest pythonową odmianą pseudokodu Wikipedii, mającą na celu pokazanie, w jaki sposób można zaimplementować ten algorytm, jednocześnie demonstrując różne etapy procesu.
Dlaczego nas to obchodzi?
chociaż aproksymacja gradientu wytwarzana przez ten operator jest stosunkowo surowa, zapewnia niezwykle wydajną obliczeniowo metodę obliczania krawędzi, narożników i innych geometrycznych cech obrazów. Z kolei utorowało to drogę dla wielu technik redukcji wymiarowości i ekstrakcji cech, takich jak lokalne wzorce binarne (zobacz mój inny blog, aby uzyskać więcej informacji na temat tej techniki).
opierając się wyłącznie na cechach geometrycznych istnieje ryzyko utraty ważnych informacji podczas kodowania naszych danych, jednak kompromis jest tym, co pozwala na szybkie wstępne przetwarzanie danych, a co za tym idzie, szybkie szkolenie. Dlatego ta technika jest szczególnie przydatna w scenariuszach, w których tekstury i cechy geometryczne mogą być uważane za bardzo ważne w definiowaniu danych wejściowych. Dlatego też rozpoznawanie twarzy można wykonać ze stosunkowo dużą dokładnością za pomocą operatora Sobel. Jednak technika ta może nie być najlepszym wyborem w przypadku próby klasyfikacji lub grupowania danych wejściowych, które wykorzystują Kolor Jako główny czynnik różnicujący.
metoda ta jest nadal niezwykle skuteczna w uzyskiwaniu niskowymiarowej reprezentacji cech geometrycznych i doskonałym punktem wyjścia dla wymiarowości i redukcji szumów, przed zastosowaniem innych klasyfikatorów lub do zastosowania w metodach wnioskowania bayesowskiego.