Opublikowany czerwiec 2008.
druga z dwóch kolumn o matematyce Geodezji (pierwsza jest tutaj). …
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
Uniwersytet Kalifornijski w San Diego
jeggers na ucsd.edu
 Wyślij wiadomość do znajomego Wyślij wiadomość do znajomego |
 wydrukuj ten artykuł wydrukuj ten artykuł |
planimetr jest przyrządem stołowym do pomiaru obszarów, Zwykle obszarów nieregularnych na mapie lub zdjęciu. Były one kiedyś powszechne, ale obecnie w dużej mierze zostały zastąpione przez narzędzia cyfrowe.
poniższy obrazek daje pewne wyobrażenie o konfiguracji. Ramię słupa obraca się swobodnie wokół słupa, który jest zamocowany na stole. Ramię tracer obraca się wokół sworznia, gdzie łączy się z ramieniem biegunowym. Śledzisz krzywą w kierunku zgodnym z ruchem wskazówek zegara za pomocą znacznika, a w ten sposób koło pomiarowe toczy się wzdłuż, a całkowita odległość toczenia jest gromadzona na tarczy. Koło podporowe zapobiega przewróceniu się rzeczy. Na koniec odczytujemy liczbę z tarczy i po pomnożeniu przez współczynnik zależny tylko od konkretnej konfiguracji planimetru otrzymujemy pole wewnątrz krzywej.

następna cyfra daje lepszy widok na mechanizm.

wózek nazywamy zespołem kół, pokrętłem i obrotem. Na następnym zdjęciu lepiej się temu przyjrzysz i zobaczysz napęd robaka, który powoduje obracanie pokrętła podczas ruchu koła pomiarowego.

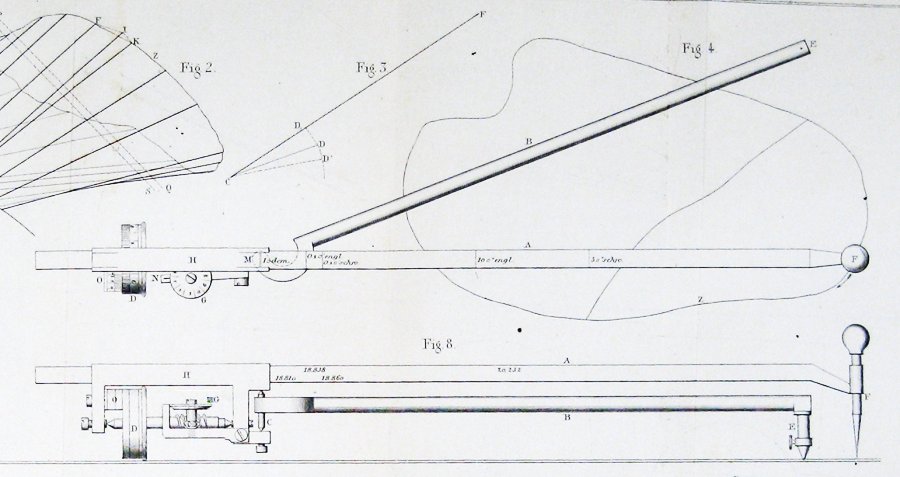
oto schemat oryginalnego planimetru z artykułu Jakoba Amslera, który go wprowadził:
jak taka prosta rzecz może mierzyć obszary?
Geometria planimetru
ruch zgodnie z ruchem wskazówek zegara planimetru jest kierunkiem przeciwnym do tego, co matematycy uznali za dodatni obrót. Zamiast łamać tę konwencję, od teraz będziemy pracować z planimetrem matematycznym, w którym poruszamy się w kierunku przeciwnym do ruchu wskazówek zegara. Podobnie jak fantazje innych matematyków, nie ma ich na tej planecie!
istnieją pewne ograniczenia dotyczące sposobu umieszczania planimetru w odniesieniu do krzywej, którą chcesz prześledzić. Wózek może być przesuwany wzdłuż ramienia znacznika, ale we wszystkich przypadkach Długość L ramienia znacznika jest mniejsza niż długość r ramienia słupka. Oznacza to, że znacznik nigdy nie może dostać się w odległości r – l od bieguna. Z drugiej strony, gdy jest całkowicie rozciągnięty, znacznik nigdy nie może sięgać poza r + l. Tak więc krzywa, którą należy prześledzić, musi leżeć w pierścieniu między dwoma okręgami, jednym o promieniu r-l, drugim r + l.

w rzeczywistości za chwilę powinno stać się jasne, że ramiona nigdy nie powinny być całkowicie wysunięte, więc wyznaczona krzywa musi leżeć całkowicie wewnątrz pierścienia. Ponadto, zwykle biegun jest umieszczony na zewnątrz krzywej.

dla danego punktu pierścienia istnieją dokładnie dwie możliwe konfiguracje planimetru, które umieszczają znacznik w tym punkcie. Wybór jednego punktu lub drugiego oznacza wybór znaku dla pierwiastka kwadratowego. Nazywamy to wyborem orientacji dla planimetru. Jest dodatnia, jeśli pierwiastek kwadratowy jest dodatni. Po wybraniu orientacji pozostaje ona taka sama, chyba że ramię jest całkowicie wysunięte. To nie może się zdarzyć. Tak długo, jak krzywa jest całkowicie w pierścieniu, konfiguracje planimetru będą się zmieniać płynnie i wyjątkowo w zależności od ścieżki znacznika.
następną rzeczą do zrobienia jest zrozumienie kilku rzeczy na temat ruchu koła pomiarowego. Jak pokazuje poniższy rysunek, jeśli koło porusza się po linii prostej a odległość C, koło obraca się o kąt θ = c/r, gdzie R jest jego promieniem.

więc prawdą jest, że obrót koła i odległość pokonana przez ramię Tracera mają ze sobą jakiś związek. Ale ten związek jest nieco subtelny. Jeśli ramię przesunie się prosto o odległość C, obszar wyrzucony będzie lC, ale jeśli przesunie się równolegle do siebie, obszar wyrzucony będzie równy 0. W pierwszym przypadku punkt na obwodzie koła przesunie się o odległość C. w drugim przypadku koło w ogóle się nie poruszy. A jeśli ramię przekłada się ukośnie, koło obraca się o odległość równą wysokości równoległoboku pokrytego ramieniem. We wszystkich przypadkach, gdy ramię przekłada się równolegle do siebie, obszar wyparty przez część ramienia znacznika między czopem a znacznikiem będzie równy lC, gdzie C jest odległością zmierzoną przez obrót koła. Jest to podstawowy fakt związany z ruchem ramienia z ruchem koła pomiarowego.

sposób wyrażenia tego precyzyjnie jest taki, że bez względu na to, jak porusza się ramię, odległość mierzona przez koło jest ścieżką integralną

gdzie Γ jest ścieżką pokonywaną przez punkt ramienia, w którym jest przymocowane koło pomiarowe, n jest wektorem jednostkowym prostopadłym do ramienia w dowolnym momencie, A T jest wektorem jednostkowym skierowanym w kierunku jazdy (tak, że np. jeśli ramię porusza się równolegle do siebie iloczyn punktowy n i T wynosi 0).
twierdzenie Guldina
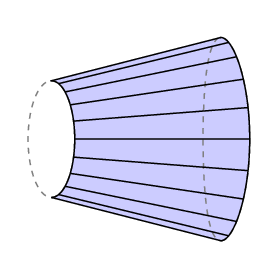
następnie spróbujemy wyjaśnić intuicyjnie zachowanie planimetru, ale najpierw przyjrzymy się specjalnemu rodzajowi planimetru i w tym przypadku udowodnimy bardziej ogólny wynik. Załóżmy, że weźmiemy jedno swobodnie poruszające się ramię o długości l i przymocujemy do niego koło pomiarowe o promieniu R w jego środku.

następnie przesuwamy ramię w płaszczyźnie. Jeśli koło pomiarowe obraca się o całkowity kąt θ radianów, gdy ramię porusza się wokół, odległość punktu na obwodzie wynosi C = θR.
twierdzenie Guldina. W tej sytuacji całkowity obszar wyparty przez ramię jest produktem lC.
obszar tutaj interpretowany jest znakiem. Jeśli ramię obraca się wokół środka, jedna połowa ramienia idzie do przodu, a druga do tyłu, a te dwa się anulują.
przekonaliśmy się już, że twierdzenie Guldina jest słuszne w przypadku, gdy ramię właśnie się tłumaczy. Oczywiście nie zawsze tak się dzieje – ramię może się obracać podczas ruchu, a także przekładać. Ale możemy zobaczyć, co się dzieje, siekając obszar zamiatany w następujący sposób:

ponieważ koło pomiarowe znajduje się na środku ramienia, gdy ramię obraca się, zgniata małe bloki z jednej strony, gdy rozszerza je z drugiej. Te efekty dokładnie się znoszą.
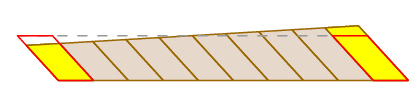
całkowicie rygorystyczny dowód można podać za pomocą wzoru na zmianę zmiennych w podwójnej całce i wyrażenia na przesunięcie koła jako całki ścieżki.
Załóżmy, że koło jest umieszczone gdzie indziej. Powiedzmy, że jego pozycja to c + v, gdzie c jest środkiem ramienia, a v wektorem wzdłuż ramienia. Długość v pozostanie stała, powiedzmy w ρ. Ścieżka, którą podąża koło, to c(t) + v (T). Całka ścieżki jest teraz
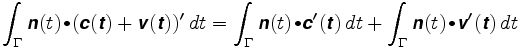
pierwszą całką jest odległość, jaką przemierzyłoby koło, gdyby znajdowało się na środku ramienia. W drugim wektor v(t) jest zawsze prostopadły do n, A v(t) ma stałą długość. Wektor v (t) porusza się po okręgu o promieniu równym ρ. Zatem iloczyn punktowy N I v '(t) jest po prostu długością znakową v'(t), a druga Całka jest równa ρ razy całkowity obrót ramienia. Stąd:
Jeśli koło znajduje się w odległości ρ od środka ramienia, odległość C , którą mierzy koło, wynosi C0, odległość, która byłaby mierzona, gdyby koło znajdowało się w środku, plus ρ razy całkowity kąt θ, który obraca ramię.
możesz od razu zobaczyć jeden prosty przypadek, obracając ramię wokół jego środka. Łącząc to z twierdzeniem Guldina, widzimy, że we wszystkich przypadkach:
c = C0 + ρ θ
Area swept out = l C0 = l C – L ρ θ
pełny wynik
formuła Guldina daje obszar podpisany – jeśli zamiatasz do tyłu nad obszarem, koło się cofnie i anulujesz obszar, który już pokryłeś. Jeśli zastosujemy to do przypadku, w którym wolne ramię wraca dokładnie do miejsca, w którym się zaczęło, widzimy, że lC jest równe obszarowi obszaru zamkniętego wyznaczonemu przez prawy koniec ramienia minus obszarowi wymazanemu przez lewy.

w przypadku planimetru biegunowego dno ramienia jest ograniczone do łuku okręgu o promieniu r ze środkiem na biegunie, stąd l C jest obszarem namierzony przez nadajnik. Ponadto, normalnie biegun leży poza obszarem, który ma być mierzony, i w tym przypadku całkowita ilość obrotów ramienia musi wynosić 0. Tak więc w tym przypadku mamy
Area of the region traced = lC
oto liczba zawarta przez Jakoba Amslera, wynalazcę, w jego oryginalnej pracy na temat instrumentu, który wynalazł:
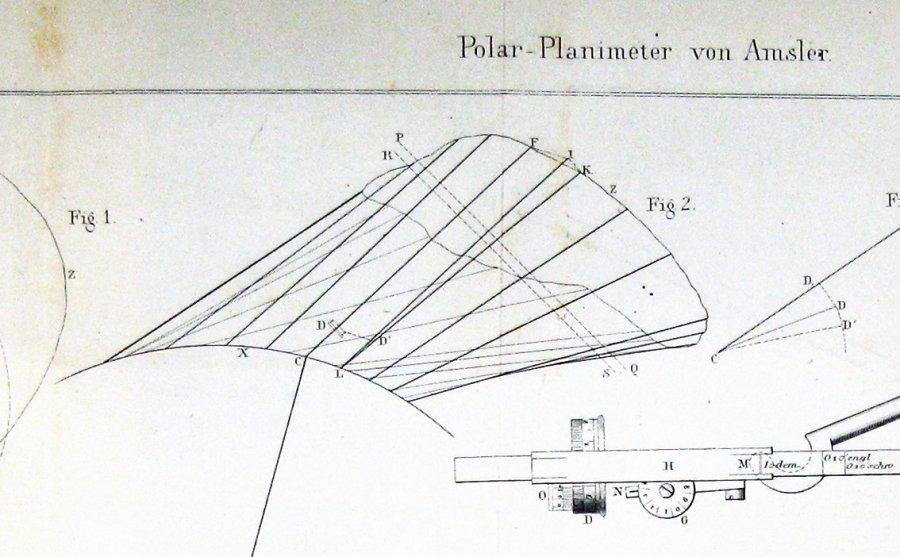
wydaje się całkiem jasne z tego, że Amsler wyprowadził swoją konstrukcję za pomocą jakiejś formy twierdzenia Guldina.
Planimetry i twierdzenie Greena
jak już wspomnieliśmy, po wybraniu orientacji planimetru konfiguracja planimetru jest ciągłą funkcją położenia znacznika. Powiedzmy, że wybieramy pozytywną orientację. Następnie możemy dołączyć do każdego punktu pierścienia wektor jednostkowy n, ten skierowany przeciwnie do ruchu wskazówek zegara i prostopadły do ramienia znacznika na znaczniku.
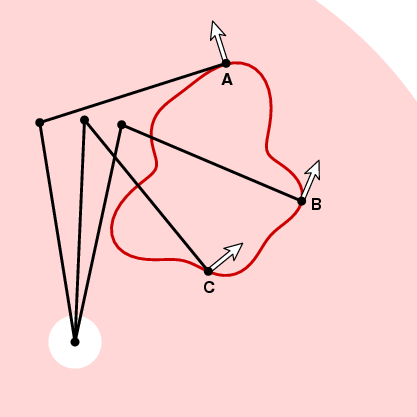
sposób reakcji koła pomiarowego na ruch wzdłuż krzywej w następnej chwili zależy od kąta między tym wektorem a jednostkowym wektorem stycznym krzywej. Na powyższym obrazku koło pomiarowe nie będzie się poruszać, ponieważ ruch wzdłuż krzywej jest równoległy do ramienia znacznika. W punkcie B jeśli znacznik przesunie się o niewielką odległość, tak samo koło pomiarowe. A w C koło pomiarowe przesunie się o pewną odległość między 0 a ds. Aby być dokładnym, Załóżmy, że t jest jednostkowym wektorem stycznym w pewnym punkcie krzywej. Jeśli znacznik przesunie odległość DS wzdłuż krzywej, w tym punkcie koło pomiarowe przesunie odległość D ds, gdzie d = N. t, iloczyn punktowy wektorów jednostkowych t i N. innymi słowy, jeśli poruszamy się po krzywej Γ, koło pomiarowe przesunie się o całkowitą odległość równą całce z N. t DS (iloczyn kropkowy), lub

ale ponieważ każdy punkt pierścienia odpowiada unikalnej dodatniej konfiguracji planimetru, możemy przypisać wektor n do każdego wewnętrznego punktu pierścienia, a zatem definiuje on pole wektorowe. Krzywa Γ jest granicą jej wnętrza Ω i według jednego z naszych założeń mieści się ona w całości w obszarze, w którym zdefiniowano N. Twierdzenie Greena mówi nam, że Całka ścieżki wokół granicy tego obszaru jest również równa pewnej całce nad Ω: Dlatego
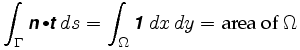
dokładniej, twierdzenie Greena mówi nam, że
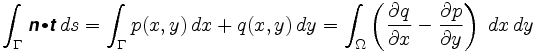
gdzie n = jest polem wektorowym. Całka w całce podwójnej nazywana jest zwinięciem pola wektorowego.
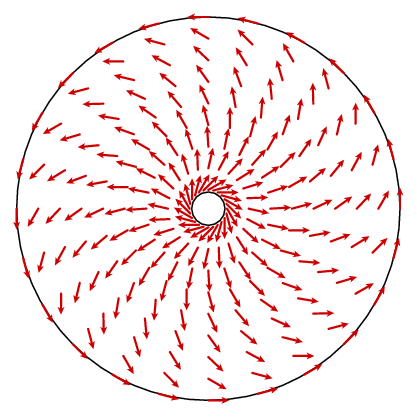
Powinno się zdarzyć, że zwinięcie jest stałą 1. W zasadzie możemy znaleźć wzór na pole wektorowe n i obliczyć jego zwijanie, ale to nie jest zbyt pouczające. Możemy jednak skorzystać z innego faktu. Pole wektorowe ma symetrię kołową, co oznacza, że jest określone przez to, co znajduje się na jednym promieniu. Prawo cosinusa daje nam prosty wzór na składnik obwodowy.
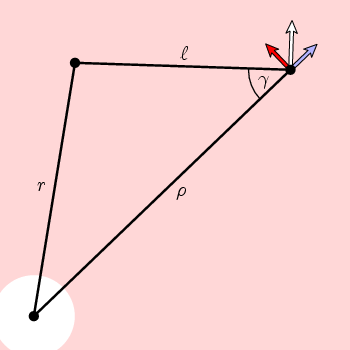
z prostej geometrii na tym rysunku wynika, że obwodową składową N jest
f(ρ) = cos(γ) = (ρ 2 + L 2 – R 2)/(2 ρ l)
rzeczywisty punkt twierdzenia Greena polega na tym, że aby zweryfikować, czy liczba całkowita wynosi 1, wystarczy zweryfikować, czy Całka ścieżki wokół odpowiedniej małej ścieżki są takie same jak obszar. W tym celu wybieramy nasze regiony tak, jak tutaj:
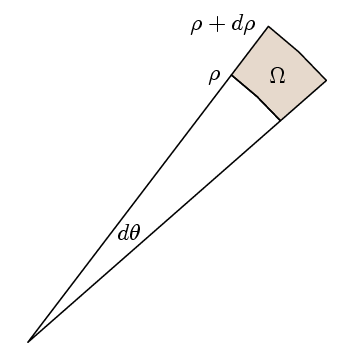
wtedy l razy Całka ścieżki wynosi
l (ρ+dp)( f(ρ+dp)- f(ρ) ) dθ
lub
(θ/2) ( (ρ + dp) 2 – ρ 2)
co jest obszarem regionu Ω.
inne rodzaje planimetrów
twierdzenie Guldina zakłada, że ruch koła pomiarowego powie Ci obszar wyśledzony przez znacznik, gdy ramię z kołem pomiarowym na nim wyśledzi krzywą, ale ma jeden koniec ograniczony do krzywej jednowymiarowej. Dzieje się tak na przykład w przypadku planimetru tocznego, w którym czop jest ograniczony do linii prostej przez położenie na walcu tocznym.

aby dowiedzieć się więcej
-
 nadal produkuje i sprzedaje planimetry.
nadal produkuje i sprzedaje planimetry. - Rachunek różniczkowy i całkowy Tom II, R. Courant, Blackie & syn, 1936. Rozdział o wzorze Guldina (S. 294-298) zawiera wyjaśnienie, jak działa planimetr.
- oryginalny artykuł Amslera, Vierteljahresschrift der Naturforschenden Gesellschaft in Zuerich, 1856. Tutaj brakuje diagramów, ale są one tutaj:
- pierwszy diagram Amslera
- drugi diagram Amslera
dziękujemy Donnie Sammis z Biblioteki Uniwersytetu Stony Brook za zlokalizowanie artykułu i jej mężowi Robertowi za dostarczenie zdjęć figur.
firma założona przez Amslera produkowała Instrumenty jeszcze w XX wieku. To zdjęcie przedstawia logo na pantografowej wersji planimetru:

- „o Planimetrach”, Inżynierowie. Firma opublikowała również film na YouTube.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
John Eggers
University of California, San Diego
jeggers at ucsd.edu
ci, którzy mają dostęp do JSTOR, mogą znaleźć tam niektóre z wyżej wymienionych dokumentów. Dla tych, którzy mają dostęp, program MathSciNet Amerykańskiego Towarzystwa Matematycznego może być wykorzystany do uzyskania dodatkowych informacji bibliograficznych i recenzji niektórych z tych materiałów. Niektóre z powyższych pozycji można uzyskać za pośrednictwem portalu ACM, który zapewnia również usługi bibliograficzne.