Uczenie się bez nadzoru funkcji i głębokie uczenie się Tutorial

wprowadzenie

analiza głównych komponentów (PCA) to algorytm redukcji wymiarowości, który może być użyty do znacznego przyspieszenia algorytmu uczenia się bez nadzoru funkcji. Co ważniejsze, zrozumienie PCA pozwoli nam później wdrożyć wybielanie, które jest ważnym etapem wstępnego przetwarzania dla wielu algorytmów.

Załóżmy, że trenujesz swój algorytm na obrazkach. Wtedy Dane wejściowe będą nieco zbędne, ponieważ wartości sąsiednich pikseli w obrazie są silnie skorelowane. Konkretnie, Załóżmy, że trenujemy na łatach obrazów w skali szarości 16×16. Wtedy \textstyle x\in \ Re^{256} są 256 wektorami wymiarowymi, z jedną cechą \textstyle x_j odpowiadającą intensywności każdego piksela. Ze względu na korelację między sąsiednimi pikselami, PCA pozwoli nam przybliżyć dane wejściowe o znacznie niższym wymiarze, przynosząc bardzo mały błąd.

przykład i tło Matematyczne

w naszym uruchomionym przykładzie użyjemy zbioru danych \textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\} z \textstyle n=2 wejściami wymiarowymi, tak że \textstyle x^{(i)} \in \Re^2. Załóżmy, że chcemy zmniejszyć dane z 2 wymiarów do 1. (W praktyce możemy chcieć zredukować dane z 256 do 50 wymiarów, powiedzmy; ale użycie danych o niższych wymiarach w naszym przykładzie pozwala nam lepiej wizualizować algorytmy.) Oto nasz zbiór danych:

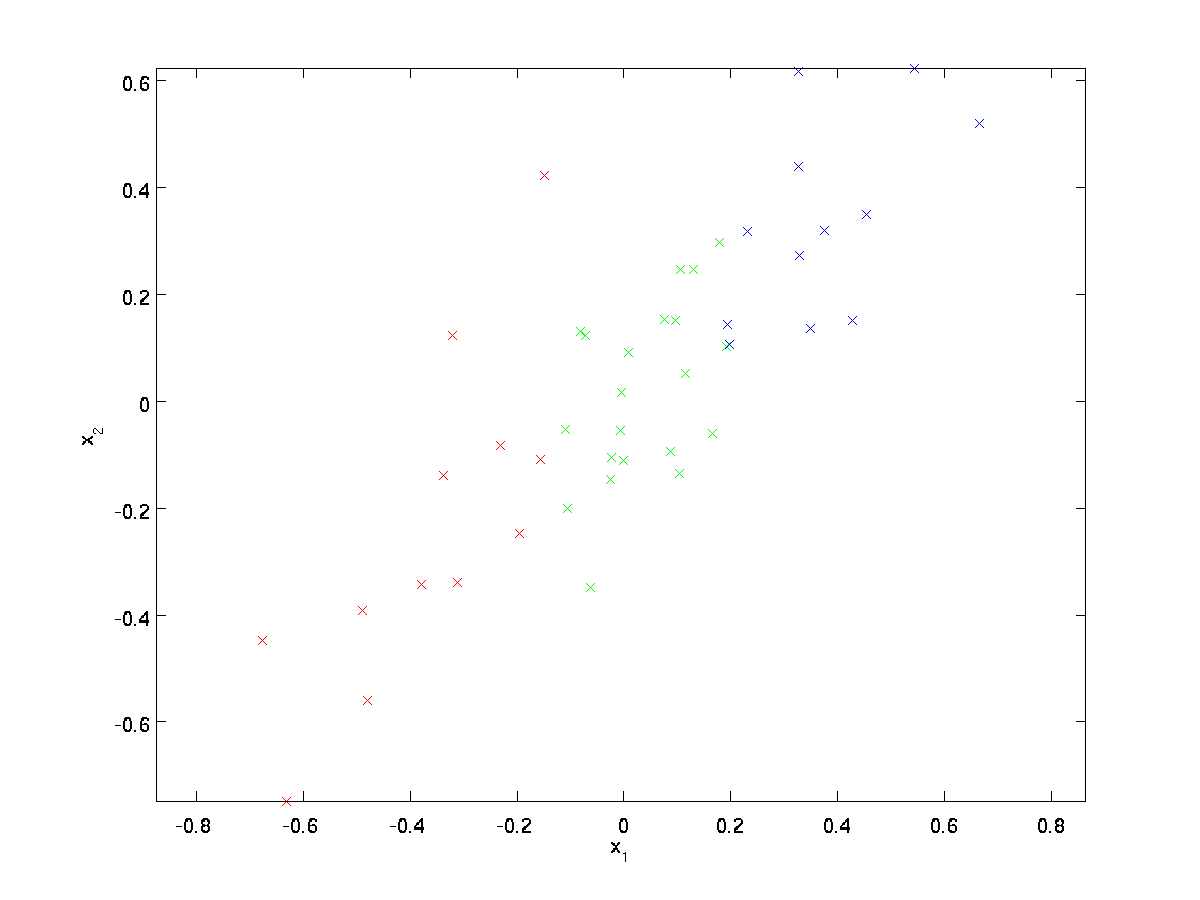
te dane zostały już wstępnie przetworzone tak, że każda z funkcji \textstyle x_1 i \textstyle x_2 ma mniej więcej taką samą średnią (zero) i wariancję.

dla celów ilustracji, również pokolorowaliśmy każdy z punktów jednym z trzech kolorów, w zależności od ich wartości \ textstyle x_1; kolory te nie są używane przez algorytm i służą jedynie do ilustracji.

PCA znajdzie podprzestrzeń o niższym wymiarze, na której będą wyświetlane nasze dane.
Z wizualnego badania danych wynika, że \textstyle u_1 jest głównym kierunkiem zmienności danych, a \textstyle u_2 wtórnym kierunkiem zmienności:

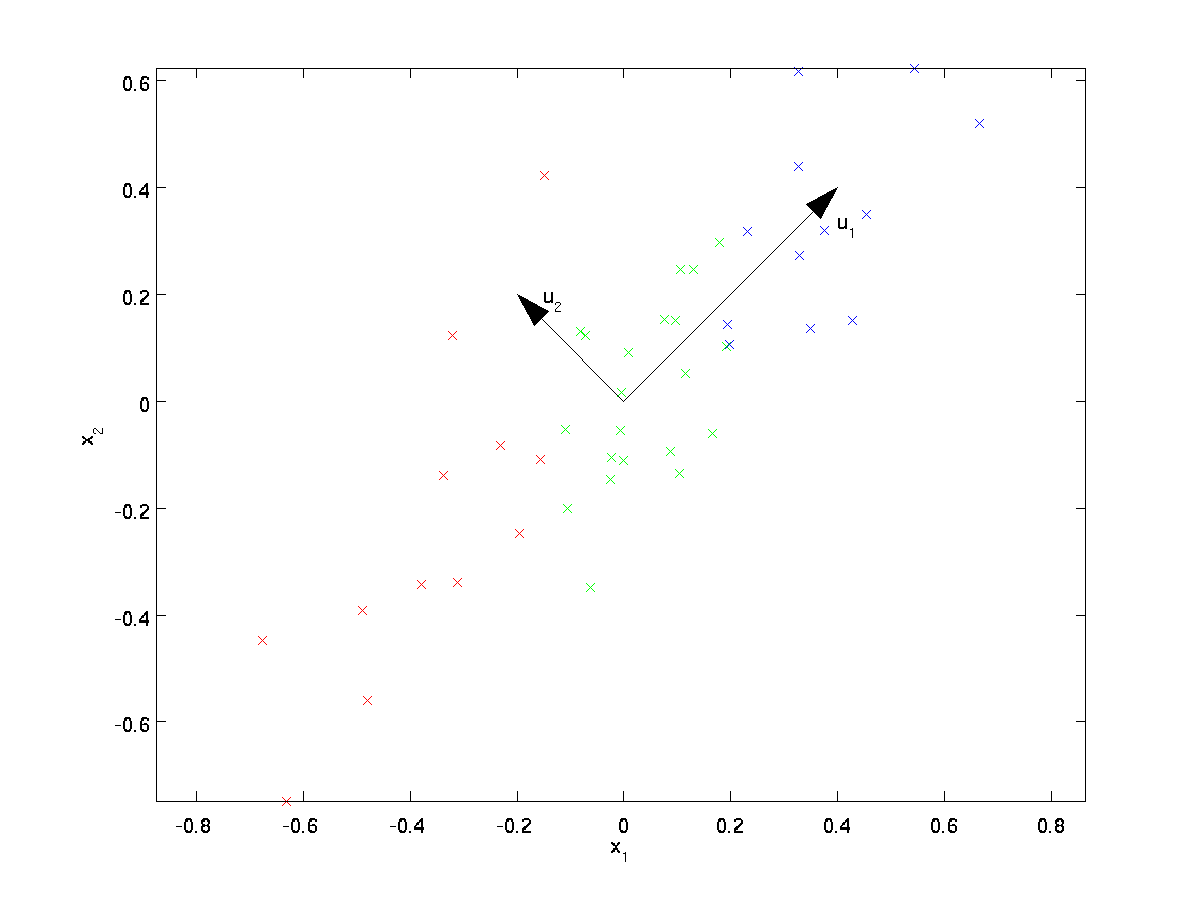
tzn. dane różnią się znacznie bardziej w kierunku \textstyle u_1 niż \textstyle u_2. Aby bardziej formalnie znaleźć kierunki \textstyle u_1 i \ textstyle u_2, najpierw obliczamy macierz \ textstyle \ Sigma w następujący sposób:

\ begin{align} \ Sigma = \ frac{1}{m} \sum_ {i = 1}^m (x^{(i)}) (x^{(i)})^T. \end{align}

Jeśli \textstyle X ma średnią zerową, to \textstyle \ Sigma jest dokładnie macierzą kowariancji \textstyle x. (symbol „\textstyle \Sigma”, wymawiane „Sigma”, jest standardową notacją oznaczającą macierz kowariancji. Niestety wygląda jak symbol sumowania, jak w \sum_{i = 1}^N i; ale to są dwie różne rzeczy.)

można wtedy pokazać, że \textstyle u_1—główny kierunek zmienności danych—jest górnym (głównym) wektorem własnym \textstyle \Sigma, a \textstyle u_2 jest drugim wektorem własnym.

Uwaga: Jeśli jesteś zainteresowany bardziej formalną derywacją matematyczną / uzasadnieniem tego wyniku, Zobacz notatki z wykładu CS229 (Machine Learning) na temat PCA (link na dole tej strony). Nie musisz tego robić, aby podążać tym kursem.

Możesz użyć standardowego oprogramowania do numerycznej algebry liniowej, aby znaleźć te wektory własne (zobacz Uwagi dotyczące implementacji). Konkretnie, obliczmy wektory własne \textstyle \ Sigma i ułożymy je w kolumnach, tworząc macierz \ textstyle U:

\begin{align}U = \begin{bmatrix} | &&& | \\u_1 & u_2 & \cdots & u_n \\| &&& | \end{bmatrix} \end{align}

Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), \textstyle u_2 is the second eigenvector, and so on. Also, let \textstyle\lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.

wektory \textstyle u_1 i \textstyle u_2 w naszym przykładzie tworzą nową podstawę, w której możemy reprezentować dane. Konkretnie, niech \textstyle x \in \ Re^2 będzie przykładem treningu. Wtedy \textstyle u_1^Tx jest długością (wielkością) rzutu \textstyle x na wektor \textstyle u_1.

podobnie \textstyle u_2^Tx jest wielkością \textstyle x rzutowaną na wektor \textstyle u_2.

obracanie danych

w ten sposób możemy reprezentować \textstyle x w \textstyle (u_1, u_2)-na podstawie obliczeń

\begin{align}x_{\RM rot} = u^Tx = \begin{bmatrix} u_1^TX \\ u_2^TX \end{bmatrix} \end{align}

(indeks dolny „rot” pochodzi z obserwacji, że odpowiada to obrotowi (i ewentualnie odbicie) oryginalnych danych.) Weźmy cały zestaw treningowy i obliczmy \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} dla każdego \textstyle i. wykreślając te przekształcone dane \textstyle x_{\RM rot}, otrzymamy:

jest to zestaw treningowy zamieniony na \textstyle u_1,\textstyle u_2. W ogólnym przypadku \textstyle U^Tx będzie zestawem treningowym obracanym do bazy \ textstyle u_1,\textstyle u_2,…, \textstyle u_n.

jedną z właściwości \textstyle u jest to, że jest to macierz „ortogonalna”, co oznacza, że spełnia \textstyle U^TU = UU^T = I. Więc jeśli kiedykolwiek trzeba przejść z obróconych wektorów \textstyle x_{\rm rot} z powrotem do oryginalnych danych \textstyle x, można obliczyć

\begin{align}x = U x_{\RM rot} ,\end{align}

ponieważ \textstyle U x_{\RM rot} = uu^t X = x.

zmniejszając wymiar danych

widzimy,że głównym kierunkiem zmienności danych jest pierwszy wymiar \textstyle x_{\RM rot, 1} tych obróconych danych. Tak więc, jeśli chcemy zmniejszyć te dane do jednego wymiaru, możemy ustawić

\begin{align}\tilde{x}^{(i)} = x_ {\RM rot,1}^{(i)} = u_1^Tx^{(i)} \in \ Re.\ end{align}

bardziej ogólnie, jeśli \textstyle x \in \ Re^n i chcemy go zredukować do \ textstyle K reprezentacji wymiarowej \textstyle \ tylda{x} \in \ Re^k (gdzie k < n), weźmiemy pierwsze \textstyle K składniki \textstyle x_ {\rm rot}, które odpowiadają górnym \ textstyle K Kierunki wariacji.

innym sposobem wyjaśnienia PCA jest to, że \textstyle x_{\RMVB} jest \textstyle n wektorem wymiarowym, gdzie pierwsze kilka elementów może być dużych (np. w naszym przykładzie zobaczyliśmy, że \textstyle x_ {\RM rot, 1}^{(i)} = u_1^Tx^{(i)} przyjmuje dość duże wartości dla większości przykładów \textstyle i), a późniejsze komponenty są prawdopodobnie małe (np. w naszym przykładzie \textstyle x_{\RM rot, 2}^{(i)} = u_2^Tx^{(i)} było bardziej prawdopodobne,że małe). Co robi PCA to zrzuca późniejsze (mniejsze) komponenty \textstyle x_{\rm rot} i tylko przybliża je zerami. konkretnie, nasza definicja \textstyle \tylda{x} może być również osiągnięta przy użyciu przybliżenia do \textstyle x_{\RM rot} gdzie wszystkie oprócz pierwszych \textstyle K komponenty są zerami. Innymi słowy, mamy:

\begin{align}\tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\\vdots \\ x_{\RM rot,k} \\0 \\ \vdots \\ 0 \\ \end{bmatrix}\approx \begin{bmatrix} x_{\RM rot,1} \\\vdots \\ x_{\RM rot,k} \\x_{\RM rot,K+1} \\\vdots \\ x_{\RM rot,N} \end{bmatrix}= x_{\RM rot} \end{align}

w naszym przykładzie daje nam to następujący wykres \textstyle \tylda{x} (używając \textstyle N=2, K=1):

jednak, ponieważ końcowe \textstyle n-k składowe \textstyle \tylda{x} jak zdefiniowano powyżej zawsze będzie równe zero, nie ma potrzeby trzymania tych zer wokół, dlatego definiujemy \textstyle \tylda{x} jako \textstyle K-wymiarowy wektor z tylko pierwszymi \textstyle K (niezerowymi) składowymi.

to również wyjaśnia, dlaczego chcieliśmy wyrazić nasze dane w podstawie \textstyle u_1, u_2, \ldots, u_n: decydowanie, które komponenty zachować, staje się po prostu utrzymaniem górnych \textstyle k komponentów. Kiedy to robimy, mówimy również, że ” zachowujemy górne \textstyle K PCA (lub główne) składniki.”

Odzyskiwanie aproksymacji danych

teraz, \textstyle \ tylda{x} \ in \ Re^k jest niskowymiarową,” skompresowaną ” reprezentacją oryginalnego \textstyle x \in \Re^n. biorąc pod uwagę \textstyle \tylda{x}, jak możemy odzyskać aproksymację \textstyle \hat{x} do pierwotnej wartości \textstyle x? Z wcześniejszej sekcji wiemy, że \textstyle x = U x_{\RMVB}. Dalej, możemy myśleć o \textstyle \tylda{x} jako o przybliżeniu do\textstyle x_ {\RMVB}, gdzie ustawiliśmy Ostatnie \ textstyle n-k składowe na zera. Tak więc, biorąc pod uwagę \textstyle \tilde{x} \in \Re^k, możemy wyprowadzić go z \textstyle n-k zera, aby uzyskać nasze przybliżenie do \textstyle x_{\rm rot} \in \Re^N. na koniec, wstępnie mnożymy przez \textstyle U, aby uzyskać nasze przybliżenie do \textstyle x. konkretnie, otrzymujemy

\begin{align}\hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^K u_i \tilde{x}_i. \end{align}

ostateczna równość powyżej pochodzi z definicji \textstyle u podanej wcześniej. (W praktycznej implementacji, nie będziemy w rzeczywistości zerować pad \textstyle \tylda{x}, a następnie pomnożyć przez \textstyle U, ponieważ oznaczałoby to mnożenie wielu rzeczy przez zera; zamiast tego, po prostu pomnożylibyśmy \textstyle \tylda{x} \w \Re^K z pierwszymi \textstyle K kolumnami \textstyle U, jak w ostatnim wyrażeniu powyżej.) Stosując to do naszego zbioru danych, otrzymujemy następujący wykres dla \textstyle \hat{x}:

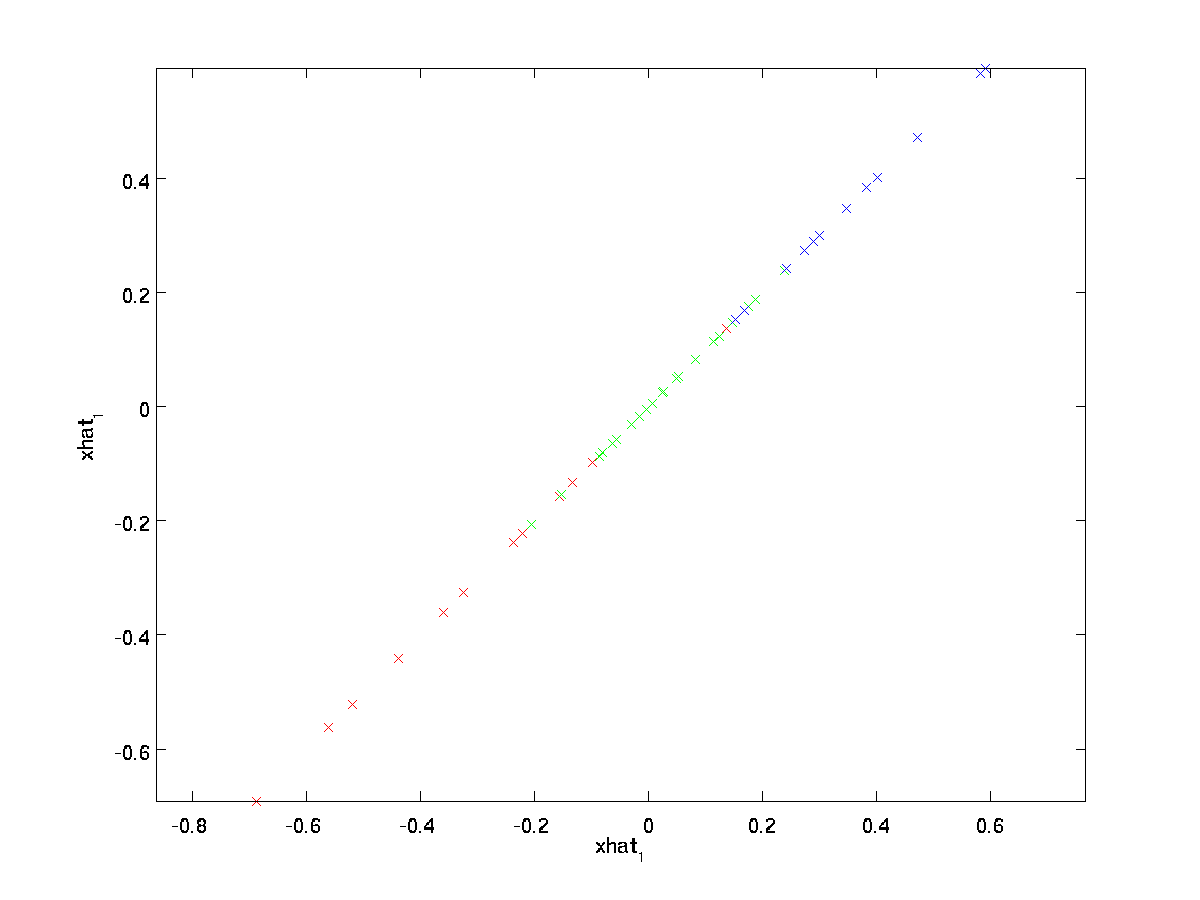
używamy więc 1-wymiarowego przybliżenia do oryginalnego zbioru danych.

jeśli trenujesz autoencoder lub inny algorytm uczenia funkcji bez nadzoru, czas działania Twojego algorytmu będzie zależał od wymiaru danych wejściowych. Jeśli podasz \textstyle \ tilde{x} \ in \ Re^k do swojego algorytmu nauki zamiast \textstyle x, będziesz trenować na niższym wymiarze, a zatem Twój algorytm może działać znacznie szybciej. Dla wielu zbiorów danych, niższa reprezentacja \ textstyle \ tilde{x} może być bardzo dobrym przybliżeniem do oryginału, a użycie PCA w ten sposób może znacznie przyspieszyć algorytm, wprowadzając bardzo mały błąd przybliżenia.

Ilość komponentów do zachowania

Jak ustawić \textstyle k, czyli ile komponentów PCA powinniśmy zachować? W naszym prostym dwuwymiarowym przykładzie naturalne wydawało się zachowanie 1 z 2 składników, ale dla danych o wyższych wymiarach ta decyzja jest mniej trywialna. Jeśli \textstyle k jest zbyt duży, to nie będziemy kompresować danych za bardzo; w granicy \textstyle k = n, to używamy tylko oryginalnych danych (ale obróconych w inną podstawę). Odwrotnie, jeśli \textstyle k jest zbyt mały, to możemy używać bardzo złego przybliżenia danych.

aby zdecydować, jak ustawić \textstyle k, Zwykle przyjrzymy się”’ procent zachowanej wariancji „’ dla różnych wartości \textstyle K. konkretnie, jeśli \textstyle k=n, mamy dokładne przybliżenie do danych i mówimy, że 100% wariancji jest zachowana. Tj., wszystkie zmiany oryginalnych danych są zachowywane. I odwrotnie, jeśli \textstyle k = 0, to przybliżamy wszystkie dane z wektorem zerowym, a zatem zachowujemy 0% wariancji.

bardziej ogólnie, niech \textstyle \ lambda_1, \ lambda_2, \ ldots, \lambda_n będą wartościami własnymi \textstyle \ Sigma (posortowane w kolejności malejącej), tak że \textstyle \lambda_j jest wartością własną odpowiadającą wektorowi własnemu \ textstyle u_j. wtedy jeśli zachowamy \ textstyle K główne składniki, procent zachowanej wariancji jest podany przez:

\begin{align}\frac{\sum_{j=1}^k \lambda_j}{\sum_{j = 1}^n \lambda_j}.\end{align}

w naszym prostym przykładzie 2D powyżej, \textstyle \lambda_1 = 7.29 i \textstyle \lambda_2 = 0.69. Tak więc, zachowując tylko \ textstyle K=1 Główne składniki, zachowaliśmy \textstyle 7.29/(7.29+0.69) = 0.913, lub 91,3% wariancji.

bardziej formalna definicja procentu zachowanej wariancji wykracza poza zakres tych uwag. Można jednak pokazać, że \textstyle \lambda_j = \ sum_{i=1}^m x_{\rm, j}^2. Tak więc, jeśli \textstyle \ lambda_j \ approx 0, to pokazuje, że \textstyle x_ {\RMVB, j} i tak jest zwykle blisko 0, a tracimy stosunkowo niewiele przez przybliżenie go stałą 0. Wyjaśnia to również, dlaczego zachowujemy górne główne komponenty (odpowiadające większym wartościom \textstyle \lambda_j) zamiast dolnych. Główne składowe \textstyle x_{\Rmx,j} to te, które są bardziej zmienne i przyjmują większe wartości, i dla których spowodowalibyśmy większy błąd aproksymacji, gdybyśmy ustawili je na zero.

w przypadku obrazów, jedną z powszechnych heurystyk jest wybranie \textstyle k tak, aby zachować 99% wariancji. Innymi słowy, wybieramy najmniejszą wartość \textstyle k, która spełnia

\begin{align}\frac {\sum_{j=1}^k\lambda_j} {\sum_{j=1}^n \lambda_j} \ geq 0.99. \end{align}

w zależności od aplikacji, Jeśli chcesz ponieść dodatkowy błąd, czasami używane są również wartości z zakresu 90-98%. Kiedy opisujesz innym, jak zastosowałeś PCA, powiedzenie, że wybrałeś \textstyle k, aby zachować 95% wariancji, będzie również znacznie łatwiejszym opisem interpretowalnym niż powiedzenie, że zachowałeś 120 (lub dowolną inną liczbę) komponentów.

PCA na obrazkach

aby PCA działało, zwykle chcemy, aby każda z funkcji \textstyle x_1, x_2, \ldots, x_n miała podobny zakres wartości do innych (i miała średnią bliską zeru). Jeśli wcześniej korzystałeś z PCA w innych aplikacjach, możesz oddzielnie przetwarzać każdą funkcję, aby miała średnią zerową i wariancję jednostkową, oddzielnie szacując średnią i wariancję każdej funkcji \textstyle x_j. jednak nie jest to wstępne przetwarzanie, które zastosujemy do większości typów obrazów. W szczególności, Załóżmy, że trenujemy nasz algorytm na „’obrazy naturalne”’, tak że \textstyle x_j jest wartością piksela \textstyle j. przez” obrazy naturalne ” nieformalnie rozumiemy typ obrazu, który typowe zwierzę lub osoba może zobaczyć w ciągu swojego życia.

Uwaga: Zazwyczaj używamy obrazów scen plenerowych z trawą, drzewami itp., i wyciąć małe (powiedzmy 16×16) łaty obrazu losowo z nich trenować algorytm. Ale w praktyce większość algorytmów uczenia się funkcji jest niezwykle odporna na dokładny typ obrazu, na którym jest szkolona, więc większość zdjęć wykonanych normalnym aparatem, o ile nie są zbyt rozmyte lub mają dziwne artefakty, powinna działać.

podczas treningu na naturalnych obrazach nie ma sensu szacować osobnej średniej i wariancji dla każdego piksela, ponieważ statystyki w jednej części obrazu powinny (teoretycznie) być takie same jak w każdej innej.
ta właściwość obrazów nazywa się „’stationarity.”’

w szczegółach, aby PCA działało dobrze, nieformalnie wymagamy, aby (i) cechy miały w przybliżeniu średnią zerową, a (ii) różne cechy miały podobne różnice do siebie. Przy naturalnych obrazach (ii) jest już spełniony nawet bez normalizacji wariancji, więc nie będziemy wykonywać żadnej normalizacji wariancji.
(jeśli trenujesz na danych dźwiękowych-np. na spektrogramach-lub na danych tekstowych-np. na wektorach workowych – zwykle nie przeprowadzamy normalizacji wariancji.)
W rzeczywistości PCA jest niezmienny w stosunku do skalowania danych i zwróci te same wektory własne niezależnie od skalowania danych wejściowych. Bardziej formalnie, jeśli pomnożysz każdy wektor funkcji \ styl tekstu x przez pewną liczbę dodatnią (skalując w ten sposób każdą funkcję w każdym przykładzie treningowym o tę samą liczbę), wyjściowe wektory własne PCA Nie ulegną zmianie.

więc nie będziemy używać normalizacji wariancji. Jedyną normalizacją, którą musimy wykonać, jest normalizacja średnia, aby zapewnić, że cechy mają średnią około zera. W zależności od zastosowania Bardzo często nie interesuje nas, jak jasny jest ogólny obraz wejściowy. Na przykład w zadaniach rozpoznawania obiektów ogólna jasność obrazu nie wpływa na obiekty znajdujące się na obrazie. Bardziej formalnie, nie jesteśmy zainteresowani średnią wartością intensywności plastra obrazu; w ten sposób możemy odjąć tę wartość, jako formę średniej normalizacji.

konkretnie, jeśli \textstyle x^{(i)} \in \Re^{n} są wartościami intensywności (w skali szarości) łaty obrazu 16×16 (\textstyle n=256), możemy normalizować intensywność każdego obrazu \textstyle X^{(i)} w następujący sposób:

\mu^{(i)} := \frac{1}{n} \sum_{j=1}^N X^{(i)}_jx^{(i)}_j := x^{(i)}_j – \mu^{(i)}

dla wszystkich \textstyle j

zauważ, że dwa powyższe kroki są wykonywane oddzielnie dla każdego obrazu \textstyle x^{(i)}, a to \textstyle \mu^{(i)} tutaj jest średnia intensywność obrazu \textstyle X^{(i)}. W szczególności nie jest to to samo, co Szacowanie wartości średniej oddzielnie dla każdego piksela \ stylu tekstu x_j.

jeśli trenujesz swój algorytm na obrazach innych niż obrazy naturalne (na przykład obrazy znaków odręcznych lub obrazy pojedynczych izolowanych obiektów wyśrodkowanych na białym tle), inne rodzaje normalizacji mogą być warte rozważenia, a najlepszym wyborem może być zależny od aplikacji. Ale podczas treningu na naturalnych obrazach, użycie metody normalizacji średniej na obraz, jak podano w powyższych równaniach, byłoby rozsądnym błędem.

wybielanie

użyliśmy PCA do zmniejszenia wymiarów danych. Istnieje ściśle powiązany etap wstępnego przetwarzania zwany wybielaniem (lub, w niektórych innych literaturach, sfering), który jest potrzebny dla niektórych algorytmów. Jeśli ćwiczymy na obrazach, surowe dane wejściowe są zbędne, ponieważ wartości sąsiednich pikseli są silnie skorelowane. Celem wybielania jest uczynienie danych wejściowych mniej zbędnymi; bardziej formalnie, nasze desiderata polega na tym, że nasze algorytmy uczące się widzą dane wejściowe szkoleniowe, w których (i) cechy są mniej skorelowane ze sobą i (ii) Wszystkie cechy mają tę samą wariancję.

przykład 2D

najpierw opiszemy wybielanie używając naszego poprzedniego przykładu 2D. Następnie opiszemy, jak można to połączyć z wygładzaniem, a na koniec, jak połączyć to z PCA.

Jak możemy sprawić, że nasze funkcje wejściowe będą nieskorelowane ze sobą? Zrobiliśmy to już przy obliczaniu \textstyle x_{\rm}^{(i)} = U^Tx^{(i)}.
powtarzając naszą poprzednią figurę, nasz wykres dla \textstyle x_{\RMVB} wynosił:

macierz kowariancji tych danych jest podana przez:

\begin{align}\begin{bmatrix}7.29 && 0.69\end{bmatrix}.\ end{align}

(Uwaga: Technicznie, wiele stwierdzeń w tej sekcji o „kowariancji” będzie prawdziwe tylko wtedy, gdy dane mają średnią zerową. W dalszej części tej sekcji przyjmiemy to założenie jako ukryte w naszych wypowiedziach. Jednak nawet jeśli średnia danych nie jest dokładnie zerowa, intuicje, które tutaj prezentujemy, nadal są prawdziwe, więc nie jest to coś, o co powinieneś się martwić.)

to nie przypadek, że wartości przekątnej to \textstyle \lambda_1 i \textstyle \lambda_2. Co więcej, pozycje poza przekątną są zerowe; zatem \textstyle x_ {\rm rot, 1} i \textstyle x_{\RM rot, 2} są nieskorelowane, spełniając jedną z naszych dezyderat dla wybielonych danych (aby cechy były mniej skorelowane).

aby każda z naszych funkcji wejściowych miała wariancję jednostkową, możemy po prostu przeskalować każdą funkcję \textstyle x_{\rm rot,i} przez \textstyle 1/\sqrt{\lambda_i}. Konkretnie definiujemy nasze wybielone dane \textstyle x_{\RM PCAwhite} \ in \ Re^n w następujący sposób:

\ begin{align}x_ {\RM PCAwhite, i} = \ frac{x_ {\RM rot, i}} {\sqrt {\lambda_i}}. \end{align}

\ textstyle x_ {\RMVB}, otrzymujemy:

te dane mają teraz kowariancję równą macierzy tożsamości \textstyle I. mówimy, że \textstyle x_{\RM PCAwhite} jest naszą wybieloną wersją danych PCA: różne składniki \textstyle x_{\RM PCAwhite} są nieskorelowane i mają wariancję jednostkową.

wybielanie połączone z redukcją wymiarów. Jeśli chcesz mieć dane, które są wybielone i które są mniej wymiarowe niż oryginalne wejście, możesz również opcjonalnie zachować tylko górne \textstyle K składniki \textstyle x_ {\RM PCAwhite}. Gdy połączymy wybielanie PCA z regularyzacją (opisaną później), to kilka ostatnich elementów \textstyle x_{\RM PCAwhite} i tak będzie prawie zerowe, a zatem można bezpiecznie zrezygnować.

wybielanie ZCA

W końcu okazuje się, że ten sposób uzyskiwania danych do kovariance identity \textstyle I nie jest unikalny. Konkretnie, jeśli \textstyle R jest dowolną macierzą ortogonalną, tak że spełnia \textstyle RR^T = R^TR = I ( mniej formalnie, jeśli \textstyle R jest macierzą obrotu / odbicia), to \textstyle R \, x_{\rm} będzie również mieć kowariancję tożsamości.

w wybielaniu ZCA wybieramy \textstyle R = U. definiujemy

\begin{align}x_{\RM Zcawhite} = U x_{\RM PCAwhite}\end{align}

Wykreślamy \textstyle x_{\RM ZCAwhite}, otrzymujemy:

It można pokazać, że spośród wszystkich możliwych opcji dla \textstyle r, ten wybór rotacji powoduje, że \textstyle x_{\RM zcawhite} jest jak najbardziej zbliżony do oryginalnych danych wejściowych \textstyle x.

podczas korzystania z wybielania zca (w przeciwieństwie do wybielania PCA), Zwykle zachowujemy wszystkie \textstyle n wymiary danych i nie staramy się zmniejszać ich wymiarów.

Regularyzaton

podczas implementacji wybielania PCA lub zca w praktyce, czasami niektóre wartości własne \textstyle \lambda_i będą numerycznie zbliżone do 0, a zatem krok skalowania, w którym dzielimy przez \sqrt{\lambda_i} wymagałby podzielenia przez wartość bliską zeru; może to spowodować, że dane zostaną powiększone (przyjmą duże wartości) lub w inny sposób będą numerycznie niestabilne. Dlatego w praktyce wykonujemy ten krok skalowania przy użyciu niewielkiej ilości regularyzacji i dodajemy małą stałą \textstyle \ epsilon do wartości własnych przed wzięciem ich pierwiastka kwadratowego i odwrotnością:

\ begin{align} x_{\Rmx, i} = \ frac{x_ {\Rmx, i}} {\sqrt{\lambda_i + \ epsilon}}.\end{align}

gdy \textstyle x przyjmuje wartości wokół \textstyle , typowa może być wartość \textstyle \epsilon \approx 10^{-5}.

w przypadku obrazów dodanie \textstyle \epsilon ma również efekt lekko wygładzenia (lub filtrowania dolnoprzepustowego) obrazu wejściowego. Ma to również pożądany efekt usuwania artefaktów aliasingu spowodowanych sposobem ułożenia pikseli na obrazie i może poprawić poznane funkcje (szczegóły są poza zakresem tych notatek).

wybielanie ZCA jest formą wstępnego przetwarzania danych, które mapuje je z \textstyle X do \textstyle x_{\rm ZCAwhite}. Okazuje się, że jest to również szorstki model tego, jak oko biologiczne (siatkówka) przetwarza obrazy. W szczególności, gdy twoje oko postrzega obrazy, większość sąsiednich „pikseli” w twoim oku będzie postrzegać bardzo podobne wartości, ponieważ sąsiednie części obrazu są zwykle silnie skorelowane pod względem intensywności. Jest więc marnotrawstwem dla oka, aby przesłać każdy piksel osobno (przez nerw wzrokowy) do mózgu. Zamiast tego, twoja siatkówka wykonuje operację dekorrelacji (odbywa się to za pomocą neuronów siatkówki, które obliczają funkcję o nazwie „on center, off surround/off center, on surround”), która jest podobna do tej wykonywanej przez ZCA. Powoduje to mniej nadmiarową reprezentację obrazu wejściowego, który jest następnie przesyłany do mózgu.

implementacja wybielania PCA

w tej sekcji podsumowujemy algorytmy wybielania PCA, PCA i zca, a także opisujemy, w jaki sposób można je zaimplementować za pomocą wydajnych bibliotek algebry liniowej.

Po pierwsze, musimy upewnić się, że dane mają (w przybliżeniu) średnią zerową. W przypadku naturalnych obrazów osiągamy to (w przybliżeniu) poprzez odjęcie średniej wartości każdej łatki obrazu.

osiągamy to obliczając średnią dla każdej łatki i odejmując ją dla każdej łatki. W Matlabie możemy to zrobić używając

 avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. x = x - repmat(avg, size(x, 1), 1);

następnie musimy obliczyć \textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. jeśli implementujesz to w Matlabie (lub nawet jeśli implementujesz to w C++, Javie, itp., ale mają dostęp do wydajnej biblioteki algebry liniowej), robienie tego jako jawnej sumy jest nieefektywne. Zamiast tego możemy obliczyć to za jednym zamachem jako

 sigma = x * x' / size(x, 2);

(Sprawdź poprawność matematyki.) Zakładamy, że X jest strukturą danych, która zawiera jeden przykład treningowy na kolumnę (tak więc X jest macierzą \textstyle n-by-\textstyle m).

następnie PCA oblicza wektory własne \Sigma. Można to zrobić za pomocą funkcji Matlab eig. Ponieważ jednak \ Sigma jest symetryczną dodatnią macierzą półprzezroczystą, jest to bardziej niezawodne numerycznie przy użyciu funkcji svd. Konkretnie, jeśli zaimplementujesz

 = svd(sigma);

to macierz U będzie zawierała wektory własne \Sigma (jeden wektor własny na kolumnę, posortowany w kolejności od góry do dołu), a ukośne wpisy macierzy s będą zawierały odpowiednie wartości własne (również posortowane w kolejności malejącej). Macierz V będzie równa U i może być bezpiecznie zignorowana.

(Uwaga: Funkcja svd oblicza wektory liczby pojedynczej i wartości liczby pojedynczej macierzy, która w szczególnym przypadku symetrycznej dodatniej macierzy półprzeznaczonej—co jest wszystkim, o co tu chodzi-jest równa jej wektorom własnym i wartościom własnym. Pełne omówienie wektorów pojedynczych a wektorów własnych wykracza poza zakres tych notatek.)

wreszcie, możesz obliczyć \textstyle x_{\rm rot} i \textstyle \tilde{x} w następujący sposób:

 xRot = U' * x; % rotated version of the data. xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, % where k is the number of eigenvectors to keep

to daje reprezentację PCA danych w kategoriach \textstyle \tilde{x} \in \Re^K. Nawiasem mówiąc, jeśli X jest macierzą \textstyle N-by-\textstyle m zawierającą wszystkie dane treningowe, jest to wektoryzowana implementacja, a powyższe wyrażenia działają również dla obliczenia x_{\rm rot} i \ tylda{x} dla całego zestawu treningowego za jednym zamachem. Wynikowe x_{\rm} i \ tylda{x} będą miały jedną kolumnę odpowiadającą każdemu przykładowi treningowemu.

aby obliczyć wybielone dane PCA \textstyle x_{\RM PCAwhite}, użyj

 xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

ponieważ przekątna S zawiera wartości własne \textstyle \lambda_i, okazuje się,że jest to kompaktowy sposób obliczania \textstyle x_{\RM PCAwhite,i} = \frac{x_{\RM rot, i} }{\sqrt{\lambda_i}} jednocześnie dla wszystkich \textstyle i.

wreszcie, możesz również obliczyć wybielone dane zca \textstyle x_{\RM zcawhite} jako:

 xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;