w tym tutorialu zanurkujemy w podstawy przepływu optycznego, przyjrzymy się niektórym jego zastosowaniom i zaimplementujemy jego dwa główne warianty (rzadki i gęsty). Krótko omówimy również nowsze podejścia wykorzystujące głębokie uczenie się i obiecujące przyszłe kierunki.
Ostatnie przełomy w badaniach wizji komputerowej pozwoliły maszynom postrzegać otaczający świat za pomocą takich technik, jak wykrywanie obiektów do wykrywania instancji obiektów należących do określonej klasy i segmentacja semantyczna do klasyfikacji pikseli.
jednak, do przetwarzania wejścia wideo w czasie rzeczywistym, większość implementacji tych technik adresuje tylko relacje obiektów w tej samej klatce \((x, y)\) z pominięciem informacji o czasie \((t)\). Innymi słowy, oceniają każdą klatkę niezależnie, tak jakby były to zupełnie niepowiązane obrazy, dla każdego przebiegu. Co jednak, jeśli potrzebujemy relacji między kolejnymi klatkami, na przykład chcemy śledzić ruch pojazdów w klatkach, aby oszacować jego aktualną prędkość i przewidzieć jego położenie w następnej klatce?
lub, alternatywnie, co zrobić, jeśli potrzebujemy informacji o ludzkich relacjach pozowania między kolejnymi klatkami, aby rozpoznać ludzkie działania, takie jak Łucznictwo, baseball i koszykówka?


w tym samouczku dowiemy się, czym jest przepływ optyczny, jak wdrożyć jego dwa główne warianty (rzadki i gęsty), a także uzyskać duży obraz nowszych podejść obejmujących głębokie uczenie się i obiecujące przyszłe kierunki.
Co To jest przepływ optyczny?
Implementing Sparse Optical Flow
Implementing Dense Optical Flow
Deep learning and beyond
- co to jest przepływ optyczny?
- oszczędny vs gęsty przepływ optyczny
- implementacja Sparse Optical Flow
- Konfigurowanie środowiska
- Konfigurowanie OpenCV do odczytu wideo i konfigurowanie parametrów
- Shi-Tomasi Corner Detector – wybieranie pikseli do śledzenia
- śledzenie konkretnych obiektów
- Lucas-Kanade: Sparse Optical Flow
- implementując gęsty przepływ optyczny
- Konfigurowanie środowiska
- Konfigurowanie OpenCV do odczytu wideo
- przepływ optyczny Farneback
- przepływ optyczny przy użyciu głębokiego uczenia
- zastosowanie przepływu optycznego: segmentacja semantyczna
- zastosowanie przepływu optycznego: wykrywanie obiektów& śledzenie
- wniosek
co to jest przepływ optyczny?
Zacznijmy od wysokiego poziomu zrozumienia przepływu optycznego. Przepływ optyczny to ruch obiektów między kolejnymi klatkami sekwencji, spowodowany względnym ruchem między obiektem a kamerą. Problem przepływu optycznego można wyrazić jako:
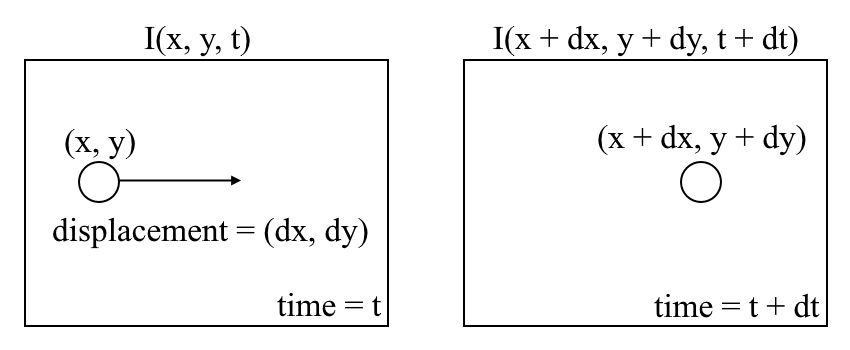
gdzie między kolejnymi klatkami możemy wyrazić intensywność obrazu \((I)\) jako funkcję spacji \((x, y)\) i czas \((t)\). Innymi słowy, jeśli weźmiemy pierwszy obrazek \(I (x, y, t)\) i przesuniemy jego piksele o \((dx, dy)\) nad \(t\) czasem, otrzymamy nowy obrazek \(I(x + dx, y + dy, t + dt)\).
Po pierwsze, Zakładamy, że intensywność pikseli obiektu jest stała między kolejnymi klatkami.
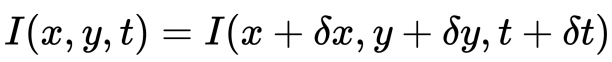
Po Drugie, bierzemy aproksymację szeregów Taylora RHS i usuwamy wspólne terminy.
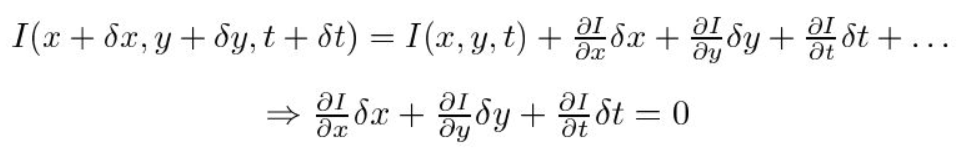
Po Trzecie, dzielimy przez \(dt\), aby uzyskać równanie przepływu optycznego:
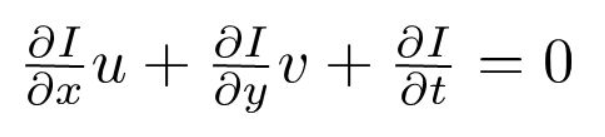
gdzie \(u = dx/DT\) i \(v = dy / dt\).
\(dI/DX, dI/dy\) i \(dI / DT\) to gradienty obrazu wzdłuż osi poziomej, osi pionowej i czasu. Stąd kończymy z problemem przepływu optycznego, czyli rozwiązaniem \(u (DX/dt)\) i \(v (dy/dt)\) w celu określenia ruchu w czasie. Możesz zauważyć, że nie możemy bezpośrednio rozwiązać równania przepływu optycznego dla \(u\) I \(v\), ponieważ istnieje tylko jedno równanie dla dwóch nieznanych zmiennych. Zaimplementujemy niektóre metody, takie jak metoda Lucas-Kanade, aby rozwiązać ten problem.
oszczędny vs gęsty przepływ optyczny
oszczędny przepływ optyczny daje wektorom przepływu pewne „interesujące cechy” (powiedzmy kilka pikseli obrazujących krawędzie lub rogi obiektu) w ramce, podczas gdy gęsty przepływ optyczny, który daje wektory przepływu całej ramki (wszystkie piksele) – do jednego wektora przepływu na piksel. Jak można się domyślić, gęsty przepływ optyczny ma wyższą dokładność kosztem powolnego / kosztownego obliczeniowo.
implementacja Sparse Optical Flow
Sparse optical flow wybiera niewielki zestaw funkcji pikseli (np. ciekawe funkcje, takie jak krawędzie i narożniki) do śledzenia jego wektorów prędkości (ruchu). Wyodrębnione funkcje są przekazywane w funkcji przepływu optycznego od klatki do klatki, aby zapewnić śledzenie tych samych punktów. Istnieją różne implementacje rzadkiego przepływu optycznego, w tym metoda Lucasa-Kanade, metoda Horna-Schuncka, metoda Buxtona–Buxtona i inne. Do implementacji będziemy używać metody Lucas-Kanade z OpenCV, otwartoźródłową biblioteką algorytmów wizji komputerowej.
Konfigurowanie środowiska
Jeśli nie masz jeszcze zainstalowanego OpenCV, otwórz Terminal i uruchom:
pip install opencv-python
teraz Sklonuj repozytorium samouczka, uruchamiając:
git clone https://github.com/chuanenlin/optical-flow.git
następnie otwórz repozytorium sparse-starter.py za pomocą edytora tekstu. Będziemy pisać cały kod w tym Pliku Pythona.
Konfigurowanie OpenCV do odczytu wideo i konfigurowanie parametrów
Shi-Tomasi Corner Detector – wybieranie pikseli do śledzenia
w celu realizacji rzadkiego przepływu optycznego śledzimy tylko ruch zestawu funkcji pikseli. Funkcje w obrazach są punktami zainteresowania, które prezentują bogate informacje o treści obrazu. Na przykład takimi cechami mogą być punkty obrazu, które są niezmienne dla zmian translacji, skali, obrotu i intensywności, takich jak narożniki.
Detektor narożny Shi-Tomasi jest bardzo podobny do popularnego detektora narożnego Harrisa, który może być zaimplementowany za pomocą następujących trzech procedur:
- określanie okien (małych łat obrazu) z dużymi gradientami (zmiany intensywności obrazu) po przetłumaczeniu w kierunkach \(x\) i \(y\).
- dla każdego okna Oblicz wynik \(R\).
- w zależności od wartości \(R\), każde okno jest klasyfikowane jako płaskie, krawędź lub narożnik.
Jeśli chcesz dowiedzieć się więcej na temat matematycznego wyjaśnienia krok po kroku detektora narożnego Harrisa, przejrzyj te slajdy.
Shi i Tomasi zrobili później małą, ale skuteczną modyfikację detektora narożnego Harrisa w swoim papierze Good Features to Track.
zmiana polega na równaniu, w którym obliczany jest wynik \(R\). W detektorze narożnym Harrisa funkcja punktowania jest dana przez:
$$
\begin{array}{c}{R=\operatorname{det} m-k(\operatorname{trace} m)^{2}}\newline \
{\operatorname{det} M=\lambda_{1} \lambda_{2}}\newline \
{\operatorname{trace} M=\lambda_{1}+\lambda_{2}}\end{array}
$$
zamiast tego shi-Tomasi zaproponował funkcję punktowania jako:
$$
r=\min \Left(\lambda_{1}, \lambda_{2}\Right)
$$
co zasadniczo oznacza, że jeśli \(R\) jest większa niż próg, jest klasyfikowana jako róg. Poniższe zestawienie porównuje funkcje punktowe Harrisa (po lewej) i Shi-Tomasiego (po prawej) w przestrzeni \(λ1-λ2\).
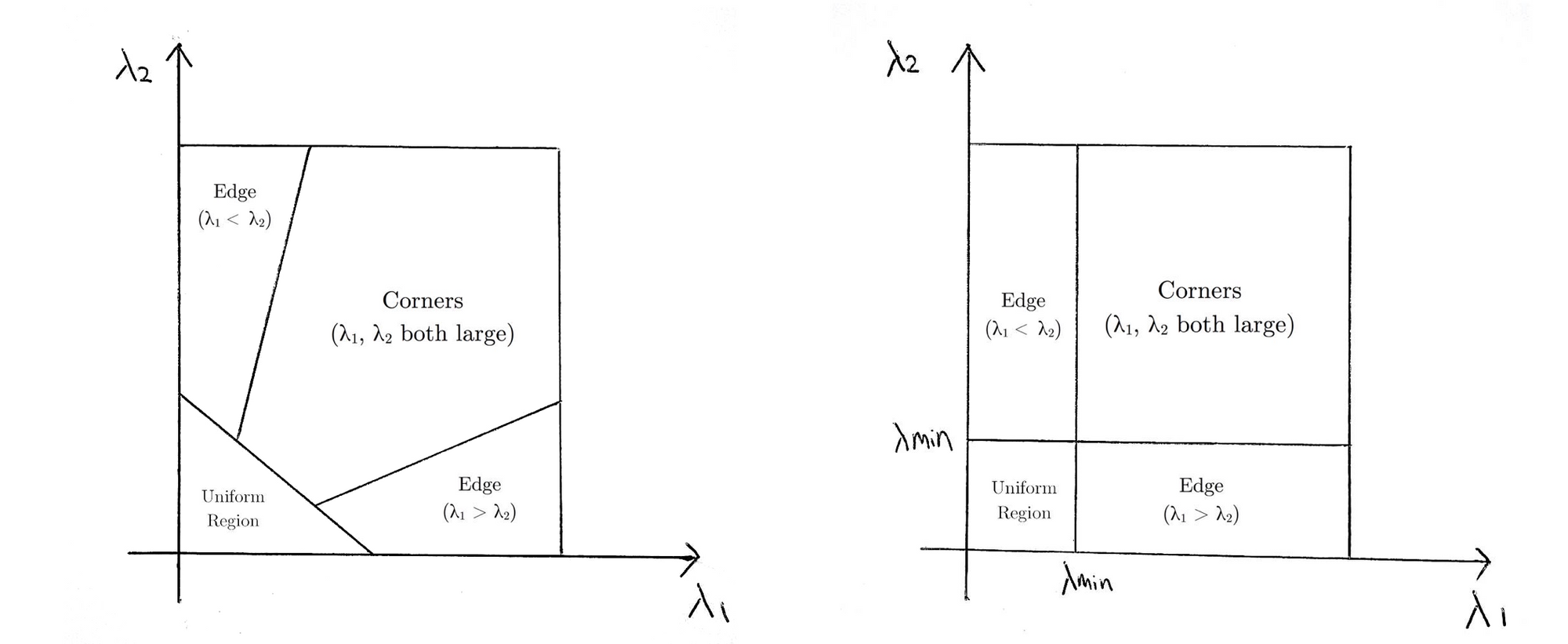
dla Shi-Tomasi, tylko wtedy, gdy \(λ1\) i \(λ2\) są powyżej minimalnego progu \(λmin\), okno jest klasyfikowane jako narożnik.
dokumentacja implementacji Shi-Tomasi przez OpenCV poprzez goodFeaturesToTrack() znajduje się tutaj.
śledzenie konkretnych obiektów
mogą istnieć scenariusze, w których chcesz śledzić tylko określony obiekt zainteresowania (powiedzmy śledzenie określonej osoby) lub jedną kategorię obiektów (jak wszystkie pojazdy 2-kołowe w ruchu drogowym). Możesz łatwo zmodyfikować kod, aby śledzić piksele pożądanych obiektów, zmieniając zmiennąprev.
Możesz również połączyć wykrywanie obiektów z tą metodą, aby oszacować przepływ pikseli w wykrytych obwiedniach. W ten sposób możesz śledzić wszystkie obiekty określonego typu/kategorii w filmie.
Lucas-Kanade: Sparse Optical Flow
Lucas i Kanade zaproponowali skuteczną technikę szacowania ruchu interesujących elementów poprzez porównanie dwóch kolejnych klatek w swojej pracy iteracyjnej Techniki Rejestracji obrazu z aplikacją do widzenia stereoskopowego. Metoda Lucasa-Kanade działa w oparciu o następujące założenia:
- dwie kolejne klatki są oddzielone małym przyrostem czasowym (\(dt\)) tak, że obiekty nie są znacznie przesunięte (innymi słowy, metoda działa najlepiej z wolno poruszającymi się obiektami).
- ramka przedstawia „naturalną” scenę z teksturowanymi obiektami eksponującymi odcienie szarości, które zmieniają się płynnie.
Po pierwsze, zgodnie z tymi założeniami, możemy wziąć małe okno 3×3 (sąsiedztwo) wokół cech wykrywanych przez Shi-Tomasiego i założyć, że wszystkie dziewięć punktów ma ten sam ruch.
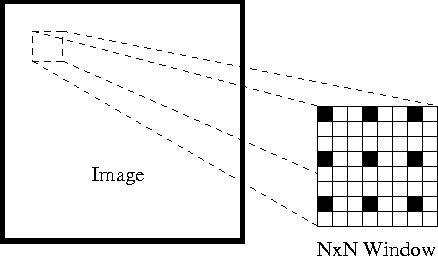
może to być reprezentowane jako
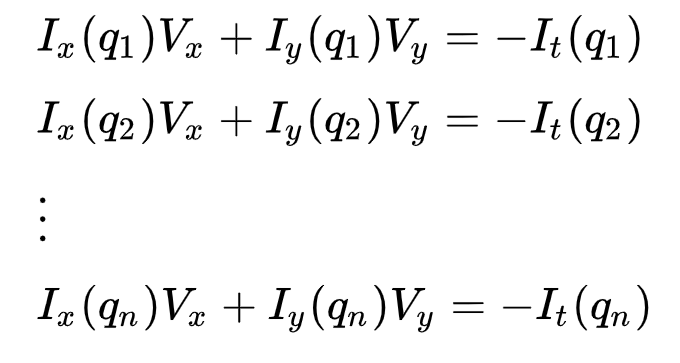
gdzie \(q_1, q_2, …, q_n\) oznacza piksele wewnątrz okna (np. \(N\) = 9 dla okna 3×3) i \(i_x(q_i)\), \(i_y(q_i)\) i \(i_t(q_i)\) oznaczają częściowe pochodne obrazu \(i\) względem pozycji \((X, Y)\) i Time \(T\), dla Pixela \(q_i\) w bieżącym czasie.
To jest po prostu równanie przepływu optycznego (które opisaliśmy wcześniej) dla każdego z n pikseli.
zbiór równań może być przedstawiony w następującej postaci macierzy, gdzie \(av = b\):
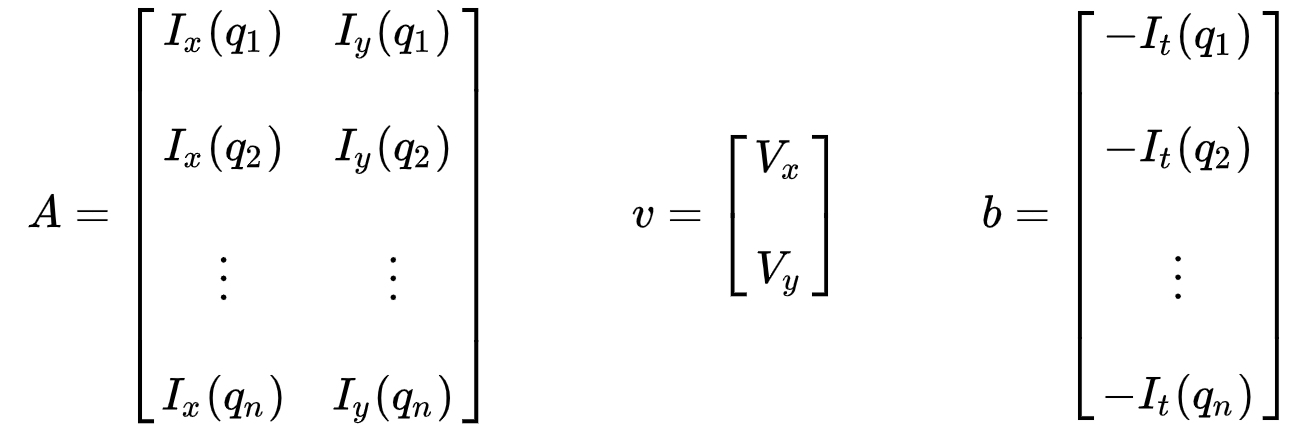
zwróć uwagę, że wcześniej (patrz „co to jest przepływ optyczny?”sekcja), stanęliśmy przed problemem konieczności rozwiązania dla dwóch nieznanych zmiennych za pomocą jednego równania. Teraz musimy rozwiązać dwie niewiadome (\(v_x\) i \(V_y\)) z dziewięcioma równaniami, które są przesadnie określone.
Po drugie, aby rozwiązać problem nadmiernie określony, stosujemy najmniejsze kwadraty, aby uzyskać następujący problem dwu-równań-dwóch-nieznanych:
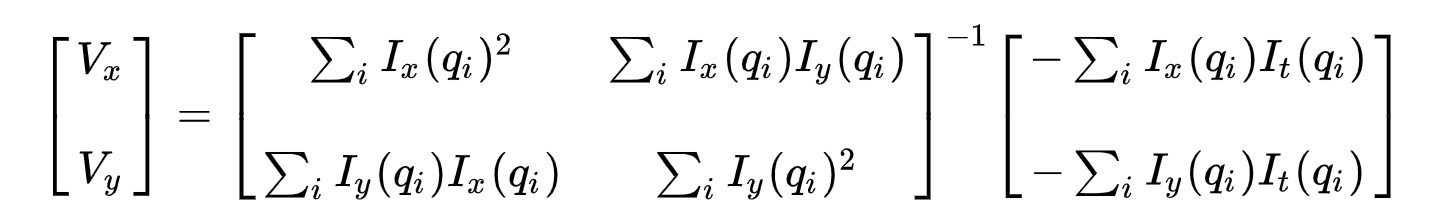
gdzie \(VX = u = DX/DT\) oznacza ruch \(X\) w czasie i \(vy = V = dy / DT\) oznacza ruch y w czasie. Rozwiązanie dwóch zmiennych uzupełnia problem przepływu optycznego.

w skrócie, identyfikujemy kilka interesujących funkcji do śledzenia i iteracyjnie obliczamy optyczne wektory przepływu tych punktów. Jednak przyjęcie metody Lucasa-Kanade działa tylko dla małych ruchów (z naszego początkowego założenia) i zawodzi, gdy istnieje duży ruch. Dlatego implementacja OpenCV metody Lucasa-Kanade przyjmuje piramidy.
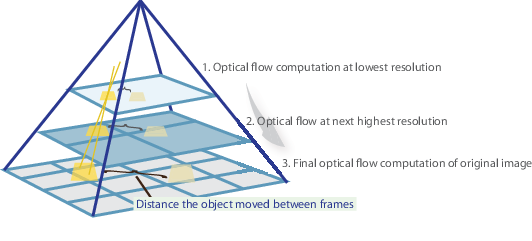
w widoku wysokiego poziomu małe ruchy są pomijane, gdy idziemy w górę piramidy, a duże ruchy są redukowane do małych ruchów-obliczamy przepływ optyczny wraz ze skalą. Obszerne matematyczne Wyjaśnienie implementacji OpenCV można znaleźć w notatkach Bougueta, a dokumentację implementacji OpenCV metody Lucas-Kanade poprzez calcOpticalFlowPyrLK() można znaleźć tutaj.
i tyle! Otwórz Terminal i uruchom
python sparse-starter.py
, aby przetestować implementację rzadkiego przepływu optycznego. 👏
w przypadku pominięcia jakiegokolwiek kodu, Pełny kod można znaleźć w sparse-solution.py.
implementując gęsty przepływ optyczny
wcześniej obliczyliśmy przepływ optyczny dla rzadkiego zestawu funkcji pikseli. Gęsty przepływ optyczny próbuje obliczyć wektor przepływu optycznego dla każdego piksela każdej klatki. Podczas gdy takie obliczenia mogą być wolniejsze, daje bardziej dokładny wynik i gęstszy wynik odpowiedni do zastosowań takich jak uczenie się struktury z ruchu i segmentacji wideo. Istnieją różne implementacje gęstego przepływu optycznego. Będziemy używać metody Farneback, jednej z najpopularniejszych implementacji, z wykorzystaniem OpenCV, biblioteki open source algorytmów wizji komputerowej, do implementacji.
Konfigurowanie środowiska
Jeśli jeszcze tego nie zrobiłeś, wykonaj krok 1 implementacji rzadkiego przepływu optycznego, aby skonfigurować środowisko.
następny, otwórz dense-starter.py za pomocą edytora tekstu. Będziemy pisać cały kod w tym Pliku Pythona.
Konfigurowanie OpenCV do odczytu wideo
przepływ optyczny Farneback
Gunnar Farneback zaproponował skuteczną technikę szacowania ruchu interesujących funkcji poprzez porównanie dwóch kolejnych klatek w swojej pracy oszacowanie ruchu Dwuramkowego oparte na ekspansji wielomianowej.
Po pierwsze, metoda przybliża okna (zobacz sekcję Lucas Kanade o implementacji sparse optical flow po więcej szczegółów) klatek obrazu przez wielomiany kwadratowe poprzez wielomianową transformatę ekspansji. Po drugie, obserwując, jak wielomian przekształca się pod wpływem translacji (ruchu), definiuje się metodę szacowania pól przemieszczeń ze współczynników rozszerzalności wielomianów. Po serii udoskonaleń obliczany jest gęsty przepływ optyczny. Papier Farneback jest dość zwięzły i prosty do naśladowania, więc gorąco polecam przejrzenie papieru, jeśli chcesz lepszego zrozumienia jego matematycznej derywacji.

dla implementacji OpenCV oblicza wielkość i kierunek przepływu optycznego z 2-kanałowej tablicy wektorów przepływu \((dx/dt, dy/dt)\), problem przepływu optycznego. Następnie wizualizuje kąt (kierunek) przepływu według barwy i odległość (wielkość) przepływu według wartości reprezentacji kolorów HSV. Siła HSV jest zawsze ustawiona na maksymalnie 255 dla optymalnej widoczności. Dokumentacja implementacji metody Farneback przez OpenCV poprzez calcOpticalFlowFarneback() znajduje się tutaj.
i tyle! Otwórz Terminal i uruchom
python dense-starter.py
, aby przetestować implementację gęstego przepływu optycznego. 👏
w przypadku pominięcia jakiegokolwiek kodu, Pełny kod można znaleźć w dense-solution.py.
przepływ optyczny przy użyciu głębokiego uczenia
chociaż problem przepływu optycznego był historycznie problemem optymalizacyjnym, Ostatnie podejścia przy użyciu głębokiego uczenia wykazały imponujące wyniki. Zasadniczo takie podejścia przyjmują dwie klatki wideo jako wejście do wyjścia przepływu optycznego (obraz kodowany kolorami), który może być wyrażony jako:
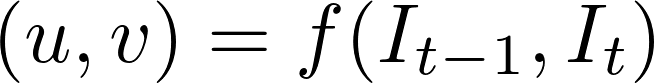

gdzie \(u\) jest ruchem w kierunku \(x\), \(v\) jest ruchem w kierunku \(y\), A \(f\) jest siecią neuronową, która przyjmuje dwie kolejne klatki \(i_{t-1}\) (frame at time = \(t-1)\) i \(i_t\) (frame at time = \(t)\) jako wejście.
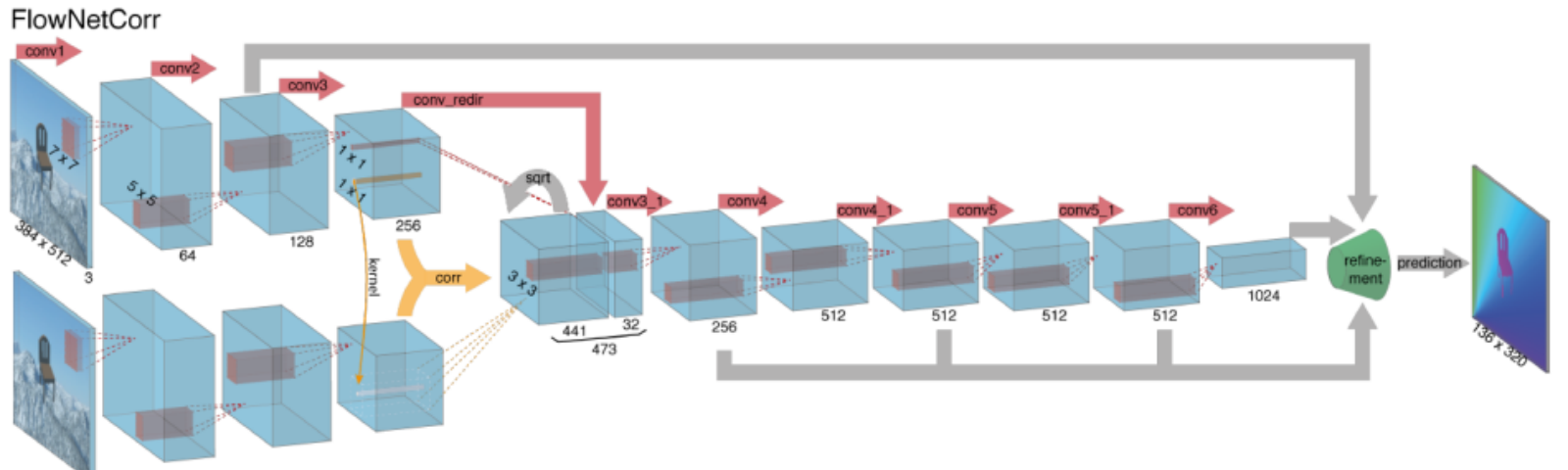
Obliczanie przepływu optycznego za pomocą głębokich sieci neuronowych wymaga dużych ilości danych treningowych, które są szczególnie trudne do uzyskania. Wynika to z faktu, że etykietowanie materiału wideo pod kątem przepływu optycznego wymaga dokładnego określenia dokładnego ruchu każdego punktu obrazu z dokładnością do subpikseli. Aby rozwiązać problem etykietowania danych szkoleniowych, naukowcy wykorzystali grafikę komputerową do symulacji masywnych realistycznych światów. Ponieważ światy są generowane przez instrukcje, ruch każdego punktu obrazu w sekwencji wideo jest znany. Niektóre przykłady takich obejmują MPI-Sintel, film open-source CGI z etykietowaniem przepływu optycznego renderowanym dla różnych sekwencji, i latające krzesła, zbiór danych wielu krzeseł latających w losowych tłach również z etykietowaniem przepływu optycznego.


Rozwiązywanie problemów z przepływem optycznym za pomocą głębokiego uczenia jest obecnie niezwykle gorącym tematem, z wariantami FlowNet, SpyNet, PWC-Net i innymi, które przewyższają się nawzajem w różnych benchmarkach.
zastosowanie przepływu optycznego: segmentacja semantyczna
pole przepływu optycznego jest ogromną kopalnią informacji dla obserwowanej sceny. Ponieważ techniki dokładnego określania przepływu optycznego poprawiają się, interesujące jest zobaczenie zastosowań przepływu optycznego w połączeniu z kilkoma innymi podstawowymi zadaniami wizji komputerowych. Na przykład zadaniem segmentacji semantycznej jest podzielenie obrazu na serie regionów odpowiadających unikalnym klasom obiektów, jednak ściśle umieszczone obiekty o identycznych teksturach są często trudne dla technik segmentacji pojedynczej klatki. Jeśli jednak obiekty są umieszczone oddzielnie, wyraźne ruchy obiektów mogą być bardzo pomocne, gdy nieciągłość w gęstym polu przepływu optycznego odpowiada granicami między obiektami.
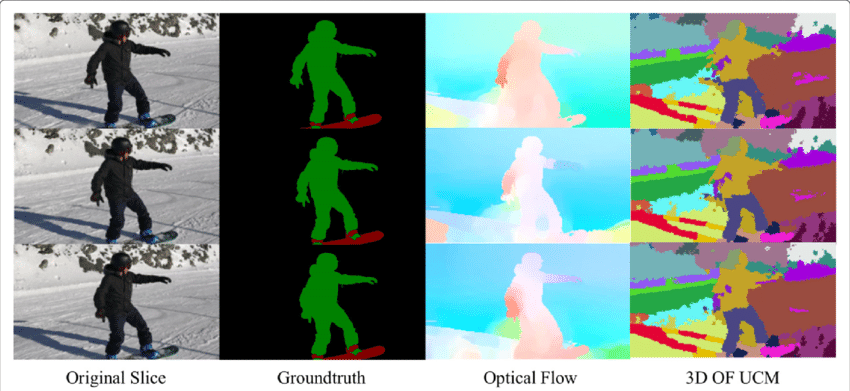
zastosowanie przepływu optycznego: wykrywanie obiektów& śledzenie
kolejnym obiecującym zastosowaniem przepływu optycznego może być wykrywanie i śledzenie obiektów lub, w formie wysokiego poziomu, budowanie systemów śledzenia pojazdów i analizy ruchu w czasie rzeczywistym. Ponieważ niewielki przepływ optyczny wykorzystuje śledzenie punktów zainteresowania, takie systemy czasu rzeczywistego mogą być wykonywane za pomocą opartych na cechach technik przepływu optycznego z kamery stacjonarnej lub kamer przymocowanych do pojazdów.


wniosek
zasadniczo wektory przepływu optycznego działają jako wejście do niezliczonej liczby zadań wyższego poziomu wymagających zrozumienia sekwencji wideo, podczas gdy zadania te mogą dalej działać jako elementy składowe jeszcze bardziej złożonych systemów, takich jak analiza wyrazu twarzy, nawigacja autonomicznego pojazdu i wiele innych. Nowe zastosowania przepływu optycznego, które jeszcze nie zostały odkryte, są ograniczone jedynie pomysłowością jego projektantów.
leniwy w kodowaniu, nie chcesz wydawać na GPU? Udaj się do Nanonets i twórz modele komputerowej wizji za darmo!