Zrozumienie Deep Residual Networks

Deep residual networks (ResNet) podbiło świat głębokiego uczenia się, gdy Microsoft Research opublikował Deep Residual Learning do rozpoznawania obrazów. Sieci te doprowadziły do zdobycia pierwszego miejsca we wszystkich pięciu głównych konkursach ImageNet i COCO 2015, które obejmowały klasyfikację obrazów, wykrywanie obiektów i segmentację semantyczną. Solidność ResNets została od tego czasu udowodniona przez różne zadania rozpoznawania wizualnego i zadania niewizualne obejmujące mowę i język. Oprócz innych modeli deep learning wykorzystałem również ResNet w badaniach nad rozprawą doktorską.

ten post podsumuje trzy poniższe artykuły, które są napisane lub napisane wspólnie przez wynalazcę ResNet Kaiming He, ponieważ wierzę, że oryginalne artykuły dają najbardziej intuicyjne i szczegółowe wyjaśnienie modelu/sieci. Mam nadzieję, że ten post pomoże Ci lepiej zrozumieć istotę pozostałych sieci.

• głębokie uczenie szczątkowe do rozpoznawania obrazów
• mapowanie tożsamości w głębokich sieciach szczątkowych
• zagregowana transformacja szczątkowa dla głębokich sieci neuronowych

intuicja w sieci głębokich szczątkowych (stackoverflow ref)

blok resztkowy jest wyświetlany w następujący sposób:

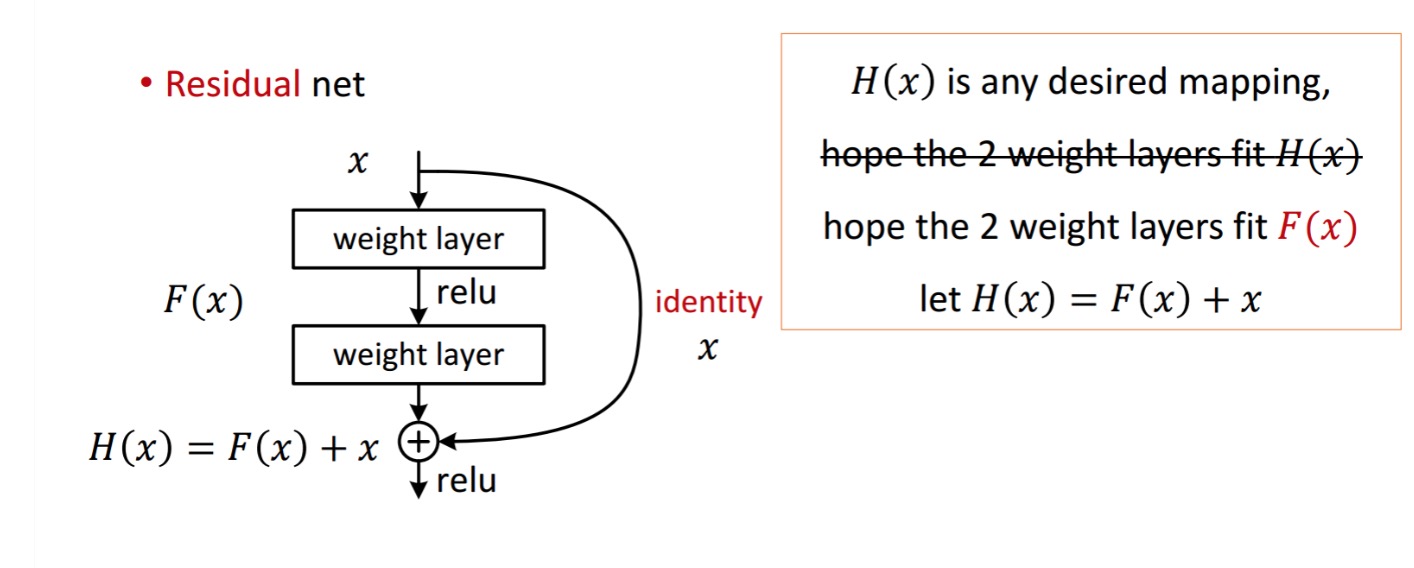
tak więc pokazana jednostka resztkowa uzyskuje się przez przetwarzanie za pomocą dwóch warstw wagowych. Następnie dodaje się do uzyskania . Załóżmy, że jest to twój idealny przewidywany wynik, który pasuje do Twojej prawdy. Ponieważ uzyskanie pożądanego zależy od uzyskania idealnego . Oznacza to , że dwie warstwy wagowe w jednostce resztkowej powinny być w stanie wyprodukować pożądaną, a następnie zagwarantować ideał.

otrzymuje się z następujących

otrzymuje się z następujących

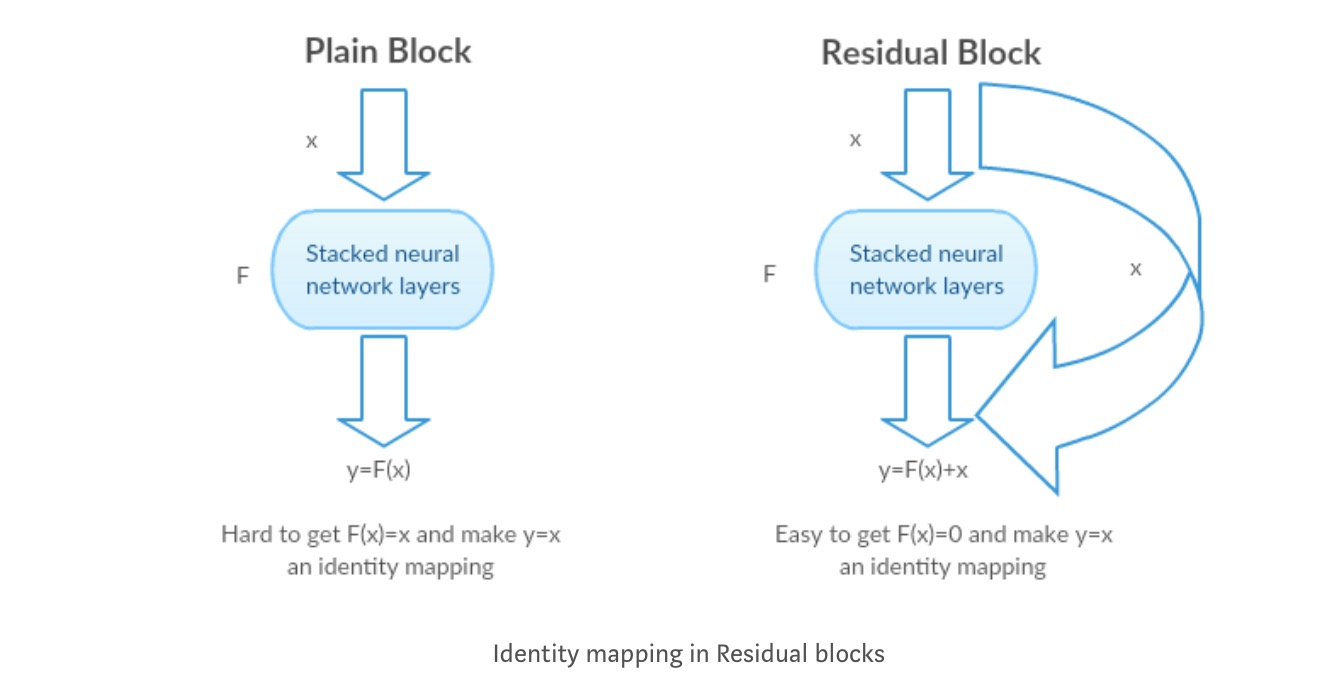
autorzy stawiają hipotezę, że mapowanie resztkowe (tj. ) może być łatwiejsze do optymalizacji niż . Aby zilustrować za pomocą prostego przykładu, załóżmy, że ideał . Następnie dla bezpośredniego mapowania trudno byłoby nauczyć się mapowania tożsamości, ponieważ istnieje stos nieliniowych warstw w następujący sposób.

więc przybliżenie odwzorowania tożsamości ze wszystkimi tymi wagami i Relusem w środku byłoby trudne.

teraz, jeśli zdefiniujemy pożądane mapowanie, to po prostu potrzebujemy uzyskać w następujący sposób.

osiągnięcie powyższego jest łatwe. Po prostu ustaw dowolną wagę na zero, a otrzymasz zerowe wyjście. Dodaj z powrotem, a otrzymasz pożądane mapowanie.

głębokie uczenie szczątkowe do rozpoznawania obrazów

Problem

gdy głębsze sieci zaczynają się zbliżać, problem degradacji został ujawniony: wraz ze wzrostem głębokości sieci dokładność zostaje nasycona, a następnie szybko się degraduje.

widząc degradację w akcji:

weźmy płytką Sieć i jej głębszy odpowiednik, dodając do niej kolejne warstwy.

najgorszy scenariusz: wczesne warstwy modelu mogą być zastąpione płytką siecią, a pozostałe warstwy mogą po prostu działać jako funkcja tożsamościowa (wejście równe wyjściu).

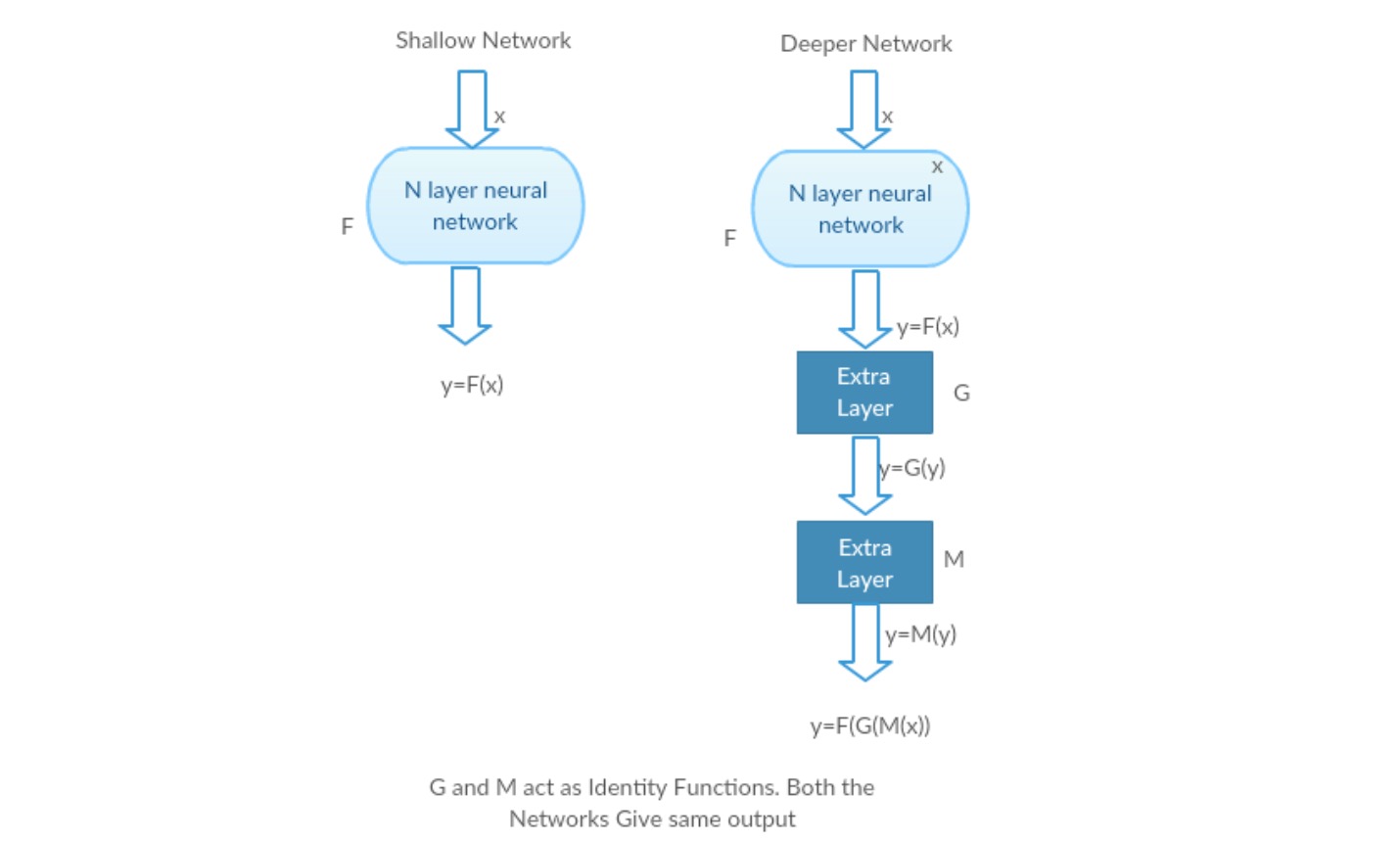
Scenariusz nagradzania: w głębszej sieci dodatkowe warstwy lepiej przybliżają mapowanie niż płytsza część licznika i zmniejszają błąd o znaczny margines.

eksperyment: W najgorszym przypadku zarówno płytka sieć, jak i jej głębszy wariant powinny dawać taką samą dokładność. W przypadku scenariusza satysfakcjonującego, głębszy model powinien dawać lepszą dokładność niż płytsza część licznika. Ale eksperymenty z naszymi obecnymi rozwiązaniami pokazują, że głębsze modele nie działają dobrze. Tak więc używanie głębszych sieci pogarsza wydajność modelu. Artykuły te próbują rozwiązać ten problem za pomocą Deep Residual learning framework.

Jak rozwiązać?

zamiast uczyć się bezpośredniego mapowania za pomocą funkcji (kilka ułożonych warstw nieliniowych). Zdefiniujmy funkcję rezydualną za pomocą , którą można przekształcić w, gdzie i reprezentuje ułożone warstwy nieliniowe i funkcję tożsamościową(wejście=wyjście) odpowiednio.

hipoteza autora jest taka, że łatwo jest zoptymalizować pozostałą funkcję mapowania niż zoptymalizować oryginalne, nieferencjowane mapowanie .

intuicja za resztkowymi blokami:

weźmy mapowanie tożsamości jako przykład (np. ). Jeśli mapowanie tożsamości jest optymalne, możemy łatwo przesunąć pozostałości do zera () niż dopasować mapowanie tożsamości za pomocą stosu nieliniowych warstw. W prostym języku bardzo łatwo jest wymyślić rozwiązanie takie jak zamiast używać stosu nieliniowych warstw cnn jako funkcji (pomyśl o tym). Tak więc, ta funkcja jest tym, co autorzy nazwali funkcją resztkową.

autorzy wykonali kilka testów, aby sprawdzić swoją hipotezę. Spójrzmy teraz na każdą z nich.

przypadki testowe:

weź zwykłą sieć (VGG kind 18 layer network) (Network-1) i głębszy jej wariant (34-layer, Network-2) i dodaj warstwy resztkowe do sieci-2 (34 warstwy z resztkowymi połączeniami, Network-3).

projektowanie sieci:

1. najczęściej Używaj filtrów 3*3.
2. próbkowanie w dół warstwami CNN z krokiem 2.
3. globalna średnia warstwa poolingu i 1000-drożna w pełni połączona warstwa z Softmax w końcu.

istnieją dwa rodzaje połączeń resztkowych:

I. skróty identyfikacyjne () mogą być bezpośrednio użyte, gdy input () I output () mają te same wymiary.

II. po zmianie wymiarów, a) Skrót nadal wykonuje mapowanie tożsamości, z dodatkowymi wpisami zerowymi wypełnionymi zwiększonym wymiarem. B) Skrót projekcji jest używany do dopasowania wymiaru (wykonywanego przez 1 * 1 conv) za pomocą następującego wzoru

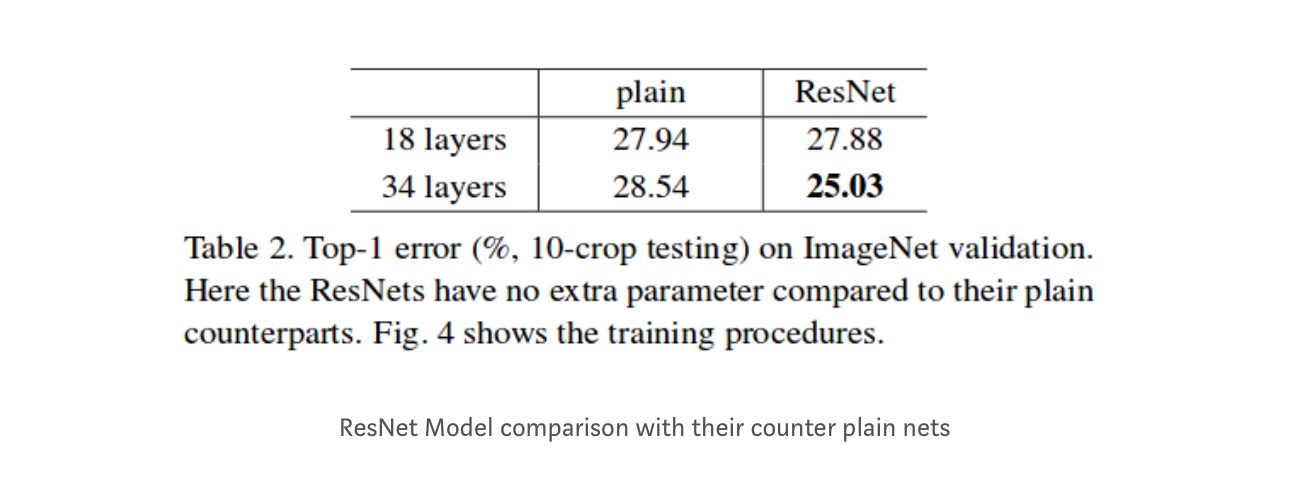
wyniki

mimo że sieć 18 warstw jest tylko podprzestrzenią w sieci 34 warstwowej, nadal działa lepiej. ResNet przewyższa znaczącym marginesem w przypadku, gdy sieć jest głębsza

głębsze badania

ponadto badane są kolejne sieci:

każdy blok Resnetu jest głęboki na dwie warstwy (używany do w małych sieciach, takich jak ResNet 18, 34) lub 3 warstwy Deep( ResNet 50, 101, 152).

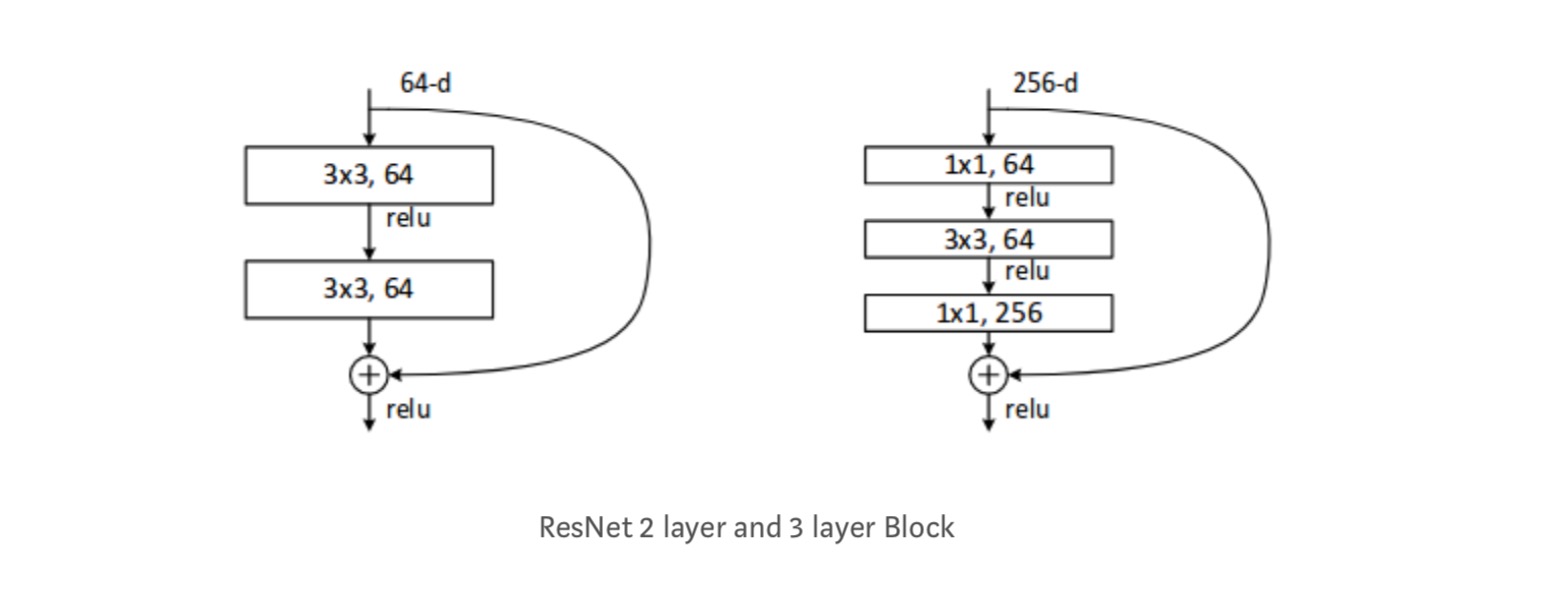
obserwacje

1. sieć ResNet zbiega się szybciej niż zwykła jej część licznikowa.
2. tożsamość vs projekcja shorcuts. Bardzo małe przyrostowe zyski za pomocą skrótów projekcyjnych (równanie-2) we wszystkich warstwach. Tak więc wszystkie bloki ResNet używają tylko skrótów tożsamościowych, a skróty projekcyjne używane tylko wtedy, gdy zmieniają się wymiary.
3. ResNet-34 uzyskał błąd walidacji top-5 o 5,71% lepszy niż BN-inception i VGG. ResNet-152 osiąga błąd walidacji top-5 na poziomie 4,49%. Zespół 6 modeli o różnych głębokościach osiąga błąd walidacji top-5 na poziomie 3,57%. Zdobycie 1. miejsca w ILSVRC-2015

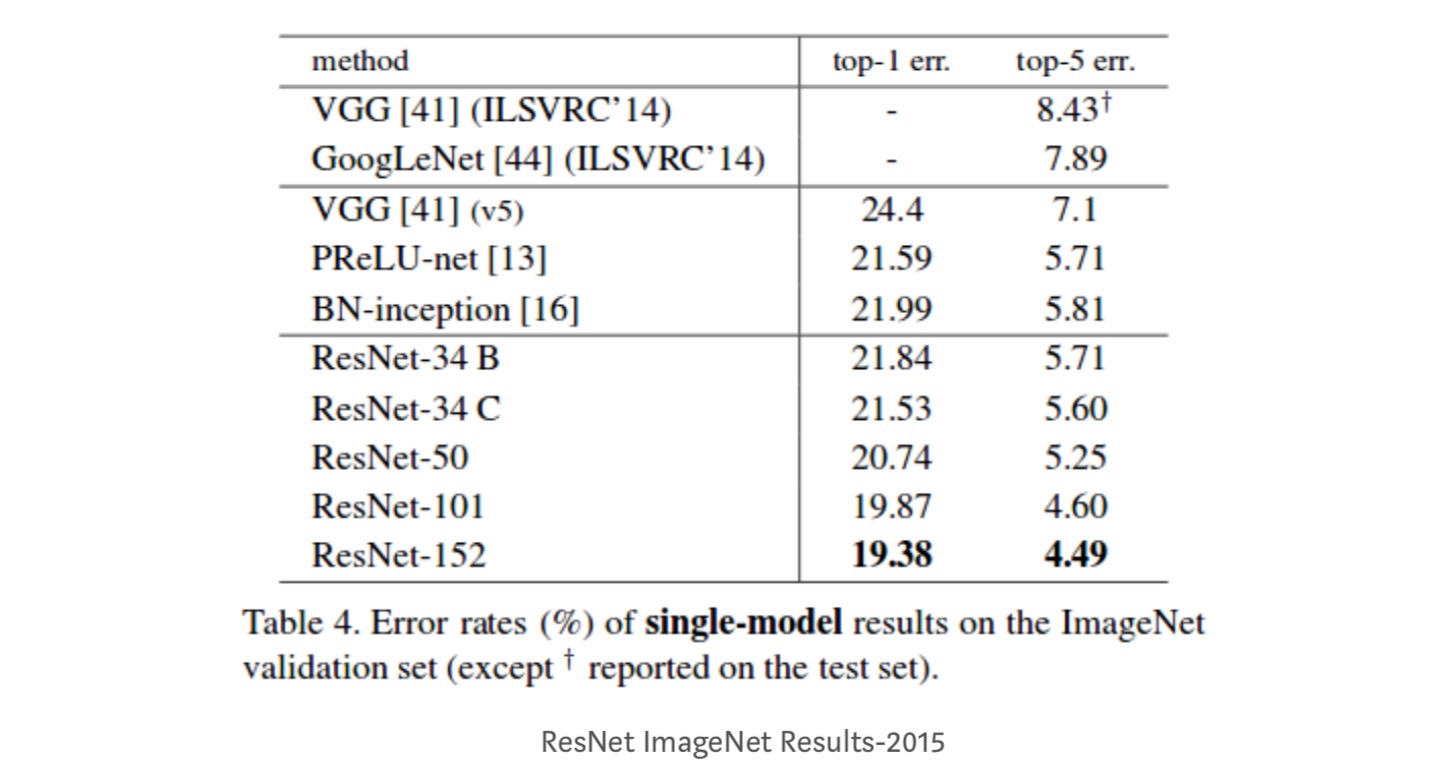
mapowanie tożsamości w głębokich sieciach szczątkowych

w artykule przedstawiono teoretyczne zrozumienie, dlaczego problem znikającego gradientu nie występuje w sieciach szczątkowych oraz rolę pomijania połączeń (pomijanie połączeń oznacza wejście lub ) poprzez zastąpienie mapowania tożsamości (x) różnymi funkcjami.

wprowadzenie

Głębokie sieci szczątkowe składają się z wielu ułożonych „jednostek resztkowych”. Każda jednostka może być wyrażona w postaci ogólnej:

gdzie i są wejściami i wyjściami jednostki i są funkcją rezydualną. W ostatnim artykule jest odwzorowaniem tożsamości i jest funkcją ReLU.

główną ideą Resnetów jest poznanie addytywnej funkcji resztkowej w odniesieniu do , z kluczowym wyborem użycia mapowania tożsamości . Jest to realizowane przez dołączenie połączenia pominięcia tożsamości („Skrót”).

w tym artykule analizujemy Głębokie sieci szczątkowe, koncentrując się na tworzeniu „bezpośredniej” ścieżki propagacji informacji — nie tylko w obrębie jednostki resztkowej, ale przez całą sieć. Nasze wyprowadzenia ujawniają, że jeśli oba i są odwzorowaniami tożsamościowymi, sygnał może być bezpośrednio propagowany z jednej jednostki do innych jednostek, zarówno w przejściu do przodu, jak i do tyłu. Nasze eksperymenty empirycznie pokazują, że szkolenie w ogóle staje się łatwiejsze, gdy architektura jest bliżej powyższych dwóch warunków.

aby zrozumieć rolę połączeń pomiń, analizujemy i porównujemy różne rodzaje. Okazuje się, że mapowanie tożsamości wybrane w ostatnim artykule zapewnia najszybszą redukcję błędów i najniższą stratę treningową spośród wszystkich zbadanych przez nas wariantów, podczas gdy pominięcie połączeń skalowania , bramkowania i splotu 1×1 prowadzi do większych strat treningowych i błędów. Eksperymenty te sugerują, że utrzymanie” czystej ” ścieżki informacyjnej jest pomocne dla ułatwienia optymalizacji.

aby skonstruować mapowanie tożsamości , postrzegamy funkcje aktywacyjne (ReLU i BN) jako „pre-aktywację” warstw wagowych, w przeciwieństwie do konwencjonalnej mądrości „po aktywacji”. Ten punkt widzenia prowadzi do nowego projektu jednostki resztkowej, pokazanego na poniższym rysunku. W oparciu o tę jednostkę prezentujemy konkurencyjne wyniki na CIFAR – 10/100 z 1001-warstwowym Resnetem, który jest znacznie łatwiejszy w szkoleniu i generalizuje lepiej niż oryginalny ResNet. Ponadto raportujemy lepsze wyniki na ImageNet za pomocą 200-warstwowego Resnetu, dla którego odpowiednik ostatniego artykułu zaczyna się nadpisywać. Wyniki te sugerują, że istnieje wiele możliwości wykorzystania wymiaru głębokości sieci, kluczowego dla sukcesu nowoczesnego uczenia głębokiego.

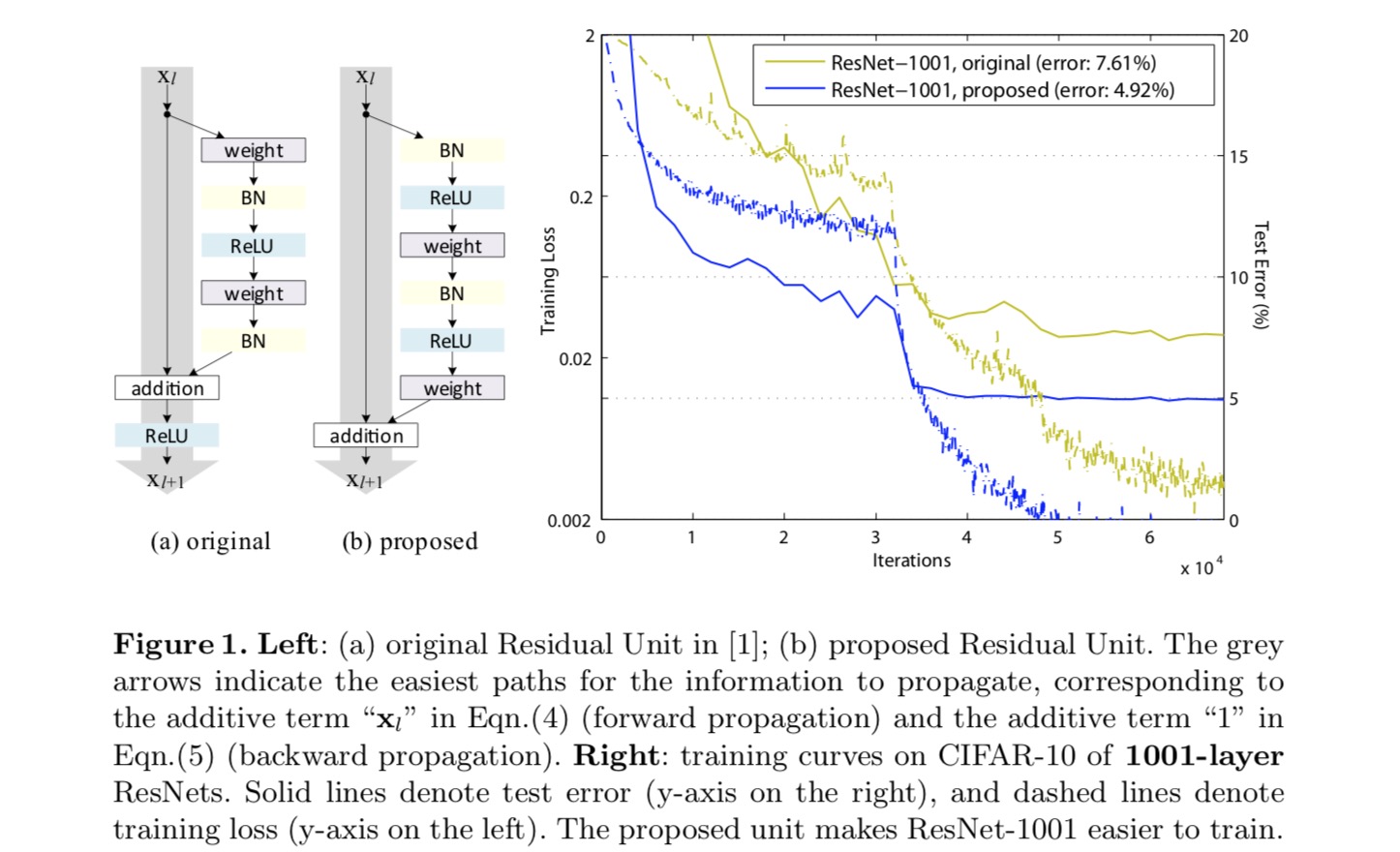
Analiza głębokich sieci resztkowych

Resnety opracowane w ostatnim artykule są modułowymi architekturami stosowymi bloków konstrukcyjnych o tym samym kształcie połączenia. W tym artykule nazywamy te bloki „jednostkami resztkowymi”. Oryginalna Jednostka resztkowa w ostatnim artykule wykonuje następujące obliczenia:

tutaj znajduje się funkcja wprowadzania do-tej jednostki resztkowej. jest zestaw wag ( i uprzedzeń) związanych z-th jednostki resztkowej, i jest liczba warstw w jednostce resztkowej (jest 2 lub 3 w ostatnim papierze). oznacza funkcję resztkową, np.g., stos dwóch warstw splotu 3×3 w ostatnim papierze. Funkcja jest operacją po dodaniu elementów, a w ostatnim artykule jest ReLU. Funkcja jest ustawiona jako odwzorowanie tożsamości: .

Jeśli jest również mapowaniem tożsamości: , możemy uzyskać:

rekurencyjnie będziemy mieli:

dla każdej głębszej jednostki i każdej płytszej jednostki . Równanie to wykazuje pewne niceproperty. (1) cecha każdej głębszej jednostki może być reprezentowana jako cecha każdej płytszej jednostki plus Funkcja resztkowa w postaci , wskazując, że model jest w sposób szczątkowy między dowolnymi jednostkami i . (2) cechą każdej jednostki głębokiej jest sumowanie wyjść wszystkich poprzedzających funkcji resztkowych (plus). Jest to przeciwieństwo „zwykłej sieci”, w której cechą jest seria iloczynów macierzowo-wektorowych, np. (ignorując BN i ReLU).

powyższe równanie prowadzi również do ładnych właściwości propagacji wstecznej. Oznaczając funkcję stratną jako, z reguły łańcuchowej odwrotności mamy:

powyższe równanie wskazuje, że gradient można rozkładać na dwa addytywne wyrazy: określenie to propaguje informacje bezpośrednio, Nie dotyczące żadnych warstw wagowych, a inne określenie tego propaguje poprzez warstwy wagowe. Addytywny termin zapewnia, że informacje są bezpośrednio propagowane z powrotem do dowolnej płytszej jednostki l. powyższe równanie sugeruje również, że jest mało prawdopodobne, aby gradient został anulowany dla mini-partii, ponieważ ogólnie termin ten nie zawsze może być -1 dla wszystkich próbek w mini-partii. Oznacza to, że gradient warstwy nie zanika nawet wtedy, gdy wagi są arbitralnie małe.

powyższe dwa równania sugerują, że sygnał może być bezpośrednio propagowany z dowolnej jednostki do innej, zarówno do przodu, jak i do tyłu. Podstawą pierwszych powyższych dwóch równań są dwa odwzorowania tożsamości: (1) połączenie pominięcia tożsamości i (2) warunek , który jest odwzorowaniem tożsamości.

Znaczenie tożsamości pomiń połączenia

rozważmy prostą modyfikację, , aby złamać Skrót tożsamości:

Gdzie jest Skalar modulujący (dla uproszczenia nadal Zakładamy tożsamość). Rekurencyjnie stosując to sformułowanie otrzymujemy równanie podobne do powyższego:

gdzie notacja pochłania Skalary do funkcji resztowych. Podobnie mamy odwrotność następującej postaci:

w przeciwieństwie do poprzedniego równania, w tym równaniu pierwszy addytywny termin jest modulowany przez czynnik . Dla bardzo głębokiej sieci (jest duża), jeśli dla wszystkich , czynnik ten może być wykładniczo duży; jeśli dla wszystkich , czynnik ten może być wykładniczo mały i zniknąć, co blokuje sygnał zwrotny ze skrótu i zmusza go do przepływu przez warstwy wagowe. Powoduje to trudności optymalizacyjne, jak pokazujemy w eksperymentach.

w powyższej analizie oryginalne połączenie pominięcia tożsamości zostaje zastąpione prostym skalowaniem . Jeśli połączenie skip reprezentuje bardziej skomplikowane transformaty (takie jak gating i 1×1 sploty), w powyższym równaniu pierwszy wyraz staje się gdzie jest pochodną . Produkt ten może również utrudniać rozprzestrzenianie się informacji i utrudniać procedurę treningową, o której świadczyły następujące doświadczenia.

eksperymenty na połączeniach Skip

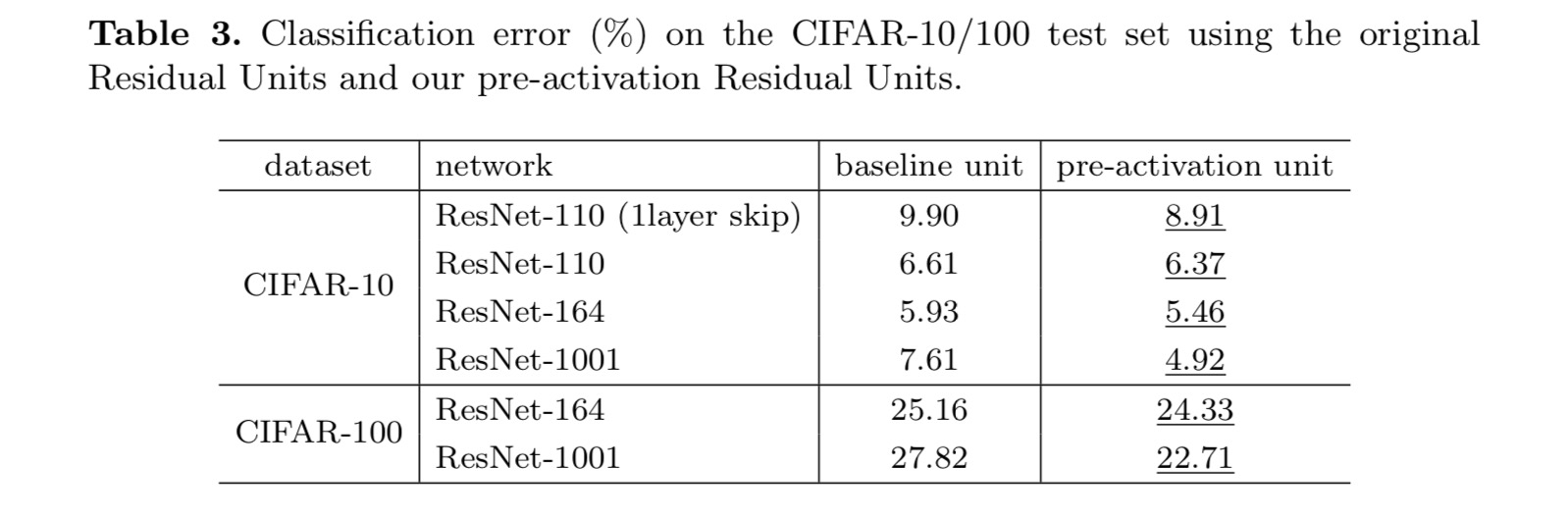
eksperymentujemy z 110-warstwowym Resnetem na CIFAR-10. Ten niezwykle głęboki ResNet-110 ma 54 dwuwarstwowe jednostki resztkowe (składające się z 3×3 warstw splotu) i jest trudny do optymalizacji. Eksperymentuje się z różnymi rodzajami połączeń pominiętych. Zobacz poniższy rysunek:

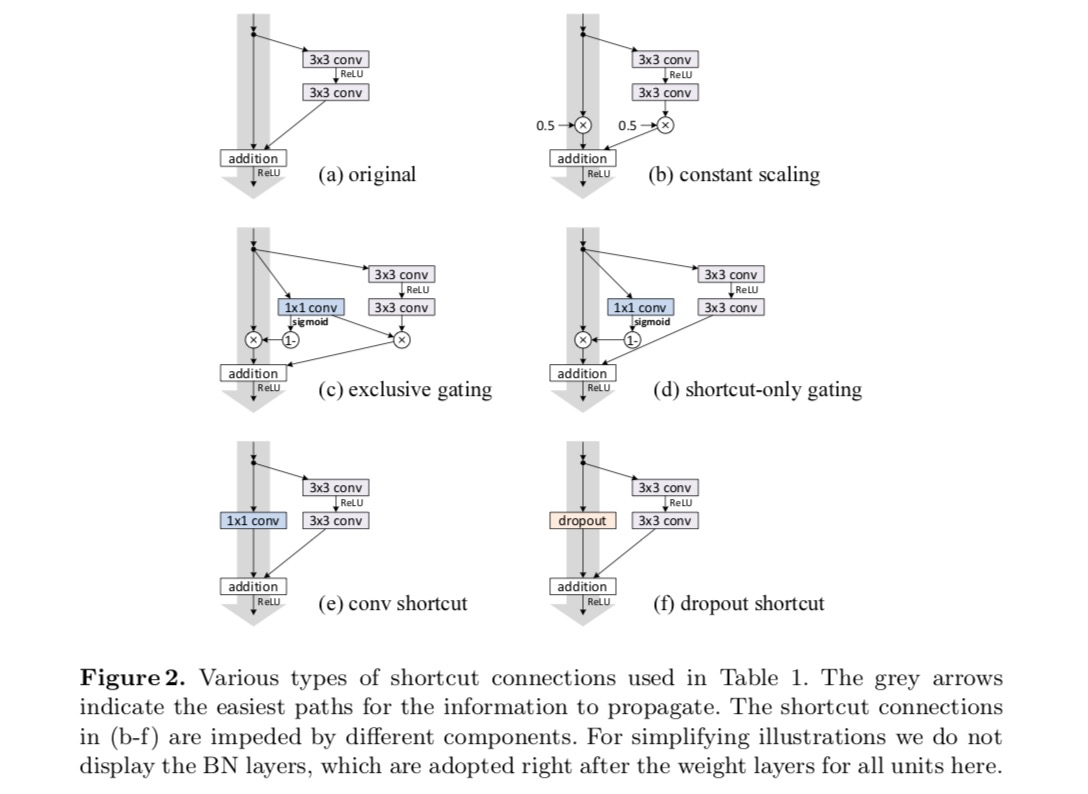
wyniki klasyfikacji są wyświetlane w poniższej tabeli:

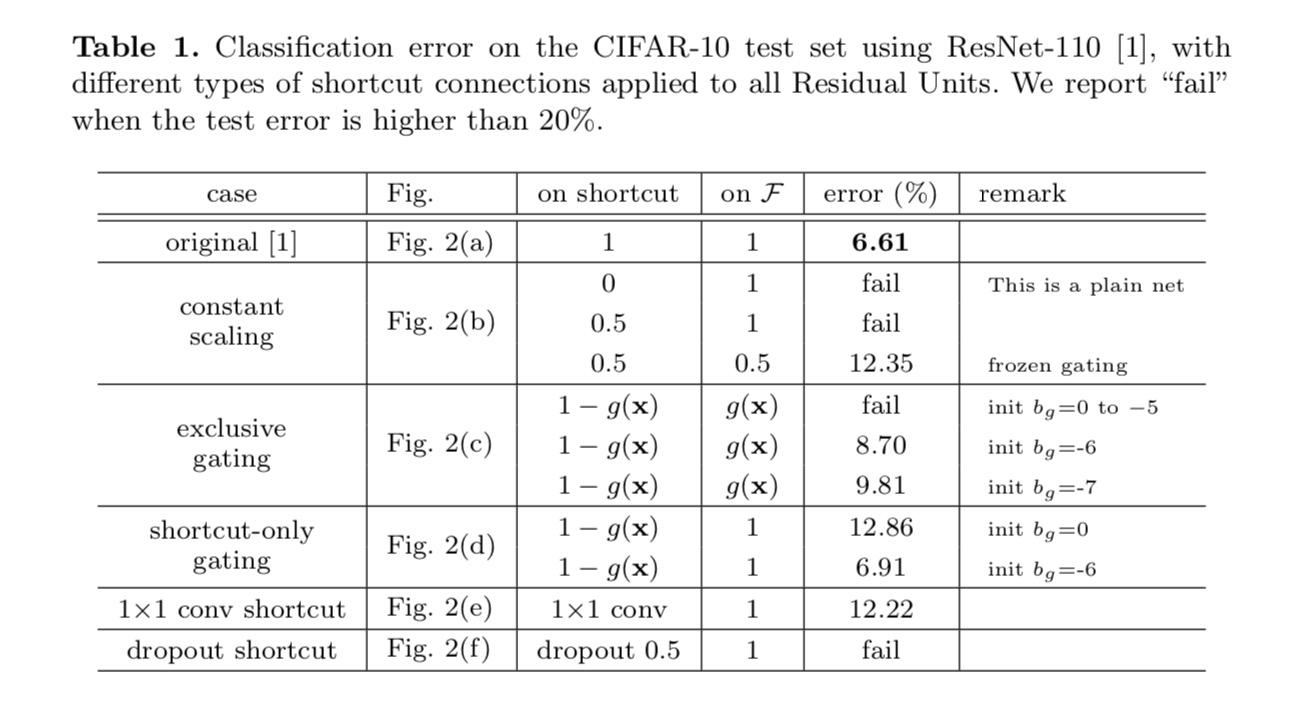
jak wskazują szare strzałki na powyższym rysunku, połączenia skrótów są najbardziej bezpośrednimi ścieżkami propagacji informacji. Manipulacje multiplikatywne (skalowanie, bramkowanie, sploty 1×1 i porzucenie) na skrótach mogą utrudniać propagację informacji i prowadzić do problemów optymalizacyjnych.

warto zauważyć, że skróty gating i 1×1 convolutional wprowadzają więcej parametrów i powinny mieć silniejsze zdolności reprezentacyjne niż skróty tożsamościowe. W rzeczywistości bramkowanie tylko na skróty i splot 1×1 obejmują przestrzeń rozwiązania skrótów tożsamości (tzn. można je zoptymalizować jako skróty tożsamości). Jednak ich błąd treningowy jest wyższy niż w przypadku skrótów tożsamościowych, co wskazuje, że degradacja tych modeli jest spowodowana problemami optymalizacyjnymi, a nie zdolnościami reprezentacyjnymi.

wykorzystanie funkcji aktywacyjnych

eksperymenty w powyższej sekcji zakładają, że aktywacja po dodaniu jest odwzorowaniem tożsamości. Ale w powyższych eksperymentach jest ReLU, jak zaprojektowano w pierwszym artykule. Następnie badamy wpływ .

chcemy wykonać mapowanie tożsamości, które odbywa się poprzez ponowne uporządkowanie funkcji aktywacyjnych (ReLU i/lub BN, normalizacja wsadowa). Na poniższym rysunku oryginalna Jednostka resztkowa w ostatnim papierze ma kształt na Fig. 4 (a) – BN stosuje się po każdej warstwie wagowej, a ReLU przyjmuje się po BN, z tym że ostatni ReLU w jednostce resztkowej jest po dodaniu pierwiastkowym (=ReLU). Fig. 4 (b-e) Pokaż alternatywy, które zbadaliśmy.

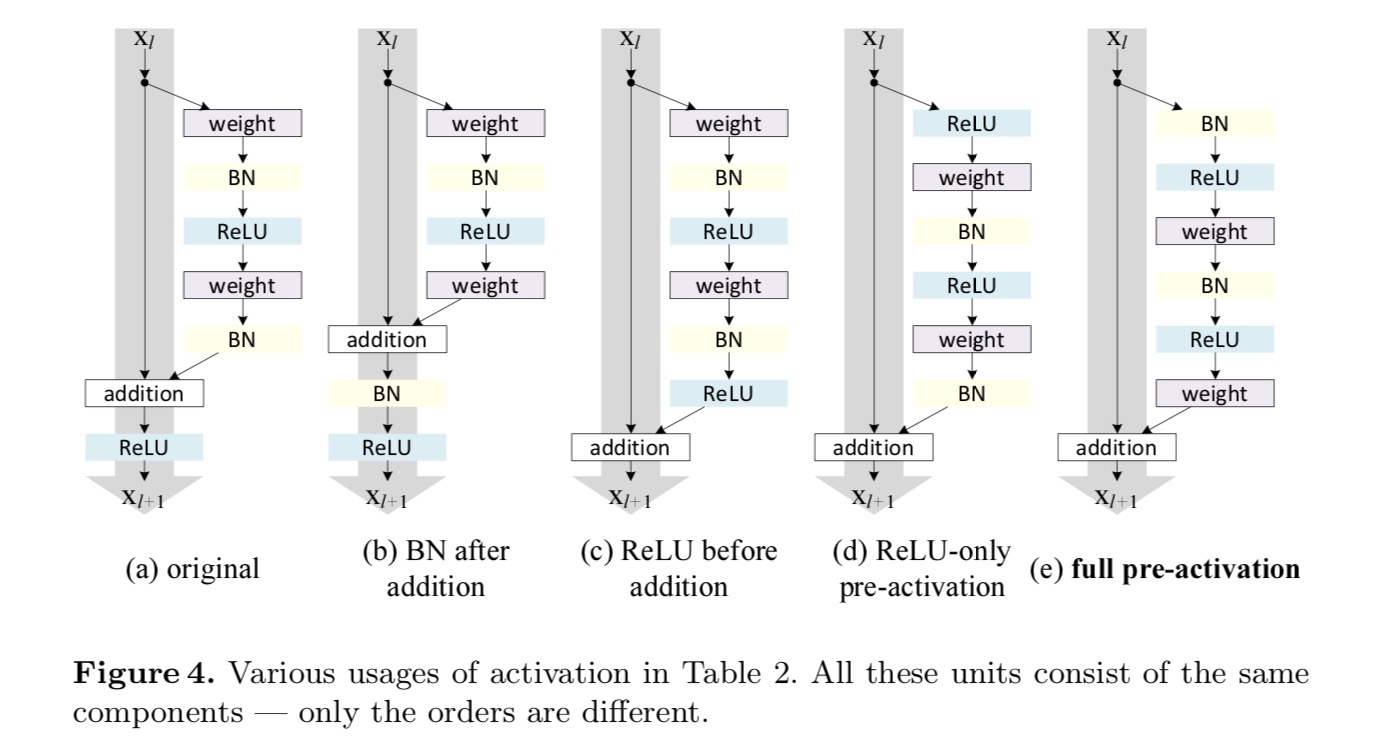
eksperymenty z aktywacją

w tej sekcji eksperymentujemy z ResNet-110 i 164-warstwową architekturą wąskich gardeł (oznaczoną jako ResNet-164). Jednostka resztkowa wąskiego gardła składa się z warstwy 1×1 dla zmniejszenia wymiaru, warstwy 3×3 i warstwy 1×1 dla przywrócenia wymiaru. Jak zaprojektowano w ostatnim artykule, jego złożoność obliczeniowa jest podobna do jednostki rezydualnej dwu-3×3.

Po aktywacji czy przed aktywacją?

w oryginalnym projekcie aktywacja wpływa na obie ścieżki w następnej jednostce resztkowej: . Następnie rozwijamy formę asymetryczną, w której aktywacja wpływa tylko na ścieżkę:, for any . Zmieniając nazwy notacji, mamy następującą postać:

dla tej nowej jednostki resztkowej, tak jak w powyższym równaniu, Nowa aktywacja po dodaniu staje się mapowaniem tożsamości. Taka konstrukcja oznacza, że jeśli nowa aktywacja po dodaniu jest asymetrycznie przyjęta, jest ona równoważna przekształceniu jako aktywacja wstępna następnej jednostki resztkowej. Jest to zilustrowane na poniższym rysunku:

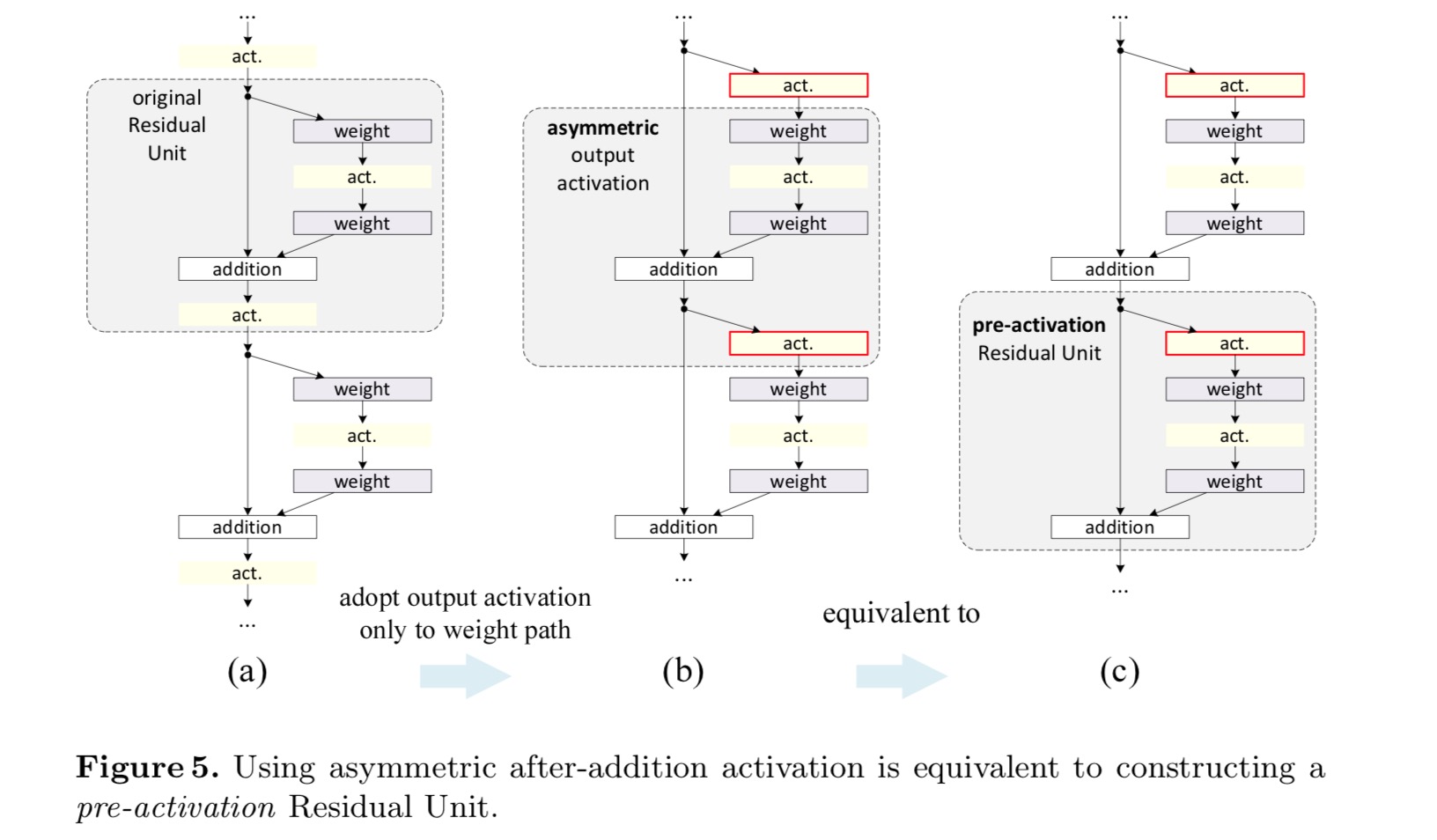
rozróżnienie między Po aktywacji / przed aktywacją jest spowodowane obecnością dodawania pierwiastków. Dla zwykłej sieci, która ma N warstw, istnieje aktywacja N-1 (BN/ReLU) i nie ma znaczenia, czy myślimy o nich jako o aktywacjach po – czy pre -. Ale dla rozgałęzionych warstw połączonych przez dodanie, pozycja aktywacji ma znaczenie. Różne zastosowania aktywacji są pokazane na rysunku 4.

eksperymentujemy z dwoma takimi projektami: (1) aktywacja wstępna tylko dla ReLU i (2) pełna aktywacja wstępna, w przypadku gdy BN i ReLU są przyjmowane przed warstwami wagowymi. Jakoś zaskakująco, gdy BN i ReLU są używane jako pre-aktywacja, wyniki są poprawiane przez zdrowe marginesy

uważamy, że wpływ pre-aktywacji jest dwojaki. Po pierwsze, optymalizacja jest jeszcze łatwiejsza (w porównaniu z bazowym Resnetem), ponieważ F jest mapowaniem tożsamości. Po drugie, zastosowanie BN jako aktywacji wstępnej poprawia regularyzację modeli.

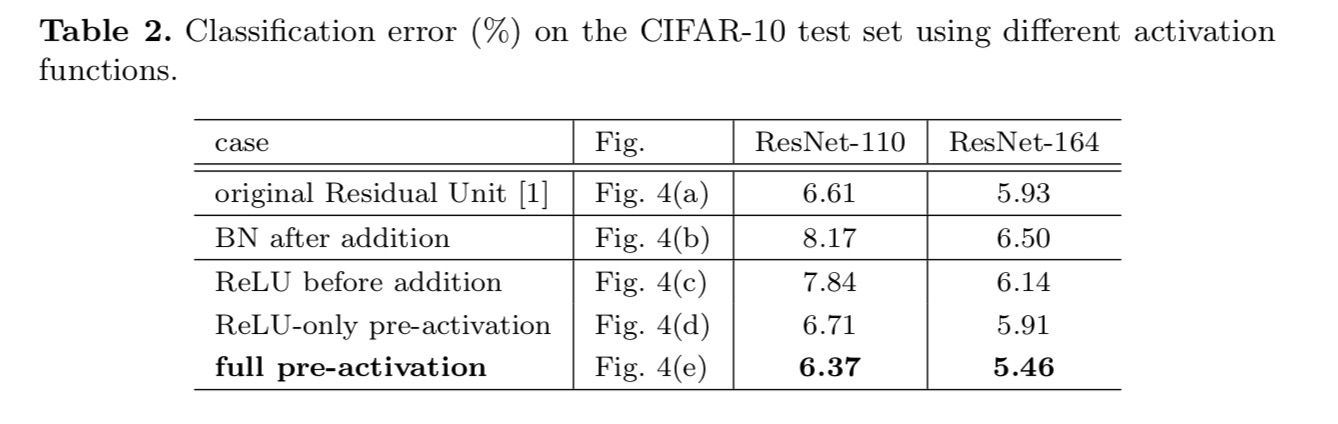
wnioski

niniejsza praca bada sposoby propagacji mechanizmów połączeń głębokich sieci szczątkowych. Nasze wyprowadzenia sugerują, że skrócenie tożsamości i aktywacja tożsamości po dodaniu są niezbędne do sprawnego propagowania informacji. Eksperymenty ablacyjne wykazują phenom-ena, które są zgodne z naszymi pochodnymi. Prezentujemy również 1000-warstwowe sieci Głębokie, które można łatwo wyszkolić i osiągnąć lepszą dokładność.

zagregowana transformacja szczątkowa dla głębokich sieci neuronowych

wprowadzenie

badania nad rozpoznawaniem wizualnym przechodzą z „inżynierii funkcji” do „inżynierii sieci”. Wysiłek ludzki został przesunięty na projektowanie lepszych architektur sieci do uczenia się reprezentacji.

projektowanie architektur staje się coraz trudniejsze z rosnącą liczbą hiper-parametrów, zwłaszcza gdy istnieje wiele warstw. Sieci VGG wykazują prostą, ale skuteczną strategię budowy bardzo głębokich sieci: układania bloków konstrukcyjnych o tym samym kształcie. Strategia ta jest dziedziczona przez Resnety, które układają moduły o tej samej topologii. Ta prosta zasada zmniejsza swobodę wyboru hiper parametrów, a głębokość jest eksponowana jako podstawowy wymiar w sieciach neuronowych. Ponadto argumentujemy, że prostota tej reguły może zmniejszyć ryzyko nadmiernego dostosowania hiperparametrów do określonego zbioru danych. Wytrzymałość sieci VGG i Resnetów została udowodniona przez różne zadania rozpoznawania wizualnego i zadania niewizualne obejmujące mowę i język.

w przeciwieństwie do sieci VGG, rodzina modeli Incepcyjnych wykazała, że starannie zaprojektowane topologie są w stanie osiągnąć przekonującą Dokładność przy niskiej złożoności teoretycznej. Modele Incepcji ewoluowały z czasem, ale ważną wspólną cechą jest strategia split-transform-merge. W module Incepcji wejście jest dzielone na kilka dolnych wymiarów osadzeń (przez 1×1 sploty), przekształcanych przez zestaw specjalistycznych filtrów (3×3, 5×5 itp.) i połączone przez konkatenację. Oczekuje się, że zachowanie split-transform-merge modułów Incepcyjnych zbliży się do siły reprezentacyjnej dużych i gęstych warstw, ale przy znacznie niższej złożoności obliczeniowej.

pomimo dobrej dokładności, realizacji modeli Incepcji towarzyszył szereg czynników komplikujących. Chociaż ostrożne kombinacje tych komponentów dają doskonałe receptury sieci neuronowych, ogólnie nie jest jasne, jak dostosować architektury Incepcji do nowych zbiorów danych/zadań, zwłaszcza gdy istnieje wiele czynników i hiper-parametrów do zaprojektowania.

w niniejszym artykule przedstawiamy prostą architekturę, która przyjmuje strategię VGG/ResNets polegającą na powtarzaniu warstw, jednocześnie wykorzystując strategię split-transform-merge w łatwy, rozszerzalny sposób. Moduł w naszej sieci wykonuje zestaw przekształceń, każda na niskowymiarowym osadzeniu, których wyniki są agregowane przez sumowanie. Dążymy do prostej realizacji tej idei — transformacje, które mają być zagregowane, mają tę samą topologię. Ta konstrukcja pozwala nam rozszerzyć na dowolną dużą liczbę przekształceń bez specjalistycznych projektów.

empirycznie wykazujemy, że nasze zagregowane transformacje przewyższają pierwotny moduł ResNet, nawet pod ograniczonym warunkiem zachowania złożoności obliczeniowej i rozmiaru modelu. Podkreślamy, że chociaż stosunkowo łatwo jest zwiększyć dokładność poprzez zwiększenie pojemności (sięganie głębiej lub szerzej), metody zwiększające Dokładność przy zachowaniu (lub zmniejszeniu) złożoności są rzadkie w literaturze.

nasza metoda wskazuje, że Kardynalność (wielkość zbioru przekształceń) jest konkretnym, mierzalnym wymiarem, który oprócz wymiarów szerokości i głębokości ma centralne znaczenie. Eksperymenty pokazują, że zwiększenie cardinality jest bardziej skutecznym sposobem na uzyskanie dokładności niż wchodzenie głębiej lub szerzej, zwłaszcza gdy głębokość i szerokość zaczynają dawać malejące zwroty dla istniejących modeli.

nasze sieci neuronowe, nazwane ResNeXt (sugerując następny wymiar), przewyższają ResNet-101/152, ResNet-200, Inception-v3 i Inception-ResNet-v2 w zestawie danych klasyfikacji ImageNet. W szczególności 101-warstwowy ResNeXt jest w stanie osiągnąć lepszą dokładność niż ResNet-200, ale ma tylko 50% złożoności. Ponadto ResNeXt wykazuje znacznie prostsze konstrukcje niż wszystkie modele Incepcji.

metoda

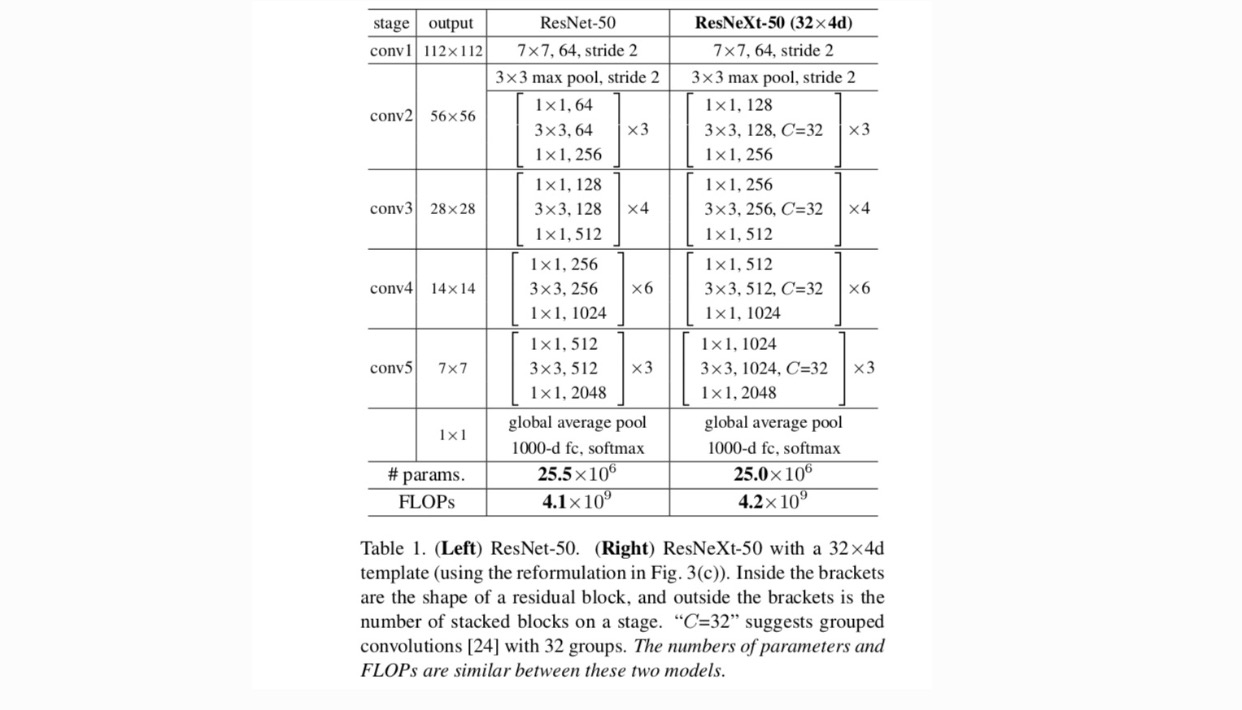
przyjmujemy wysoce modularny projekt po VGG/ResNets. Nasza sieć składa się ze stosu pozostałych bloków. Bloki te mają tę samą topologię i podlegają dwóm prostym zasadom zainspirowanym przez VGG / ResNets: (1) w przypadku tworzenia map przestrzennych tego samego rozmiaru, bloki mają te same hiper-parametry (szerokość i rozmiary filtrów), oraz (2) za każdym razem, gdy mapa przestrzenna jest zmniejszana o współczynnik 2, Szerokość bloków jest mnożona przez współczynnik 2. Druga zasada zapewnia, że złożoność obliczeniowa, w kategoriach FLOPs (operacje zmiennoprzecinkowe, w #mnożenie-dodaje), jest w przybliżeniu taka sama dla wszystkich bloków.

dzięki tym dwóm zasadom wystarczy zaprojektować moduł szablonu, a wszystkie moduły w sieci można odpowiednio określić. Te dwie zasady znacznie zawężają przestrzeń projektową i pozwalają nam skupić się na kilku kluczowych czynnikach. Sieci skonstruowane na podstawie tych zasad przedstawiono w tabeli 1.

najprostsze neurony w sztucznych sieciach neuronowych wykonują produkt wewnętrzny (sumę ważoną), czyli elementarną transformację wykonywaną przez w pełni połączone i splątane warstwy.

powyższą operację można przekształcić jako kombinację dzielenia, przekształcania i agregowania. (1): dzielenie: wektor jest krojony jako nisko-wymiarowe osadzenie, aw powyższym, jest to podprzestrzeń jednowymiarowa (2) przekształcanie: reprezentacja niskowymiarowa jest przekształcana, aw powyższym, jest po prostu skalowana: (3) agregowanie: transformacje we wszystkich osadzeniach są agregowane przez .

biorąc pod uwagę powyższą analizę prostego neuronu, rozważamy zastąpienie elementarnej transformacji (w_i, x_i) bardziej ogólną funkcją, która sama w sobie może być również siecią. Formalnie transformacje sumaryczne prezentujemy jako:

gdzie może być funkcją dowolną. Analogiczny do prostego neuronu, powinien rzutować na (opcjonalnie niskowymiarowe) osadzenie, a następnie przekształcić je.

nazywamy to kardynalnością. jest w pozycji podobnej do in, ale nie musi być równa i może być dowolną liczbą. Eksperymentami pokazujemy, że Kardynalność jest istotnym wymiarem i może być bardziej efektywna niż wymiary szerokości i głębokości.

w tym artykule rozważamy prosty sposób projektowania funkcji transformacji: wszystkie mają tę samą topologię. Rozszerza to strategię w stylu VGG polegającą na powtarzaniu warstw o tym samym kształcie. Indywidualną transformację ustawiamy jako architekturę w kształcie wąskiego gardła, pokazaną na Rys. 1 (po prawej). W tym przypadku pierwsza warstwa 1×1 w każdej tworzy niskowymiarowe osadzenie.

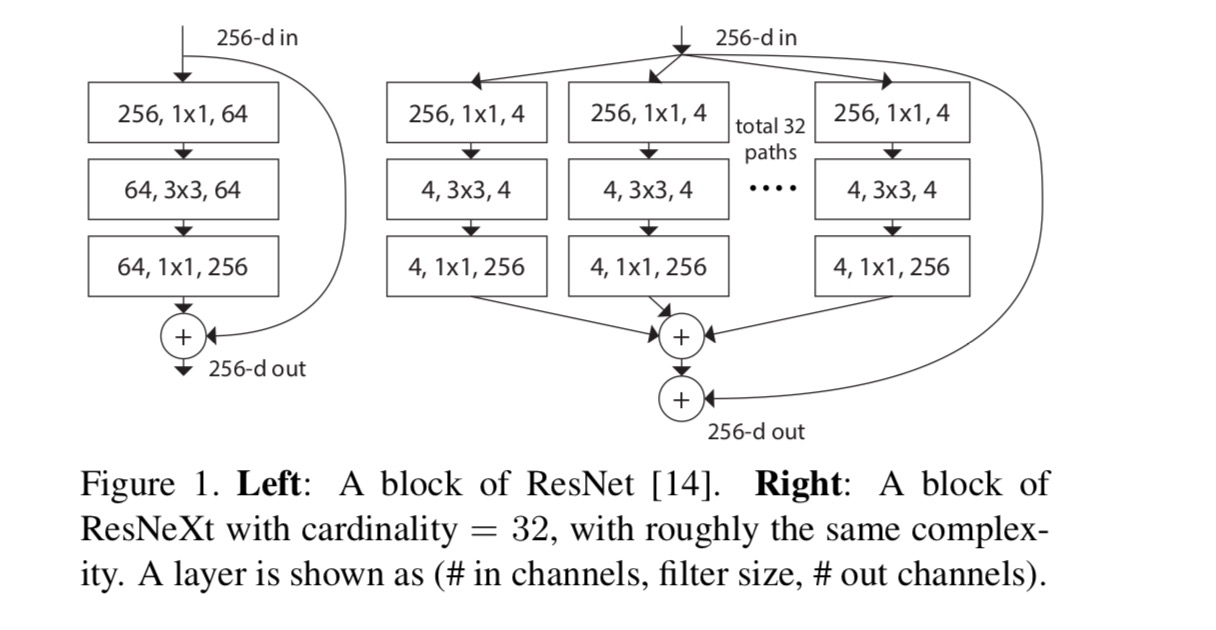
zagregowane przekształcenie w ostatnim równaniu służy jako funkcja rezydualna:

Gdzie jest wyjście.

relacje pomiędzy ResNeXt i Inception-ResNet / Grouped-Convolutions są pokazane na poniższym rysunku:

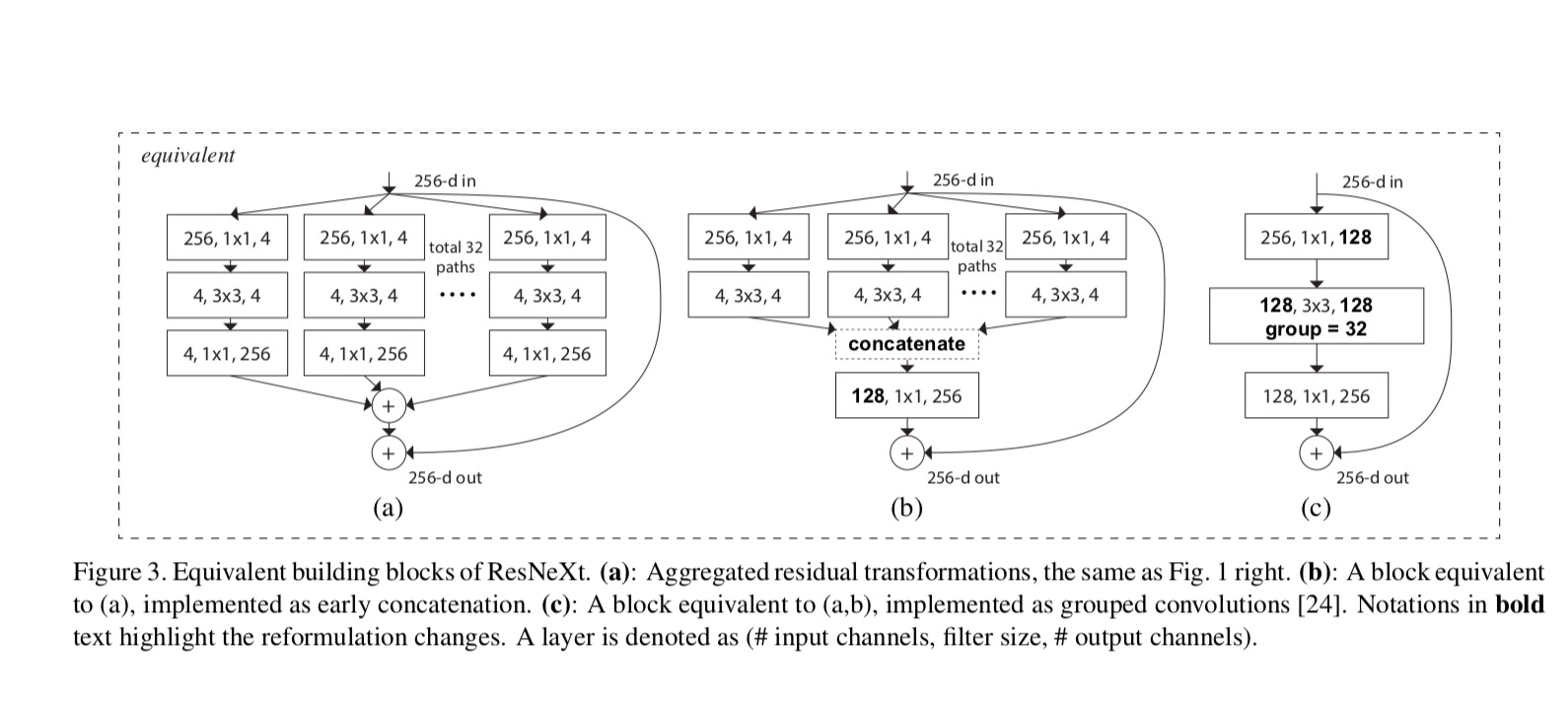
gdy oceniamy różne kardynalności przy zachowaniu złożoności, chcemy zminimalizować modyfikację innych hiper-parametrów. Wybieramy dopasowanie szerokości wąskiego gardła(np. 4-d na Rys. 1 (po prawej)), ponieważ można go odizolować od wejścia i wyjścia bloku. Strategia ta nie wprowadza zmian do innych hyper-parametrów (głębokość lub szerokość wejścia/wyjścia bloków), więc jest pomocne dla nas, aby skupić się na wpływ cardinality.

na Rys. 1 (po lewej), oryginalny blok wąskich gardeł ResNet ma parametry i proporcjonalne Flopy (na tym samym rozmiarze mapy funkcji). Z wąskim gardłem szerokości, nasz szablon na Rys. 1 (po prawej) ma: parametry i proporcjonalne Flopy. Kiedy i, ten numer . Poniższa tabela przedstawia zależność między cardinalnością a wąskim gardłem szerokości .

Najpierw oceniamy kompromis między cardinalnością a wąskim gardłem, w ramach zachowanej złożoności, zgodnie z tabelą 2. Tabela 3 przedstawia wyniki. W porównaniu z ResNet-50, ResNeXt-50 32×4D ma błąd walidacji wynoszący 22,2%, czyli o 1,7% niższy od bazowego Resnetu 23,9%. Wraz ze wzrostem liczby kardynalnej z 1 do 32 przy zachowaniu złożoności, współczynnik błędów stale się zmniejsza. Ponadto ResNeXt 32×4D ma również znacznie niższy błąd treningowy niż ResNet countetpart, co sugeruje, że zyski nie wynikają z regularyzacji, ale z silniejszych reprezentacji.

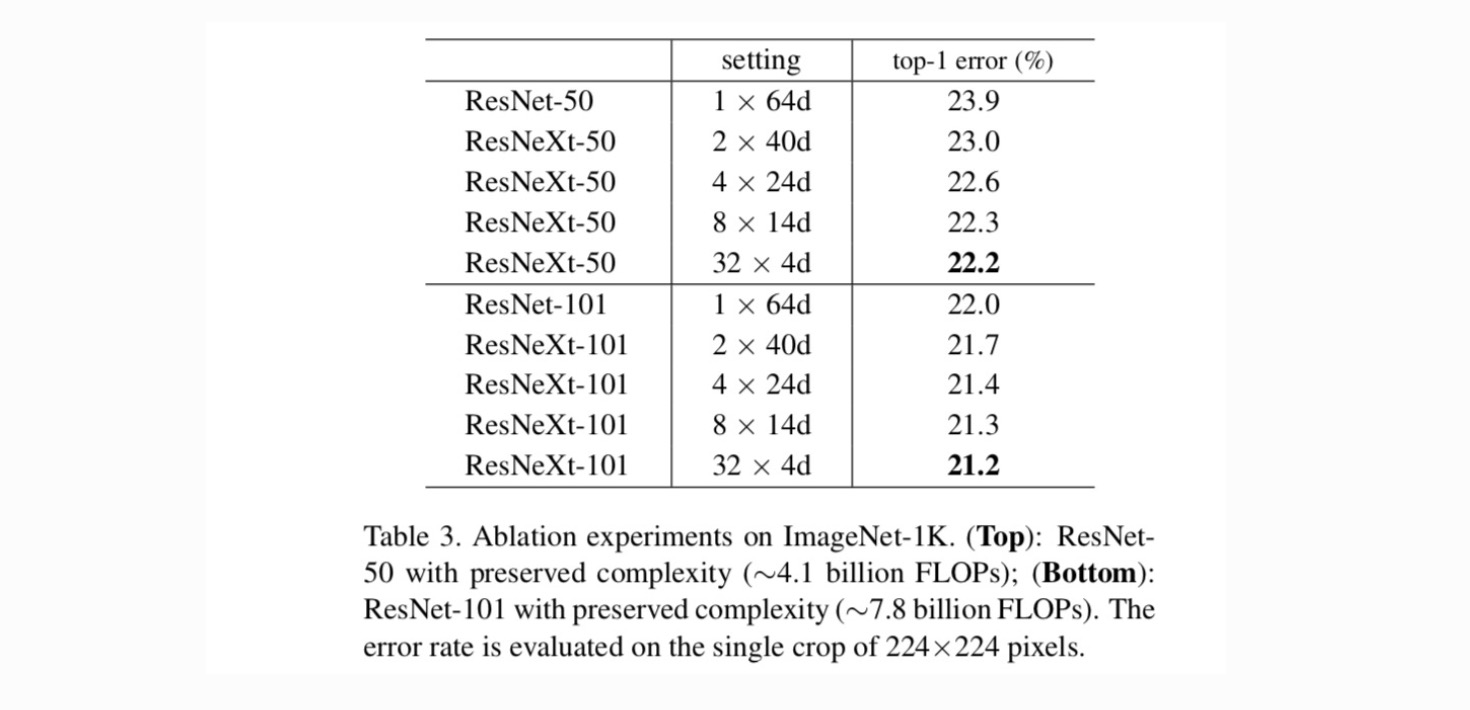
następnie badamy rosnącą złożoność poprzez zwiększenie cardinality C lub zwiększenie głębokości lub szerokości. Porównujemy następujące warianty (1) idąc głębiej do 200 warstw. Przyjmujemy ResNet-200. (2) zwiększenie szerokości wąskiego gardła. (3) zwiększenie cardinalności poprzez podwojenie C.

Tabela 4 pokazuje, że zwiększenie złożoności o 2× konsekwentnie zmniejsza błąd w stosunku do linii bazowej ResNet-101 (22,0%). Ale poprawa jest niewielka, gdy idzie się głębiej (ResNet-200, o 0,3%) lub szerzej (szerszy ResNet-101, o 0,7%). Wręcz przeciwnie, zwiększenie cardinality C pokazuje znacznie lepsze wyniki niż wchodzenie głębiej lub szerzej.

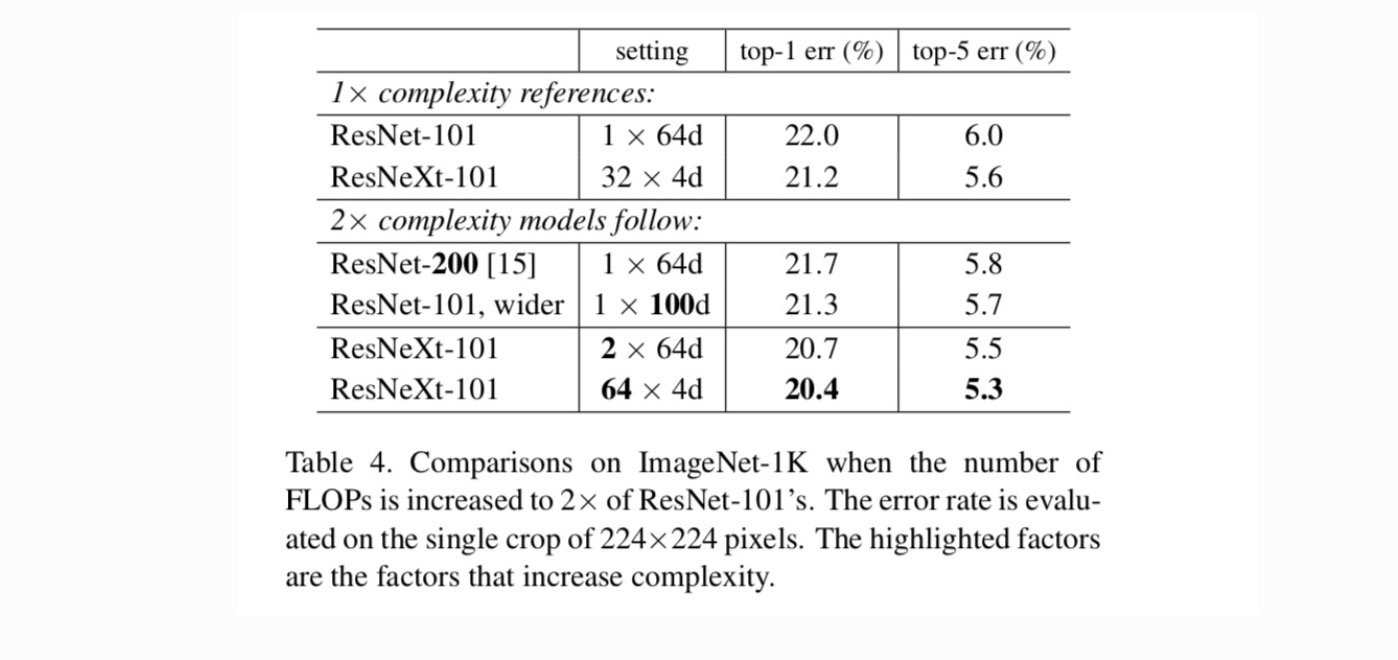
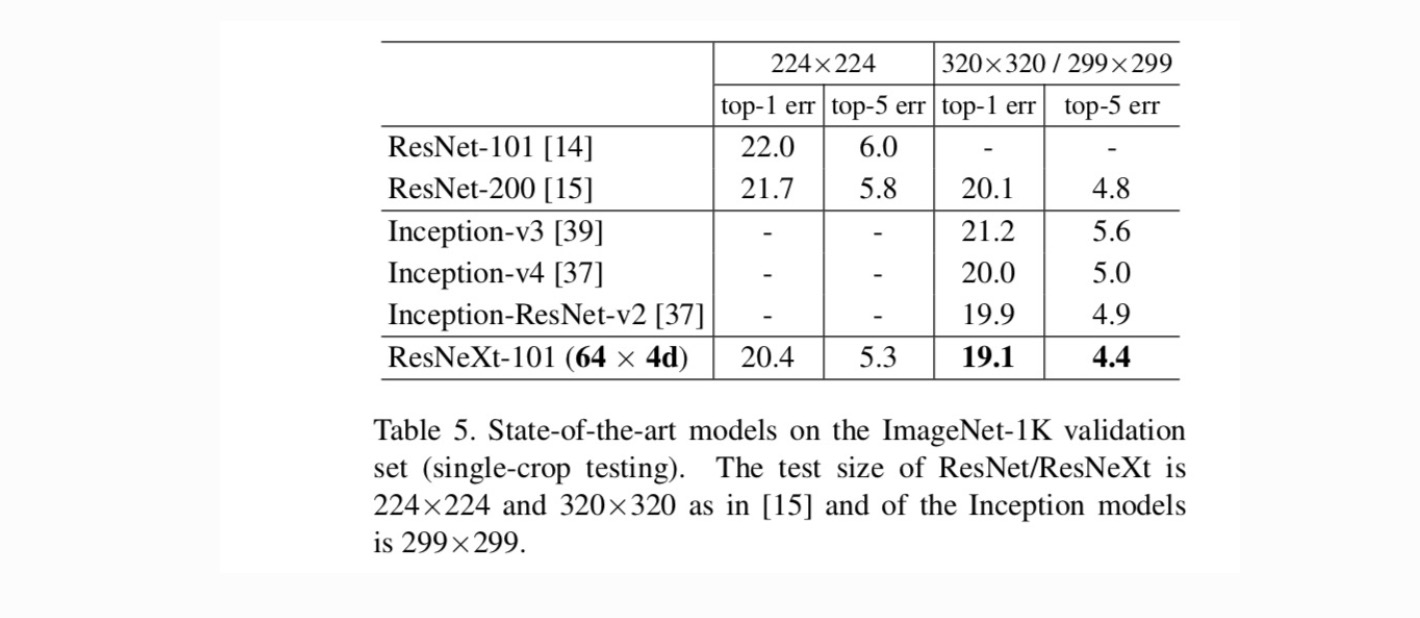
Tabela 5 pokazuje więcej wyników testów pojedynczych upraw w zestawie walidacji ImageNet. Nasze wyniki porównują się korzystnie z ResNet, Inception-V3 / v4 i Inception-ResNet-v2, osiągając wskaźnik błędu single-Crop top-5 na poziomie 4,4%. Ponadto nasz projekt architektoniczny jest znacznie prostszy niż wszystkie modele Incepcji i wymaga znacznie mniejszej liczby hiperparametrów do ręcznego ustawiania.